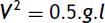Mechanical stiffness: a global parameter associated to elite sprinters performance

Rigidez mecânica: um parâmetro global associado com desempenho em velocistas de elite

Rigidez mecánica: un parámetro global asociado con el rendimiento en velocistas de élite

Abstract

This study analyzes vertical stiffness as a global parameter that could be directly associated to sprinter's performance. We evaluated vertical stiffness, performance, heart rate and lactate concentration on fifteen male sprinters that ran on a treadmill at gait transition speed and 13 km h⁻¹. Vertical Stiffness was determined by the ratio of the vertical acceleration peak and maximum displacement of the center of mass. Physiological parameters were measured throughout the experimental procedure and performance was estimated by athlete's time records on 100 m track race. As expected, vertical stiffness and heart rate increased with running speed. We found a high correlation between heart rate and vertical stiffness at gait transition speed. However, at 13 km h⁻¹, lactate peak showed a higher correlation with vertical stiffness, suggesting a greater participation of the anaerobic system. An inverse relationship between performance and vertical stiffness was found, where faster athletes were the stiffer ones. Performance and lactate peak presented the same inverse relationship; faster athletes had higher lactate peaks. As a result, faster athletes were stiffer and consume more energy. All in all, these findings suggest that mechanical stiffness could be a potential global parameter to evaluate performance in sprinters.

KEYWORDS Stiffness; Sprint; Biomechanics; Performance

Resumo

Este estudo analisa a rigidez vertical como um parâmetro global que poderia ser diretamente associado ao desempenho em velocistas. Avaliou-se a rigidez vertical, o desempenho, a frequência cardíaca e a concentração de lactato em 15 velocistas do sexo masculino, todos altamente treinados, que correram em uma esteira à velocidade de transição e a 13 km.h⁻¹. A rigidez vertical foi determinada pela razão entre o pico de aceleração vertical e o deslocamento máximo do centro de massa. Os parâmetros fisiológicos foram mesurados na coleta de dados e o desempenho foi estimado por registros de tempo em 100 metros de corrida. Como esperado, a rigidez vertical e a frequência cardíaca aumentaram com a velocidade. A rigidez e a frequência cardíaca obtiveram alta correlação na menor velocidade. Contudo, a 13 km.h⁻¹ o pico de lactato mostrou alta correlação com a rigidez, o que sugere uma maior participação do sistema anaeróbico. Uma relação inversa foi achada entre rigidez e registros de tempo, nos quais os atletas mais rápidos são os mais rígidos. Além disso, os atletas mais rápidos foram os que apresentaram os maiores picos de lactato. Assim, este estudo sugere que a rigidez vertical poderia ser um parâmetro global para avaliar o desempenho dos velocistas.

PALAVRAS-CHAVE Rigidez; Corrida de velocidade; Biomecânica; Desempenho físico

Resumen

Este estudio analiza la rigidez vertical como un parámetro global que podría estar directamente relacionado con el rendimiento en velocistas. Se evaluó la rigidez vertical, el rendimiento, la frecuencia cardíaca y la concentración de lactato en 15 velocistas de sexo masculino, muy entrenados, que corrieron en una cinta a la velocidad de transición y a 13 km/h⁻¹. La rigidez vertical se calculó por el cociente entre el pico de aceleración vertical y el desplazamiento máximo del centro de masa. Los parámetros fisiológicos se midieron durante el procedimiento experimental y el rendimiento se estimó a través del tiempo de cada atleta en 100 m llanos. Como era de esperar, la rigidez vertical y la frecuencia cardíaca aumentaron con la velocidad. Se encontró una alta correlación entre frecuencia cardíaca y rigidez vertical a la velocidad más baja. Sin embargo, a 13 km/h⁻¹, el pico de lactato mostró una alta correlación con la rigidez vertical, lo que sugería mayor participación del sistema anaeróbico. Se encontró una relación inversa entre el rendimiento y la rigidez vertical, donde los atletas más rápidos fueron más rígidos. Asimismo, el rendimiento y el pico de lactato presentaron la misma relación inversa; los atletas más rápidos mostraron los picos más altos de lactato. Por consiguiente, los atletas más rápidos fueron más rígidos y consumieron más energía. Estos resultados sugieren que la rigidez mecánica podría ser un parámetro global para evaluar el rendimiento de los velocistas.

PALABRAS CLAVE Rigidez; Sprint; Biomecánica; Rendimiento

Introduction

A running sprinter coordinates the actions of many muscles, tendons, and ligaments in its leg so that the overall leg behaves like a single mechanical spring during ground contact (Farley et al., 1993). In fact, the simplest model of a running sprinter is a spring-mass system consisting of a linear spring representing the stance limb and a point mass equivalent to body mass (Blickhan, 1989; Mcmahon and Cheng, 1990). During support, vertical force component is acting on the spring and thus mechanical stiffness can be calculated from the ratio of this force to the change in spring length.

The spring mass model has been used in optimization studies (Alexander, 2003) and to test hypothesis that are directly related to sport and training fields (Morin et al., 2011; Di Michele et al., 2012). The reasons for using this model in these areas are mainly its simplicity and globality since evaluations generally have the tendency to analyze one or a few parameters only.

Assuming the spring mass model, previous studies have used different methods and equipments for estimating mechanical stiffness when running (Brughelli and Cronin, 2008). One of the approaches most commonly used is vertical stiffness (K_vert) (Mcmahon et al., 1987; Cavagna et al., 1988; Morin et al., 2005, 2011; Di Michele et al., 2012). This parameter relates to the peak vertical force and the vertical motion of the center of mass during the contact with the ground (Brughelli and Cronin, 2008). Both, the force peak and the displacement of the center of mass depend on muscular activation, fiber type and muscular volume (Herzog, 2000) and is thought to influence several athletic variables, including rate of force development, storage of elastic energy, stride frequency, ground contact time and sprint kinematics (Farley and Gonzalez, 1996; Mcmahon and Cheng, 1990). In this way, changes in K_vert could influence sprinter's performance when running and its quantification could provide a useful tool to evaluate sprinters.

It is widely known that strength is a major quality for athletes to develop, thus it is closely associated to running speed. All elite sprinters have a common feature; huge lean muscles with high percentage of explosive fibers that are intensively activated when racing (Kubo et al., 2011). During each step phase, athletes perform maximum force in a very short period of time, recruiting high percentage of muscle fibers and activating contractile elements to generate intensive stretch-shortening cycles in a coordinated manner (Nigg et al., 2000). Therefore, maximum power is perform during ground contact, increasing speed and improving time records.

Having a larger muscular volume, build up by fast and explosive fibers, with a larger cross section than slow fibers and a high percentage of activated fibers, could determine an increase in force peak during ground contact phase leading to an increase in K_vert.

Nonetheless, an athlete with a larger muscular volume and a high percentage of activated fibers would consume more energy. K_vert depends directly on the force peak and this on muscle characteristics that would determind energy consumption. Energy consumption during exercise can be estimated throughout different physiological parameters such as heart rate and blood lactate concentration. The analysis of these parameters would provide further insight on K_vert values considering them as a real feedback of physiological processes happening inside muscle tendon unit of the limbs.

The aim of this study is to provide a better understanding on the importance of mechanical stiffness as a global parameter that could be directly associated to athlete's performance.

Our hypothesis is that athletes with higher mechanical stiffness will consume more energy and will have faster time records in 100 m.

For that purpose, we analyzed K_vert of elite sprinters through a 3D filming and reconstruction procedure at controlled conditions and lactate concentration and heart rate to assay their relationship with athlete's performance. If the hypothesis is correct, the physiological and mechanical parameters studied here should follow the same trend of change and have a high correlation with athlete's time records. As a result, mechanical stiffness could be a potential global parameter to predict performance in sprinters.

Methods

Experimental approach to the problem

The study design is composed by the analysis of three different variables.

By using a three dimensional filming method (cinemetry), athlete's mechanical stiffness (K_vert) was assayed. This method, based on the spring-mass model, provides insights on the motion of the center of mass when running. Secondly, physiological parameters such as lactate peak and heart rate were measured to analyze energy consumption. These can be considering as a real feedback of the physiological processes happening inside muscle tendon units of the limbs.

Finally, we measured athlete's performance by their time records in 100 m track race. Time records were measured under controlled conditions (same day, track, distance, wind speed and chronometer) for all sprinters.

With these information, we tested our hypotheses to provide a better understanding on the importance of K_vert as a global parameter that could be directly associated to athlete's performance.

Subjects

A sample of fifteen male athletes, all highly trained sprinters (19.7 ± 1.28 years, 69.50 ± 2.68 kg) voluntarily participated in this study. The sample was conveniently selected among athletes with the best time records in 100 m in the country.

The sample size (n) was estimated throughout a comparison model:

where n = number of athletes, Z_a and Z_b = risk values, S² = variance of K_vert (taken from bibliography) and d = minimum difference detected when comparing two K_vert values at different speeds. Also, we considered unilaerality and set α = 0.05 and β = 0.05.

The exclusion criteria considered were the presence of any injury within the last 6 month or if the training period was different from pre-competition/competition. Once the sample was selected, none of the individuals had to be excluded from the trial.

This study complied with the requirements of the local Committee for Medical Research Ethics and current Uruguayan law and regulations. The participants were informed about the objectives and characteristics of the study, and their consent was obtained.

Procedures

Performance was measured by athlete's time records on 100 m track race. Athletes were requested to race a 100 m on an official trail in the National Athletic Stadium. Time records were measured under controlled conditions (same day, track, distance, wind speed and chronometer) for all sprinters.

After evaluating performance, athletes were taken to the Laboratory of Movement in the Hospital de Clínicas to evaluate K_vert and physiological parameters.

Athletes were dressed up in black tight clothes and covered with 18 white markers in different anatomical landmarks to identify them for subsequent digitalization. The selected points were the fifth metatarsal, lateral malleolus, femoral condyle, greater trochanter, acromion, sphenoid, lateral epicondyle of the humerus, radial styloid process and head of the third metacarpal. Prior to performing the experimental procedures, two anthropometric variables were measured: body mass and leg length (trochanteric height measured from the greater trochanter to the floor).

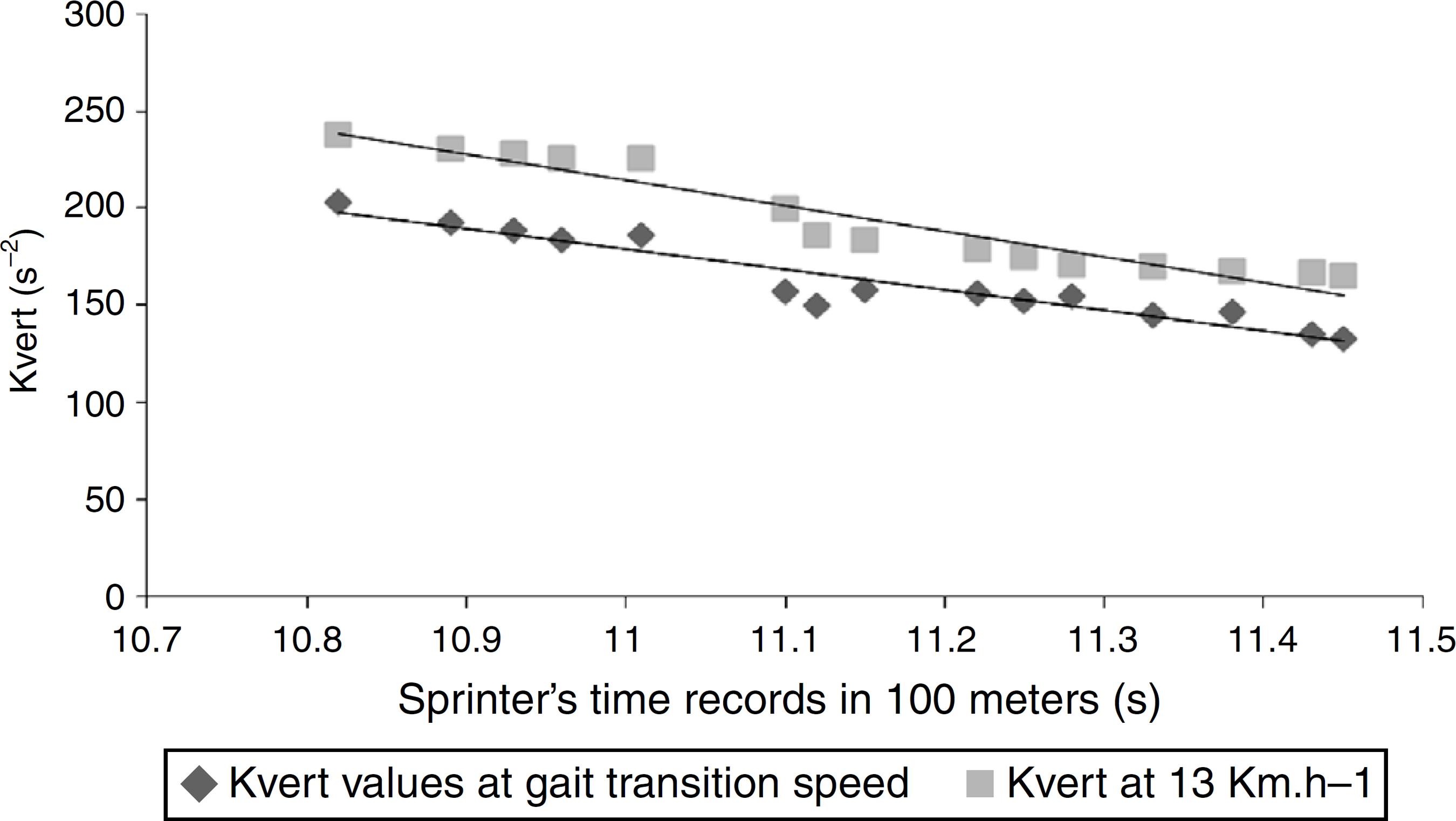
Each subject ran on a treadmill for 10 min at two different speeds. We used two different running speeds to confirm that K _vert and physiological parameters vary with changes in velocity (Arampatzis and Metzle, 1999). During the first 5 min, athletes ran at their gait transition speed established by Freud's equation:

where V is the running speed, 0.5 is Freud's number for gait transition speed, g is acceleration due to gravity (9.8 m s⁻² on earth) and l is the leg length in meters (Saibene and Minetti, 2003). The remaining 5 min athletes ran at 13 km h⁻¹, speed at which muscles work mainly in isometric contraction (Fisher, 2010). We selected these running speeds since the model we are using to calculate K _vert perfectly adjusts and is valid at low running velocities. In this way, although we are not measuring K _vert at the usual high speed of a race, this parameter calculated at low speeds reflects the global mechanic characteristics of the athlete (Cavagna et al., 1988).

Images were recorded with 4 synchronized DCR-H28E digital video cameras, these were placed on 950 ALS UNOMAT tripods following a 90 degree angle layout within each other to ensure that athlete's sagital plane was captured by two cameras (Fig. 1). In this way, a three-dimensional reconstruction was performed to determine the position of athlete's center of mass (CM) and calculate the mechanical stiffness throughout K_vert.

Figure 1
Schematic layout of the cameras placed round the treadmill. The arrow indicates movement direction.

Once the filming process was finalized, images were captured and loaded in Dvideow software (Digital for Video for Biomechanics Windows 32 bits). This program allows decentralizing the fields that compose the images of each frame of the video so that the frequency of data acquisition in this work was 50 frames per second (Barros et al., 1999; Figueroa et al., 2003).

Upon finishing the above process, the position coordinates of the markers placed over specific landmarks were determined by digitalizing each marker referenced to a three dimensional coordinate system associated to a calibration volume. The system used for calibration, was chosen according to the International Society of Biomechanics recommendations, in order to unify the kinematics data communication. Throughout a 3-D reconstruction, a three-column matrix was obtained, describing the position coordinates of the markers.

The digitalized sequence was selected from 10 step cycles of the last minute of each running speed to assure less step variability (Fisher, 2010). After establishing this sequence in one camera, we calculated the frame range to acquire the same range in all cameras. Thus to perform this, we synchronized the devices with a sound signal that was recorded in the video and read by the software. The CM coordinates were determined by 3D reconstruction analysis in Matlab 7.0^® (Mathworks, Inc.), considering the coordinates of the partial center of mass of the feet, legs, thighs, hands, forearms, arms, trunk and head. Knowing the position of the CM in each step, we proceeded to calculate the acceleration of the CM by deriving its position twice with respect to time. From the acceleration curve we determined the effective contact time for each stance phase (Cavagna, 2006). Using this time we calculate the maximum displacement (MD) of the CM from the position curve (Cavagna, 2006).

Finally, the effective vertical stiffness was determined by the ratio of the vertical acceleration peak (avmax) and MD (Brughelli and Cronin, 2008) of the CM.

Two physiological parameters were analyzed in this study (heart rate and lactate concentration). Heart rate was monitored prior to performing the experimental procedures (basal heart rate) and during both running speeds by a Nike triax c8 heart rate monitor. The lactate concentration was determined by a Roche Accutrend plus lactimeter. This device worked throughout a colorimeter method to determine the amount of blood lactate concentration. To carry out the measurement procedures we used 20 specific reagents for lactate and 20 disposable lancets (all purchased from Roche). Four lactate measurements were performed to all athletes. The first one was completed before the start up of the protocol (basal lactate concentration) and the other three were accomplished 2, 5 and 8 min after the experimental procedures were finalized.

Statistical analysis

K_vert at both speeds was plotted against athlete's time records, and lactate peak was plotted against athlete's time records.

Paired sample t-test (p < 0.01) were performed to analyze how K_vert and physiological parameters change when increasing running speed.

Pearson correlations were implemented between:

• -K_vert and physiological parameters at both speeds

• -K_vert and athlete's time records on 100 m

• -Lactate peak and athlete's time records on 100 m.

All the statistic analysis was performed in SPSS Statistics 17.0.

Results

All athletes analyzed increased their heart rate, blood lactate concentration and K_vert when enhancing running speed as established in previous investigations (Kerdok et al., 2002; Brughelli and Cronin, 2008; Fisher, 2010).

Paired sample t-tests (p < 0.01) showed significant changes in heart rate and K _vert when raising running velocity from gait transition speed to 13 km h⁻¹ (Table 1).

Table 1
Mean and standard deviation of K _vert and heart rate both running speeds p ≤ 0.01 is the significance of the change of these parameters from gate transition speed to 13 km h⁻¹.

Variable	Gait transition speed	13 km h−1	p
Kvert (s−1)	161.5 ± 22.9	194.5 ± 27.4	0.001
Heart rate	143.9 ± 11.2 bpm	177.2 ± 5.7	0.001

Also, blood lactate concentration exhibited an important peak (7.63 ± 2.41 mmol l⁻¹) 2 min after finalizing the experimental procedures which was significantly higher (p < 0.01) than the basal concentration obtained in this work (1.89 ± 0.4 mmol l⁻¹).

Pearson correlations between heart rate and K _vert for gait transition speed were higher than the ones found at 13 km h⁻¹, and lactate peak, was highly associated to K_vert values (r = 0.83) when running at 13 km h⁻¹ (Table 2).

Table 2
Results of correlations, note that the analysis are not performed for lactate peak and K _vert V1, since the samples were taken after the second race (13 km h⁻¹). The level of significance is shown between brackets.

Variable	Kvert V1	Kvert V2
Lactate peak	–	0.83 (0.000)
Heart rate	0.74 (0.001)	0.52 (0.05)

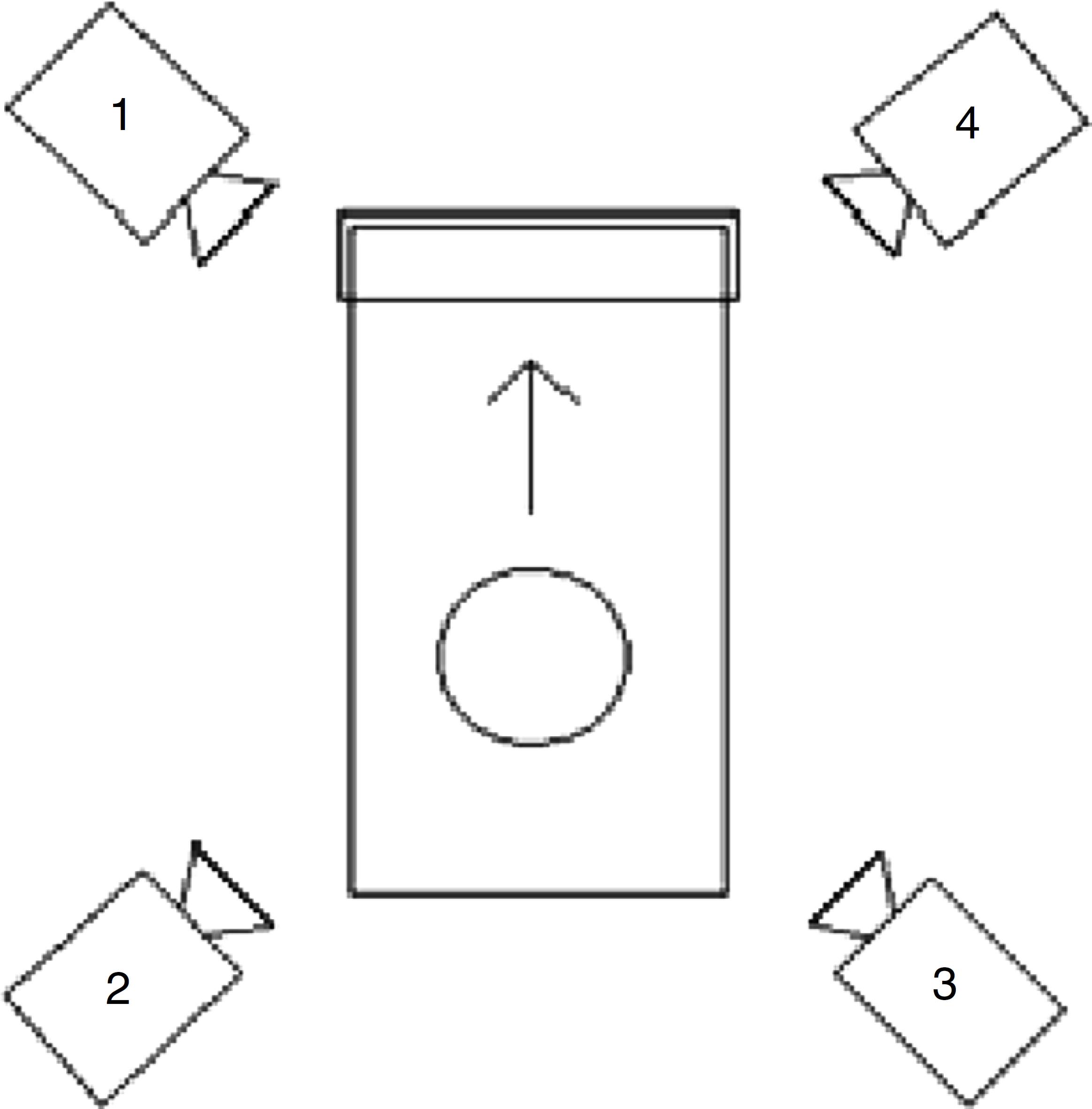
High correlations where found when plotting K _vert values measured at gate transition speed and at 13 km h⁻¹ against sprinter's time records in 100 m (r = 0.907 and r = 0.922 respectively), where the fastest sprinters (shortest time record) were the ones with the highest K_vert (Fig. 2).

Figure 2
K_vert measured at gait transition speed and at 13 km h⁻¹ vs time records in 100 m.

The same inverse relationship and similar correlation (r = 0.95) was found when plotting blood lactate peak against athlete's time records, where the fastest athletes had the highest lactate peaks (Fig. 3).

Figure 3
Lactate peak vs time records in 100 m.

Discussion

In this study, we focus on how K_vert is associated to elite athlete's performance. Therefore, to achieve this aim, we calculated K_vert and analyzed heart rate and blood lactate concentration to estimate energy consumption, considering these variables as a real feedback of physiological processes happening inside muscle tendon unit of the limbs. To estimate K_vert, we used a method based on imaging reconstruction. Although this could be considered as a limitation of the study methods since force plates are more precise, we understand it is fundamental to analyze and evaluate the study parameters at controlled speed. Thus, we considered cinemetry as the best option.

We used two different running speeds (gait transition speed and 13 km h⁻¹) to confirm that K_vert varies when increasing running velocity (Arampatzis and Metzle, 1999). We selected these running speeds since the model we are using to calculate K_vert better adjusts and is valid at low running velocities. At higher velocities, asymmetries occur in the vertical displacement of the CM during the effective ground contact phase (Cavagna et al., 1988). In this way, although we are not measuring K_vert at the usual high speed of a race, this parameter calculated at low speeds reflects the global mechanic characteristics of the athlete.

The K_vert average values found for gait transition speed (161.5 ± 22.9 s⁻²) and for 13 km h⁻¹ (194.5 ± 27.4 s⁻²), were slightly below the values usually established in previous investigations. For instance, Ferris et al. (1999) found values of 18 kN m⁻¹ (225 s⁻²) when running at 10.8 km h⁻¹ (Ferris et al., 1999); Dutto and Smith (2002) found data of 23.5 kN m⁻¹ (293 s⁻²) for a running speed of 14 km h⁻¹ (Dutto and Smith, 2002).

The difference in K_vert values found in this study from the ones reported in literature is probably associated to the method used to calculate this parameter, since in this study athletes ran on a treadmill while in most background investigations K_vert is determined by using a force platform (Brughelli and Cronin, 2008). In this way, our results included the stiffness of the treadmill (Kerdok et al., 2002) that promoted the whole body-treadmill system to become more compliant than running in a non-compliant surface. However, we found a significant increase in K_vert values (p = 0.001) when enhancing running speed which is coherent with previous studies findings (Arampatzis and Metzle, 1999; Brughelli and Cronin, 2008). The significant changes in K_vert when raising running speed have been fully explained in former studies by enhancing the force peak and decreasing the displacement of the CM during the stance phase (Brughelli and Cronin, 2008). These differences in force and displacement are determined by changes in muscular contractile capacity. This combined with metabolic changes could make the neuromuscular system regulate the muscle-tendon stiffness by increasing the level of pre-activation and thus affecting global stiffness (Fisher, 2010). It has been demonstrated that enhancing running speed, increases K_vert and as a result, a smaller amount of elastic energy is used (Brughelli and Cronin, 2008). The supporting explanation for this statement is that K_vert depends on both, the vertical acceleration and the effective deformation of the lower limb, while the elastic energy depends on the squared deformation. Therefore, the smaller effective deformation of the lower limb due to the increase on running speed becomes determinant in the use of elastic properties (Fisher, 2010). Thus, this should reflect an increase on energy consumption, as analyzed in previous studies where K_vert was assayed in different running speeds in fatigue condition (Borrani et al., 2003; Candau et al., 1998; Slawinski et al., 2008).

In this paper, we found that heart rate increases when enhancing running speed and that blood lactate concentration shows a significant peak (7.63 ± 2.41 mmol l⁻¹) compared to the basal values (1.89 ± 0.4 mmol l⁻¹), confirming that higher energy is consumed. In addition, increasing running speed implies a major effort and a greater number of muscle fibers activated, thus raising muscular activation and the force performed during the ground contact phase (Herzog, 2000). As a result, more energy (ATP) and oxygen is consumed by the muscle fibers that is supported by an intensify blood supply driven from the heart, increasing its rate and volume of ventricular ejection (Nigg et al., 2000). Pearson correlations between heart rate and K _vert for gait transition speed (r = 0.74) was higher than the one found at 13 km h⁻¹ (r = 0.52), probably because when running at a lower velocity, the main system restoring ATP is the aerobic system. On the other hand, running at a faster speed derives in a greater muscle activity implying an increase on the amount of lactate concentration. The presence of this molecule in the muscle fibers, promotes the acidification of the cells environment which speeds up oxygen release to the tissues, profiting cellular breathing (Nigg et al., 2000). We found that lactate concentration, was highly associated to K_vert values (r = 0.83) when running at 13 km h⁻¹ while heart rate correlation decreased (r = 0.52). This shows an important participation of the anaerobic system in restoring ATP.

We found that faster athletes were stiffer and also the ones that reached the highest lactate peak, thus consuming more energy. Therefore, changes in physiological variables highlight the importance of K _vert as a global parameter. Having a larger muscular volume build up by fast and explosive fibers with a larger cross section than slow fibers and a high percentage of activated fibers could determine an increase in force peak during ground contact phase leading to an increase in K _vert. This increase in muscular activation due to a larger volume will consume more energy. As a result, stiffer sprinters would consume more energy.

The findings of this study suggest that K_vert is an important determinant and a potential global parameter to evaluate sprinter's performance. Considering that it is measured when racing and simple to evaluate, this parameter has an important practical application in the coaching field. In this sense, for future studies we will focus on a longitudinal approach to analyze how different capacities such as power, explosive force and coordination can affect K_vert and athlete's performance. Up to date, there have been no studies that analyze the effects of training in other ways of estimating mechanical stiffness, such as leg stiffness, and running speed.

Conclusions

When increasing running speed, heart rate and K_vert follow the same trend of change.

At gait transition speed, K_vert is highly correlated with heart rate.

At 13 km h⁻¹ K_vert is highly correlated with lactate peak.

Our results suggest that the fastest athletes have a greater mechanical rigidity and consume more energy.

References

• Alexander R Mc N. Modelling approaches in biomechanics. Phil Trans R Soc Lond B. 2003;358:1429-35.
• Arampatzis BG, Metzle V. The effect of speed on leg stiffness and joint kinetics in human running. J Biomech. 1999;32:1349-53.
• Barros RML, Brezinkofer R, Leite NJ, Figueroa PL. Desenvolvimento e avaliação de un sistema para análise tridimensional de movimentos humanos. Rev Bras Eng Bioméd. 1999;15:234-9.
• Blickhan R. The spring-mass model for running and hopping. J Biomech. 1989;22:1217-27.
• Borrani F, Candau R, Perrey S, Millet GY, Millet GP, Rouillon JD. Does the mechanical work in running change during the VO₂ slow component?. Med Sci Sports Exerc. 2003;35:50-7.
• Brughelli M, Cronin J. Influence of running velocity on vertical, leg and joint stiffness: modeling and recommendations for future research. Sports Med. 2008;38:647-57.
• Candau R, Belli A, Millet GY, Georges D, Barbier B, Rouillon JD. Energy cost and running mechanics during a treadmill run to voluntary exhaustion in humans. Eur J Appl Physiol Occup Physiol. 1998;77:479-85.
• Cavagna GA, Franzetti P, Henglund N, Willems P. The determinants of the step frequency in running, trotting and hopping in man and other vertebrates. J Physiol. 1988;399:81-92.
• Cavagna GA. The landing-take-off asymmetry in human running. J Exp Biol. 2006;209:4051-60.
• Di Michele R, Del Curto L, Merni F. Mechanical and metabolic responses during a high-intensity circuit training workout in competitive runners. J Sports Med Phys Fitness. 2012;52:33-9.
• Dutto DJ, Smith GA. Changes in spring-mass characteristics during treadmill running to exhaustion. Med Sci Sports Exer. 2002;34:1324-31.
• Farley C, Glasheen J, Mc Mahon T. Running springs: speed and animal size. J Exp Biol. 1993;185:71-86.
• Farley CT, Gonzalez O. Leg stiffness and stride frequency in human running. J Biomech. 1996;29:181-6.
• Ferris DP, Liang K, Farley CT. Runners adjust leg stiffness for their first step on a new running surface. J Biomech. 1999;32:787-94.
• Figueroa PJ, Leite NJ, Barros RML. A flexible software for tracking of markers used in human motion analysis. Comput Methods Prog Biomed. 2003;72:155-65.
• Fisher G. Análise da Mecânica da Corrida com e sem o efeito da Fadiga [Dissertação Mestrado]. Porto Alegre: Ciências do Movimento Humano, Universidade Federal do Rio Grande do Sul,UFRGS; 2010.
• Herzog W. Cellular and molecular muscle mechanics. In: Herzog W, editor. Skeletal muscle mechanics: from mechanisms to function. New York: John Wiley & Sons, Ltd; 2000. p. 33-52.
• Kerdok AE, Biewener AA, Mc Mahon TA, Weyand PG, Herr HM. Energetics and mechanics of human running on surfaces of different stiffness. J Appl Physiol. 2002;92:469-78.
• Mcmahon TA, Valiant G, Frederick EC. Grouncho running. J Appl Physiol. 1987;62:2326-37.
• Kubo K, Ikebukuro T, Yata H, Tomita M, Okada M. Morphological and mechanicalproperties of muscle and tendon in highly trained sprinters. J Appl Biomech. 2011;27:336-44.
• Mcmahon TA, Cheng GC. The mechanics of running: how does stiffness couple with speed?. J Biomech. 1990;23:65-78.
• Morin J, Delleau G, Kyrolainen H, Jeannin T, Belli A. A simple method for measuring stiffness during running. J Appl Biomech. 2005;21:167-80.
• Morin JB, Tomazin K, Edouard P, Millet GY. Changes in running mechanics and spring-mass behavior induced by a mountain ultra-marathon race. J Biomech. 2011;44:1104-7.
• Nigg B, Mac Intosh B, Mester J. Biomechanics and biology of movement. Champaign, IL, USA: Human Kinetics; 2000.
• Saibene F, Minetti AE. Biomechanical and physiological aspects of legged locomotion in humans. Eur J Appl Physiol. 2003;88:297-316.
• Slawinski J, Heubert R, Quievre J, Billat V, Hannon C. Changes in spring-mass model parameters and energy cost during track running to exhaustion. J Strength Cond Res. 2008;22:930-6.

Publication Dates

• Publication in this collection
  Jul-Sep 2016

History

• Received
  24 July 2013
• Accepted
  12 Mar 2014