Abstracts
This paper shows the existence of a collateral equilibrium without assuming any hypotheses on the strict positivity, be they individual initial endowments, including the ex post initial endowments, or aggregated initial endowments. Because of dropping the strict positivity of social initial endowment we fail to get an equilibrium. Instead, we get a quasi-equilibrium. Then, appealing to the concept of irreducibility (introduced by McKenzie in 1959) which is adapted to the collateral model, we show that the quasi-equilibrium is indeed a legitime equilibrium.
incomplete markets; exogenous colateral; arbitrage opportunity; survival assumption
Este trabalho mostra a existência de um equilíbrio com garantias, sem assumir nenhuma hipótese sobre a positividade estrita, seja das dotações iniciais dos indivíduos (incluindo as ex-post) ou da dotação inicial agregada. Devido a esta falta de positividade estrita das dotações iniciais da sociedade, não temos um equilíbrio. Em vez disso, temos um quase-equilíbrio. Então, apelando ao conceito de irredutibilidade (introduzida por McKenzie em 1959), o qual é adaptado ao modelo com garantias, mostra-se que o quase-equilíbrio é, de fato, um equilíbrio legítimo.
mercados incompletos; colateral exógeno; oportunidade de arbitragem; hipótese de sobrevivência
Existence of collateral Equilibrium without survival assumption * Contact adress: SGAN 916 - Módulo B. ZIP Code: 70790-000 - Asa Norte - Brasília - DF. E-mail: orrillo@pos.ucb.br, jjoc@impa.br
Jaime Orrillo
Catholic University of Brasilia
Contact adress Contact adress: SGAN 916 - Módulo B. ZIP Code: 70790-000 - Asa Norte - Brasília - DF. E-mail: orrillo@pos.ucb.br, jjoc@impa.br Contact adress: SGAN 916 - Módulo B. ZIP Code: 70790-000 - Asa Norte - Brasília - DF. E-mail: orrillo@pos.ucb.br, jjoc@impa.br
ABSTRACT
This paper shows the existence of a collateral equilibrium without assuming any hypotheses on the strict positivity, be they individual initial endowments, including the ex post initial endowments, or aggregated initial endowments. Because of dropping the strict positivity of social initial endowment we fail to get an equilibrium. Instead, we get a quasi-equilibrium. Then, appealing to the concept of irreducibility (introduced by McKenzie in 1959) which is adapted to the collateral model, we show that the quasi-equilibrium is indeed a legitime equilibrium.
Keywords: incomplete markets, exogenous colateral, arbitrage opportunity, survival assumption
JEL Classification: D52
RESUMO
Este trabalho mostra a existência de um equilíbrio com garantias, sem assumir nenhuma hipótese sobre a positividade estrita, seja das dotações iniciais dos indivíduos (incluindo as ex-post) ou da dotação inicial agregada. Devido a esta falta de positividade estrita das dotações iniciais da sociedade, não temos um equilíbrio. Em vez disso, temos um quase-equilíbrio. Então, apelando ao conceito de irredutibilidade (introduzida por McKenzie em 1959), o qual é adaptado ao modelo com garantias, mostra-se que o quase-equilíbrio é, de fato, um equilíbrio legítimo.
Palavras-Chave: mercados incompletos, colateral exógeno, oportunidade de arbitragem, hipótese de sobrevivência
1 Introduction
The word "survival" implies the existence of some event that causes hurt or the loss of something that prevents some activity after the catastrophe passes (catastrophe, in this case, means the lack of future income of all the agents). The classic models of general equilibrium with uncertainty assume that agents have strictly positive initial endowments including the ex post initial endowments (or its more weaker version which declares the aggregated initial endowments to be strictly positive). Strict positivity of initial endowments of all the agents is fundamental to guarantee the existence of equilibrium. However, in the real world there is no one or nothing that guarantees agents will have some income allowing them to trade after uncertainty is solved, unless there is some mechanism which allows the transfer of positive wealth from one period to another. This mechanism could be financial markets. However, such financial institutions do not guarantee that the ex post wealth is at least non-negative, since the ex post financial income (due to asset returns) might be negative enough to create a non-positive total income. In this paper we will analyze such transfers in a GEI model by allowing agents to default on their promises. For this reason we require from borrowers to put aside collateral which will assume to be durable as in Geanakoplos and Zame (2002, 20071 1 Version more recent. ) (henceforth GZ).
Collateral, as a means to enforce promises, has been analyzed in the context of general equilibrium with incomplete markets by GZ (2002, 2007). They stress the importance of requiring collateral from borrowers each time the latter sell assets, stating that this has profound impacts on the whole economy even when there is no default).2 2 For a broad discussion on collateral, we refer to Geanakoplos (1997). In the GZ paper several examples are offered which illustrate diverse situations, from consumption distortion to the effect on the volatility of prices of both assets and commodities.
The objective of this paper is to show existence of equilibrium without assuming any assumption on the strict positivity of the initial endowments including the ex post initial endowments or aggregated initial endowments. That is, the survival assumption, which states that all individuals who have either strictly positive initial endowments or initial social endowments belong to the interior of the consumption set, is dropped. Due to this fact we do not obtain an equilibrium but rather a quasi-equilibrium.
We adapt the notion of quasi-equilibrium for a collateral economy in the same way that Gottardi and Hens (1996) do for the case of a standard incomplete market model. They proved the existence of equilibrium in a GEI model with numeraire assets while still assuming that at least one agent has strict positive initial endowments in at least one state of nature. They use the concept of irreducibility according to McKenzie (1959) to redistribute income among all the agents so that a quasi-equilibrium becomes a legitimate equilibrium. We also use this concept of irreducibility adapted to the collateral model to get our result.
However, it is useful to stress that, contrary to Gottardi and Hens (1996), we do not assume strict positivity of initial endowment of any agent. To be more precise, all agents, in this paper, are assumed to have second-period initial endowments equal to zero implying contingent income zero for all agents. Besides the fact that it is not very realistic to assume that at least one agent has positive wealth in an environment with uncertainty, it also provokes a serious technical problem in the agents' budget correspondence, namely, they fail to be lower hemi continuity. However, in the collateral model this problem disappears due to depreciation structure of goods assumed here.
The methodology used to show the existence of equilibrium is as follows: first we slightly modify the initial endowments of our original collateral economy so that in the new parameterized economy all the hypothesis imposed by GZ (2002, 2007) are satisfied. So our parameterized economy has an equilibrium. Next, by a limit process we show that the allocation of the limit economy is a quasi-equilibrium supported by a non-zero commodity-asset price system. We then use the fact that the depreciation of the first-period social endowment is strictly positive, like in GZ (2002, 2007) together with the market clear conditions to show that at least one agent has a strictly positive income. Since the agents' utility functions are strictly increasing the above agent with positive income will be maximizing his/her utility in the limit economy. Also, all the prices in the limit economy are strictly positive. Finally, to reach equilibrium in the limit economy we use the concept of irreducibility, in the context of a collateral economy, introduced by McKenzie.
The plan of the paper is as follows: in section 2 we describe the model by stating the hypotheses and defining equilibrium, quasi-equilibrium and the concept of irreducibility in our setting. In it we also establish the determinateness of individual behavior and define the arbitrage condition. Section 3 is dedicated to the proof of the existence of both quasi-equilibrium and equilibrium in the collateral economy. Section 4 offers some conclusions. We end with an appendix containing a miscellaneous of notations.
2 The Model
We shall follow, for the most part, Geanakoplos and Zame's model (see GZ, 2002) with slight differences in the notation.3
3
Actually, the notation comes from the old version of this model, namely Geanakoplos, Zame, and Dubey (1995).
To understand our notation, see the beginning of the appendix. We consider a two-period exchange economy with a finite number H of consumers and L commodities. There are S states of nature to be revealed in the second period, and in the first period there is just one state of nature (called state 0), in which H agents trade in L commodities and J assets. Default is allowed and the lenders are protected by a collateral structure which is exogenously given and backs short sales issued by the borrowers. More precisely, the collateral is modelled by a physical commodity bundle  where the j - th vector backs the sale of one unit of asset
where the j - th vector backs the sale of one unit of asset  . It is assumed that
. It is assumed that  is depreciated according to a state - contingent positive linear transformation,
is depreciated according to a state - contingent positive linear transformation,  . Let us denote by
. Let us denote by  the matrix that represents the above positive linear transformation which is
the matrix that represents the above positive linear transformation which is  column.
column.
Each asset  is characterized by its promise
is characterized by its promise  and by the collateral
and by the collateral  that backed it. Agents are characterized by their utility function
that backed it. Agents are characterized by their utility function  and their first- period initial endowments
and their first- period initial endowments  Since default is permitted, each agent has the option of delivering less than he promised. If we assume that the commodity price system is
Since default is permitted, each agent has the option of delivering less than he promised. If we assume that the commodity price system is  , the value of the promise, in each state S, is
, the value of the promise, in each state S, is  denote what agent h decides to deliver. As the only consequence of default is the seizure of the collateral, it then follows that any rational borrower will choose to deliver the minimum of the face value and the depreciated collateral value. Similarly, each lender expects to receive only the minimum between the contingent claim and the depreciated collateral value. Thus, the delivery on asset j in the second period is defined as
denote what agent h decides to deliver. As the only consequence of default is the seizure of the collateral, it then follows that any rational borrower will choose to deliver the minimum of the face value and the depreciated collateral value. Similarly, each lender expects to receive only the minimum between the contingent claim and the depreciated collateral value. Thus, the delivery on asset j in the second period is defined as
Define by  to be the matrix
to be the matrix
where the sub- matrix pY is of order s×L whose (s,l) entry is the number  In a similar way D and pYC-D are the sub-matrixes of order SxJ whose (s,j) entries are, respectively, the numbers
In a similar way D and pYC-D are the sub-matrixes of order SxJ whose (s,j) entries are, respectively, the numbers  and
and  Denote by
Denote by  the sub-space generated by the columns of the matrix R just defined.
the sub-space generated by the columns of the matrix R just defined.
We assume that
-
Each agent
 has a continuous, concave, and strictly increasing
has a continuous, concave, and strictly increasing4 4 GZ (2002) makes a weaker hypothesis. utility function
-
 and
and
To understand the meaning of the sub-index "-o", see the miscellaneous notation in the appendix.
Notice that we do not require strict positivity of the initial social endowment in contrast to GZ (2002) who do require it.
A price system is a vector  of securities, and a state-contingent consumption price vector is
of securities, and a state-contingent consumption price vector is 
Definition 1: Given a price system  a consumption-portfolio choice
a consumption-portfolio choice  is budget-feasible for agent
is budget-feasible for agent  if
if
The budget constraint (1) states that the cost of a net purchase of goods  plus the lending πθ (due to the purchase of assets) cannot exceed the borrowing πφ (due to sale of assets). The budget constraint (2) tells us that after
plus the lending πθ (due to the purchase of assets) cannot exceed the borrowing πφ (due to sale of assets). The budget constraint (2) tells us that after  occurred at date 1, the consumer must again decide on his net purchases of goods
occurred at date 1, the consumer must again decide on his net purchases of goods  , which must be financed from receipts of assets that he purchased in the first period and from net deliveries the agent makes on assets he sold.
, which must be financed from receipts of assets that he purchased in the first period and from net deliveries the agent makes on assets he sold.
Consumption-portfolio choices satisfying the budget constraint (1) and (2) define consumer h' budget set:
Definition 2: Given  , a budget-feasible choice
, a budget-feasible choice  for agent h is optimal if there is no budget-feasible choice
for agent h is optimal if there is no budget-feasible choice  for agent h such that
for agent h such that
Remark: The optimality of  for agent h can be stated in an equivalent way, as follows:
for agent h can be stated in an equivalent way, as follows:
Since the optimal is budget feasible it follows that
Therefore the previous implication becomes
We define an economy as a collection of individuals, a financial structure5 5 Consisting of promises and exogenous collateral. , and a depreciation structure. In symbols we have
It is useful to point out that agents in the economy only have initial endowments at the beginning of the economic activity.
Definition 3: (Exogenous Collateral Equilibrium)
An exogenous collateral equilibrium is a price system  , and a collection
, and a collection  of optimal choices for the respective agents. In addition, given
of optimal choices for the respective agents. In addition, given  , all markets clear:
, all markets clear:
Let
be the set of all feasible allocations. Notice that we have put short sales as part of feasible allocation since the demand for durable goods used for collateral depends on short sales.
The question is now to know whether there is a price system for which there exists an equilibrium on E. To obtain this we need to make some assumptions based on the characteristics of our economy.
What we will first demonstrate is the existence of a quasi-equilibrium for our collateral economy which is a weaker notion than that of equilibrium. Before providing assumptions for our model we are going to define what a quasi-equilibrium means in our context.
Definition 4: (Exogenous Collateral Quasi-equilibrium)
An exogenous collateral quasi-equilibrium is a price system  , and a collection
, and a collection  of budget-feasible choices for the respective agents. In addition, given
of budget-feasible choices for the respective agents. In addition, given  , all markets clear as in Definition 3 and for each agent
, all markets clear as in Definition 3 and for each agent  we have
we have
for all fixed
and
implies
The only difference between equilibrium and quasi-equilibrium is that any choice which is strictly preferred to  and budget-feasible in each state of nature of the second period must cost at least the value of the first-period initial endowment.
and budget-feasible in each state of nature of the second period must cost at least the value of the first-period initial endowment.
Under (A1) the investor's problem has a solution if, and only if, there are no arbitrage opportunities, see Orrillo (2005). That is, if and only if the following condition is satisfied:
The following characterization of NAC is given in the following lemma due to Araujo et al. (2005).
Lemma 1: There are no arbitrage opportunities if and only if  such that
such that
Notice that (3) above implies
Since utility functions are assumed to be strictly increasing by (A1), commodity prices equal to zero will be ruled out by assumption. We will make the following assumptions which will assure the existence of equilibrium without survival assumption.
Remarks:
1. As the collateral is the only method of enforcing promises (A3) is quite natural: any asset which demands no collateral requirement would deliver nothing, and therefore will have zero price in equilibrium. Assumption (A4) assures that in the second period, in any state of nature, the value of first -period initial social endowment6 6 Of course, transformed via Ys. is strictly positive for any price
Now if we want to relax (A4) to become
instead of
we would have to impose a stronger structure on
Namely,
2. Assumption (A5) assures the existence of at least one portfolio7 7 Indeed any (θ, φ) ∈ with θ ≠ 0.
which is always desirable. i.e., a portfolio yielding a non-negative, non-zero pay-off. To see this, notice that
implies that
is strictly positive and bounded away from zero. This together with (3) also implies that
. In fact:
Define the sets
These sets are all nonempty by (A3) and (A5) respectively. Since
one easily has that
Using the above fact one has that
Define αsj to be the minimum between
This parameter, αsj, is strictly positive. From the definition of
it then follows that
This implies that
for all s. This in turn implies that consumers will never be satiated in their asset demand. See assumptions A.3. in Gottardi and Hens (1996).
3. Let A be the set of all commodity - asset prices
that admit no arbitrage opportunity. That is, those which satisfy Corollary 1. Denote by N the set
If there is no confusion each time that we write
it will be understood that
will belong to N and the prices
will belong to
The prices
can be assumed to belong to
without loss of generality since the second-period budget constraint is unchangeable when
is substituted by
for all
4. It is easy to check that for any
the set N is convex.8 8 Indeed N is a cone. Thus, so is the set
To abbreviate the notation we will write  instead of
instead of 
It is convenient to decompose the individual budget set of agent h into two sets: Namely, the set
is the set of date 0 admissible trades. Note that in this set it is not assumed9 9 In contrast to Gottardi and Hens (1996) who do assume and form part of it. that the ex post income is non negative since in the collateral model the ex post financial income is always non-negative. i.e.,
In a similar way the sets of spot s admissible trades are defined to be
The next assumption requires that for all admissible10 10 Which excludes prices equal to zero since utility functions are strictly increasing by (A1). first-period commodity prices and all asset prices in the closure of N for at least one agent, the set of budget feasible asset trades has a nonempty interior.
(A6) For all  such that the interior of his/her first-period budget set
such that the interior of his/her first-period budget set  defined by
defined by
is nonempty.
Similar to Gottardi and Hens Assumption (A6) guarantees that a minimum wealth condition is always satisfied for at least one agent. For now we are not concerned with the strict positivity of the ex post financial income in a given state because this problem will be treated later in Step 2 of the demonstration of Theorem 1.
To end the description of the model we must assume that the economy is resource related. This assumption demands that any subset of individuals be endowed with resources which can be redistributed to the complementary subset of individuals so as to improve their welfare at any feasible allocation, taking into account the constraints arising from the default, collateral and market incompleteness.11 11 Incompleteness in the collateral model is defined the same way as in the standard GEI model with the only difference being that in the collateral model an asset is defined by its promise and the collateral that backs it.
Denote by
the set of all non-trivial partitions of the agents H.
Irreducibility Assumption
We are now ready to establish the notion of irreducibility in our context:
with strict inequality for some
Assumption (A7) states that at all relevant prices a minimum wealth condition holds for all agents.
3 The Existence Theorem
Now we are ready to demonstrate our main theorem. We do it in several steps:
Theorem 1: Under Assumptions A1-A7 the economy E has an exogenous collateral equilibrium.
Proof:
Step 1: Existence of quasi-equilibrium
Define, for all  the following economy sequences
the following economy sequences
where  and
and  Notice that all the assumptions listed in GZ (2002), p. 10 are satisfied. Thus from GZ (2002) it follows that each economy
Notice that all the assumptions listed in GZ (2002), p. 10 are satisfied. Thus from GZ (2002) it follows that each economy  has an equilibrium. Thus, a price system
has an equilibrium. Thus, a price system  and an allocation of consumption and investments
and an allocation of consumption and investments  exist such that
exist such that
and  maximize
maximize  subject to
subject to
It is useful to point out that in GZ (2002) the set N does not appear explicitly. The optimality condition of each consumer, in each economy  implies that the prices
implies that the prices  See Orrillo (2005).
See Orrillo (2005).
From the remark of Definition 2, the optimality of  is equivalent to the two following conditions: for all
is equivalent to the two following conditions: for all  one has
one has
Notice that under A1, Item 2 of remark12 12 Which concludes that consumers will never be satiated in their assets demand. of Assumption (A5), (4) and (5) imply the validity of
Letting13
13
Passing to a subsequence if necessary.
 from the compactness of the price domain, the non-nullity of collateral and the feasible allocations set one has
from the compactness of the price domain, the non-nullity of collateral and the feasible allocations set one has
where markets clear at the original economy E
As in Gottardi and Hens (1996), we can take limit (passing to a subsequence if necessary) when  in14
14
Notice that in (4) and (6) the continuity of agents'utility functions has been used .
(4), (5) and (6). Thus, one has that for all
in14
14
Notice that in (4) and (6) the continuity of agents'utility functions has been used .
(4), (5) and (6). Thus, one has that for all  the following is true:
the following is true:
Conditions (7) and (8) say that agents' asset holdings and consumption levels are minimizing expenditure, respectively, at date 0 and at date 1 in state  Thus we can claim that
Thus we can claim that  is a quasi-equilibrium for our exogenous collateral economy E.
is a quasi-equilibrium for our exogenous collateral economy E.
Step 2: From quasi-equilibrium to equilibrium
Assumption (A4) and market clear conditions in both asset markets and first-period commodity markets imply that there is at least one agent  for which
for which
otherwise  contradicting (A4). This implies that
contradicting (A4). This implies that  is nonempty. Thus a standard argument implies that cost minimization (9) implies utility maximization. That is, (6) holds in each state for
is nonempty. Thus a standard argument implies that cost minimization (9) implies utility maximization. That is, (6) holds in each state for  when
when  and
and  Strict monotonicity then implies that
Strict monotonicity then implies that 
In what follows we prove that (4) and (5) remain held15
15
That is,
are optimal choices for the respective agents.
at  This together with (6') will imply that the quasi-equilibrium found is an equilibrium.
This together with (6') will imply that the quasi-equilibrium found is an equilibrium.
From (A6) it follows that at prices  there is at least one agent
there is at least one agent  who can afford the portfolio
who can afford the portfolio  such that
such that  Thus the interior of
Thus the interior of  is nonempty. Cost minimization (7) then implies utility maximization (4). Strict monotonicity again then implies that
is nonempty. Cost minimization (7) then implies utility maximization (4). Strict monotonicity again then implies that  and
and 
Step 3: The non-emptiness of the interior of set  for all agents
for all agents
We will show that  the interior of
the interior of  is nonempty. This ends the proof of the main theorem. (In fact), define the following sets
is nonempty. This ends the proof of the main theorem. (In fact), define the following sets
From (A6) it follows that  is a nonempty set. Therefore,
is a nonempty set. Therefore,
Suppose that the claim is false, that is  Therefore the partition
Therefore the partition  is not trivial. Then, from (A7) we can guarantee the existence of transfers
is not trivial. Then, from (A7) we can guarantee the existence of transfers  with
with  and the existence of first-period consumption - investment
and the existence of first-period consumption - investment  such that
such that
Furthermore,
and
with strict inequality for some
We also know that  is a quasi-equilibrium . Therefore from (10) and (11) it follows that
is a quasi-equilibrium . Therefore from (10) and (11) it follows that
On the other hand, (A6) implies that  maximizes the utility of agents of
maximizes the utility of agents of  Thus,
Thus, 
and
implies
Summing among all agents of  we have
we have
The following is true
 . The last equality implied by (10) and by the fact that
. The last equality implied by (10) and by the fact that  Using these previous facts inequality (16)implies
Using these previous facts inequality (16)implies
In consequence, there exists  such that
such that
In other words
which implies that  which is a contradiction because
which is a contradiction because  This contradiction, however, is caused for having supposed
This contradiction, however, is caused for having supposed  Finally
Finally  Thus, the claim follows and the theorem as well.
Thus, the claim follows and the theorem as well.
4 Conclusions
In this paper we have demonstrated the existence of collateral equilibrium in a GEI model with default and collateral when the agents have no future income and the first-period social initial endowment is the boundary of the consumption set. Due to the fact that the first-period social initial endowment is not strictly positive, Geanakoplos and Zame's (2002) existence theorem cannot be applied.
The non satiated condition of the asset demand of consumers in this paper is implied by assumptions on collateral, assets structure and structure depreciation instead of being an hypothesis as in Gottardi and Hens (1996).
(Recebido em novembro de 2009. Aceito para publicação em setembro de 2010).
* It is useful to note that the meaning of the word "survival'' in this article is related to the positivity of consumers' initial endowments and not to their staying or expulsion from the market which depend on their beliefs, as studied by Sandroni 2000. The author acknowledges CNPq for financial support 304663/2007-7. The author is indebted to an anonymous referee for very helpful suggestions, particularly with regard to exposition of the paper.
Appendix A
A.1 Miscellaneous Notation
Let  be a vector. We write
be a vector. We write  to mean that
to mean that  and
and  The vector
The vector  is the vector x where the j- coordinate has been drooped. The same holds for bundles of vectors. If
is the vector x where the j- coordinate has been drooped. The same holds for bundles of vectors. If  then
then  is the bundle x where the k- th vector of
is the bundle x where the k- th vector of  has been drooped. By abuse of notation, we always use the same letter for both set and its cardinality. Thus, we will always write:
has been drooped. By abuse of notation, we always use the same letter for both set and its cardinality. Thus, we will always write:  . For
. For  and
and  , we set:
, we set:  . For any two vectors
. For any two vectors  is the usual scalar product. Therefore,
is the usual scalar product. Therefore, 
The set  is the non-negative simplex of
is the non-negative simplex of  and
and  is the interior of the simplex
is the interior of the simplex  . The map
. The map  is the linear projection on the i - th and j - th factors defined as
is the linear projection on the i - th and j - th factors defined as  If
If  is a matrix of order mxn and
is a matrix of order mxn and  are any two vectors, in the product
are any two vectors, in the product  , the vector
, the vector  will be a line vector and y a column vector. Finally,
will be a line vector and y a column vector. Finally,  is the vector whose coordinates are all equals 1.
is the vector whose coordinates are all equals 1.
- ARAÚJO, A.; FAJARDO, J.; PÁSCOA, M, R. Endogenous collateral. Journal of Mathematical Economics, v. 41, n. 4-5, p. 439-462, 2005.
- GEANAKOPLOS, J. Promises, promises. In: ARTHUR, W.B.; DURLAUF, S.; LANE, D. (Ed.). The economy as an evolving complex system, II Reading MA: Addison-Wesley, 1997, p. 285-320. (CFDP 1143 and CFP 1057).
- GEANAKOPLOS, J.; ZAME, W. Collateral and the enforcement of intertemporal contracts 2002. (Yale University Working Paper).
- GEANAKOPLOS, J.; ZAME, W.; DUBEY, R. Default, collateral, and derivatives. Yale University, 1995. Mimeo.
- GOTTARDI, P.; THORSTEN, H. The survival assumption and existence of competitive equilibria when asset markets are incomplete. Journal of Economic Theory, v. 71, n. 2, p. 313-323, Nov. 1996.
- HILDENBRAND, W. Core and equilibria of a large economy Princeton: Princeton University Press, 1974.
- MCKENZIE, L. W. On the existence of general equilibrium for a competetive markets. Econometrica, v. 27, p. 54-71, 1959.
- ORRILLO, J. Collateral once again. Economics Letters, v. 87, issue 1, p.27-33, April 2005.
- SANDRONI, A. Do markets favor agents able to make accurate predictions? Econometrica, v. 68, n. 6, p. 1303-1341, Nov. 2000.
- WERNER, J. Equilibrium in economics with incomplete financial markets. Journal of Economic Theory, v. 36, p. 110-119, 1985.
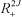 with θ ≠ 0.
with θ ≠ 0. 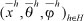 are optimal choices for the respective agents.
are optimal choices for the respective agents.Publication Dates
-
Publication in this collection
28 Apr 2011 -
Date of issue
Mar 2011
History
-
Received
Nov 2009 -
Accepted
Sept 2010


























































