Studies of electron-molecule collisions using the Schwinger variational principle with plane waves as a trial basis set

Studies of electron-molecule collisions using the Schwinger variational principle with plane waves as a trial basis set

Jorge L. S. Lino

Núcleo de Pesquisas em Matemática e

Matemática Aplicada, Universidade Braz Cubas,

Campus I, 0877-380 Mogi das Cruzes, São Paulo, Brazil

Marco A. P. Lima

Instituto de Física, Unicamp,

13083-970 Campinas, São Paulo, Brazil

Received 10 February, 2000

We report elastic differential cross sections (DCS) for the scattering of electron by H

₂

, CH

₄

, C

₂

H

₄

, SiH

₄

, and H

₂

O in the 5 to 20 eV energy range. These cross sections were obtained using the Schwinger variational principle. In our procedures the scattering wave function is expanded as a combination of plane waves. In the present implementation the exchange potential and polarization effects are not considered and all results are obtained at the static level of approximation. For all molecules, except H

₂

, our calculated DCS agree reasonably well with avaliable experimental data and with other theoretical results (obtained at the static-exchange level of approximation). Our study suggests that the Schwinger variational principle with plane wave expansion may become an efficient method for studying electron-molecule scattering.

Among the first-principle methods, the Schwinger variational principle (SVP) [1] has received special attention in the last couple of decades. The first calculations using the SVP for electron-molecule scattering were presented by McKoy and co-workers using a separable form for the Green's function [2]. To account for polarization effects and multichannel coupling (due to inelastic processes involving energetically open electronic excited states), Takatsuka and McKoy introduced modifications into the SVP and created the so called Schwinger Multichannel Method (SMC)[3]. Several applications of this method are reported in the literature [4]. Later on, studies using the SMC method with norm conserving pseudopotentials [5] were shown to be very useful for molecules containing heavy atoms [6]. In addition to applications of Schwinger Variational type of methods, several other studies using iterative procedures (ISVP) to solve the Lippmann-Schwinger equation have also been applied to electron-molecule scattering calculations [7-11]. The main limitation of the method (SVP or SMC) resides on what makes it a general method: the expansion of the scattering function is done in a L² basis (Cartesian Gaussian functions) and this is very effective only for short-range potentials. An important development of the method would be to allow inclusion of plane waves (PW) in the scattering basis and this is the motivation of the present paper. In order to do this, we have developed computer codes involving matrix elements of the type < 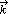_f | VG₀⁽⁺⁾V | 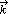_i > (second-Born type of terms) with no restrictions on molecular geometries [12, 13]. In this paper we present results for e^- - H₂, CH₄, C₂H₄, SiH₄, and H₂O scattering in the static approximation in the (5-20)-eV energy range. Although the correct treatment of exchange and of polarization effects is known to be important for low-energy scattering, we surprisingly found that the present static results are in very good agreement with experimental data for all molecules of the above list, except for H₂ at 5 and 10 eV, and for CH₄ at 5 eV. Our results are also useful to establish benchmark calculations at the static level of approximation, indispensable in the development of a more complete formalism including exchange and polarization effects. Other particular interest is to check if the SVP using plane waves is capable, for instance, of describing correctly the structures in the DCS. Here after, we will refer the SVP using plane waves as SVP-PW.

In the SVP for electron-molecule elastic scattering, the bilinear variational form of the scattering is

Here | S

_i > is the input channel state represented by the product of a plane wave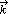 _i times |F₀ > , the initial (ground) target state. | S

_f > has analogous definition, except that the plane wave points to 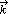_f, V is the interaction between the incident electron and the target, G₀⁽⁺⁾ is the projected Green's function, written as in the SMC method [14]:

H₀ is the Hamiltonian for the N electrons of the target plus the kinectic energy of the incident electron and E is total energy of the system (target + electron). The scattering states | Y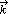_i⁽⁺⁾ > and < Y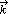_f^(-) | are products of the target wave function |F_o > and one-particle scattering wave function. The initial step in our SVP calculations is to expand the one-particle scattering wave functions as a combination of plane waves. So, in the static approximation, for elastic scattering, the expansion of the scattering wave function is done in a discrete form as

The inclusion of these definitions in Eq. (1) and the application of a stationarity condition [1, 13] with respect to the coefficients, gives the working form of the scattering amplitude:

where

We have implemented a set of computational programs to evaluate all matrix elements of Eq. (5). The Green's function given in Eq. (2) and its associated discontinuities have been examined and treated in a similar way as in the subtraction method [15, 14, 13]. Our discrete representation of the scattering wave function (given by Eqs. (3) and (4)) is made only in two dimensional space (spherical coordinates, using Gaussian quadratures for q and f and the on-shell k value for the radial coordinate). To illustrate, we present results of applications of the present method for elastic scattering of electrons by H₂, CH₄, C₂H₄, SiH₄ and H₂O, for several impact energies (from 5 to 20 eV). For all molecules we used Hartree-Fock calculations to represent the ground state of the targets with the same Cartesian Gaussian basis set expansion that have been used in previous calculations with the SMC method (Ref. [16] for H₂, Ref. [17] for CH₄, Ref. [18] for C₂H₄, Ref. [19] for SiH₄, and Ref. [20] for H₂O).

Fig. 1 shows our DCS for H₂ along with selected experimental data ([21, 22]). As noted, at 5 eV the absence of exchange and polarization contributions causes an overall underestimation of the calculated cross section. Above 10 eV, the SVP-PW generally agree well with the experimental data, except at near forward direction, where the long-range polarization potential plays a special role.

Fig. 2 shows our DCS for CH₄ with experimental data of Tanaka et al. [23]. Theoretical cross sections using static-exchange (SE) approximation with the Schwinger Multichannel Method [24] and iterative Schwinger Method [25] are also included for comparison. Again, the differences at 5 eV are expected, due to the fact that we are neglecting exchange and polarization effects. Above 5 eV, however, the comparison between our results and theoretical results [24, 25] is in general quite satisfactory.

Fig. 3 shows our DCS for C₂H₄ along with experimental data ([26]) and theoretical results obtained with the Schwinger Multichannel Method [18] and iterative Schwinger Method [27], both at the static-exchange plus polarization (SEP) level of approximation. As noted, for all energies, our DCS are reasonably close to the experimental and theoretical results.

Fig. 4 shows DCS for SiH₄. Again, for all energies, our results using the SVP-PW at the static level of approximation are very close to experimental results [29] and to theoretical results obtained at the static-exchange level of approximation with the SMC method [19].

Finally, Fig. 5 shows DCS for H₂O. Theoretical studies [30-33] are also included for comparison whenever available. As expected for H₂O, due to the permanent dipole moment, our cross sections show very strong forward-peaking. Agreement between our calculated cross sections and available experimental data is generally good. Our results also agree quite well with other theoretical studies over the angular and energy regions covered here.

In summary, although exchange potential and polarization effects are not taken into account in our calculations, our results are, in general, in good agreement with experimental and other theoretical methods for elastic electron scattering of H₂, CH₄, C₂H₄, SiH₄, and H₂O over the range of aproximately 5 to 20 eV. In the future, we plan to extend the present method to investigate the the lower-energy scattering range from 0 to 5 eV. This will be done by implementing the plane wave expansion in the SMC method, where exchange and polarization effects can be treated in an ab-initio form. The research of J.L.S.L. is supported by the Fundação de Amparo à Pesquisa do Estado de São Paulo (Fapesp) and Núcleo de Pesquisas em Matemática e Matemática Aplicada da UBC (Nupemap), Brazil. M.A.P.L acknowledge support from Brazilian agengy Conselho Nacional de Desenvolvimento Cientifico e Tecnológico (CNPq). These calculations were made at Centro Nacional de Processamento de Alto Desempenho (CENAPAD-Nordeste) and ITA-CTA. The authors also acnowledge Dr. L. M. Brescansin for insightful discussions.

References

[1] J. Schwinger, Phys. Rev. 72, 1763 (1947); B. A. Lippmann and J. Schwinger, Phys. Rev. 79, 469 (1950).

[2] T. N. Rescigno, C. W. McCurdy, and V. McKoy, Chem. Phys. Lett. 27, 401 (1974); T. N. Rescigno, C. W. McCurdy, and V. McKoy, Phys. Rev. A 10, 2240 (1974).

[3] K. Takatsuka,V. McKoy, Phys. Rev. A 24, 2473 (1981); K. Takatsuka, and V. McKoy, Phys. Rev. A 30, 1734 (1984).

[4] See, for example, C. Winstead and V.McKoy, Advances in Chemical Physics, Vol.XCVI, Edited by I. Prigogine and Stuart A. Rice, 1996 and references therein.

[5] M. H. F. Bettega, L. G. Ferreira, and M. A. P. Lima, Phys. Rev. A 47, 1111 (1993).

[6] See for example, the most recent publications using this method and references therein, A. P. P. Natalense, M. H. F. Bettega, L. G. Ferreira, and M. A. P. Lima, Phys. Rev. A 59, 879 (1999); M. T. do N. Varella, M. H. F. Bettega, A. J. R. da Silva, and M. A. P. Lima, J. Chem. Phys. 110, 2452 (1999); M. T. do N. Varella, L. G. Ferreira, and M. A. P. Lima, J. Phys. B 32, 2031 (1999).

[7] R. R. Lucchese and V. McKoy, J. Phys. B 12, L421 (1979); R. R. Lucchese, G. Raseev, and V. McKoy, Phys. Rev. A 25, 2572 (1982); R. R. Lucchese and V. McKoy, Phys. Rev. A 25, 1963 (1982).

[8] L. M. Tao, L. M. Brescansin, M. A. P. Lima, L. E. Machado, and E. P. Leal, J. Phys. B 23, 4331 (1990).

[9] S. K. Adhikari, Chem. Phys. Letters, 258, 596 (1996); S. K. Adhikari and K. L. Kowalski, Dynamical collision theory and its application (Academic Press, New York, 1991) and references therein.

[10] J. Horacek and T. Sasakawa, Phys. Rev. A 30, 2274 (1984).

[11] M.-T. Lee, I. Iga, M. M. Fujimoto, and O. Lara, J. Phys. B 28, L299 (1995).

[12] D. K. Watson and V. McKoy, Phys. Rev. A 20, 1474 (1979); A. W. Fliflet and V. McKoy, Phys. Rev. A 21, 1863 (1980).

[13] J. L. S. Lino, Ph. D. Thesis (1995), Instituto Tecnológico de Aeronáutica, Centro Técnico Aeroespacial, São José dos Campos, São Paulo, Brazil.

[14] M. A. P. Lima, L. M. Brescansin, A. J. R. Silva, C. Winstead and V. McKoy, Phys. Rev. A 41, 327 (1990).

[15] S. K. Adhikari and L. Tomio, Phys. Rev. C 37, 41 (1988).

[16] M. A. P. Lima, T. L. Gibson, V. McKoy, and W. M. Huo, Phys. Rev. A 38, 4527 (1988).

[17] C. Winstead, Q. Sun, V. McKoy, J. L. S. Lino, and M. A. P. Lima, J. Chem. Phys. 98, 2132 (1993).

[18] C. Winstead, P. G. Hipes, M. A. P. Lima, and V. McKoy, J. Chem. Phys. 94, 5455 (1991).

[19] C. Winstead and V. McKoy, Phys. Rev. A 42, 5357 (1990).

[20] L. M. Brescansin, M. A. P. Lima, L. E. Machado, L. M. Tao, Braz. J. Phys. 22, 221 (1992).

[21] S. K. Srivastava, A. Chutjian and S. Tajmar, J. Chem. Phys. 63, 2659 (1975).

[22] T. W. Shyn and W. E. Sharp, Phys. Rev. A 24, 1734 (1974).

[23] H. Tanaka, T. Okada, L. Boesten, T. Susuki, T. Yamamoto, and M. Kubo, J. Phys. B 15, 3305 (1982).

[24] M. A. P. Lima, T. L. Gibson, W. M. Huo, and V. McKoy, Phys. Rev. A 32, 2696 (1985).

[25] L. E. Machado, M. T. Lee and L. M. Brescansin, Braz. J. Phys. 28, 111 (1998).

[26] B. Mapstone and W. Newell, J. Phys. B 25, 491 (1986).

[27] L. M. Brescansin, L. E. Machado and M. T. Lee, Phys. Rev. A 57, 3504 (1998).

[28] T. N. Rescigno and B. H. Lengsfield, Z. Phys. D 24, 117 (1992).

[29] J. Perrin, J. P. M. Schmitt, G. de Rosny, B. Drevillon, J. Huc, and A. Lloret, Chem. Phys. 73, 383 (1982).

[30] L. E. Machado, L. M. Tao, L. M. Brescansin, M. A. P. Lima and V. McKoy, J. Phys. B 28, 467 (1995).

[31] Y. Okamoto, K. Onda and Y. Itikawa, J. Phys. B 26, 745 (1993).

[32] F. A. Gianturco, J. Phys. B 24, 3837 (1991).

[33] A. Jain and D. G. Thompson, J. Phys. B 16, 3077 (1987).

[34] W. M. Johstone and W. R. Newell, J. Phys. B 24, 3633 (1991).

[35] A. Danjo and H. Nishimura, J. Phys. Soc. Japan 54, 1224 (1985).

References

• [1] J. Schwinger, Phys. Rev. 72, 1763 (1947);
• B. A. Lippmann and J. Schwinger, Phys. Rev. 79, 469 (1950).
• [2] T. N. Rescigno, C. W. McCurdy, and V. McKoy, Chem. Phys. Lett. 27, 401 (1974);
• T. N. Rescigno, C. W. McCurdy, and V. McKoy, Phys. Rev. A 10, 2240 (1974).
• [3] K. Takatsuka,V. McKoy, Phys. Rev. A 24, 2473 (1981);
• K. Takatsuka, and V. McKoy, Phys. Rev. A 30, 1734 (1984).
• [4] See, for example, C. Winstead and V.McKoy, Advances in Chemical Physics, Vol.XCVI, Edited by I. Prigogine and Stuart A. Rice, 1996 and references therein.
• [5] M. H. F. Bettega, L. G. Ferreira, and M. A. P. Lima, Phys. Rev. A 47, 1111 (1993).
• [6] See for example, the most recent publications using this method and references therein, A. P. P. Natalense, M. H. F. Bettega, L. G. Ferreira, and M. A. P. Lima, Phys. Rev. A 59, 879 (1999);
• M. T. do N. Varella, M. H. F. Bettega, A. J. R. da Silva, and M. A. P. Lima, J. Chem. Phys. 110, 2452 (1999);
• M. T. do N. Varella, L. G. Ferreira, and M. A. P. Lima, J. Phys. B 32, 2031 (1999).
• [7] R. R. Lucchese and V. McKoy, J. Phys. B 12, L421 (1979);
• R. R. Lucchese, G. Raseev, and V. McKoy, Phys. Rev. A 25, 2572 (1982);
• R. R. Lucchese and V. McKoy, Phys. Rev. A 25, 1963 (1982).
• [8] L. M. Tao, L. M. Brescansin, M. A. P. Lima, L. E. Machado, and E. P. Leal, J. Phys. B 23, 4331 (1990).
• [9] S. K. Adhikari, Chem. Phys. Letters, 258, 596 (1996);
• S. K. Adhikari and K. L. Kowalski, Dynamical collision theory and its application (Academic Press, New York, 1991)
• [10] J. Horacek and T. Sasakawa, Phys. Rev. A 30, 2274 (1984).
• [11] M.-T. Lee, I. Iga, M. M. Fujimoto, and O. Lara, J. Phys. B 28, L299 (1995).
• [12] D. K. Watson and V. McKoy, Phys. Rev. A 20, 1474 (1979);
• A. W. Fliflet and V. McKoy, Phys. Rev. A 21, 1863 (1980).
• [13] J. L. S. Lino, Ph. D. Thesis (1995), Instituto Tecnológico de Aeronáutica, Centro Técnico Aeroespacial, São José dos Campos, São Paulo, Brazil.
• [14] M. A. P. Lima, L. M. Brescansin, A. J. R. Silva, C. Winstead and V. McKoy, Phys. Rev. A 41, 327 (1990).
• [15] S. K. Adhikari and L. Tomio, Phys. Rev. C 37, 41 (1988).
• [16] M. A. P. Lima, T. L. Gibson, V. McKoy, and W. M. Huo, Phys. Rev. A 38, 4527 (1988).
• [17] C. Winstead, Q. Sun, V. McKoy, J. L. S. Lino, and M. A. P. Lima, J. Chem. Phys. 98, 2132 (1993).
• [18] C. Winstead, P. G. Hipes, M. A. P. Lima, and V. McKoy, J. Chem. Phys. 94, 5455 (1991).
• [19] C. Winstead and V. McKoy, Phys. Rev. A 42, 5357 (1990).
• [20] L. M. Brescansin, M. A. P. Lima, L. E. Machado, L. M. Tao, Braz. J. Phys. 22, 221 (1992).
• [21] S. K. Srivastava, A. Chutjian and S. Tajmar, J. Chem. Phys. 63, 2659 (1975).
• [22] T. W. Shyn and W. E. Sharp, Phys. Rev. A 24, 1734 (1974).
• [23] H. Tanaka, T. Okada, L. Boesten, T. Susuki, T. Yamamoto, and M. Kubo, J. Phys. B 15, 3305 (1982).
• [24] M. A. P. Lima, T. L. Gibson, W. M. Huo, and V. McKoy, Phys. Rev. A 32, 2696 (1985).
• [25] L. E. Machado, M. T. Lee and L. M. Brescansin, Braz. J. Phys. 28, 111 (1998).
• [26] B. Mapstone and W. Newell, J. Phys. B 25, 491 (1986).
• [27] L. M. Brescansin, L. E. Machado and M. T. Lee, Phys. Rev. A 57, 3504 (1998).
• [28] T. N. Rescigno and B. H. Lengsfield, Z. Phys. D 24, 117 (1992).
• [29] J. Perrin, J. P. M. Schmitt, G. de Rosny, B. Drevillon, J. Huc, and A. Lloret, Chem. Phys. 73, 383 (1982).
• [30] L. E. Machado, L. M. Tao, L. M. Brescansin, M. A. P. Lima and V. McKoy, J. Phys. B 28, 467 (1995).
• [31] Y. Okamoto, K. Onda and Y. Itikawa, J. Phys. B 26, 745 (1993).
• [32] F. A. Gianturco, J. Phys. B 24, 3837 (1991).
• [33] A. Jain and D. G. Thompson, J. Phys. B 16, 3077 (1987).
• [34] W. M. Johstone and W. R. Newell, J. Phys. B 24, 3633 (1991).
• [35] A. Danjo and H. Nishimura, J. Phys. Soc. Japan 54, 1224 (1985).

Publication Dates

• Publication in this collection
  07 Jan 2002
• Date of issue
  June 2000

History

• Received
  10 Feb 2000