Comparison of a reduced order model for packed separation processes and a rigorous nonequilibrium stage model

COMPARISON OF A REDUCED ORDER MODEL FOR PACKED SEPARATION PROCESSES AND A RIGOROUS NONEQUILIBRIUM STAGE MODEL

L.G. Torres1^*, F.J.D. Martins¹ and I.D.L. Bogle2

¹DTQ-IT-UFRRJ, CEP 23890-000, Seropédica, Rio de Janeiro - RJ, Brazil,

E-mail: [e-mail], E-mail: [e-mail]

²Department of Chemical Engineering, UCL, Torrington Place, London, UK - WC1E 7JE

E-mail: [e-mail]

(Received: October 11, 1999 ; Accepted: May 18, 2000)

Abstract - The large dimensionality of the system of algebraic (and differential) equations of the models for packed distillation columns makes their solution difficult to be achieved. Aiming the solution of this problem, a reduced order model was developed for steady state packed separation processes. The model was developed transforming the differential equations of the rigorous model into algebraic equations through the use of the orthogonal collocation technique. The heat and mass transfer rates through the vapor-liquid interface were rigorously computed. The performance of this reduced order model was assessed comparing its results with those obtained with a rigorous rate based model. The results of the reduced order model were in good agreement with those from the rigorous model. Furthermore, the solution of the new model was the easiest to be obtained due to the robustness of the reduced order model.

Keywords: Modeling, distillation, packed columns, reduced model.

INTRODUCTION

There has been a constant growth in the usage of packed-bed separation columns in the chemical and petrochemical industries. Despite this, the modeling work done in packed columns is relatively small compared with the amount of work published on staged systems.

One of the best packed column design techniques is to solve directly the differential equations obtained with the application of the two-film model of heat and mass transfers. Steady state packed separation sections are frequently modeled by a system of ordinary differential equations coupled with algebraic equations and the level of complexity makes the solution hard to achieve. There have been some attempts to tackle the problem using different techniques for the numerical solution of the differential equations, namely: orthogonal collocation on finite elements, finite differences, orthogonal collocation, etc., leading to different sets of "reduced order models".

Srivastava and Joseph (1984) employed the orthogonal collocation procedure to transform the partial differential equations of the dynamic model into ordinary differential equations. Wang and Cameron (1992) extended the approach presented by Srivastava and Joseph to allow the simulation of a complete column and introduced a more rigorous procedure for the evaluation of the mass and heat transfer coefficients.

Huss and Westerberg (1996a, b) presented a major breakthrough on the development of reduced order models for plate distillation columns. The key point in the development of their model is the introduction of two variable transformations. An exponential transformation of the tray number allows one to deal with a column with a very large number of trays. On the other hand, with a hyperbolic tangent transformation of the mole fraction, the model can simulate columns which reach high purities. Some of these concepts are worth to be tested for packed columns.

The community that was normally dealing with the simulation of distillation columns was shaken with the development of the so called ‘nonequilibrium stage model’ as presented by Taylor and coworkers [Krishnamurthy and Taylor, 1985a, b, and c, Powers et al., 1988]. A very good review on this model can be found in the book of Taylor and Krishna (1993). As appropriately pointed out by Seader [Seader, 1989], practical application of the results of simulations using a equilibrium stage model by means of stage efficiency have always been suspect, mainly for multicomponent systems. The incorporation of recent developments in multicomponent mass transfer in this nonequilibrium stage models, allow us to develop a completely rate-based approach to the calculations of separation processes.

Some interesting results have been reported concerning the use of these reduced order models, but the interfacial mass transfer rates have always been computed using simplified procedures that could lead to wrong predictions. In this work, attention is focused on the development of a strategy based on a nonequilibrium stage model. The interface mass transfer rates have been computed using the linearized theory of Toor-Stewart-Prober (Stewart and Prober, 1964 and Toor, 1964a, b). The system of algebraic-differential equations produced will initially be converted to a system of algebraic equations by means of the application of the orthogonal collocation technique.

DEVELOPMENT OF THE MODEL

The reduced order model presented in this work is, to some extent, a combination of the ideas of Krishnamurthy and Taylor (1985a, b, c) and their nonequilibrium stage model with the order reduction concepts applied by Srivastava and Joseph (1984).

For the development of the model, a negligible pressure drop through the packed bed was assumed and the vapor-liquid interface was represented as a surface where there is no resistance to transfer and where equilibrium prevails. Considering the notation for the differential volume element presented in Figure 1, the following equations can be written:

a) The vapor phase and the liquid phase mass balances and the component mass balances, where V and L are the molar vapor and liquid flowrates, z_R is the spatial variable, y_i and x_i are the vapor phase and the liquid phase mole fractions, nc is the number of components, and N_i is the total interface mass transfer rate of component i.

(2)

(3)

(4)

b) The energy balances for the vapor phase, interface, and liquid phase

(5)

(6)

(7)

where H is the enthalpy, 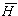is the partial molar enthalpy and q is the conductive heat transfer rate.

c) The interface relationships

(8)

(9)

where K_i is the equilibrium ratio for component i and x^I and y^I are the molar fractions at the interface.

In order to complete the model, it is necessary to state how the mass and heat transfer rates will be computed. The diffusion fluxes in the vapor and liquid phases are computed using the linearized theory of Toor-Stewart-Prober as presented by Taylor and Krishna (1993), leading to the following rate equations:

(10)

(11)

(12)

(13)

where a_e is the effective interfacial area, S is the cross sectional area of the column, c_t is the mixture molar density, [X₀] is the matrix of high flux correction factors, [G] is the matrix of thermodynamic factors, h is the heat transfer coefficient, X_H is the high flux correction on the heat transfer coefficient, and [R], the matrix function of inverted binary mass transfer coefficients, are computed using

(14)

(15)

for the vapor phase (and similarly for the liquid phase) where k_i,j is the Maxwell-Stefan mass transfer coefficient for the binary pair i-j.

Equations (1)-(13) are written for every section of the distillation column and must be solved subject to the boundary conditions of the particular section. The reduction of the order of the model is achieved applying the orthogonal collocation procedure (Finlayson, 1980) on the spatial variable. This will lead to 5nc + 5 unknown variables and equations at every collocation point. The variables are ordered in the vector (x_j) and the functions in the vector (f_j) as follows:

(16)

(17)

The system of algebraic equations of the model was solved using the subroutine C05NDF from the NAG FORTRAN Workstation Library, produced by The Numerical Algorithm Group Ltd.. Subroutine C05NDF is a comprehensive routine to find the solution of a system of nonlinear equations by a modification of the Powell hybrid method (Powell, 1970).

A thorough description of this reduced order model, alongside different ones, can be found in the work of Torres (1995).

The results obtained with this reduced order model were compared with those found using a rigorous nonequilibrium stage model as described by Krishnamurthy and Taylor (1985a, b, c). The diffusion fluxes in the vapor and liquid phases as well as all the relevant properties were computed using the same subroutines employed by the reduced order model in order to allow a proper comparison of the results.

SIMULATION EXAMPLES

For the comparison of the results obtained using the models presented in this work two selected examples were explored. In both examples, a simple packed distillation column, equipped with a total condenser and a partial reboiler, was simulated.

A key step for the simulations is the initialization of the variables. A bad initial set of variables will prevent the convergence to be reached. We made some modifications to the initialization procedure presented by Krishnamurthy and Taylor (1985c), leading to:

a) based on the guessed product compositions, the temperatures at the top and at the bottom of the column are calculated using a bubble point procedure;

b) the temperatures at any other point in the column are obtained by linear interpolation of the end values. The temperatures of the liquid phase, vapor phase, and interface will be considered the same;

c) the liquid mole fractions are also estimated by linear interpolation of the terminal values. Whenever needed, the vapor mole fractions, and the interface mole fractions are initialized with the same values for the liquid phase mole fractions;

d) the total flowrates are estimated by assuming constant molar overflow in the various sections of the column;

e) the mass transfer rates are initialized as being equal to one percent of the component flowrate at any specific location in the column. The fluxes’ signs are assigned according the components’ K-value. For K-values greater than one, fluxes are considered as negatives and positives otherwise.

Example 1

This example have been used by some researchers for testing their models (e.g. Srivastava and Joseph, 1984 and Wardle and Hapoglu, 1992). The packed column is distilling an equimolar mixture of methyl cyclohexane (MCH), toluene (Tol), meta-xylene (m-Xyl), and para-xylene (p-Xyl). The feed, a saturated liquid at the column conditions (P = 1.013 × 10⁵ N/m²), is introduced at a rate of 0.2483 moles/s. The column cross sectional area is 0.1 m² and the height of packing in both sections is 1.98 m. The column is packed with ½" ceramic Raschig rings (surface area of 368 m²/m³ and a nominal diameter of 12.7 mm). And is operated with a reflux ratio equal to 5.0, producing a bottoms flowrate of 0.1216 moles/s.

One can clearly observe in Figures 2 and 3 how well the reduced order model predicted the product compositions comparing them with those calculated by the rigorous model. As it was already expected, an increase on the number of internal collocation points employed for the approximation causes an improvement in the predictions for the internal compositions.

It is important to stress the difference in how the models deal with the feed region. In the rigorous model the feed is naturally incorporated into one of the nonequilibrium stages. On the other hand, the reduced order model deals separately with the stripping and rectification sections of the column that are linked by a mass balance working as boundary conditions. This certainly will lead to differences in the predictions for the region close to the feed.

The composition profiles employed on the initialization step can be seen in Figure 4. Each pair of curves indicates the initial profile assumed and the profile computed using the reduced order model. For every component in each section the assumed profile is linear.

It must be emphasized that the initialization procedure described before did not work for the rigorous model. In order to obtain the results using the rigorous nonequilibrium model, it was initialized with the results found using the reduced order model. It is important to highlight that, in this example, the reduced order model was capable of reaching the solution starting from a point where the whole column had the same composition as the feed stream.

The effect of the number of equations employed in the model (order of the approximation) on the relative error of the calculated product compositions can be checked analyzing the data in Figure 5. The solution obtained with a ‘high order’ model was considered as the reference for the computation of the errors. The high relative errors observed in this figure are associated to those components that are present in very small amount in that particular product. The reduced order model converges to the solution with a convergence rate higher than that observed for the rigorous model. The rigorous model approaches the solution following an asymptotic trajectory while the reduced order model follows a sinusoidal trajectory with decreasing amplitude.

Example 2

The second example deals with an industrial depropanizer which uses structured packing and was originally presented by Wang and Cameron (1991). The column is distilling a mixture of ethane (C2), propane (C3), propylene (C3=), and isobutane (i-C4). The feed is partially vaporized (97% vapor) at the column conditions (P = 1.65 × 10⁶ N/m²), is introduced at a rate of 71.94 moles/s. The mole fractions of the feed are: 0.025 (C2), 0.118 (C3), 0.349 (C3=), and 0.509 (i-C4). The column cross sectional area is 0.65 m² and the height of packing in both sections is 4.08 m. The column is packed with Mellapak 250Y (surface area equal to 250 m²/m³). And is operated with a reflux ratio equal to 3.75, producing a bottoms flowrate of 41.68 moles/s.

As one can observe in Figures 6 and 7, the reduced order model was capable of predicting, with reasonable precision, the composition of the products. However, the need for a higher order approximation, to properly calculate these compositions, is clear.

The loss of quality on the predictions of the internal compositions is also noticeable. It is our belief that this difficulty is partially due to the presence of ethane in the system. This component has in this distillation column a composition profile of the class frequently referred as "steep and flat". It is hard to fit a "steep and flat" composition profile using a polynomial approximation technique like the orthogonal collocation. We have been trying to minimize this problem following some ideas presented by Huss and Westerberg (1996a, b).

They were able to simulate plate distillation columns with "steep and flat" composition profiles using reduced order models based on collocation methods. The key point in their development is the introduction of some variable transformations aiming the elimination of the "bounce from the boundary" effect normally presented by the composition profiles obtained by polynomial approximation.

The composition profiles employed in the initialization step are presented on Figure 8 together with the solution found with the reduced order model. The initial composition profiles assumed were linear.

The convergence characteristics of the models towards the solution, observed in example 1, are present again. The initialization procedure did work very well for the reduced order model but, again, the rigorous nonequilibrium model was not able to find the solution with this starting scheme.

CONCLUSIONS

In this paper, a reduced order nonequilibrium model for packed distillation columns was described and its performance was assessed comparing its predictions with those obtained using a rigorous nonequilibrium stage model. The comparison of the results from both models indicated a very good agreement for the composition of top and bottom products. The composition profiles for the whole column are reasonably predicted by the reduced order model, except for situations where there is a component with a "steep and flat" composition profile. The convergence characteristics of the reduced order model have to be emphasized. The convergence rate of the reduced order model towards the solution increases with the number of equations of the model much faster than the rigorous model. Even more important is the fact that the initialization procedure described here worked very well for the reduced order model. The same can not be said for the rigorous model, even for the simplest example. Therefore, the reduced order nonequilibrium model presented here is very robust and, at this stage of development, its usage would be indicated when one is looking for good estimates for the compositions of the products or on the generation of starting values to initialize a rigorous nonequilibrium stage model.

ACKNOWLEDGEMENTS

This investigation was financially supported by FAPERJ (Research Foundation of Rio de Janeiro State, Brazil). F.J.D. Martins gratefully acknowledges the scholarship received from CNPq (Brazilian Council of Research and Technology).

NOMENCLATURE

English Letters

a_e effective interfacial area for mass transfer, m²/m³ c_t mixture molar density, mol/m³ f vector of functions H enthalpy, J/mol partial molar enthalpy, J/mol h heat transfer coefficient, J/(m².s.K) K equilibrium ratio (K-value) L total liquid flow, mol/s N total interphase mass transfer rate, mol/(m.s) nc number of components P pressure, N/m² q conductive heat transfer rate, J/(m.s) [R] matrix function of inverted binary mass transfer coefficients, s/m S cross sectional area of the column, m² V total vapor flow, mol/s x liquid phase mole fraction x vector of variables y liquid phase mole fraction z_R spatial variable, m

Greek letters

[G ] matrix of thermodynamic factors k Maxwell-Stefan mass transfer coefficient, m/s [X₀] matrix of high flux correction factors X_H high flux correction factor on the heat transfer coefficient

Subscripts and Superscripts

av indicates that averaged properties are employed in the evaluation of the indicated parameter I referring to the interface i referring to component i j referring to component j, referring to collocation point j k referring to component k L referring to the liquid phase V referring to the vapor phase

• Finlayson, B.A., Nonlinear Analysis in Chemical Engineering, McGraw-Hill, Inc., New York, (1980).
• Huss, R.S. and Westerberg, A.W., Collocation Methods for Distillation Design. 1. Model Description and Testing, Ind. Eng. Chem. Res., 35(5), 1603 (1996a).
• Huss, R.S. and Westerberg, A.W., Collocation Methods for Distillation Design. 2. Applications for Distillation, Ind. Eng. Chem. Res., 35(5), 1611 (1996b).
• Krishnamurthy, R and Taylor, R., A Nonequilibrium Stage Model of Multicomponent Separation Processes. Part I: Model Description and Method of Solution, AIChE J., 31(3), 449 (1985a).
• Krishnamurthy, R and Taylor, R., A Nonequilibrium Stage Model of Multicomponent Separation Processes. Part II: Comparison with Experiment, AIChE J., 31(3), 456 (1985b).
• Krishnamurthy, R and Taylor, R., Simulation of Packed Distillation and Absorption Columns, Ind. Eng. Chem. Process Des. Dev., 24(3), 513 (1985c).
• Powell, M.J.D., A Hybrid Method for Nonlinear Algebraic Equations, in Rabinowitz, P. (Editor), Numerical Methods for Nonlinear Algebraic Equations, Gordon and Breach, London, (1970).
• Powers, M.F.; Vickery, D.J.; Arehole, A.; Taylor, R., A Nonequilibrium Stage Model of Multicomponent Separation Processes V. Computational Methods for Solving the Model Equations, Comp. Chem. Eng., 12(12), 1229 (1988).
• Seader, J.D., The Rate-Based Approach for Modeling Staged Separations, Chem. Eng. Prog., 85(10), 41 (1989).
• Srivastava, R.K. and Joseph, B., Simulation of Packed-Bed Separation Processes using Orthogonal Collocation, Comp. Chem. Eng., 8(1), 43 (1984).
• Stewart, W.E. and Prober, R., Matrix Calculations of Multicomponent Mass Transfer in Isothermal Systems, Ind. Eng. Chem. Fundam., 3(3), 224 (1964).
• Taylor, R and Krishna, R., Multicomponent Mass Transfer, John Wiley & Sons, Inc., New York, (1993).
• Toor, H.L., Solution of the Linearized Equations of Multicomponent Mass Transfer: I, AIChE J., 10(4), 448 (1964a).
• Toor, H.L., Solution of the Linearized Equations of Multicomponent Mass Transfer: II. Matrix Methods, AIChE J., 10(4), 460 (1964b).
• Torres, L.G., On Some Reduced Order Models for Packed Separation Processes, Ph.D. Thesis, University of London (University College) (1995).
• Wang, F.Y. and Cameron, I.T., Modeling and Dynamics of a Distributed Fractionation Process in Petroleum Refining, Proceedings of International Confe. and Exhib. on Petro. Refin. & Petrochem. Proc., Beijing, China (1991).
• Wang, F.Y. and Cameron, I.T., Dynamics and Optimal Control of Distributed Staged Fractionators, Ichem^E Symposium Series, 128, A17 (1992).
• Wardle, A.P. and Hapoglu, H., The Use of Finite Elements in the Simulation of Packed Distillation Columns, Proceedings of the 1992 IChem^E Research Event, Manchester, England, 576 (1992).

*

To whom correspondence should be addressed

Publication Dates

• Publication in this collection
  16 Mar 2001
• Date of issue
  Dec 2000

History

• Accepted
  18 May 2000
• Received
  11 Oct 1999