A rough terrain traction control technique for all-wheel-drive mobile robots

TECHNICAL PAPERS

A rough terrain traction control technique for all-wheel-drive mobile robots

Alexandre F. Barral Silva^I; Auderi Vicente Santos^II; Marco Antonio Meggiolaro^III; Mauro Speranza Neto^IV

^IFaculdade Área 1, 41720-200 Salvador, Bahia, Brazil. [e-mail]

^IIPontifical Catholic University of Rio de Janeiro, 22451-900 Rio de Janeiro, RJ, Brazil. [e-mail]

^IIIPontifical Catholic University of Rio de Janeiro, Department of Mechanical Engineering, 22451-900 Rio de Janeiro, RJ, Brazil. [e-mail]

^IVPontifical Catholic University of Rio de Janeiro, Department of Mechanical Engineering, 22451-900 Rio de Janeiro, RJ, Brazil. [e-mail]

ABSTRACT

Traction control is a critical aspect of mobile robots that need to traverse rough terrain, avoiding excessive slip - which may cause the terrain to collapse locally and trap the robot wheels - and guaranteeing an adequate trajectory and speed control while reducing the power requirements. Traction control of all-wheel-drive robots in rough terrain was originally motivated by space exploration, such as in the case of the Mars Exploration Rovers. However, such technology is also needed in our planet, in particular in the Amazon region. This is the case of the Hybrid Environmental Robot (HER), a 4-wheel-drive mobile robot with independent suspensions, under development at CENPES/PETROBRAS. This robot is susceptible to changing terrain conditions, facing slippery soil and steep slopes. In this work, a new traction control scheme is proposed to allow HER to maintain a desired velocity while minimizing power requirements and slippage, considering motor saturation and avoiding flip-over dynamic instability. The proposed technique is based on a redundant computed torque control scheme, analytically optimized to minimize power requirements. Simulations are performed for rough terrain conditions with 2D-profile, considering the general case of different tire-terrain contact angles at each wheel. It is found that the control scheme is able to analytically predict in real time the ideal torques required by each independent wheel to maintain the desired speed, even on very rough terrain, minimizing when possible the power consumption. The method is applicable to the 3D case as long as the roll angle of the robot chassis does not vary too much compared to the robot pitch angle.

Keywords: traction control, mobile robot, rough terrain, all-wheel drive

Introduction

Since 1988 PETROBRAS explores petroleum in Urucu (AM), in the middle of the Amazonian forest. The Urucu plant is the largest Natural Gas Unit in Brazil (UPGN3), with a production of more than six million cubic meters of natural gas per day (Santos, 2007). To safely distribute this production, PETROBRAS is building two gas pipelines, Coari-Manaus (420 km long) and Urucu-Porto Velho (550 km long). In addition, PETROBRAS is developing a series of robots in the Robotics Laboratory at CENPES to monitor these almost 1000 km of pipelines.

Among the robots under development, there is the Hybrid Environmental Robot (HER, see Fig. 1), which will be used in the monitoring and data collection of the environment nearby the pipelines. Due to the several types of soils, obstacles and rough terrain that HER may face in its missions, it is indispensable to have an appropriate traction control that makes it possible to safely traverse obstacles, avoiding wheel slippage and minimizing power consumption.

The development of traction control for mobile robots has been motivated in the last years for use in several applications such as in planetary exploration (Balaram, 2000; Tarokh et al., 1999), hazardous areas with volcanic activity (Caltabiano and Muscato, 2002), materials handling (Simeón and Dacre-Wright, 1993), and even for household chores (Albagul and Wahyudi, 2004). The drive system of most mobile robots is based on wheels, due to their low power consumption, high speeds, and high load capacity (Grand et al., 2004).

Optimization of a rover chassis design to improve wheel traction has been addressed in (Thueer et al., 2007). Traction control presents a great number of research works applied to passenger vehicles moving in planar roads (Anwar, 2003).

A technique very used by the automotive industry is ABS (Anti-lock Braking System), which consists in using the information of the sliding of each wheel to correct its speed, minimizing skidding (Sakai et al., 1999). Methods based on the ABS system can be derived to be used in the control of mobile robots used in space applications (rovers) in rough terrain. However, such methods don't take into account the kinematics and the physical model of the robot, being in this way limited to benign terrain, resulting in low performance on very rough terrain. In addition, the wheel speeds are only altered when the sliding has already happened. Therefore, the system reacts with a certain delay, generating errors in the robot's location, in special if dead reckoning is used.

In Lamon and Siegwart (2005), a method is presented which proposes the minimization of the ratio between the traction and normal forces at each wheel, measured with sensors installed at the wheel, to prevent sliding. This method has the advantage of not requiring the knowledge of the soil characteristics nor of the robot's speed. Good results were obtained in simulations, although only limited experiments were performed to validate the proposed approach in real situations (Krebs et al., 2008). In addition, this approach has the inconvenience of the high cost and complexity of the required wheels.

There are also models that are based on obtaining a certain value of optimal sliding (S_cr) between the wheels and the soil in order to maximize traction force. The value of S_cr depends on the combination of tire/soil, varying considerably for different combinations (Caltabiano et al., 2004; Sarkar and Yun, 1998). Among the inconveniences of this approach are: the hypothesis of the wheel being flexible and the soil rigid, the need for the knowledge of S_cr for each combination of tire/soil, and the need to know the speed of the vehicle and the normal forces acting at each wheel. Burg and Blazevic (1997) presented an approach based on an estimate of S_cr that doesn't use the knowledge of the soil characteristics. However, it is only valid for flat terrain, being very susceptible to errors due to variations in the terrain or due to robot vibrations. Chatila et al. (1999) performed traction control based on the comparison among the wheel speeds; however, it would have a high computational cost to be applied to rough terrain.

Iagnemma and Dubowsky (2004) presented a traction control method for rough terrain that is not based on torque distribution systems nor on measures of sliding of the wheels. It just uses the properties of the soil and of its geometry to obtain the contact angle between the wheels and the ground. Using this information, the method optimizes the torque at each wheel with the intention of obtaining maximum traction or minimum power consumption, depending on the local level of difficulty/traversability of the terrain. The method presented good results in simulations and in experiments.

The present work presents a traction control scheme for mobile robots in rough terrain that also depends on the contact angles between the wheels and the ground. The proposed method is an improvement from a previous work from the authors Silva et al. (2008) dealing with tire/soil contact loss. Differently from Iagnemma's approach, it explicitly considers the robot's dynamic model, including flexible suspensions. It is able to control a desired speed V_d along the longitudinal axis of the robot's chassis (measured in the global frame), considering motor saturation and trying to avoid wheel slip and flip-over dynamic instability. In some cases, when multiple solutions for the actuation torques exist, the control can also minimize the mechanical power required by the robotic system. This minimization is automatically performed by the proposed algorithm, without the need for heuristically classifying terrains into "easy" or "difficult" as needed in Iagnemma and Dubowsky (2004).

The control method is developed and simulated for the two-dimensional (2D) case considering a generic rough terrain. The method can also be applied to a general 3D case, though it would not provide a closed form solution. It is shown that the 2D version has an explicit solution for the actuation torques. This 2D formulation can be applied to 3D robots in trajectories where the chassis roll angle is nearly constant. In the next section, the dynamic model of a 2D mobile robot is presented, considering flexible independent suspensions.

Nomenclature

a = acceleration of the vehicle center of mass, m/s² c = suspension damping constant, N.s/m CM = center of mass F = force, N g = acceleration of gravity, m/s² g(x_cc) = centers curve h = distance between wheel center and robot center of mass normal to the chassis bottom, m I = robot moment of inertia in the z direction, kg.m² K = suspension stiffness constant, N/m K_p = proportional gain L = longitudinal distance between wheel center and robot center of mass, m m = robot mass, kg M = inertia matrix of the robot N = normal force acting at each wheel, N P = robot weight, N PT = total power required by the robot, W r = wheel radius, m t = time, s T = motor torque, N.m V = velocity, m/s x = horizontal coordinate, m x_i = horizontal coordinate of wheel-terrain contact point, m y = vertical coordinate, m y_i = vertical coordinate of wheel-terrain contact point, m Greek Symbols α = slope of the robot chassis, rad = angular velocity of the robot chassis, rad/s = angular acceleration of the robot chassis, rad/s² γ = tire-terrain contact angle, rad µ = tire-terrain static coefficient of friction ξ = displacement of each suspension, m = rate of the displacement of each suspension in the direction perpendicular to the robot chassis bottom, m/s ω = angular velocity of each wheel, rad/s Subscripts cc relative to the centers curve c relative to the robot center of mass ci relative to the center of wheel i d desired value f final value i relative to wheel number i L relative to the longitudinal direction r relative to the suspension reaction sat saturation value

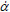
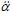
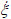
Terrain Model and Wheel Contact Angles

To generate a control law and simulate the mobile robot behavior on rough terrain, it is necessary to develop analytical models. The system model presented next assumes the hypotheses: rigid wheels and soil, inertia of the vehicle concentrated in its center of mass, negligible inertia of the suspension-wheel system compared to the robot chassis', and flexible independent suspensions, modeled as spring-damper systems.

The control method requires the knowledge of the wheel-terrain contact angles. This can be accomplished in three ways: (i) the robot can have special pressure sensors installed at the wheel rim or force sensors on the shaft, an expensive but straightforward approach; (ii) the robot can estimate these angles from the knowledge of the robot kinematics and measurements from the wheel encoders and from an inertial navigation system, merged using an Extended Kalman Filter (Iagnemma and Dubowsky, 2004); or (iii) the robot may use a map of the terrain profile, which will be assumed in this work, even though the other two methods could also be used with the proposed method.

In the third case, the terrain profile must be provided to the robot, which can be accomplished, e.g., from previously stored terrain maps, or from vision systems with the aid of laser (structured lighting) or stereo cameras. The terrain profile curve is modeled as a function f(x) formed by the union of discrete (x_i, y_i) points, see Fig. 2. Here, it is assumed that the terrain shape is continuous and that there is a unique value of y_i for every x_i. The spacing of these points along the x (horizontal) axis is constant and equal to dx. The coordinate y will be a function of x, in other words, y_i = f(x_i).

To help in the calculation of the wheel contact point with the terrain at each state of the robotic vehicle, a new curve is generated, denominated centers curve, g(x_cc). This curve is the geometric locus of the center of a rigid wheel with a known radius r, when it is rolled along keeping contact with the terrain. The points (x_cc, y_cc) of the centers curve, shown in Fig. 2, are generated from the terrain profile points. For each point (x_i, y_i) of the terrain, the point (x_cc, y_cc) is calculated such that it belongs to the line perpendicular to the tangent to the terrain profile, above the terrain, at a distance r from the contact point, see Fig. 2. The union of all calculated (x_cc, y_cc) generates the centers curve g(x_cc).

There are a few special cases where an appropriate mathematical handling must be performed to obtain the centers curve (Silva, 2007). One of these cases is when a wheel can get in contact with multiple points on the terrain, which happens when the terrain curvature radius is smaller than the wheel radius. In this situation, the contact point may abruptly change. The proposed method is robust to this change, because even though the derivative of the centers curve at such points may be discontinuous, the curve itself is still continuous.

In general, the centers curve for the terrain profile can be expressed as the union of (x_cc, g(x_cc)) points. In other words, the centers curve is a function, and each of its points can be associated to a point (x_i, y_i) of the terrain profile. Thus, to calculate the contact point between a wheel and the terrain, it will be enough to know the coordinates of the center of this wheel, find the closest match in the discretized centers curve, and then correlate it to the terrain profile points, which will be the wheel-terrain contact point. The contact angle γ_i, defined as the angle between the tangent to the terrain profile and the horizontal at the contact point of wheel i (i = 1 for the rear wheel and i = 2 for the front one) is then obtained from the discrete derivative of (x_i, y_i), see Fig. 2.

Dynamic Equations of Movement

Figure 3 shows a schematic representation of the robot to be analyzed.

From the free body diagram of the robot chassis, and applying Newton-Euler's equations, then

Neglecting the wheel inertia, Newton-Euler's equations applied to the free body diagram of each wheel i (i = 1, 2) result in:

From Eqs. (4) and (5), the values of N_i and F_ri can be obtained, resulting in

Substituting the above equations into Eqs. (1)-(3), then

The values of ξ_i and 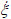_i are calculated from the current system state (x_c, y_c, α, _c, _c, 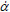) and from the coordinates of the center of wheel i, (x_ci, y_ci), which are known from the terrain profile, resulting in

Since the inertia of the wheels and suspensions is neglected, the suspension can never suffer elongation. Thus, Eqs. (12)-(13) are only valid if ξ_i < 0, with the suspension i under compression; otherwise ξ_i = 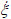_i = 0. Thus, whenever Eq. (13) is valid, the velocity components of the center of wheel i will be related by

The speed of the center of wheel i in the longitudinal direction to the chassis is

where

Substituting Eqs. (16)-(17) into Eq. (15) and using Eq. (14):

Substituting Eqs. (18)-(19) into Eq. (11) it is possible to obtain

_i as a function of the current system state and the coordinates of the center of wheel i,

The deformations and rates of deformation of the suspensions of both wheels can be then obtained from Eqs. (12) and (20). Substituting these values into Eqs. (9)-(11) above, it can be seen that the system accelerations will be a function of only the traction forces acting between the wheels and the terrain (F₁ and F₂, which are controllable from the motor torques) and of other known variables. These forces can be chosen at each time step to optimize a given system characteristics, which will be addressed next.

The Proposed Traction Control

The proposed traction control scheme, denominated here Dynamic Rough Terrain Control (DRTC), has the objective to provide wheel torques that will let the robot surpass obstacles in rough terrain while keeping a constant desired speed V_d of its center of mass in the longitudinal direction to the chassis (measured in the global coordinate frame). The control must also guarantee dynamic stability and avoid slippage, taking motor saturation into account. If more than one combination of motor torques is able to accomplish the above requirements, then the proposed control will also find the solution that minimizes the system power consumption. The control technique is described next.

Calculation of the Acceptable Wheel Traction Forces

The control method first searches for motor torques that can generate appropriate traction forces F₁ and F₂, at the same time considering motor saturation and avoiding slippage and loss of wheel contact. These conditions can be written through the following inequalities:

a) |F₁| < F_sat1, to consider saturation of the motor of wheel 1, where F_sat1 is the motor saturation torque divided by r; if motor saturation is undesirable, then F_sat1 can be chosen slightly smaller than the saturation value;

b) |F₂| < F_sat2, to consider saturation of the motor of wheel 2; once again, if motor saturation is undesirable, then F_sat2 can be chosen slightly smaller than the saturation value;

c) N₁> 0, condition for wheel 1 not to lose ground contact;

d) N₂> 0, condition for wheel 2 not to lose ground contact;

e) |F₁| < µ · N₁, to avoid wheel 1 slippage, where µ is the equivalent wheel-terrain static friction coefficient; and

f) |F₂| < µ · N₂, to avoid wheel 2 slippage.

Substituting i = 1, 2 into Eq. (7), then conditions c) and d) result in:

It can be seen that, for a given system state, all conditions above are bounded by vertical or horizontal lines in the F₁ × F₂ plane. Therefore, the intersection of all regions above can only result in either a rectangular region D or an empty set, see Fig. 4. Note that any friction model can be used in the above approach, as long as the estimated or measured value of µ at each time is not a function of the traction forces. But even if F₁ and F₂ influence the equivalent µ , e.g. for deformable terrain, this method can still be used. In this latter case, e.g., the terrain cohesion coefficient would simply turn the lines from e) and f) into sloped ones instead of vertical or horizontal. The region D would still be a polygon, not increasing too much the complexity of the proposed algorithm. However, for the sake of simplicity in the formulation presented below, the region D will be assumed as a rectangle.

To take into account measurement uncertainties, it is desirable to use, in practice, a subset of region D. This can be done, for instance, through the use of a safety factor sf greater than 1. The region D above would then be defined using a value of µ obtained from the current estimate of the friction coefficient divided by sf, resulting in a safety margin against wheel slippage. In addition, the values of F_sat1 and F_sat2 could be both divided in the equations above by sf to avoid working near motor saturation. Without loss of generality, the safety factor used in this work is 1.0.

Speed Control Law

One of the objectives of the proposed DRTC is to guarantee that the speed V_L of the robot's center of mass along the longitudinal direction to the chassis (measured in the global coordinate frame, see Fig. 5) is equal to a desired speed V_d, therefore it is desired that:

The longitudinal velocity V_L can be calculated at a time t_f from its value ºV_L at an initial instant t₀ and the acceleration a_L(t) of the center of mass in the longitudinal direction

The acceleration a_L can be controlled through the wheel torques which, in turn, control the wheel-terrain traction forces. Being it a first order system, as seen in Eq. (23), proportional control is satisfactory. Considering a proportional gain K_p for the error between the desired and actual longitudinal speeds, the following control law is proposed:

The acceleration a_L can be calculated from the center of mass acceleration components in the global frame x-y and the chassis angle α:

From Eqs. (9)-(10), the acceleration a_L can be written as a function of the traction forces F₁ and F₂ and of parameters η₁, η₂ and a₀, all of which are known for a given state, resulting in

where

Eqs. (24)-(26) then result in:

The values of F₁ and F₂ that satisfy the above equation will generate a straight line S in the F₁ × F₂ plane. This line represents all combinations of traction forces that are able to achieve a desired speed V_d. Thus, the intersection set Γ between the region D and the straight line S will return all possible combinations that, besides controlling the robot speed, satisfy all conditions from a) to f) described before, see Fig. 6 (top).

Note that the S line cannot be parallel to the F₁ or F₂ axes because η₁ and η₂ are always different than zero. But note that if cos(γ₁ - α) tends to 0, then the coefficient η₁ tends to infinity. This means that F₁ should be chosen as zero to satisfy Eq. (31). This unusual configuration would be associated with a back wheel traction force F₁ perpendicular to the direction of V_L. Analogously, if cos(γ₂ - α) tends to 0, then the coefficient η₂ tends to infinity and F₂ should be chosen as zero.

When Γ is an empty set (i.e. S does not cross region D), then the proposed technique won't be able to achieve the desired end without violating the conditions a) through f). However, these conditions are more important than the speed control since they're related to the system integrity. In this case, the control algorithm looks for the point P = (F₁, F₂) inside region D that will lead to the acceleration a_e closest to the desired value a_L from Eq. (24), see Fig. 6 (bottom). Since iso-acceleration lines in the F₁ × F₂ plane are always straight lines, as seen from Eq. (26), one of the vertices of the rectangle D will always be the closest point to the external iso-acceleration line associated with a_L. It is then enough to calculate the longitudinal accelerations associated to the four vertices of D, and choose the one closest to a_L, e.g. the point P in Fig. 6 (bottom).

On the other hand, if Γ is not empty, then it will be either a vertex from D or a straight line segment P₁-P₂, see Fig. 6 (top). In the latter case, there will be infinite points (F₁, F₂) Γ that could be chosen to control the robot's longitudinal velocity guaranteeing conditions a) through f). Another optimization criterion can then be used to choose a point in Γ. The minimization of the robot power consumption is chosen in this work, as described next.

Minimization of the System Power Consumption

The power dissipated by the wheel motors can be divided into two parts, one due to the mechanical output work at the motor shaft, and another due to power losses (such as in the Joule effect in DC motors). Assuming that the motor efficiency is high (e.g. a DC motor with low internal electric resistance and low no-load currents), then the second part is neglected, resulting in a total required power for both wheels:

The above expression assumes that the robot does not have regenerative braking, i.e., it does not recover energy from the braking process (which, however, would be possible when using DC motors, as the batteries could be recharged when T_i and ω_i have opposite signs).

Assuming no slip between the wheels and motor shafts (due to clutches, for example), and neglecting the wheel inertia, then T_i is equal to the traction force F_i multiplied by the wheel radius r. Also, assuming the proposed DRTC won't allow wheel slip, then, |ω_i| is equal to the speed |V_ci| of the center of wheel i divided by r. Equation (32) becomes

For a desired longitudinal speed V_d of the robot center of mass, the speeds of the wheel centers can be calculated by

From Eqs. (33)-(34), the total power required by the system is a function of the parameters

₁ and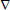 ₂, which are constant for a given system state and desired speed, and of the traction forces F₁ and F₂:

where

From Eq. (35), the locus of the points with same power in the F₁ × F₂ plane would have a diamond shape, centered at the origin. Therefore, the power consumption minimization problem could be geometrically regarded as finding the smallest of such diamonds that would intersect the segment Γ. Clearly, there are four basic cases: the intersection point that minimizes power could be point P₁, P₂, or the intersection of Γ with the F₁ axis or with the F₂ axis, see Fig. 7.

Note that if Γ is parallel to any side of the diamond, then there may be an infinite number of solutions. But, in any case, at least one of the solutions shown in Fig. 7 is valid. Thus, it is enough for the algorithm to calculate the power at points P₁, P₂, and at the intersection of Γ with the F₁ and F₂ axes (if it intersects either axis), choosing then the solution that results in minimum power. The resulting optimized F₁ and F₂ values are used to calculate the associated wheel torques, which are then commanded to the motors. In this way, the robot is able to control its speed in rough terrain while avoiding dynamic instabilities due to loss of wheel-terrain contact, avoiding slippage and considering motor saturation, as well as minimizing power consumption when possible. Figure 8 shows a flowchart summarizing the proposed method.

Recovering from Wheel-Terrain Contact Loss

Ascending rough terrain or very high forward accelerations may cause the loss of contact between the front wheel (or both front wheels for the 3D case) and the terrain. The same is true when braking or descending steep slopes, except for the back wheel(s). It is possible for the robot to recover from this event to avoid flip-over dynamic instability.

A very simple method to recover wheel-terrain contact is to use the torque from the wheel(s) that are still in contact to tilt the robot back in place. Therefore, if the robot loses contact of the back wheel(s), the front wheel(s) should accelerate. This has been experimentally verified with the first prototype of the Hybrid Environmental Robot, see Fig. 9. This figure shows the robot descending a very sloped terrain. If no control action is taken, the back wheels lose ground contact and the robot flips over. When the same experiment is repeated with the front wheels accelerating right after the back wheel contact loss, the robot is able to successfully recover. The same would be true for a loss contact of the front wheel(s), however in this case the control action would be to brake the back wheel(s), assuming the robot as moving forward.

Note, however, that the choice of the recovering traction force is still limited by the region D previously defined, to avoid slipping and to consider motor saturation. The speed control law and the power minimization equation cannot be applied during the recovery process, since only one wheel (in the 2D case) is in contact with the ground. The control action for front wheel contact loss is then to just apply the minimum value of the back wheel traction force F₁, obtained from the region D. On the other hand, in the event of back wheel contact loss, the maximum value of the front wheel traction force F₂ should be applied, within the region D as well. After the recovery has finished, DRTC is resumed. The detection of contact loss in the real system is not addressed in this work; however, it could be accomplished from an Extended Kalman Filter applied to the robot inertial sensors and wheel encoders, from force/torque sensors at the wheel shafts, or from special pressure sensors at the wheel rims. In the next section, the proposed approach is verified through simulations.

Simulation Results

Simulations are performed using real parameters taken from the second prototype of the Hybrid Environmental Robot (HER), namely m = 120 kg, I = 15.22 kg·m², F_sat1 = F_sat2 = 320 N, r = 0.3 m, L₁ = L₂ = 0.7 m, h₁ = h₂ = 0.425 m, K = 10⁵ N/m and c = 4.8·10³ kg/s. Also, g = 9.8 m/s², and the wheel-terrain friction coefficient is assumed as µ = 0.5.

The proposed Dynamic Rough Terrain Control (DRTC) is compared with traditional velocity control (TVC) with gravity compensation. TVC assumes that the terrain beneath the wheels is approximately flat, therefore the wheel-terrain contact angles are equal to the chassis angle, γ₁ = γ₂ = α. In this special case, Eq. (31) would become

Note that, on a flat terrain, only the sum of the traction forces F₁ and F₂ matters, not their individual values (as long as such values do not cause slippage, motor saturation or flip-over dynamic instability caused by loss of wheel contact, which are not modeled in TVC). TVC then evenly distributes the torque to both motors, resulting in the same traction forces F₁ and F₂. The TVC law with gravity compensation is then

Note that the same proportional gain K_p is used here for both DRTC and TVC, to provide a fair comparison between them. In fact, from Eqs. (37)-(38) it can be seen that both control techniques should result in the same response for flat terrains with small slopes.

Figure 10 shows the terrain profiles considered in the simulations. All simulations assume zero initial robot velocity.

Flat Terrain Simulation Results

For the flat terrain simulation from Fig. 10(a), the proportional gain K_p = 2.45 s^-1 is used for both DRTC and TVC. This gain value is appropriate for several terrains with average 30º slopes. Higher values could be used without compromising the validity of the simulations, because motor saturation is included in the model. The results for flat terrain simulations are shown in Figs. 11 to 14.

Figure 11 shows the robot's longitudinal speed from DRTC and TVC.

As expected for flat terrain, both control techniques achieve the desired speed V_d = 1 m/s in approximately 2 s. This figure also shows the similar power requirements of both control methodologies. At steady state, after the initial acceleration period, both control techniques converge to a power consumption of approximately 231 W.

The absolute values of the ratios between the traction and normal forces at each wheel are shown in Fig. 12 for both controls. DRTC is able to apply large forces F₂ to the front wheel in the beginning of the simulation; however, still avoiding slippage as the ratio |F₂|/N₂ is kept lower than the static coefficient of friction µ = 0.5.

The proposed control also takes advantage of the increased normal N₁ of the back wheel due to dynamic effects during the robot acceleration, delivering large F₁ forces as well. TVC, on the other hand, does not model dynamic effects nor takes into account the possibility of slippage, resulting in a more conservative approach that slows down the system response.

TVC allows slippage of the front wheel in the very beginning of the simulation, as it can be seen from the ratio between the desired traction force F₂ and the normal N₂ reaching 0.64, higher than µ . Note also that at steady state, TVC does not take advantage of the higher normal force N₁ at the rear wheel, caused by the ascending slope of the terrain, resulting in |F₁|/N₁ < |F₂|/N₂. This can also be seen in Fig. 13, which shows the values of F₁ and F₂. Note that TVC always considers F₁ = F₂, failing to take advantage of dynamic and gravity effects that cause in general N₁ N₂.

The resulting normal forces from the flat terrain simulation are shown in Fig. 14. Note that even under steady state the rear wheel always sees a normal force N₁ larger than the N₂ from the front one, because of the ascending slope of the terrain. In addition, in the first seconds of the simulation, when the robot is accelerating, it can be noticed an increase in N₁ and reduction in N₂ due to dynamic effects. As expected, both DRTC and TVC result in the same normal forces. This happens because on flat terrain F₁ and F₂ are always parallel and decoupled from N₁ and N₂, therefore their sum is the same for DRTC and for TVC.

Sinusoidal Terrain Simulation Results

The results for the simulation on the sinusoidal terrain from Fig. 10(b) are shown in Figs. 15 to 18. Figure 15 shows the robot longitudinal speed from DRTC and TVC.

The simulation parameters are the same as those from the flat terrain case. Both methodologies are able to converge to the desired speed V_d = 1 m/s in approximately 2 s, without significant oscillations.

After 3 s, however, it is found that the wheel-terrain friction coefficient is not large enough to enable either control to maintain the desired speed. DRTC is able to recover after this period, as opposed to TVC. Note that even gravity compensation is not enough in TVC to control the velocity, because of the hypothesis of flat terrain (γ₁ = γ₂ = α) used in this compensation. Indeed, it can be clearly seen in Fig. 6 that the slope α of the robot chassis can be very different from the wheel-terrain contact angles γ₁ and γ₂ as the vehicle moves along the wavy path.

Figure 15 also shows the power requirements of each control method. It is seen that the proposed DRTC is able to always keep the power below 1,000 W while avoiding wheel slip. TVC, on the other hand, leads to a 2,200 W peak.

The values of the desired ratios |F_i|/N_i at each wheel (i = 1, 2) are shown in Fig. 16 for both simulated control methods. DRTC is able to efficiently explore the upper limit of these ratios, which is the static coefficient of friction µ = 0.5. Note how the values of the ratios sometimes switch between front and real wheels. This is a result of the power minimization addressed by the proposed algorithm, choosing which motor is more efficient to deliver higher torques depending on the current values of γ₁, γ₂ and α. This can also be seen in Fig. 17 (top), which shows the values of F₁ and F₂. Note that on real systems such switching may be slightly delayed due to, e.g., the DC motor inductance; however, current high-end motors and electronics are able to deliver a quite high frequency response. TVC, on the other hand, does not make such switches, because it always considers F₁ = F₂, as seen in Fig. 17 (bottom). Because of that, both wheels end up slipping as seen in Fig. 16 (bottom) from the desired |F_i|/N_i ratios higher than 0.5 during most of the TVC simulation.

Figure 18 shows that DRTC results in a smoother movement than TVC, because the latter has a much steeper variation in normal forces. In addition, the minimum normal forces from DRTC along the path are higher than the TVC minimum values, resulting in a greater stability margin against flip-over.

Very Steep Terrain Simulation Results

The results for the simulation on the very steep sinusoidal terrain from Fig. 10(c), which is described by the equation f(x) = 2·sen(0.4x), are shown in Figs. 19 and 20. This terrain was chosen in such a way that at its steepest point the robot would flip over if climbing in a quasi-static manner. Therefore, only dynamically it is possible to be traversed, actively controlling the traction forces to guarantee normal forces greater than zero in all wheels.

It can be seen from Fig. 19 that TVC would lead to flip over when climbing uphill, as the front wheel normal force drops to zero after about 1.3 s. This simulation was stopped when the robot chassis angle γ resulted in a value larger than 90º. With DRTC, on the other hand, the robot is able to traverse this very steep terrain without wheel contact loss, as seen in Fig. 20.

Rough Terrain Simulation Results

The results for the simulations on the rough terrain from Fig. 10(d) are shown in Figs. 21 to 23.

From Fig. 21 it can be seen that DRTC is able to converge to the desired speed of 0.5 m/s in about 1s, with very small oscillations afterwards. TVC is not able to control the system, due to terrain roughness, even though it spends an approximately equal amount of average power as DRTC.

The values of the desired ratios |F_i|/N_i at each wheel (i = 1, 2) are shown in Fig. 22 for both simulated control methods. DRTC is able to always keep these ratios below the static coefficient of friction between the tires and the soil (assumed in this simulation µ = 0.5). In practice, the value of µ used in the control should be a lower bound of the estimated coefficient of friction, in order to keep a safety margin against sliding. TVC would result in sliding, as seen in Fig. 22 (bottom) from the |F_i|/N_i ratios reaching values above µ . Note that the sudden changes in the |F_i|/N_i ratios shown in Fig. 22 (bottom) are due to the assumption that the wheel motors have a very fast actuation response.

The traction forces for both methodologies are shown in Fig. 23. Note that DRTC considers motor saturation, as both traction forces do not exceed F_sat1 = F_sat2 = 320 N. Also, at several moments one of the motors is switched off by DRTC, minimizing power consumption and avoiding low normal forces that might lead to wheel contact loss. It is found that the minimum value of the normal force N₂ along such rough terrain path using DRTC is N_2,min = 360 N, much larger than TVC's N_2,min = 180 N, resulting in a much larger stability margin. Indeed, further simulations in such terrain for a higher desired speed of 2 m/s result in wheel contact loss for TVC, while DRTC is able to maintain all normal forces positive during the entire simulation.

Conclusions and Future Work

In this work, a novel traction control method was proposed to achieve desired speeds in rough terrain, taking into account motor saturation while guaranteeing dynamic stability and avoiding wheel slippage. When possible, power consumption was also minimized. The method is based on a computed torque control scheme that explicitly considers the different contact angles at each wheel and the dynamic interaction between the vehicle and the terrain, optimized to minimize power consumption. The main contribution of this method comes from the fact that it has a closed-form analytical solution for the optimized 2D approach, which allows for a fast control implementation even in mobile robots with limited hardware. In addition, this method is not limited to flat or uneven terrain, where the terrain gradient is assumed constant along the vehicle footprint; the proposed approach can deal even with very rough terrain, where different tire/soil contact angles among the wheels must be considered.

Simulations demonstrated the effectiveness of the proposed traction control for flat, uneven, very steep, and rough terrain, managing to reach the desired speeds much faster than traditional velocity control techniques with gravity compensation under similar conditions. The technique can also be applied to high speed systems, as long as the terrain is not too rough to make it impossible to maintain ground contact. Note, however, that brief losses of ground contact can be tolerated by the proposed control. The proposed approach converges with low power requirements even for very rough terrain, where traditional techniques aren't able to effectively control the robot speed. The presented equations can be either applied as a feedforward control, if the terrain profile is known beforehand, or as a feedback loop, if the wheel-terrain contact angles are estimated online from robot sensors and, e.g., Extended Kalman filters.

The proposed approach can be extended to the 3D case; however, the control law would not have a closed-form analytical solution, which is the greatest advantage of the presented 2D approach. Such 2D approach can be applied as well to real (3D) robots, as long as the chassis roll angles do not vary too much at the considered terrain. The general 3D approach implies in a substantial increase in the algorithm complexity. The friction model between the wheel and the terrain will need to deal with both longitudinal and transversal forces. For tank steering robots such as HER, the control will try to avoid slip in the longitudinal direction; however, it will allow slip in the transverse direction to promote steering. The coupling between longitudinal and transverse friction forces will need to be considered, using e.g. the friction ellipse concept.

The implementation of the proposed method in the HER prototype is currently under development. HER, which is equipped with Garmin GPS sensors and an Xsens inertial sensor, uses a PC-104 embedded computer system running on Linux. The control software is written in the C++ language, allowing control frequencies of over 1 kHz. Since the control algorithm has a closed form solution, its calculation on a typical computer system lasts only a few microseconds, not causing any control delay.

Future work could include the wheel inertia in the model, motor non-linearities for better calculations of power minimization, and wheel-terrain friction non-linearities. However, these improved models would require numerical methods to calculate the control law output. Techniques to generate a 3D terrain map based on stereo vision could also be studied, to improve the estimation of the wheel-terrain contact angles

Acknowledgements

The authors would like to thank Eng. Ney Robinson Salvi dos Reis, from CENPES/PETROBRAS, for all the provided information on the Hybrid Environmental Robot, and the support from ANP and CNPq for the scholarships of Alexandre Silva and Auderi Santos.

Paper accepted April, 2010.

Technical Editor: Glauco A. de P. Caurin.

References

• Albagul, A., Wahyudi, 2004, "Dynamic Modelling and Adaptive Traction Control for Mobile Robots", International Journal of Advanced Robotic Systems, Vol. 1, No. 3, pp. 149-154.
• Anwar, S., 2003, "Brake-Based Vehicle Traction Control via Generalized Predictive Algorithm", SAE International, USA.
• Balaram, J., 2000, "Kinematic state estimation for a Mars Rover", Robotica, Vol. 18, pp. 251-262.
• Burg, J., Blazevic, P., 1997, "Anti-Lock Braking and Traction Control Concept for All-Terrain Robotic Vehicles", in IEEE International Conference on Robotics and Automation, Albuquerque, USA.
• Caltabiano, D., Ciancitto, D. and Muscato, G., 2004, "Experimental Results on a Traction Control Algorithm for Mobile Robots in Volcano Environment", in IEEE Int. Conference on Robotics and Automation, New Orleans, USA.
• Caltabiano, D., Muscato, G., 2002, "A Comparison Between Different Traction control Methods For a Field Robot", in International Conference on Intelligent Robots and Systems, IEEE, Lausanne, Switzerland.
• Chatila, R., Andrade, G., Lacroix, S., Mallet, A., Medeiros, A.A.D., 1999, "Motion Control for a Planetary Rover", in International Conference on Field and Service Robotics, Vol. 1, pp. 381-388, Pittsburgh, USA.
• Grand, Ch., BenAmar, F., Plumet, F., Bidaud, Ph., 2004, "Decoupled control of posture and trajectory of the hybrid wheel-legged robot Hylos", in IEEE International Conference on Robotics & Automation, New Orleans, USA.
• Iagnemma, K., Dubowsky, S., 2004, "Mobile Robot in Rough Terrain: Estimation, Motion Planning, and Control with Application to Planetary Rovers", Berlin: Springer, 110 p.
• Krebs, A., Thueer, T., Carrasco, E., Siegwart, R., 2008, "Towards torque control of the CRAB rover", Proc. of the 9^th International Symposium on Artificial Intelligence, Robotics and Automation in Space (iSAIRAS).
• Lamon, P., Siegwart, R., 2005, "Wheel Torque Control in Rough Terrain: Modeling and Simulation", in IEEE International Conference on Robotics and Automation, Barcelona, Spain.
• Sakai, S., Sado, H. and Hori, Y., 1999, "Motion Control in an Electric Vehicle with Four Independently Driven In-Wheel Motors", IEEE/ASME Transactions on Mechatronics, Vol. 4, No. 1, pp. 9-16.
• Santos, A.V., 2007, "Projeto e Controle de Estabilidade de um Sistema Robótico Anfíbio para Sensoriamento Remoto", M.Sc. Thesis, Mech. Eng. Dept., Pontifical Catholic University of Rio de Janeiro, Brazil, 120 p. (In Portuguese).
• Sarkar, N., Yun, X., 1998, "Traction Control of Wheeled Vehicles Using Dynamic Feedback Approach", in IEEE International Conference on Intelligent Robots and Systems, Victoria, Canada.
• Silva, A.F.B., 2007, "Modelagem de Sistemas Robóticos Móveis para Controle de Tração em Terrenos Acidentados", M.Sc. Thesis, Mech. Eng. Dept., Pontifical Catholic University of Rio de Janeiro, Brazil, 126 p. (In Portuguese).
• Silva, A.F.B., Santos, A.V., Reis, N.R.S., Meggiolaro, M.A., 2008, "Traction Control of All-Wheel-Drive Independent Suspension Mobile Robots in 2D Rough Terrain", in ABCM Symposium Series in Mechatronics Vol. 3, Editor: P.E. Miyagi, Journal of the Brazilian Society of Mechanical Sciences and Engineering, Rio de Janeiro, Brazil, pp. 256-265.
• Simeón, T., Dacre-Wright, B., 1993, "A Practical Motion Planner for All-terrain Mobile Robots", in IEEE International Conference on Intelligent Robots and Systems, Yokohama, Japan.
• Tarokh, M., McDermott, G., Hayati, S., Hung, J., 1999, "Kinematic Modeling of a High Mobility Mars Rover", in IEEE International Conference in Robotics & Automation, Detroit, USA.
• Thueer, T., Krebs, A., Lamon, P., Siegwart, R., 2007, "Performance Comparison of Rough-Terrain Robots - Simulation and Hardware", Journal of Field Robotics, Vol. 24, No. 3, pp. 251-271.

Publication Dates

• Publication in this collection
  07 Jan 2011
• Date of issue
  Dec 2010

History

• Received
  Apr 2010