Application of SAC-SMA and IPH II hydrological models in the Teles Pires River basin, Brazil

Aplicação dos modelos hidrológicos SAC-SMA e IPH II na bacia do rio Teles Pires, Brasil

ABSTRACT

Parameterization and performance analysis of a hydrological model allow its consolidation, so that water-resource management strategies could be evaluated and extreme events forecast. In this context, this study aimed to evaluate the performance of the Sacramento Soil Moisture Accounting (SAC-SMA) and IPH II models for runoff estimation in the Teles Pires River basin, which is located in the Amazon region, State of Mato Grosso, Brazil. Both models were automatically calibrated using Shuffled Complex Evolution algorithm (SCE-UA) and validated for five runoff monitoring units. Our results showed that both are suitable for daily runoff modeling in the Teles Pires River basin with higher performance in larger drainage area basins. We can also infer that the simple use of complex rainfall-runoff models might not provide improved estimates. Although the SAC-SMA is the most complex and detailed model for hydrological processes, it has not outperformed IPH II in any of the monitoring units in the Teles Pires River.

Keywords:  Rainfall-runoff; Concentrated models; Planning of water resources; Runoff forecast

RESUMO

A parametrização e a análise do desempenho de um modelo hidrológico permitem sua consolidação para avaliação de estratégias de gerenciamento de recursos hídricos e para previsão de eventos extremos. Nesse contexto, o objetivo do trabalho foi avaliar o desempenho dos modelos chuva-vazão Soil Moisture Accounting (SAC-SMA) e IPH II para predição de vazões na bacia do rio Teles Pires, localizada na região amazônica do estado de Mato Grosso, Brasil. Os modelos foram calibrados de forma automática com o algoritmo Shuffled Complex Evolution (SCE-UA) e validados para cinco seções de monitoramento de vazão. Os resultados mostraram que ambos os modelos são adequados na modelagem de vazões diárias na bacia do rio Teles Pires e que apresentam melhor desempenho para estimativa de vazões em bacias com maior área de drenagem. Além disso, conclui-se que a complexidade de um modelo hidrológico chuva-vazão não é necessariamente sinônimo de melhores estimativas. Apesar de o modelo SAC-SMA ser mais complexo e apresentar maior detalhamento dos processos hidrológicos, ele não conseguiu superar o desempenho do IPH II em todas as seções de monitoramento de vazão do rio Teles Pires.

Palavras-chave:  Chuva-vazão; Modelo concentrado; Planejamento de recursos hídricos; Previsão de vazão

INTRODUCTION

Hydrological models can be used to obtain different information, necessary to support the decision making in the planning of water resources because they allow to represent the behavior of hydrological phenomena that occur in a river basin ( DEVIA; GANASRI; DWARAKISH, 2015 ; MELLO et al., 2016 ; PECHLIVANIDIS et al., 2011 ).

In order to be used operationally, the hydrological model must present adequate performance for runoff forecasting, which can be used by the electric sector for reservoir management and elaboration of the hydroelectric plant operation program, by management bodies for simulation of water resource planning scenarios, as well as to mitigate the impacts caused by extreme outflows ( TUCCI, 2005 ; TUCCI; CLARKE; COLLISCHONN, 2003 ).

In the electric sector, power generation in hydroelectric plants depends on the storage of water in the reservoir and on the prediction of affluent flows with a horizon that reaches 14 days, among other variables. This runoff forecast allows the use of different models of operation, optimization and energy simulation to evaluate the operational conditions of the plants. In addition, it allows decision-making to mitigate the impacts resulting from extreme inflows to the reservoir ( GOMES; MONTENEGRO; VALENÇA, 2010 ; OLIVEIRA; LIMA, 2016 ).

Based on climatic projections, hydrological simulation allows quantifying water availability in different scenarios, minimizing the impact of climate uncertainties on water resources management, as discussed by Huang, Kadir and Chung (2012) , Koutroulis et al. (2013) , Nóbrega et al. (2011) and Vaze et al. (2010) .

According to Viola et al. (2009) , hydrological simulation in basins under intensive agricultural production represents an important tool for the management of water resources, mainly for the characterization of the runoff that can be granted for irrigation projects.

In the specific case of the Teles Pires River basin, hydrological modeling assumes even greater importance, since the region is among the 16 main national centers of center pivot irrigation and has the potential to increase the irrigated area, according to the National Water Agency ( ANA, 2016) .

In addition to the irrigated area, the Teles Pires River Basin has the potential to generate electricity of approximately 3,697.0 MW, in six hydroelectric plants ( EPE, 2009 ), which requires even more extreme weather forecasting for reservoir management.

Before use, rainfall-runoff models need to be calibrated and validated, depending on the characteristics of the river basin.

Calibration consists of a cause-and-effect process where the system attempts to abstract from the input data the information required to assess which parameter values will make the model reproduce properly the natural system. However, the validation allows to confirm the accuracy of the model, aiming at the simulation of stationary processes in the hydrographic basin ( ANDRADE; MELLO; BESKOW, 2013 ; ARABI; GOVINDARAJU; HANTUSH, 2006 ; MAGALHÃES, 1989 ).

There are a large number of hydrological models, with unique characteristics and specific applications in water resource engineering ( DEVIA; GANASRI; DWARAKISH, 2015 ). Among the several hydrological models, the present study evaluated IPH II ( TUCCI, 2005 ) and SAC-SMA ( BURNASH, 1995 ), which were selected because they essentially require as input data the mean rainfall and evapotranspiration, which can be obtained for most of the Brazilian river basins; they have no limitations on the characteristics of the basins (area, vegetation, geology, characteristics of the drainage channel, among others); present great potential of use in Brazilian river basins; and still be poorly explored in Brazil, especially the SAC-SMA.

The IPH II model is a simple model with only seven parameters and can be used in basins with different characteristics. The model was used in studies such as that of Bertoni, Tucci and Clarke (1992) , Brun and Tucci (2001) , Mine and Tucci (1999) and Pereira et al. (2016a) for estimating runoff in watercourses. Both authors concluded that the model has adequate performance for estimating river runoff and can be used to predict the affluent volume to hydroelectric reservoirs, as well as for decision-making in matters related to water resources management.

The conceptual Soil Moisture Accounting (SAC-SMA) model, also known as Sacramento, is considered complex, has thirteen parameters and was initially developed to forecast flood events in the Sacramento River, located in the United States. Due to its excellent runoff forecasting performance, it has been used by the United States National Weather Service (NWS-NOAA) and several other countries for this purpose ( ANDREWS; CROKE; JAKEMAN, 2011 ; BOUGHTON, 2005 ).

Studies such as Koutroulis et al. (2013) , carried out in 15 river basins of Greece, and Breda, Gonçalves and Silveira (2011) for the Brazilian river basin of the Iguaçu River, show that the SAC-SMA model has adequate performance for estimating runoff in watercourses.

In this context, the goal of this study was to check the performance of the rainfall-runoff models SAC-SMA and IPH II for the daily runoff estimation of the Teles Pires River basin, so that they can be used by the electric sector, users of water and by the public authority for the planning and management of water resources in the river basin.

MATERIAL AND METHODS

Study area

The study area corresponds to the Teles Pires River basin, with a drainage area of 81,748.1 km², located in the Amazon region of the State of Mato Grosso, Brazil ( Figure 1 ). For hydrological modeling, the study area was divided into five sub-basins; the outfall was the location of the fluviometric stations of the national hydrometeorological network.

Figure 1
Location of the Teles Pires River basin and the stations used in the study.

Table 1 lists the information of the fluviometric, pluviometric and weather stations, belonging to the national hydrometeorological network, used in the study. Figure 1 illustrates the location of these stations.

Table 1
Fluviometric, pluviometric and weather stations, used in the study.

ID	Code	Name	Station	Lat.	Long.
1	1720000	Porto Roncador	F	-13.55	-55.33
2	1721000	TelesPires	F	-12.67	-55.79
3	1728000	Cachoeirão	F	-11.65	-55.7
4	1730000	FazendaTratex	F	-10.95	-55.54
5	1738000	Jusante Foz P. de Azev.	F	-9.65	-56.01
6	1453000	Passagem da BR-309	P	-14.61	-53.99
7	1454000	Paranatinga	P	-14.41	-54.04
8	1356002	Nova Mutum	P	-13.81	-56.12
9	1355001	Porto Roncador	P	-13.55	-55.33
10	1255001	TelesPires	P	-12.67	-55.79
11	1255002	Rio Ferro	P	-12.51	-54.91
12	1154001	Santa Felicidade	P	-11.92	-54.99
13	1055003	FazendaTratex	P	-10.95	-55.54
14	1055002	Colíder	P	-10.79	-55.44
15	1054000	AgropecuáriaCajabi	P	-10.74	-54.54
16	1055001	Indeco	P	-10.11	-55.57
17	0956000	Alta Floresta	P	-9.87	-56.10
18	0954001	Cachimbo	P	-9.81	-54.88
19	0956001	Foz P. de Azevedo	P	-9.64	-56.01
20	83214	Matupá	M	-10.25	-54.91

• ID = identification of the station on the map in Figure 1 ; Code = code of the national hydrometeorological network; F = fluviometric station; P = pluviometric station; M = weather station; Lat. = Latitude (°); Long. = Longitude (º).

Regarding the characteristics of the relief, for the sub-basins of the monitoring units 17380000, 17300000, 17280000, 17210000 and 17200000, it was observed a maximum altitude of 893 m and a minimum of 226 m, 259 m, 301 m, 322 m and 349 m, respectively. With the hypsometric curves, the variation of the relief of the sub-basins is relatively small, confirming the fact that the region is relatively flat and consequently there are no great variations between the altitudes and their respective drainage areas ( WENZEL et al., 2017 ). According to the authors, the average altitudes calculated for the sub-basins 17380000, 17300000, 17280000, 17210000 and 17200000 were 371 m, 412 m, 421 m, 455.6 m and 472 m, respectively.

When analyzing the average slopes of the drainage areas of the Teles Pires River, Wenzel et al. (2017) found that most of the sub-basin slopes vary from 0 to 1%, concluding that they fall into flat relief. Other information related to the physiographic characteristics of the sub-basins used in this study can be consulted in the research of these authors.

Input data for hydrological models

The IPH-II and Sacramento (SAC-SMA) models require the reference evapotranspiration and the mean rainfall of the basin as input variables.

The daily reference evapotranspiration (ET₀) was calculated by the Camargo method, using Equation 1 . The availability of the maximum and minimum temperature data in the period was determinant for the choice of ET₀ calculation by this method. According to Tanaka et al. (2016) , when only air temperature data are available, the ET₀ estimation model recommended for the Teles Pires River basin region is that of Camargo ( Equation 1 ).

${\text{ET}}_{\text{0}}{\text{=F×H}}_{\text{0}}{\text{×T}}_{\text{med}}$ (1)

where: ET₀ is the reference evapotranspiration (mm day^-1); F is the adjustment factor, which varies with the average annual air temperature (Ta) - the value of F was equal to 0.011 for Ta = 25 °C; H₀ is the extraterrestrial radiation in equivalent evaporation (mm day^-1); T_med is the average daily temperature (°C).

The average daily rainfall of the sub-basins with control units at the fluviometric stations of Porto Roncador (1), Teles Pires (2) and Cachoeirão (3) were obtained by the Thiessen method, as described by Macêdo et al. (2013) , according to Equation 2 . This method takes into consideration the geometry of the pluviometric stations location plan to consider the influence of their data on the calculation of average rainfall in the drainage area. In the sub-basins with control units at the fluviometric stations Fazenda Tratex (4) and Jusante Foz Peixoto de Azevedo (5), the average rainfall was obtained using the arithmetic mean method by means of Equation 3 .

$\overline{P}=\frac{{{\displaystyle \sum }}_{i=1}^n{P}_i{A}_i}{A_t}$ (2)

in which: A_i is the area of influence (km²) of the pluviometric station i with rainfall P_i(mm); A_t is the total area (km²) of the basin.

$\overline{P}=\frac{{{\displaystyle \sum }}_{i=1}^n{P}_i}{n}$ (3)

in which P_i (mm) is the average rainfall of the measurements of the rain gauges installed in the basin; n is the total number of rain gauges.

IPH II hydrological model

The automatic calibration of the IPH II model and runoff estimates were calculated using the WIN-IPH2 software developed by Bravo et al. (2006) . For automatic calibration of the IPH II hydrological model, the Shuffled Complex Evolution algorithm (SCE-UA) developed by Duan et al. (1992) was used.

Figure 2 illustrates a schematic representation of the main activities performed to estimate the daily runoff with the IPH II model. Detailed descriptions of the IPH II hydrological model can be obtained in Tucci (2005) .

Figure 2
Schematic representation with the main activities performed for runoff estimation using the IPH II model.

The data periods of the historical series of runoff, rainfall and evapotranspiration used in the calibration and validation stages can be observed in Table 2 , as well as the objective function used in the calibration with the SCE-UA algorithm and the drainage area of the Teles Pires River sub-basins.

Table 2
Objective function (OF), period of the data used in the calibration and validation stages of the IPH II model and the drainage area (km²) of the Teles Pires River sub-basins.

Station	OF	Calibration	Validation	Area
1720000	MAE	Aug./2000 to Dec./2008	Jul./1998 to Jul./2000	10,823.31
1721000	MAE	Jun./1998 to Dec./2003	May/2005 to Dec./2008	14,030.98
1728000	MAE	May/1998 to Dec./2001	May/2005 to Dec./2008	34,689.68
1730000	ENS	May/1998 to Dec./2003	May/2007 to Dec./2008	40,812.78
1738000	ENS	May/1998 to Dec./2004	May/2007 to Dec./2008	81,748.27

• MAE = mean absolute error; E_NS = Nash-Sutcliffe efficiency index.

For calibration and validation of the IPH II model, the “Split-Sample Test” methodology described by Klemes (1986) was used. According to this methodology, the historical records of rainfall and runoff should be divided into two segments, one of which should be used for calibration and the other for validation. The model was considered adequate when errors in both runs were acceptable.

The division of the historical series in half was not sufficient to adequately calibrate the parameters in most of the control units of the Teles Pires River due to the size of the historical series without missing data. Therefore, following a recommendation from the same author, a longer period was used for calibration and a shorter period for validation. In some historical series this longer period without missing data was the most recent, case of section 1720000-Porto Roncador ( Table 2 )

During the calibration of the hydrological model, different objective functions (OFs) were evaluated and those that provided the least error of estimation of the hydrological model in this stage were selected. These OFs are presented in Table 2 .

Table 3 lists the variation ranges of IPH II model parameters used in automatic calibration.

Table 3
Parameters of the IPH II model and variation range used in the calibration.

Parameter	Unit	Range
		Lower limit	Upper limit
I0	mm day-1	10.0	300.0
Ib	mm day-1	0.10	10.00
h	dimensionless	0.01	0.999
Ks	day	0.01	30.00
Ksub	day	0.10	500.0
Rmáx	mm	0.00	20.00
alfa	dimensionless	0.01	20.00

• I₀ is the initial infiltration capacity of the soil; I_b is the infiltration capacity of the soil when saturated; h = e^(-k), in which k is an empirical parameter related to the soil type; K_s is the average time for emptying the surface reservoir; K_sub is the average time for emptying the underground reservoir; R_máx is the maximum rainfall that can be retained by the interception reservoir (vegetation cover and soil depressions); alfa is a parameter of the model, related to a coefficient that represents the percentage of rainfall that flows on the surface.

SAC-SMA (Sacramento) hydrological model

Figure 3 shows the schematic representation of the SAC-SMA model. Detailed descriptions of this model, according to hydrological concepts, can be obtained in Burnash and Ferral (1996) .

Figure 3
Schematic representation of the SAC-SMA model, explaining the optimizable parameters. Source: Adapted from Van Werkhoven et al. (2009) .

The automatic calibration of the SAC-SMA model and the simulations were performed using an algorithm, implemented in R programming language, called Hydromad ( ANDREWS; CROKE; JAKEMAN, 2011 ).

The Shuffled Complex Evolution algorithm (SCE-UA) was used for automatic calibration of the model. Table 4 lists the data periods of the historical series of runoff, rainfall and evapotranspiration used in the calibration and validation steps of the SAC-SMA, the objective function used in the calibration with the SCE-UA, and the drainage area of the Teles Pires River sub-basins.

Table 4
Objective function (OF), period of the data used in the calibration and validation stages of the SAC-SMA model and the drainage area (km²) of the Teles Pires River sub-basins.

Station	OF	Calibration	Validation	Area
1720000	r.sq.sqrt	Aug./2000 to Dec./2008	Jul./1998 to Jul./2000	10,823.31
1721000	r.sq.sqrt	Jun./1998 to Dec./2003	May/2005 to Dec./2008	14,030.98
1728000	r.sq.sqrt	May/1998 to Dec./2001	May/2005 to Dec./2008	34,689.68
1730000	r.sq.log	May/1998 to Dec./2003	May/2007 to Dec./2008	40,812.78
1738000	r.sq.sqrt	May/1998 to Dec./2004	May/2007 to Dec./2008	81,748.27

• r.sq.sqrt = coefficient of determination calculated with the square root of the runoff data; r.sq.log = coefficient of determination calculated with logarithm of runoff data.

The objective functions and calibration and validation periods of the SAC-SMA model ( Table 4 ) were established following the same criteria used for the IPH II described above.

Table 5 presents the parameters of the SAC-SMA model and their respective ranges, proposed by Andrews et al. (2011) and Shin et al. (2013) .

Table 5
Parameters of the SAC-SMA (Sacramento) model and variation range according to Andrews et al. (2011) and Shin et al. (2013) .

Parameter	Unit	Range
		Lower limit	Upper limit
UZTWM	mm	1.00	150.00
UZFWM	mm	1.00	150.00
UZK	day-1	0.10	0.50
PCTIM	km2/km2	1.00E-06	0.10
ADIMP	km2/km2	0.00	0.40
ZPERC	dimensionless	1.00	250.00
REXP	dimensionless	0.00	5.00
LZTWM	mm	1.00	500.00
LZFSM	mm	1.00	1.000.00
LZFPM	mm	1.00	1.000.00
LZSK	day-1	0.01	0.25
LZPK	day-1	1.00E-04	0.25
PFREE	mm/mm	0.00	0.60

• UZTWM = upper zone tension water maximum capacity (mm); UZFWM = upper zone free water maximum capacity (mm); LZTWM = lower zone tension water maximum capacity (mm); LZFPM = lower zone primary free water maximum capacity (mm); LZFSM = lower zone supplemental free water maximum capacity (mm); UZK = upper zone free water lateral depletion rate (day^-1); LZPK = lower zone primary free water depletion rate(day ^-1); LZSK = lower zone supplementary free water depletion rate (day^-1 ); PCTIM = fraction of the impervious area (km²/km² ); ADIMP = fraction of the additional impervious area (km²/km² ); PFREE = direct percolation fraction from upper to lower zone free water storage (mm/mm); ZPERC = maximum percolation rate coefficient (none); REXP = exponent of the percolation equation (none).

Performance of hydrological models

In order to verify the performance of the IPH II and SAC-SMA models in the estimation of the runoff of the Teles Pires River Basin, the results obtained by the models were compared with the data observed in the five monitoring units using the following statistical measures: mean absolute error (MAE); root mean square error (RMSE); bias; paired t-test at 5% significance; Willmott's concordance index; and the Nash-Sutcliffe efficiency index (E_NS), respectively, obtained by:

$\text{MAE=}\frac{\text{1}}{\text{N}}{\displaystyle \sum }_{\text{i=1}}^{\text{n}}\left|{\text{O}}_{\text{i}}{\text{-P}}_{\text{i}}\right|$ (4)

$\text{RMSE=}{\left[\frac{\text{1}}{\text{N}}{\displaystyle \sum }_{\text{i=1}}^{\text{n}}{\left({\text{O}}_{\text{i}}{\text{-P}}_{\text{i}}\right)}^{\text{2}}\right]}^{\text{0}\text{.5}}$ (5)

$\text{bias=}\frac{\text{1}}{\text{N}}{\displaystyle \sum }_{\text{i=1}}^{\text{n}}\left({\text{O}}_{\text{i}}{\text{-P}}_{\text{i}}\right)$ (6)

$$\text{t=}\sqrt{\left[\frac{\left(\text{n-1}\right){\text{bias}}^{\text{2}}}{{\text{RMSE}}^{\text{2}}{\text{-bias}}^{\text{2}}}\right]}$$ (7)

$\text{d=1-}\frac{{{\displaystyle \sum }}_{\text{i=1}}^{\text{n}}{\left({\text{P}}_{\text{i}}{\text{-O}}_{\text{i}}\right)}^{\text{2}}}{{{\displaystyle \sum }}_{\text{i=1}}^{\text{n}}{\left(\left|{\text{P}}_{\text{i}}\text{-O}\right|\text{+}\left|{\text{O}}_{\text{i}}\text{-O}\right|\right)}^{\text{2}}}$ (8)

${\text{E}}_{\text{NS}}\text{=1-}\frac{{{\displaystyle \sum }}_{\text{i=1}}^{\text{n}}{\left({\text{O}}_{\text{i}}{\text{-P}}_{\text{i}}\right)}^{\text{2}}}{{{\displaystyle \sum }}_{\text{i=1}}^{\text{n}}{\left({\text{O}}_{\text{i}}\text{-O}\right)}^{\text{2}}}$ (9)

where P_i is the estimated runoff (m³ s^-1); O_i , is the observed runoff (m³ s^-1); O, is the mean of observed runoff values (m³ s^-1); and n, is the number of sample values.

To evaluate the performance of the models with respect to the Nash-Sutcliffe efficiency index (E_NS), the classification suggested by Van Liew et al. (2007) was adopted.

A detailed description of these statistical indices ( Equations 4 to 9 ) and interpretation thereof can be found in Uliana (2016) .

RESULTS AND DISCUSSION

IPH-II model

The value of the objective function (OF) and the parameters of the IPH II model automatically calibrated for each Teles Pires River sub-basin ( Figure 1 and Table 1 ) are presented in Table 6 . It can be seen in this Table that the optimization with the SCE-UA algorithm was effective since adequate OF values were obtained.

Table 6
Value of the objective function (OF) and parameters of the IPH-II model obtained by automatic calibration with the SCE-UA algorithm.

Parameter	Fluviometric station
	1	2	3	4	5
Io (mm d-1)	257.80	91.70	21.95	20.91	150.88
Ib (mm d-1)	0.78	1.60	4.04	2.27	2.77
h	0.17	0.61	0.55	0.99	0.73
Ks (d)	24.51	25.00	25.00	27.31	20.00
Ksub (d)	499.99	155.00	224.94	1.00	10.10
Rmáx (mm)	8.72	0.58	5.00	15.56	6.92
alfa	1.27	0.09	7.12	19.99	0.16
OF	72.40	67.24	76.31	0.91	0.95

• I₀ is the initial infiltration capacity of the soil; I_b is the infiltration capacity of the soil when saturated; h = e^(-k), in which k is an empirical parameter related to the soil type; K_s is the average time for emptying the surface reservoir; K_sub is the average time for emptying the underground reservoir; R_máx is the maximum rainfall that can be retained by the interception reservoir (vegetation cover and soil depressions); alfa is a parameter of the model, related to a coefficient that represents the percentage of rainfall that flows on the surface; and OF is the objective function used for model calibration.

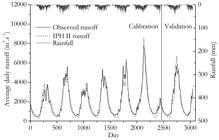
Hyetographs and hydrograms of the runoff observed and predicted by the model for the control units Porto Roncador, Teles Pires, Cachoeirão, Fazenda Tratex and Jusante Foz Peixoto de Azevedo can be visualized in Figures 4 , 5 , 6 , 7 and 8 , respectively

Figure 4
Runoff observed and estimated by the IPH II model for the Porto Roncador monitoring unit.

Figure 5
Runoff observed and estimated by the IPH II model for the Teles Pires monitoring unit.

Figure 6
Runoff observed and estimated by the IPH II model for the Cachoeirão monitoring unit.

Figure 7
Runoff observed and estimated by the IPH II model for the Fazenda Tratex monitoring unit.

Figure 8
Runoff observed and estimated by the IPH II model for the Jusante Foz Peixoto de Azevedo monitoring unit.

In general, a good agreement between the values of runoff observed and predicted by the IPH II model for the five monitoring units of the Teles Pires River basin is verified through a visual analysis. Despite this, it is evident in hydrograms ( Figures 4 to 8 ) a certain difficulty of the hydrological model to simulate some runoff floods and recessions.

Authors such as Moreira, Mine and Pereira Filho (2007), Pereira et al. (2014) , Pereira et al. (2016a , b ), Von Stackelberg, Chescheir and Skaggs (2007) and Viola et al. (2009) also found the same difficulty to predict peak runoff with rainfall-runoff models. The justification exposed by these authors is, among others, the difficulty of representing the spatial and temporal distribution of rainfall. Mello et al. (2008) also affirm that one of the possible explanations for less accuracy in the prediction of peak runoff is, in addition to the justifications already presented, the set of settings and input data provided to the hydrological model that makes it difficult to define representative values for the entire drainage area.

The quantitative measures of the IPH-II model performance are listed in Table 7 .

Table 7
Quantitative measures of the performance of the IPH II model in the calibration and validation steps for each monitoring unit.

Station	Step	MAE(1)	RMSE(2)	Bias	ENS(3)	d(4)	t(5)
1	calibration	72.40	135.40	-4.23	0.80	0.94	1.64(ns)
	validation	68.80	114.00	-2.25	0.77	0.94	0.55(ns)
2	calibration	67.24	111.17	1.91	0.82	0.94	0.78(ns)
	validation	77.21	128.08	2.71	0.86	0.96	0.78(ns)
3	calibration	76.31	111.91	-4.87	0.92	0.98	1.60(ns)
	validation	143.45	216.78	-2.14	0.84	0.95	0.36(ns)
4	calibration	97.57	141.32	-5.45	0.91	0.98	1.76(ns)
	validation	94.39	154.56	5.00	0.92	0.98	0.80(ns)
5	calibration	272.72	363.70	-5.35	0.95	0.99	0.73(ns)
	validation	282.07	390.82	11.30	0.93	0.98	0.72(ns)

• ⁽¹⁾MAE = mean absolute error;
• ⁽²⁾RMSE = root mean square error;
• ⁽³⁾Nash-Sutcliffe efficiency index;
• ⁽⁴⁾Willmott’s concordance index;
• ⁽⁵⁾paired t-test; ^(ns)non-significant. The terms d, E _NS and t are dimensionless, the remainder is in m³/s.

When analyzing the Nash-Sutcliffe efficiency index (E_NS), it is noted that the IPH II model was “adequate and good”, according to the classification of Van Liew et al. (2007) , to predict the runoff in the monitoring units of the Teles Pires River basin.

The values of the Willmott index confirmed that there was a good agreement between the runoff observed and predicted by IPH II in all five control units of the Teles Pires River analyzed in this study.

The bias indicated that the IPH-II model overestimated the runoff values in the control units Porto Roncador; Cachoeirão; Fazenda Tratex and Jusante Foz Peixoto de Azevedo; in the last two only in the calibration step. In the Teles Pires monitoring unit, there was underestimation in the calibration and validation steps.

Regarding the paired t-test at 5% significance, no significant t values were obtained in any of the monitoring units. Therefore, it is stated with 95% probability that the difference between the values predicted by the model and those observed is statistically null, an expected condition.

It can be seen in Table 7 that the distances between MAE and RMSE were not excessive indicating that the variance of the individual errors in the sample is acceptable.

Another point that draws attention in Table 7 is the performance of the model in the calibration and validation steps. The IPH II had adequate performance in the two steps, showing a reliable estimation of the runoff rates, although it presented a greater error in the validation in relation to the calibration.

The reduction in the performance of the rainfall-runoff hydrological model in the validation step was also reported by other authors, such as Fukunaga et al. (2015) , Monteiro et al. (2015) and Melo Neto et al. (2014) .

It should be emphasized that no hydrological model can provide a perfect result when applied at the river basin level, since science has not yet reached a complete knowledge about the physical processes of the hydrological cycle ( MAGALHÃES, 1989 ). For example, the results obtained with the IPH II model for the Teles Pires River basin, which despite errors, are at an acceptable level and did not compromise the reliability of the estimates.

The causes of the errors in the estimation of runoff of the Teles Pires River basin may be related to a set of factors, including: errors in the collection of hydrometeorological data, transformation of punctual data into spatial means and errors in the structure of the model due to simplifications of physical processes of the hydrological cycle.

When analyzing Table 7 , it is observed that the IPH-II model presented better performance to estimate the runoff rates in the sections with larger drainage area. According to Benaman, Shoemaker and Haith (2005) , Beskow et al. (2011) and Viola et al. (2009) , when rainfall-runoff models are performed on a daily time scale, especially in small and medium tropical watersheds, it is more difficult to obtain results with good accuracy due to the high spatial and temporal variability of rainfall as well as rapid displacement of the surface runoff.

SAC-SMA model

The parameters of the Sacramento (SAC-SMA) model calibrated automatically with the SCE-UA algorithm and the objective function for each monitoring unit of the Teles Pires River are in Table 8 .

Table 8
Value of the objective function (OF) and parameters of the SAC-SMA model obtained in the automatic calibration step with the SCE-UA algorithm.

Parameter	Unit	Station
		1	2	3	4	5
UZTWM	mm	93.89	1.018	48.17	144.33	4.30
UZFWM	mm	76.46	145.69	75.31	109.17	107.84
UZK	day-1	0.47	0.12	0.32	0.35	0.46
PCTIM	km2/km2	0.10	0.078	0.17	0.08	0.00
ADIMP	km2/km2	0.25	0.33	0.00	0.10	0.00
ZPERC	dimensionless	157.75	159.34	120.45	147.87	158.05
REXP	dimensionless	2.88	2.22	3.02	1.48	1.43
LZTWM	mm	137.36	300.59	144.18	143.69	197.77
LZFSM	mm	423.98	411.94	586.07	1.00	410.76
LZFPM	mm	755.60	1000	119.42	999.96	526.28
LZSK	day-1	0.23	0.15	0.00	0.25	0.01
LZPK	day-1	0.14	0.00	0.16	0.00	0.03
PFREE	mm mm-1	0.58	0.22	0.60	0.31	0.58
OF	dimensionless	0.87	0.91	0.94	0.94	0.93

• UZTWM = upper zone tension water maximum capacity (mm); UZFWM = upper zone free water maximum capacity (mm); LZTWM = lower zone tension water maximum capacity (mm); LZFPM = lower zone primary free water maximum capacity (mm); LZFSM = lower zone supplemental free water maximum capacity (mm); UZK = upper zone free water lateral depletion rate (day^-1); LZPK = lower zone primary free water depletion rate(day ^-1); LZSK = lower zone supplementary free water depletion rate (day^-1 ); PCTIM = fraction of the impervious area (km²/km² ); ADIMP = fraction of the additional impervious area (km²/km² ); PFREE = direct percolation fraction from upper to lower zone free water storage (mm/mm); ZPERC = maximum percolation rate coefficient (none); REXP = exponent of the percolation equation (none); and OF is the objective function used for model calibration.

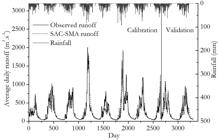
Hyetographs and hydrograms of the runoff observed and predicted by the model for the control units Porto Roncador, Teles Pires, Cachoeirão, Fazenda Tratex and Jusante Foz Peixoto de Azevedo are illustrated in Figures 9 , 10 , 11 , 12 and 13 , respectively. It can be observed in the hydrograms that the model presented difficulties to simulate extreme runoff rates, similar to IPH II.

Figure 9
Runoff observed and estimated by the Sacramento model for the Porto Roncador monitoring unit.

Figure 10
Runoff observed and estimated by the Sacramento model for the Teles Pires monitoring unit.

Figure 11
Runoff observed and estimated by the Sacramento model for the Cachoeirão monitoring unit.

Figure 12
Runoff observed and estimated by the Sacramento model for the Fazenda Tratex monitoring unit.

Figure 13
Runoff observed and estimated by the Sacramento model for the Jusante Foz Peixoto de Azevedo monitoring unit.

It is observed in the Fazenda Tratex control unit ( Figure 12 ) that the SAC-SMA model did not respond adequately to a rainfall event in the calibration step, excessively overestimating the runoff. In turn, in the validation for another rainfall event, it underestimated the runoff of the watercourse.

Table 9 lists the quantitative measures of the SAC-SMA (Sacramento) model performance.

Table 9
Quantitative measures of the performance of the SAC-SMA model in the calibration and validation steps for each monitoring unit.

Station	Step	MAE(1)	RMSE(2)	Bias	ENS(3)	d(4)	t(5)
1	calibration	70.29	128.81	2.82	0.83	0.95	1.13(ns)
	validation	64.53	100.42	-2.57	0.83	0.95	0.66(ns)
2	calibration	55.95	87.85	-1.92	0.89	0.97	0.94(ns)
	validation	83.29	142.51	-3.28	0.83	0.95	0.78(ns)
3	calibration	74.39	104.67	-2.44	0.93	0.98	0.82(ns)
	validation	129.09	196.89	-3.28	0.87	0.97	0.59(ns)
4	calibration	94.94	145.13	-11.91	0.90	0.98	3.65 *
	validation	133.53	199.17	104.13	0.89	0.97	13.85*
5	calibration	305.64	435.48	-3.97	0.92	0.98	0.44(ns)
	validation	276.08	399.68	17.83	0.94	0.98	1.01(ns)

• ⁽¹⁾MAE = mean absolute error;
• ⁽²⁾RMSE = root mean square error;
• ⁽³⁾Nash-Sutcliffe efficiency index;
• ⁽⁴⁾Willmott’s concordance index;
• ⁽⁵⁾paired t-test; ^(ns)non-significant;
• ^*
  Significant at 5% significance. The terms d, E_NS and t are dimensionless, the remainder is in m³/s.

Based on the Nash-Sutcliffe coefficient (E_NS), it is stated that the performance of the SAC-SMA model was classified as “adequate and good” in the four adjusted monitoring units.

The value of the Willmott concordance index indicates that there was good agreement between the data simulated by the Sacramento model and those observed in the five adjusted basis, which is close to 1.

It is noted in Table 9 that the distances between MAE and RMSE values were not excessive indicating that the variance of the individual errors in the sample is acceptable.

The bias indicated that the SAC-SMA model, in general, overestimated the runoff in the Teles Pires River basin. It is highlighted the high bias values of the Fazenda Tratex monitoring unit (Station 4) due to the errors of runoff estimation mentioned above.

Regarding the paired t-test at 5% significance, the SAC-SMA model obtained significant values of t only for station 4 (Fazenda Tratex) indicating the existence of a significant difference between the runoff observed and simulated by the model. In this case, the SAC-SMA should not be used to estimate the runoff rates although the other indices indicate acceptable performance. When analyzing Table 9 , it is observed that the SAC-SMA model presented better performance to estimate the runoff rates of the sections with larger area, similar to the IPH-II model. Exception to this was the result obtained for station 4 (Fazenda Tratex).

For the monitoring units 1 (Porto Roncador), 2 (Teles Pires), 3 (Cachoeirão) and 5 (Jusante Foz Peixoto de Azevedo) the SAC-SMA had adequate performance in the two steps (calibration and validation), proving to be reliable to estimate the average daily flows.

Maximum, minimum and average runoff rates and comparison between models

Comparing the quantitative measures of the performance of the IPH-II and SAC-SMA models ( Tables 7 and 9 ), it was observed that the IPH-II model presented better results for runoff estimation in the monitoring units 2 (Teles Pires), 4 (Fazenda Tratex) and 5 (Jusante Foz Peixoto de Azevedo) in the Teles Pires River basin.

The SAC-SMA model presented better results for runoff estimation in units 1 (Porto Roncador) and 3 (Cachoeirão). Despite this result for the SAC-SMA, it is highlighted that the IPH-II model obtained adjustment for all five basins of the study, unlike the Sacramento model.

It was possible to verify that the IPH II model is less complex in comparison to the SAC-SMA, of easy computational manipulation and has a smaller number of parameters, which represent a great advantage in the Brazilian conditions.

The application of IPH II and SAC-SMA in the Teles Pires River basin also made clear that the complexity of a rainfall-runoff hydrological model is not necessarily synonymous with better estimates. Although the SAC-SMA model was more complex and presented a greater detail of the hydrological processes, it was not able to outperform the IPH II model in all runoff monitoring units analyzed.

Table 10 presents the mean values of the maximum, minimum and average runoff observed and estimated with the IPH II and SAC-SMA models.

Table 10
Mean of the maximum, minimum and average runoff values estimated and predicted by IPH II and SAC-SMA models.

Model			IPH II			SAC-SMA
Runoff			Qmáx.	Qméd.	Qmín.	Qmáx.	Qméd.	Qmín.
Station	1	E	1123	260	47	1081	259	39
		O	1283	266	45	1324	264	45
	2	E	1133	340	84	1103	343	88
		O	1245	343	90	1245	343	90
	3	E	2053	835	338	1882	861	320
		O	2083	854	362	2083	854	362
	4	E	1957	864	384	2064	880	413
		O	1937	863	394	1937	865	394
	5	E	5622	2144	384	5613	2113	379
		O	5502	2138	583	5502	2138	583

• E = estimated runoff; O = observed runoff; Q_máx. = mean of the annual maximum daily runoff (m³ s^-1); Q_méd . = mean of the annual average daily runoff (m³ s^-1); Q _mín. = mean of the annual minimum daily runoff (m³ s ^-1).

It can be seen in Table 10 that the IPH II model presented better results for maximum runoff estimation in units 1 to 4. In these sections, the model underestimated the maximum runoff in sections 1, 2 and 3 by 12.5, 9.0 and 1.4%, respectively. In the monitoring unit 4, the IPH II model overestimated the maximum runoff rate by approximately 1%.

It is observed in Table 10 that for unit 5, the SAC-SMA model presented a smaller error, compared to IPH II, for maximum runoff estimation. The Sacramento model overestimated the maximum runoff rate in this section by approximately 2%.

As for the mean runoff rate, Table 10 shows that both IPH II and SAC-SMA adequately estimated it with underestimates and overestimations of approximately 2%. The SAC-SMA model estimated the mean runoff with minor error in units 1, 2 and 3, while the IPH II in units 4 and 5.

When analyzing the minimum runoff observed and estimated in Table 10 , it can be seen that the IPH II model better estimated these values in units 1, 3 and 4. The model overestimated the minimum runoff in section 1 by 4.4% and underestimated by 6.6 and 2.5% in units 3 and 4, respectively. In the monitoring unit 5 both the IPH II and the SAC-SMA models significantly underestimated the minimum runoff (65%). This underestimation is evident in the hydrograms of Figures 8 and 13 .

With the exception of unit 5 for the minimum runoff, it was verified with the analysis of Table 10 that the IPH II and SAC-SMA models adequately estimated the maximum, minimum and average runoff rates.

CONCLUSIONS

Based on the results obtained, it can be stated that:

• The IPH-II and SAC-SMA conceptual models are suitable for daily runoff modeling in the Tele Pires River basin and can be used for the elaboration of scenarios for planning and management of water resources in the basin, runoff forecast on the basis of rainfall as well as for analysis of consistency and filling of missing runoff data;

• The hydrological models IPH II and SAC-SMA present better performance for runoff estimation in river basins with larger drainage area;

• The complexity of a rainfall-runoff hydrological model is not necessarily synonymous with better estimates. Although the SAC-SMA model is more complex and presents greater detail of the hydrological processes, it has not been able to outperform the IPH II model in all runoff monitoring units of the Teles Pires River.

ACKNOWLEDGEMENTS

The authors are grateful to the Foundation for Research Support of the State of Mato Grosso (FAPEMAT) for financial support for the research project (process Nº. 189567/2015).

REFERENCES

• ANA – AGÊNCIA NACIONAL DE ÁGUAS. Levantamento da agricultura Irrigada por Pivôs Centrais no Brasil: relatório síntese. Brasília: ANA, 2016.
• ANDRADE, M. A.; MELLO, C. R.; BESKOW, S. Simulação hidrológica em uma bacia hidrográfica representativa dos latossolos na região Alto Rio Grande, MG. Revista Engenharia Agrícola e Ambiental, v. 17, n. 1, p. 69-76, 2013. http://dx.doi.org/10.1590/S1415-43662013000100010.
  » http://dx.doi.org/10.1590/S1415-43662013000100010
• ANDREWS, F. T.; CROKE, B. F. W.; JAKEMAN, A. J. An open software environment for hydrological model assessment and development. Environmental Modelling & Software , v. 26, n. 10, p. 1171-1185, 2011. http://dx.doi.org/10.1016/j.envsoft.2011.04.006.
  » http://dx.doi.org/10.1016/j.envsoft.2011.04.006
• ARABI, M.; GOVINDARAJU, R. S.; HANTUSH, M. M. A probabilistic approach for analysis of uncertainty in the evaluation of watershed management practices. Journal of Hydrology , v. 333, n. 1, p. 459-471, 2006.
• BENAMAN, J.; SHOEMAKER, C. A.; HAITH, D. A. Calibration and validation of soil and water assessment tool on an agricultural watershed in upstate New York. Journal of Hydrologic Engineering , v. 10, n. 5, p. 363-374, 2005. http://dx.doi.org/10.1061/(ASCE)1084-0699(2005)10:5(363).
  » http://dx.doi.org/10.1061/(ASCE)1084-0699(2005)10:5(363)
• BERTONI, J. C.; TUCCI, C. E. M.; CLARKE, R. T. Rainfall-based real-time flood forecasting. Journal of Hydrology, v. 131, n. 1, p. 313-339, 1992. http://dx.doi.org/10.1016/0022-1694(92)90224-J.
  » http://dx.doi.org/10.1016/0022-1694(92)90224-J
• BESKOW, S.; MELLO, C. R.; NORTON, L. D.; SILVA, A. M. Performance of a distributed semi-conceptual hydrological model under tropical watershed conditions. Catena, v. 86, n. 3, p. 160-171, 2011. http://dx.doi.org/10.1016/j.catena.2011.03.010.
  » http://dx.doi.org/10.1016/j.catena.2011.03.010
• BOUGHTON, W. Catchment water balance modelling in Australia 1960-2004. Agricultural Water Management, v. 71, n. 2, p. 91-116, 2005. http://dx.doi.org/10.1016/j.agwat.2004.10.012.
  » http://dx.doi.org/10.1016/j.agwat.2004.10.012
• BRAVO, M. J.; ALLASIA, D. G.; COLLISCHONN, W.; TASSI, R.; MELLER, A.; TUCCI, C. E. M. WIN_IPH2: modelo IPHII para Windows®: manual de conceitos versão 1.0. Porto Alegre: UFRGS/IPH, 2006.
• BREDA, A.; GONÇALVES, J. E.; SILVEIRA, R. B. Análise de alterações em componentes de um método de calibração automática mono-objetivo na qualidade e eficiência do ajuste de parâmetros do Modelo Sacramento. Revista Brasileira de Recursos Hídricos, v. 16, n. 2, p. 89-100, 2011. http://dx.doi.org/10.21168/rbrh.v16n2.p89-100.
  » http://dx.doi.org/10.21168/rbrh.v16n2.p89-100
• BRUN, G. W.; TUCCI, C. E. M. Previsão em tempo real do volume afluente ao reservatório de Ernestina. Revista Brasileira de Recursos Hídricos, v. 6, n. 2, p. 73-79, 2001. http://dx.doi.org/10.21168/rbrh.v6n2.p73-79.
  » http://dx.doi.org/10.21168/rbrh.v6n2.p73-79
• BURNASH, R. J. C. The NWS riverforecast system: catchmentmodeling. In: SINGH, V. P. (Ed.). Computer models of watershed hydrology Highlands Ranch: Water Resources Publications, 1995.
• BURNASH, R. J. C.; FERRAL, L. Conceptualization of the sacramento soil moisture accounting model Silver Spring: US Dept of Commerce, 1996. Available from: <http://www.nws.noaa.gov/oh/hrl/nwsrfs/ users_manual/part2/_pdf/23sacsma.pdf>. Access on: 1 sept. 2007.
  » http://www.nws.noaa.gov/oh/hrl/nwsrfs/
• DEVIA, G. K.; GANASRI, B. P.; DWARAKISH, G. S. A review on hydrological models. Aquatic Procedia, v. 4, n. 1, p. 1001-1007, 2015. http://dx.doi.org/10.1016/j.aqpro.2015.02.126.
  » http://dx.doi.org/10.1016/j.aqpro.2015.02.126
• DUAN, Q.; SOROOSHIAN, S.; GUPTA, V. K. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resources Research, v. 28, n. 4, p. 1015-1031, 1992. http://dx.doi.org/10.1029/91WR02985.
  » http://dx.doi.org/10.1029/91WR02985
• EPE – EMPRESA DE PESQUISA ENERGÉTICA. Avaliação ambiental integrada da bacia hidrográfica do rio Teles Pires: relatório final: sumário executivo. Rio de Janeiro: EPE , 2009. Available from: <http://www.epe.gov.br/MeioAmbiente/Documents/AAI%20Teles%20Pires/AAI%20Teles%20Pires%20-%20Relat%C3%B3rio%20Final%20%20Sum%C3%A1rio%20Executivo.pdf>. Access on: 5 dec. 2016.
  » http://www.epe.gov.br/MeioAmbiente/Documents/AAI%20Teles%20Pires/AAI%20Teles%20Pires%20-%20Relat%C3%B3rio%20Final%20%20Sum%C3%A1rio%20Executivo.pdf
• FUKUNAGA, D. C.; CECILIO, R. A.; ZANETTI, S. S.; OLIVEIRA, L. T.; CAIADO, M. A. C. Application of the SWAT hydrologic model to a tropical watershed at Brazil. Catena , v. 125, n. 1, p. 206-213, 2015. http://dx.doi.org/10.1016/j.catena.2014.10.032.
  » http://dx.doi.org/10.1016/j.catena.2014.10.032
• GOMES, L. F. C.; MONTENEGRO, S. M. G. L.; VALENÇA, M. J. S. Modelo baseado na técnica de redes neurais para previsão de vazões na bacia do rio São Francisco. Revista Brasileira de Recursos Hídricos, v. 15, n. 1, p. 5-15, 2010. http://dx.doi.org/10.21168/rbrh.v15n1.p5-15.
  » http://dx.doi.org/10.21168/rbrh.v15n1.p5-15
• HUANG, G.; KADIR, T.; CHUNG, F. Hydrological response to climate warming: the upper feather river watershed. Journal of Hydrology, v. 426-427, p. 138-150, 2012. http://dx.doi.org/10.1016/j.jhydrol.2012.01.034.
  » http://dx.doi.org/10.1016/j.jhydrol.2012.01.034
• KLEMES, V. Operational testing of hydrological simulation models. Hydrological Sciences Journal, v. 31, n. 1, p. 13-24, 1986. http://dx.doi.org/10.1080/02626668609491024.
  » http://dx.doi.org/10.1080/02626668609491024
• KOUTROULIS, A. G.; TSANIS, I. K.; DALIAKOPOULOS, I. N.; JACOB, D. Impact of climate change on water resources status: a case study for Crete Island, Greece. Journal of Hydrology , v. 479, p. 146-158, 2013. http://dx.doi.org/10.1016/j.jhydrol.2012.11.055.
  » http://dx.doi.org/10.1016/j.jhydrol.2012.11.055
• MACÊDO, M. N. C.; DIAS, H. C. T.; COELHO, F. M. G.; ARAÚJO, E. A.; SOUZA, M. L. H.; SILVA, E. Precipitação pluviométrica e vazão da bacia hidrográfica do Riozinho do Rôla, Amazônia Ocidental. Ambiente & Água., v. 8, n. 1, p. 206-221, 2013.
• MAGALHÃES, P. C. Hidrologia superficial. In: RAMOS, F.; OCCHIPINTI, A. G.; VILLA NOVA, N. A.; REICHARDT, K.; MAGALHÃES, P. C.; CLEARY, R. W. Engenharia hidrológica . Rio de Janeiro: ABRH, 1989. p. 199-289.
• MELLO, C. R.; NORTON, L. D.; PINTO, L. C.; BESKOW, S.; CURI, N. Agricultural watershed modeling: a review for hydrology and soil erosion processes. Ciência e Agrotecnologia , v. 40, n. 1, p. 7-25, 2016. http://dx.doi.org/10.1590/S1413-70542016000100001.
  » http://dx.doi.org/10.1590/S1413-70542016000100001
• MELLO, C. R.; VIOLA, M. R.; NORTON, L. D.; SILVA, A. M.; WEIMAR, F. A. Development and application of a simple hydrologic model simulation for a brazilian headwater basin. Catena , v. 75, n. 3, p. 235-247, 2008. http://dx.doi.org/10.1016/j.catena.2008.07.002.
  » http://dx.doi.org/10.1016/j.catena.2008.07.002
• MELO NETO, J. O.; SILVA, A. M.; MELLO, C. R.; MELLO JÚNIOR, A. V. Simulação Hidrológica Escalar com o Modelo SWAT. Revista Brasileira de Recursos Hídricos , v. 19, n. 1, p. 177-188, 2014. http://dx.doi.org/10.21168/rbrh.v19n1.p177-188.
  » http://dx.doi.org/10.21168/rbrh.v19n1.p177-188
• MINE, M. R. M.; TUCCI, C. E. M. Previsão em tempo real de vazões afluentes a reservatórios de usinas hidrelétricas. Revista Brasileira de Recursos Hídricos , v. 4, n. 2, p. 73-95, 1999. http://dx.doi.org/10.21168/rbrh.v4n2.p73-95.
  » http://dx.doi.org/10.21168/rbrh.v4n2.p73-95
• MONTEIRO, J. A.; STRAUCH, M.; SRINIVASAN, R.; ABBASPOUR, K.; GUCKER, B. Accuracy of grid precipitation data for Brazil: application in river discharge modelling of the Tocantins catchment. Hydrological Processes, v. 30, n. 9, p. 1419-1430, 2015. http://dx.doi.org/10.1002/hyp.10708.
  » http://dx.doi.org/10.1002/hyp.10708
• MOREIRA, I. A.; MINE, M. R. M.; PEREIRA FILHO, A. J. Modelagem hidrológica chuva-vazão com dados de radar e pluviômetros. Ingeniería del Agua , v. 14, n. 2, p. 83-96, 2007. http://dx.doi.org/10.4995/ia.2007.2904.
  » http://dx.doi.org/10.4995/ia.2007.2904
• NÓBREGA, M. T.; COLLISCHONN, W.; TUCCI, C. E. M.; PAZ, A. R. Uncertainty in climate change impacts on water resources in the Rio Grande Basin, Brazil. Hydrology and Earth System Sciences, v. 15, n. 2, p. 585-595, 2011. http://dx.doi.org/10.5194/hess-15-585-2011.
  » http://dx.doi.org/10.5194/hess-15-585-2011
• OLIVEIRA, V. G.; LIMA, C. H. R. Previsões multiescala de vazões para o sistema hidrelétrico brasileiro utilizando ponderação bayesiana de modelos (BMA). Revista Brasileira de Recursos Hídricos, v. 21, n. 3, p. 618-635, 2016. http://dx.doi.org/10.1590/2318-0331.011616032.
  » http://dx.doi.org/10.1590/2318-0331.011616032
• PECHLIVANIDIS, I. G.; JACKSON, B. M.; MCINTYRE, N. R.; WHEATER, H. S. Catchment Scale Hydrological Modelling: a review of model types, calibration approaches and uncertainty analysis methods in the context of recent developments in technology and applications. Global NEST Journal, v. 13, n. 3, p. 193-214, 2011.
• PEREIRA, D. R.; MARTINEZ, M. A.; ALMEIDA, A. Q.; PRUSKI, F. F.; SILVA, D. D.; ZONTA, J. H. Hydrological simulation using SWAT model in headwater basin in southeast Brazil. Engenharia Agrícola, v. 34, n. 4, p. 789-799, 2014. http://dx.doi.org/10.1590/S0100-69162014000400018.
  » http://dx.doi.org/10.1590/S0100-69162014000400018
• PEREIRA, D. R.; MARTINEZ, M. A.; SILVA, D. D.; PRUSKI, F. F. Hydrological simulation in a basin of typical tropical climate and soil using the SWAT model part I: calibration and validation tests. Journal of Hydrology: Regional Studies, v. 7, n. 1, p. 14-37, 2016a.
• PEREIRA, D. R.; ULIANA, E. M.; MARTINEZ, M. A.; SILVA, D. D. Desempenho de um modelo hidrológico concentrado e de um semidistribuído na predição de vazões diárias. Irriga, v. 21, n. 2, p. 409-424, 2016b. http://dx.doi.org/10.15809/irriga.2016v21n2p398-413.
  » http://dx.doi.org/10.15809/irriga.2016v21n2p398-413
• SHIN, M.; GUILLAUME, J. H. A.; CROKE, B. F. W.; JAKEMAN, A. J. Addressing ten questions about conceptual rainfall–runoff models with global sensitivity analyses in R. Journal of Hydrology, v. 503, p. 135-152, 2013. http://dx.doi.org/10.1016/j.jhydrol.2013.08.047.
  » http://dx.doi.org/10.1016/j.jhydrol.2013.08.047
• TANAKA, A. A.; SOUZA, A. P.; KLAR, A. E.; SILVA, A. C.; GOMES, A. W. A. Evapotranspiração de referência estimada por modelos simplificados para o Estado do Mato Grosso. Pesquisa Agropecuária Brasileira, v. 51, n. 2, p. 91-104, 2016. http://dx.doi.org/10.1590/S0100-204X2016000200001.
  » http://dx.doi.org/10.1590/S0100-204X2016000200001
• TUCCI, C. E. M. Modelos hidrológicos Porto Alegre: Editora UFRGS, 2005.
• TUCCI, C. E. M.; CLARKE, R. T.; COLLISCHONN, W. Previsão de vazões com base na previsão climática Brasília: ANEEL, 2003.
• ULIANA, E. M. Modelagem da vazão em cursos de água com base em modelos conceituais chuva-vazão e em método de inteligência artificial . 2016. 143 f. Tese (Doutorado em Engenharia Agrícola) - Departamento de Engenharia Agrícola, Universidade Federal de Viçosa, Viçosa, 2016. Available from: <http://www.locus.ufv.br/ handle/123456789/10997>. Access on: 10 oct. 2018.
  » http://www.locus.ufv.br/
• VAN LIEW, M. W.; VEITH, T. L.; BOSCH, D. D.; ARNOLD, J. G. Suitability of SWAT for the Conservation effects assessment project: A comparison on USDA-ARS watersheds. Journal of Hydrologic Engineering, v. 12, n. 2, p. 173-189, 2007. http://dx.doi.org/10.1061/(ASCE)1084-0699(2007)12:2(173).
  » http://dx.doi.org/10.1061/(ASCE)1084-0699(2007)12:2(173)
• VAN WERKHOVEN, K.; WAGENER, T.; REED, P.; TANG, Y. Sensitivity guided reduction of parametric dimensionality for multi-objective calibration of watershed models. Advances in Water Resources, v. 32, n. 8, p. 1154-1169, 2009. http://dx.doi.org/10.1016/j.advwatres.2009.03.002.
  » http://dx.doi.org/10.1016/j.advwatres.2009.03.002
• VAZE, J.; POST, D. A.; CHIEW, F. H. S.; PERRAUD, J. M.; VINEY, N. R.; TENG, J. Climate non-stationarity: validity of calibrated rainfall-runoff models for use in climate change studies. Journal of Hydrology, v. 394, n. 3-4, p. 447-457, 2010. http://dx.doi.org/10.1016/j.jhydrol.2010.09.018.
  » http://dx.doi.org/10.1016/j.jhydrol.2010.09.018
• VIOLA, M. R.; MELLO, C. R.; ACERBI JUNIOR, F. W.; SILVA, A. M. Modelagem hidrológica na bacia hidrográfica do rio Aiuruoca, MG. Revista Brasileira de Engenharia Agrícola e Ambiental, v. 13, n. 5, p. 581-590, 2009. http://dx.doi.org/10.1590/S1415-43662009000500011.
  » http://dx.doi.org/10.1590/S1415-43662009000500011
• VON STACKELBERG, N. O.; CHESCHEIR, G. M.; SKAGGS, R. W. Simulation of the hydrologic effects of afforestation in the Tacuarembo River Basin, Uruguay. Transactions of the ASABE , v. 50, n. 2, p. 455-468, 2007. http://dx.doi.org/10.13031/2013.22636.
  » http://dx.doi.org/10.13031/2013.22636
• WENZEL, D. A.; ULIANA, E. M.; ALMEIDA, F. T.; SOUZA, A. P.; MENDES, M. A. S. A.; SOUZA, L. G. Características fisiográficas de sub-bacias do Médio e Alto Rio Teles Pires, Mato Grosso. Revista de Ciências Agroambientais, v. 15, n. 2, p. 1-9, 2017.

Publication Dates

• Publication in this collection
  11 Apr 2019
• Date of issue
  2019

History

• Received
  26 May 2018
• Reviewed
  10 Oct 2018
• Accepted
  03 Feb 2019