EFFECT OF NON-DARCY FLOW COEFFICIENT VARIATION DUE TO WATER VAPORIZATION ON WELL PRODUCTIVITY OF GAS CONDENSATE RESERVOIRS

Abstract

Well productivity of gas condensate reservoirs is highly affected by near-wellbore phenomena. Inertial force resulting from convective acceleration of fluid particles in the medium, as well as viscous force, determines the flow of gas through porous media at high velocity. Pressure drop builds up the molar content of water in gas by water vaporization in the near-wellbore region, which means a drop in connate water saturation. Given that the inertial force is a function of the non-Darcy coefficient, β, which itself depends upon connate water saturation, this can ultimately lessen the non-Darcy component of the pressure drop and therefore inertial forces, leading to improvement of well deliverability. Currently, no physically relevant model takes into account the non-Darcian flow coefficient variation due to this phenomenon. This paper utilizes a single-well compositional simulation to exhibit how water vaporization could compensate for the effect of inertia on well productivity of gas condensate reservoirs.

Gas condensate reservoirs; Well productivity; Non-Darcy flow; Water vaporization; Simulation

INTRODUCTION

Gas condensate reservoirs are becoming more common as deeper depths are being targeted in the exploration for oil and gas. The behaviors of such systems are complex and are still not fully understood, especially in the near-wellbore region. (Gringarten et al., 2006).

When the flowing bottomhole pressure in gas condensate wells drops below the dew point, a condensate bank is created within the near wellbore region. This reduces the gas relative permeability around the well and leads to a loss of well productivity. Furthermore, accumulation of the condensate liquid within the near wellbore region leads to reduction of the effective flow area and consequently will increase the gas velocity at the wellbore. Therefore the non-Darcy flow coefficient and its related skin factor will increase. In the reservoir, far from the wellbore, flow rates are low and Darcy's law remains valid, but near the wellbore, high-pressure gradients induce both large condensate saturation and high gas velocities, which may lead to significant deviations from Darcy's law for the gas permeability (Lombard. et al., 2000).

Deviations from Darcy's law (Non-Darcy or inertial flow effects) will reduce the well productivity. The magnitude of this effect depends on the value of the Non-Darcy flow coefficient β.

Investigations have shown that the dependency of the inertial coefficient β on the rock properties, especially the water saturation (Coles and Hartman, 1998; Kalaydijan et al., 1996; Geerstma, 1974). A reduction in water saturation can reduce the inertial coefficient.

In gas condensate reservoirs, gas is initially in equilibrium with water at reservoir conditions. However, once a well is placed in production, the pressure drop that occurs around the well bore causes an increase in the molar content of water in the gas phase (Grattoni et al., 2009; Zuluaga and Lake, 2008, 2005; Morin and Montel, 1995; Kamath and Laroche, 2000).

Water vaporization that happens in high-temperature gas-condensate reservoirs shrinks the water saturation, which in turn elevates the gas saturation. Therefore, it is very important to consider the effect of water vaporization in gas condensate reservoirs.

In order to consider this effect, fine-grid compositional simulations or simulations using local grid refinement (LGR) near the wells can be used for accurate estimates of the well deliverability.

Water vaporization has been observed and reported in many HP/HT gas reservoirs. The first published report in this regard came from the Arun field in Indonesia (Bette and Heinemann, 1989). In this field, water was produced at the surface, while no water influx occurred. There have been some attempts to model water vaporization for flow through permeable media (Bette and Heinemann, 1989; Kurihara et al., 2000). Dodson and Standing (1994) reported experimental studies in PVT cells to determine the solubility of natural gas in brine and to determine the solubility of water in natural gas. It was found that the mole fraction of water in the gas phase increased with temperature and decreased with pressure.

Zuluaga and Monsalve (2003) experimentally examined the rate of water vaporization in core samples at initial water saturation. Other authors, namely Lee (1999) and Bette and Heinemann (1989), modified compositional simulators to account for mass transfer between water and hydrocarbon components to enable them to predict the amount of water vaporization.

Zuluaga and Lake (2005) devised a mathematical model for estimation of the water saturation profile owing to vaporization in dry gas reservoirs. Despite these efforts, there has not yet been any mathematical model for water vaporization in gas condensate reservoirs. In order to clarify the vaporization in a gas condensate reservoir, the authors developed a new semi-analytical model for these reservoirs and compared the results to those of the commercial compositional simulator GEM (see the appendix of this paper). It is important to know that our scope of work in this paper is the variation of the non-Darcy coefficient due to water vaporization.

In this paper, the commercial compositional simulator GEM was used to investigate the effect of water vaporization and its change on the non-Darcy flow coefficient and productivity index of the well.

THEORETICAL BACKGROUND

In the case of fluid flow through a porous medium far from the wellbore region, the pressure drop in the flow direction is proportional to the fluid velocity. The mathematical statement of this relationship is Darcy's law, which for radial flow is:

where μ is the fluid viscosity, k is the permeability and u is the fluid velocity, as defined by the following equation.

The region near the wellbore plays a key role in the productivity of gas condensate wells. In this region, due to higher gas flow rates in addition to viscous forces, the inertial force acts mainly as a result of convective acceleration of the fluid and also becomes significant. In the literature, many studies have been done to understand the invalidation of Darcy's law when the gas flow rate is high (Fancher and Lewis, 1933; Cornell and Katz, 1953; Tek et al., 1962). Forchheimer suggests the application of the equation below for calculating pressure drop at high flow rates:

In this equation, the first and second terms respectively represent the Darcy and non-Darcy components. In the latter, β is the coefficient of inertial

resistance for the gas. The non-Darcy component is negligible at low velocities and is generally omitted from the flow equation. In the case of gas flow, how-ever, since the viscosity is small, the non-Darcy component is always included, and Forchheimer's equation is applied instead of Darcy's. It is also noteworthy that the non-Darcy flow is conventionally used in flow equations as an additional skin factor.

Flow of a gas in porous media under non-Darcy conditions is described by Equation (4) (Dake, 1982).

where D is a function of β

The single-phase inertial resistance factor, β, is a fundamental rock property. It is sometimes referred to as the turbulence factor and can be calculated from the Geerstma correlation, as follows.

Noman and Archer (1987) summarized the original inertial effects, as well as the influence that fluid properties and pore structure would exert on β. They found that inertial effects for gases are stronger in the presence of mobile liquid compared to the immobile case. Lombard et al. (1999) developed Equation (6), based on experimental data, to calculate the inertia coefficient.

with kg in m², βg in m^-1.

As the pressure drop is increased and developed, the molar content of water in the gas phase increases exponentially and results in connate water vaporization, especially near the wellbore. This variation in connate water saturation (S_wi) could alter water-sensitive reservoir parameters such as the inertial resistance factor (β). Reduction of the connate water saturation causes a decrease in β, which can improve well productivity.

The compositional simulator GEM can predict the water saturation profile during production under such circumstances. This research presents a singlewell compositional simulation study to investigate the effects of water vaporization on the inertia resistance factor and well productivity of a high-pressure, high-temperature Iranian gas condensate reservoir.

SIMULATION MODEL SETUP

A compositional simulation was conducted to predict individual well performance. An example of a vertical well is presented in this paper. The effect of condensate banking, non-Darcy flow and water vaporization was captured through use of very fine grids near the well.

Synthetic Reservoir Model

The synthetic high-temperature gas condensate reservoir, at equilibrium with connate water, was described by 60×1×1 radial grids. Finer grids were chosen around the closely-spaced production wells to obtain better resolution. The smallest and innermost grid was 0.25 ft and the largest grid, the outermost one, 600 ft in radius. Relative permeability was constructed by the Corey equation (Corey, 1954). The three-parameter Peng- Robinson equation of state (Peng and Robinson, 1976), as utilized in the compositional simulator, was used to model the PVT behavior of reservoir fluids. The simulation modeling involved a number of considerations. First, the significance of water vaporization requires that water be a component in the fluid model. Second, the parameters of the equation of state must be tuned with experimental data. The simulation was run for 1800 days of production. Water vaporization is not incorporated in some compositional simulators, but GEM (compositional simulator of CMG) can simulate this effect. The radial well model properties are summarized in Table 1.

Table 1
Parameters for gas condensate reservoir simulation.

Parameter	Value
External radius	5000 ft
Wellbore radius	0.5 ft
Thickness	45ft
Permeability	30 md
Porosity	10%
Connate water saturation	20%
Temperature	217°F
volumetric flow rate	20 MMSCFD
Simulation grid cell	60×1×1
Relative permeability	Corey
Initial pressure	6000 psi
Dew point pressure	4815 psi

Reservoir Fluid Description

One of the Iranian gas condensate reservoir fluids was applied to the radial synthetic model. Standard PVT experiments were performed to determine the

dew point pressure, and liquid dropouts in constant composition expansion (CCE) and constant volume depletion (CVD) at the reservoir temperature (217 ºF). Winprop was used to make the fluid model and regression was based on observed data. PVT properties were predicted by the three-parameter Peng-Robinson equation of state and fluid viscosity by the JossiStiel-Thados correlation. Components were decreased to 7 pseudo-components by grouping (lumping). Some changes were made in critical properties and acentric factors and volume shifts were done to make the fluid model approximate observed data more closely.

Components and pseudo component compositions are shown in Table 2 and Table 3. The calculated dew-point at the reservoir temperature, 217 ºF, was close to 4815 psi. By grouping components into these 7 pseudo-components and changing critical properties, acentric factors and volume shifts, the fluid model was tuned very satisfactorily.

Table 2
Fluid composition before lumping.

Component	Mole %
N2	3.9
CO2	1.98
H2S	0.42
C1	82.49
C2	5.13
C3	1.86
i-C4	0.4
n-C4	0.67
i-C5	0.3
n-C5	0.28
C6	0.35
C7	0.45
C8	0.44
C9	0.29
C10	0.24
C11	0.17
C12	0.13
C13	0.12
C14	0.09
C15	0.07
C16	0.05
C17	0.04
C18	0.04
C19	0.03
C20	0.06

Table 3
Composition of pseudo components.

Pseudo components	Mole %
GP1=N2+C1+C2	91.52
GP2=CO2+H2S	2.4
GP3=C3+i-C4+n-C4	2.93
GP4=i-C5+n-C5-C6	0.93
GP5=C7-C10	1.42
GP6=C11-C18	0.71
GP7=C19-C20	0.09

Figure 1 and Figure 2 show calculated and laboratory observed data for different parameters in the CVD and CCE experiments. Figure 3 also shows the P-T diagram of the fluid sample.

Figure 1
Observed and calculated liquid saturation for the CVD experiment.

Figure 2
Observed and calculated relative volume for the CCE experiment.

Figure 3
P-T diagram of the fluid.

Inclusion of Non-Darcy Flow and Water Vaporization into Data Files

Three scenarios were designed to study water vaporization in this paper. The first one was the base case in which the effect of non-Darcy flow was not considered in the simulation. In the second case, the non-Darcy phenomenon was taken into account for the flow of gas at high velocity. This is imported by the *NONDARCY 1 keyword that utilizes the Geerstma correlation for calculation of the inertial coefficient. Finally, water vaporization was studied by inclusion of *H2O_INCLUDED or *OGW_FLASH *ON keywords to permit connate water vaporization during production.

RESULTS AND DISCUSSION

The compositional simulation was run. Figure 4 shows the connate water saturation versus distance at different times after production. It could be observed that the formation dried up to a distance of 7.5 ft after 800 days of production. If the pressure declines, the molar content of water in the gas phase will increase. As the vaporization front moves within the reservoir far from the well, the formation dries further to nearly 12 feet after 1000 days. Figure 5 also shows how connate water saturation gradually drops at different locations near the wellbore.

Figure 4
Connate water saturation distribution within the reservoir due to water vaporization at different times.

Figure 5
Variation of water saturation at different locations with respect to time.

As mentioned earlier, the inertial resistance factor (β) is inversely proportional to (1-S_wi). The relationship between β and S_wi is shown in Figure 6. Non-Darcy flow, which is a function of the inertial resistance factor (β), becomes more significant near the wellbore. On the other hand, water vaporization reduces the inertial resistance factor (Figure 7), which leads to hindrance of the effects of non-Darcy flow. According to Equation (4), non-Darcy flow creates an additional wellbore pressure drop, decreasing bottom-hole pressure with respect to the base case. On the contrary, water vaporization exerts an opposite effect compared to the non-Darcy case. Figure 8 illustrates the bottom-hole pressure in different scenarios. It is shown that water vaporization could compensate for the negative effect of inertia and elevate the bottom-hole pressure up to the base case value.

Figure 6
The relationship between inertial coefficient and water saturation.

Figure 7
Inertial coefficient at different locations during gas production.

Figure 8
Well bottom-hole pressure given for three different cases: neglecting non-Darcy flow, considering the inertial effect and finally considering water vaporization, respectively.

The productivity index (PI) describes the degree of communication between a well and the reservoir, and can be calculated from field measurements. The productivity index varies with the fluid mobility at the well and this is a well-accepted PI expression for gas wells, according to the following equation:

The productivity index is directly proportional to the bottom-hole pressure. Hence, any factor that could improve bottom-hole pressure will have a positive impact on the productivity index. As Figure 8 illustrates, water vaporization could increase the bottom-hole pressure with respect to the non-Darcy case. Therefore, it could change the productivity index of gas condensate wells. Figure 9 demonstrates the variation of the PI in three different scenarios. It is noticeable that water vaporization could compensate for the negative effect of non-Darcy flow.

Figure 9
Productivity index (PI) for three different cases: neglecting non-Darcy flow, considering the inertial effect and finally considering water vaporization, respectively.

CONCLUSIONS

• Water vaporization that happens in high-temperature gas reservoirs causes connate water to vaporize near the wellbore.

• At high flow rates in a gas condensate reservoir, non-Darcy flow can impair the productivity index.

• The new water saturation profile imposes an appreciable influence on well behavior. It can change the inertial coefficient β and give rise to an increase in bottom-hole pressure.

• Water vaporization and its follow-up bottomhole pressure improvement can enhance the well productivity index. This must be taken into serious consideration in reservoir studies, especially in hightemperature tight gas condensate reservoirs.

NOMENCLATURE

Greek Letters

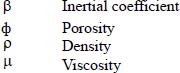
ACKNOWLEDGEMENTS

The authors would like to extend their sincere gratitude to the Reservoirs Systems Engineering Department at National Iranian South Oil Company for their permission to use their CMG software.

APPENDIX 1 Mathematical Model for Water Vaporization in Gas Condensate Reservoirs

There are a few assumptions that were made to develop the model:

1. Water vaporizes in a one-dimensional, radial, homogenous porous medium and three phases (water, gas and condensate) are present.

2. Water can not flow because the reservoir is at initial water saturation.

3. Pressure declines in a pseudo-steady state fashion.

4. Gas production rate and temperature are constant.

5. All phases are in equilibrium.

6. Tuning the parameters of the EOS is made in an attempt to improve prediction accuracy. Start from the continuity equation:

For water ρ is constant (incompressible fluid), therefore:

where C_wg, C_ww and Care mole fractions of water in gas phase, aqueous phase and oil phase, respectively. Since the mobility of the aqueous phase is assumed to be small compared to the mobility of the gas and oil phases, Eq. (2) becomes:

By replacing S_g=1-S_o-S_w, the first term on the left hand side of Eq. (3) changes to:

Using the pseudo-pressure solution for flow of gas through porous media (Dake, 1982):

where Q is the gas flow rate, T is temperature, S is skin and DQ is rate dependent skin.

Taking the derivative of Eq. (A5) with respect to the radius in field units:

Also from the chain rule:

Equating Eq. (A6) and (A7):

Knowing that:

Therefore:

Replacing Eq. (9) in (10):

For the condensate phase, we assume the condensate behaves similar to oil, hence:

By replacing Eqs. (A12) and (A11) in Eq. (A3), Eq. (A13) becomes:

By simplification of Eq. (13):

The above equation is non-linear and must be solved numerically. Using the finite difference approximation for water saturation with a time step of n+1:

NOMENCLATURE

Greek Letters

Figure (A1)
Comparison of GEM and model at 217 °F after 1000 days production.

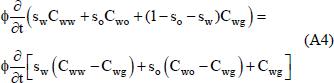
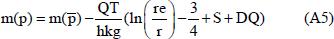
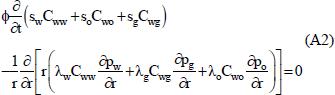
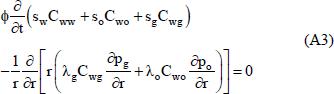
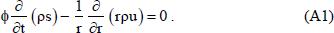
REFERENCES

• Bette, S., Heinemann, R., Compositional modeling of high temperature gas-condensate reservoirs with water vaporization. SPE 18422, Presented at SPE Symposium on Reservoir Simulation, Houston, TX, February 6-8 (1989).
• Coles, M. E. and Hartman, K. J., Non-Darcy measurements in dry core and effect of immobile liquid. Paper SPE 39977 presented at the 1998 SPE Gas Technology Symposium, Calgary, 15-18 March (1998).
• Corey, A. T., The interrelation between gas and oil relative permeabilities. Producers Monthly, 19(1), 38-41 (1954).
• Cornell, D. and Katz, D. L., Flow of gases through consolidated porous media. Industrial & Engineering Chemistry, 45(10), 2145-2152 (1953).
• Dake, L. P., Fundamental of Reservoir Engineering. 5th Ed. Elsevier Science, Amsterdam, the Netherlands (1982).
• Dodson, C., Standing, M., Pressure-volume-temperature and solubility relationships for natural gaswater mixtures. Drilling and Production Practice, American Petroleum Institute (1944).
• Fancher, G. H. and Lewis, J. A., Flow of simple fluids through porous materials. Industrial & Engineering Chemistry, 25(10), 1139-1147 (1933).
• Geertsma, J., Estimating the coefficient of inertial resistance in fluid flow through porous media. Society of Petroleum Engineers Journal, 14(05), 445-450 (1974).
• Grattoni, C., Guise, P., Phillips, G., Fisher, Q., Knipe, R., Evaluation of water evaporation and salt precipitation due to flow in gas reservoirs. International Symposium of the Society of Core Analysts, Noordwijk, The Netherlands 27-30 September (2009).
• Gringarten, A. C., Bozorgzadeh, M., Daungkaew, S. and Hashemi, A., Well Test analysis in lean gas condensate reservoirs: Theory and practice. SPE 100993, paper presented at the 2006 SPE Russian Oil and Gas Technical Conference and Exhibition, Moscow, Russia, 3-6 October (2006).
• Kalaydjian, F. J-M., Bourbiaux, B. J. and Lombard, J-M., Predicting gas/condensate reservoir performance: How flow parameters are altered when approaching production wells. Paper SPE 36715 presented at the 1996 SPE Annual Technical Conference and Exhibition, Denver, Colorado, 6- 9 October (1996).
• Kamath, J., Laroche, C., Laboratory based evaluation of gas well deliverability loss due to water blocking. SPE 63161, Presented at the SPE Annual Technical Conference and Exhibition, Dallas, Texas, October 1-4, (2000).
• Kurihara, M., Liang, J., Fujimoto, F., Nghiem, L. and Sammon, P., Development and application of underground gas storage simulator. SPE 59438, Presented at the Asia Pacific Conference on Modeling for Asset Management, Yokohama, Japan, 25-26 April (2000).
• Lombard, J. M., Longeron, D. G., Influence of connate water and condensate saturation on inertial effect. Paper SCA 9929 presented at 2000 Intl. Symposium of Core Analysts, 1-4 August (2000).
• Mott, R., Engineering calculations of gas-condensate- well productivity. SPE Reservoir Evaluation & Engineering, 6(05), 298-306 (2003).
• Noman, R. and Archer, J. S., The effect of pore structure on non-darcy gas flow in some lowpermeability reservoir rocks. Paper SPE 16400 presented at the 1987 SPE/DOE Low-Permeability Reservoirs Symposium, Denver, Colorado, 18-19 May (1987).
• Peng, D. Y., Robinson, D. B., A new two-constant equation of state. Ind. Eng. Chem. Fundam. 15(1), 59-64 (1976).
• Rajeev, R. L., Well testing in gas condensate reservoirs. M.Sc. Thesis, Stanford University, Department of Petroleum Engineering (2003).
• Tek, M. R., Coats, K. H., Katz, D. L., The effect of turbulence on flow of natural gas through porous reservoirs. Journal of Petroleum Technology, 14 (07), 799-806 (1962).
• Zuluaga, E. and Lake, L. W., Modeling of experiments on water vaporization for gas injection using traveling waves. SPE Journal, 13(02), 248- 256 (2008).
• Zuluaga, E., Lake, L.W., Semi-analytical model for water vaporization in gas producers. SPE 91393, Presented at the SPE Eastern Regional Meeting, Society of Petroleum Engineers, Charleston, West Virginia, 15-17 September (2005).
• Zuluaga, E., Monsalve, J. C., Water vaporization in gas reservoirs. SPE 84829, Presented at the SPE Eastern Regional Meeting, Society of Petroleum Engineers, Pittsburgh, Pennsylvania, 6-10 September (2003).

Publication Dates

• Publication in this collection
  Jan-Mar 2015

History

• Received
  15 May 2012
• Reviewed
  07 Apr 2014
• Accepted
  12 Apr 2014