Effects of an array of widely separated vertical cylinders on time-averaged properties of progressive monochromatic waves

Efeitos de um arranjo de cilindros verticais afastados em propriedades promediadas de ondas progressivas

ABSTRACT

The design of monopile foundations for offshore wind farms, the estimate of wave loads, and the effect of the structures on the environment usually consider one single vertical cylinder. This choice is based on the size of the ratio cylinder diameter to wavelength, and on the large distances between turbines. However, for large arrays of monopiles, the ensemble effect must be investigated. This study addresses monochromatic wave propagation through a rectangular array of four cylinders 800 m and 300 m apart, considered here as the fundamental geometry for an arbitrary array of monopiles turbines. Results for bottom velocities, mean water level, mass transport, and radiation stress tensor in the presence of the array are compared with those for a single cylinder. The numerical model WAMIT® is used to compute the potential velocity solution. Relevant spatial variations were found, especially for radiation stresses, for different periods and directions of propagation. Diffraction effects on the wave field by the array are significantly stronger than the superposition of individual effects of isolated cylinders under the same conditions. Impacts of the entire wind farm on bottom morphodynamics near the foundations, on the design loads, and on the wave climate past the wind farm are discussed.

Keywords:  Wave-cylinder interaction; Monopile array; Radiation stress; Second-order effects; Offshore wind farms

RESUMO

O cálculo das fundações das estruturas de suporte de turbinas (monopilares) de parques eólicos offshore, a estimativa dos esforços causados pelas ondas, e o efeito das estruturas no meio ambiente, costumam considerar estas estruturas como cilindros verticais isolados. Justifica-se esta escolha pelo pequeno valor da razão entre o diâmetro dos monopilares e o comprimento da onda, e pelas longas distâncias entre as turbinas. Contudo, no caso de um grande arranjo de monopilares, o efeito do conjunto deve ser investigado. Este trabalho aborda a propagação de ondas através de um arranjo retangular de quatro cilindros separados 800 m e 300 m, aqui considerada como a geometria básica para um parque offshore de turbinas monopilares de arranjo geométrico qualquer. Resultados para velocidades no fundo, nível médio da água, transporte de massa e tensor de radiação na presença do arranjo são comparados àqueles obtidos com um único cilindro. O modelo numérico WAMIT® é usado para calcular a solução do potencial de velocidades. Os resultados mostram variações espaciais relevantes, especialmente para as tensões de radiação, para diferentes períodos de ondas incidentes e ângulos de propagação. Os efeitos de difração no campo de ondas pelo arranjo de cilindros foi significativamente maior que a superposição dos efeitos de difração de cilindros isolados nas mesmas condições de ondas. Os impactos da difração produzidos pelo conjunto do parque eólico sobre os processos morfodinâmicos no entorno das fundações, sobre as cargas atuantes nas estruturas, e sobre o clima das ondas após a passagem pelo parque são discutidos.

Palavras-chave:  Interação onda-cilindro; Arranjo monopilar; Tensor de radiação; Efeitos de segunda-ordem; Parques eólicos offshore

INTRODUCTION

Policies to reduce carbon emission have changed the world energy matrix, gradually substituting fossil fuel sources by renewable ones: the use of offshore wind energy has rapidly grown during the last two decades as being a viable option (Breton & Moe, 2009). By the end of 2018, the total offshore wind power capacity installed worldwide was 23.14 GW (Global Wind Energy Council, 2019). Most of the offshore wind energy has been installed in the northern European waters, currently representing 79% of the total installed capacity. The remaining 21% is mostly installed in the Asia-Pacific area. However, a broader distribution among other areas of the world is expected to happen in the next years. Like several other nations, Brazil has specific offshore plans for the next coming years. Soon, as offshore wind energy plays an important role in energy supply, it is necessary to improve the methodologies for environmental impact assessment and monitoring. This is particularly important as the number of turbines installed in wind farms has also significantly increased.

In 2018, the largest wind farms in generated power were Walney Extension-UK, with 659 MW and 87 monopile turbines (Ørsted, 2017), London Array-UK, with 630 MW and 175 monopile turbines (Vanhellemont & Ruddick, 2014), and Gemini Wind Farm-NL, with 600 MW and 150 monopile turbines (Brasseur et al., 2018). Installed offshore wind turbines use various design configurations such as jackets, gravity foundations, or floating structures. The most common solution for shallow waters, up to 25-30 m, is monopile (Wei et al., 2014). Little attention is given to the occupied area of these large offshore wind farms. The existing literature on how large wind farms affect wave climate is still limited, although several authors have addressed the impacts on the ecosystem (Tucker, 1996), on local meteorology (Baidya Roy et al., 2004; Hasager et al., 2015), and on the ocean (Segtnan & Christakos, 2015; Cazenave et al., 2016).

Distances between turbines ($d$) vary normally from 150-400 m in the wind dominant direction and 500-1200 m in the perpendicular wind dominant direction, and this distance is chosen relative to the rotor diameter size. For a fixed geometry, changes in wave periods will result in different wave lengths $\left(L\right)$ and, consequently, relative distances $d/L$ will change. Therefore, waves will sense the monopile array geometry according to the frequencies of the sea state. The monopile can be simulated as a vertical cylinder with diameter $\left(D\right)$ within the range of 5-10 m. In comparison to typical wave lengths, of the order of 10² m, the cylinder diameter is small $\left(D/L\le 0.2\right)$.

The relative size of the cylinder with respect to the incident waves $\left(D/L\right)$ and the Keulegan-Carpenter number $\left(KC\right)$ determine the kind of interaction between waves and vertical circular cylinders. The $KC$ represents the relation between the excursion length of the fluid particles and the size of the flow obstacle in the direction of the wave propagation. It measures the importance of drag forces relative to inertial forces. For vertical circular cylinders, it is expressed as $KC=uT/D$, where $u$ is the amplitude of the horizontal fluid velocity and $T$ is the wave period (Sumer & Fredsøe, 1997). Regarding diffraction effects for far apart isolated cylinders, when $d/L>1$, drag forces dominate and diffraction is less important when $D/L\le 0.2$ (Vepa, 2013). In this case, forces on the structure can be calculated using the velocity field for the incident waves (Kim & Chen, 1994). Consequently, the interaction between waves and monopiles has been traditionally approached considering extreme incident waves and one single monopile. However, a large number of monopiles may generate a diffraction pattern different from the local, and relatively non relevant, diffraction effect of one single monopile, even for $d/L>1$, thus affecting velocities, accelerations and forces acting on the monopiles. The monopile array may also be capable of modifying the incident wave pattern that goes through the wind farm and reaches the nearby coast.

The interaction between waves and a cylindrical structure has been investigated for decades, since the pioneering studies by Havelock (1940), who obtained an exact analytical solution for the diffraction of linear waves by a single cylinder in infinite water depth, and by MacCamy & Fuchs (1954), who extended the theory for the case of finite water depth. After these studies, numerous authors worked to obtain a direct second order solution (e.g. Kim, 1988; Kriebel, 1990, 1992), or compute the second order hydrodynamic loads using an indirect approach (Molin, 1979; Chau & Taylor, 1992; Taylor & Huang, 1997). The introduction of numerical schemes and Green's functions have been used to obtain second-order wave elevation and pressure loads for monochromatic, bichromatic and random waves (Kim, 1988; Kim & Yue, 1989, 1990; Kareem et al., 1994).

The interaction between waves and arrays of vertical cylinders has also been investigated by many authors (Spring & Monkmeyer, 1974; Kagemoto & Yue, 1986; Abul-Azm & Williams, 1989; Linton & Evans, 1990; Ghalayini & Williams, 1991; Moubayed & Williams, 1995) and an extensive review on this subject was conducted by McIver (2002). More recently, Huang (2004), Walker & Taylor (2005), Wang & Wu (2007), and Steward (2018), have studied arrays of 2, 4 and 25 cylinders separated by short distances, $d/L<1$.

Experimental studies about one or more cylinders have been conducted by Ohl et al. (2001a, 2001b), Kagemoto et al. (2002), Kagemoto et al. (2014), and Kamra et al. (2019), among others. Kagemoto et al. (2002) studied regular wave interaction with an array of 50 truncated cylinders, and Kagemoto et al. (2014) presented experimental results of the first and second-order free surface displacements between two rows of vertical cylinders. Lately, the introduction of Computational Fluid Dynamics (CDF) has allowed to solve the wave diffraction around a cylinder or a small group of cylinders with a very detailed description of the physical processes as the fluid physics are computed with a few assumptions (Kamath et al., 2016; Bihs et al., 2017; Mohseni et al., 2018).

Research on the subject of wave-cylinder interaction in the last decades, driven mostly by demands of the offshore oil industry, have provided an extensive knowledge of wave forces, run-up, the resulting free surface field, and the conditions and implications of near-trapping phenomenon for cylinders a few diameters apart from each other. Since Sharma & Dean (1981), little attention has been given to the velocity field and time averaged second order quantities which are derived from linear theory results such as mean water level, mass transport, and radiation stress (Dean & Darlymple, 1991). Besides, the growth of the offshore wind energy has risen some issues that require further study. First, previous investigations on arrays of vertical cylinders have focused on the case of cylinders separated by short distances $(d/L<1)$. Second, the literature on the diffracted velocities for arrays of widely separated cylinders is, to the authors’ knowledge, inexistent. Third, although the effect of offshore wind farms on the wind field has been extensively investigated, their effects on waves, morphological processes around the structures, and littoral processes and nearshore hydrodynamics are still ongoing basic research topics.

Taking a small array of four cylinders, which could be considered as the basic unit of a monopile offshore wind farm, it seems that they can induce significant changes as to be necessary to consider the whole monopile turbine array for environmental assessments and design purposes.

The present investigation aims at verifying whether the diffraction effects on the wave field by an array of far apart cylinders $(25>d/L>1)$ can be studied as the effect of isolated cylinders or if the scattered waves generated by each cylinder interact with each other and the array must be studied considering all the cylinders.

This paper presents the results of wave-cylinder interaction for bottom velocities, mean water level, depth averaged mass transport, and radiation stress field for an array of four cylinders separated by distances of the order of $16>d_x/L>7$ and $6>d_y/L>2.6$, where $d_x$ and $d_y$ are the distances between turbines along the $x$ and $y$ axes, respectively, and compares these results with those obtained for one isolated cylinder. The effect of the incident wave period and propagation angles has also been studied.

MATERIAL AND METHODS

This section includes a review of the linear theory for wave-cylinder diffraction, and the second-order time averaged properties (mass transport, mean water level and radiation stresses) obtained from linear theory. From MacCamy & Fuchs (1954) analytical solution for the velocity potential of diffracted waves by one cylinder, the analytical expressions of velocities and mean water level are derived.

Wave-cylinder diffraction

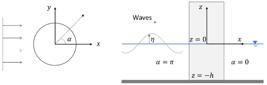
Consider a monochromatic wave of height $H$ and angular frequency $\omega$, propagating at uniform water depth $h$ in the positive $x$ direction, as shown in Figure 1. The formulation of the diffraction problem by one single vertical cylinder of radius $a$ assumes ideal incompressible fluid and irrotational flow, the fluid velocity is represented by the gradient of a scalar velocity potential, $\varphi \left(r,\alpha ,z,t\right)$, which is the solution of Laplace's equation in the fluid domain in cylindrical coordinate, Equation 1.

Figure 1
Variables definition scheme for the case of one isolated cylinder.

${\varphi }_{rr}+\frac{1}{r}{\varphi }_r+\frac{1}{r^2}{\varphi }_{\alpha \alpha }+{\varphi }_{zz}=0$ (1)

The total diffracted velocity potential is the sum of the incident ${\varphi }^i$ and the scattered velocity potential ${\varphi }^s$. Assuming small amplitude waves, the velocity potential can be expanded in a perturbation series in terms of the wave steepness $\epsilon =H/L$, where $H$ is the wave height. The boundary value problem, with the appropriate conditions at the bottom, at the free surface, around the cylinder, and the radiation condition in the far field, is expressed as Equation 2.

$\left.\begin{array}{c}{\nabla }^2\varphi =0\\ {\varphi }_z=0atz=0\\ {\varphi }_{tt}+g{\varphi }_z=0atz=0\\ {\varphi }_r=0atr=a\\ \underset{r\to \infty }{\lim }{r}^{1/2}\left({\varphi }_r^s-ik{\varphi }^s\right)=0\end{array}\right\}$ (2)

The radiation condition imposes that the wave energy associated with the disturbance due to the presence of the cylinder is carried away from the body in all directions in the far field. The general first order solution in cylindrical coordinates $\left(r,\alpha ,z,t\right)$ was given by MacCamy & Fuchs (1954) in Equation 3, where $H_m^{\left(1\right)}$ and $J_m$ are the Hankel and Bessel functions of the first kind and $m$ order, and the prime denotes the derivative relative to the argument of these functions (in this case, the radial distance). The wave number $k$ is given by the dispersion relationship $k\tanh \left(kh\right)={\omega }^2/g$, where $g$ is the gravity acceleration constant.

$\begin{array}{l}\varphi \left(r,\alpha ,z,t\right)=\text{Re}\left\{{\phi }_1\left(z\right){\phi }_2\left(t\right){\phi }_3\left(r,\alpha \right)\right\};\\ {\phi }_1\left(z\right)=\frac{gH}{2\omega }\frac{\cosh \left(\left.k(h+z\right)\right)}{\cosh \left(kh\right)},\\ {\phi }_2\left(t\right)=e^{-i\omega t},\\ {\phi }_3\left(r,\alpha \right)={\Psi }_0+2\left({\displaystyle \sum }_{m=1}^{\infty }{i}^m{\Psi }_m\cos \left(m\alpha \right)\right),\\ {\Psi }_m=J_m\left(kr\right)-\frac{J_m^{\text{'}}\left(ka\right)}{H_m^{\left(1\right)\text{'}}\left(ka\right)}{H}_m^{\left(1\right)}\left(kr\right)\end{array}$ (3)

The formulation of the diffraction problem for arrays of vertical cylinders is similar to what has been presented in this section for the case of one cylinder. Although, the total velocity potential is now the sum of the velocity potential of the incident waves and the scattered waves due to the presence of all the bodies that form the array. In this study, the computer program WAMIT® (WaveAnalysisMIT) is used to solve the diffraction boundary value problem to obtain the time harmonic solutions of the first term of the series expansion for a specific incident wave field. WAMIT® has been widely used in the offshore and naval industry, but it has also been adopted in some recent studies to the case of vertical cylinders in the field of coastal engineering and studies of wind farms (Christensen et al., 2014; Newman, 2014; Mohseni et al., 2018; Read et al., 2018).

To solve the diffraction problem by the integral method, the boundary value problem of Equation 2 is rewritten in integral equations form, using the wave source potential as a Green function. In a Cartesian coordinate system, where ${\rm X}=\left(x,y,z\right)$, the velocity potential can be expressed as Equation 4.

$\varphi \left({\rm X},t\right)=\text{Re}\sum {\varphi }^d\left({\rm X}\right)e^{i\omega t}$ (4)

Equation 5 (Korsmeyer et al., 1988) shows the corresponding expression for the diffraction potential ${\varphi }^d$, where $S_B$ denotes the cylinder boundary, $n$ is the vector normal to the body boundary, and $G\left(\xi ;{\rm X}\right)$ is the Green function (the velocity potential at the point ${\rm X}$ due to the source of strength located at the point $\xi$), based on Bessel function of zero order that satisfies the free-surface condition.

$2\pi {\varphi }^d\left({\rm X}\right)+{{\displaystyle \iint }}_{S_B}{\varphi }^d\left(\xi \right)\frac{\partial G\left(\xi ;{\rm X}\right)}{\partial n_{\xi }}d\xi =4\pi {\varphi }^i\left({\rm X}\right)$ (5)

Next, the integral equations are solved using a ‘panel’ method. In this method, the wetted surface of the body is represented by an ensemble of quadrilateral panels. The obtained linear system is, finally, solved by an iterative method to obtain the unknown velocity potential and the source strength on the cylinder surface. After this, the fluid velocity on the cylinder surface is evaluated.

WAMIT® provides the results for the real and imaginary parts of the dynamic pressure and the Cartesian components of the velocity field, at any point of the fluid domain. From these quantities, the time series of the pressure and the velocities are easily computed as shown in Equation 6, where ${\rm N}$ is a complex variable, whose real and imaginary parts are ${\text{N}}_r$ and ${\text{N}}_i$, respectively, and it can represent either the dynamic pressure, $p$, or the Cartesian components of the vector velocity, $\left(u,v,w\right)$. The free surface elevation is directly obtained from the dynamic pressure at the still water level.

$${\rm N}\left(x,y,z,t\right)=\mathrm{Re}\left\{\left({{\rm N}}_r+i{{\rm N}}_i\right)e^{i\omega t}\right\}$$ (6)

Mass transport

Surface gravity waves induce a periodic motion to fluid particles. According to linear theory for monochromatic progressive waves, the Lagrangean particle trajectories are closed ellipses. In reality the oscillatory motion is not completely ‘closed’, though, and a net drift in the direction of wave propagation, known as the Stokes drift, is produced (Stokes, 1880). The Stokes drift can be seen as the difference between the average Lagrangean flow velocity of a fluid parcel and the average Eulerian flow velocity of the fluid and can be calculated as Equation 7 (Van Den Bremer & Breivik, 2018).

$V_{SD}=\overline{{\delta }^{\left(1\right)}\cdot \nabla V^{\left(1\right)}}$ (7)

where $V^{\left(1\right)}$ is the first order in wave steepness velocity field at the mean water level; and ${\delta }^{\left(1\right)}$ is the first order in wave steepness linear displacement vector.

Since Stokes drift can be understood as the vertical distribution of mean wave momentum per unit volume, a new quantity can be defined which corresponds to the depth-integrated Stokes drift, also known as Stokes transport. The time averaged, depth integrated net mass transport per unit length of wave crest and per unit is given by the Stokes transport multiplied by the water mass density $\rho$. Equations 8 and 9, (Longuet-Higgins, 1969), give the projection of the mass transport in the $x$ and $y$ directions as a function of the instantaneous water level, $\eta$, and the velocity components.

$M_x=\rho {\left.\overline{\eta u}\right|}_{z=0}$ (8)

$M_y=\rho {\left.\overline{\eta v}\right|}_{z=0}$ (9)

For regular periodic waves propagating in any given direction defined by the unit vector $n=\left(\cos \theta ,\sin \theta \right)$, the mass transport in this direction is expressed as in Equation 10, where $c$ is the wave phase speed and $E$ is the wave energy density per unit area. For a fixed wave height, the smaller the wave period, the stronger the mass transport.

$\left|M\right|=\frac{1}{8}\rho g{H}^2\frac{k}{\omega }=\frac{E}{c}$ (10)

From WAMIT® results for the free surface, $\eta =Re\left\{\left({\eta }_r+i{\eta }_i\right)e^{i\omega t}\right\}$, and for horizontal velocities $u$ and $v$, the mass transport can be computed by Equations 11 and 12.

$M_x=\rho \overline{\eta u}=\frac{1}{2}\rho \left({\eta }_r{u}_r+{\eta }_i{u}_i\right)atz=0$ (11)

$M_y=\rho \overline{\eta v}=\frac{1}{2}\rho \left({\eta }_r{v}_r+{\eta }_i{v}_i\right)atz=0$ (12)

Quantifying Stokes drift and mass transport is important for nearshore circulation, as they affect the wave-induced sediment transport and sandbar migration (Van Den Bremer & Breivik, 2018). When surface waves propagate normal to the shore, the Stokes drift produces an accumulation of water in the surf zone, which in turn builds up a pressure gradient which originates an offshore flow (undertow). Mass transport also plays an important role, in combination with Eulerian currents, transporting tracer substances, floating objects and fluid, such as micro-plastics and oil films in the upper ocean layer.

In case of wave breaking within the offshore wind farm, the pattern of mass transport would play an important role on bottom evolution. Otherwise, oil spills may also occur in the monopiles surrounding waters and may generate pollution with plastic debris during maintenance works. Therefore, studying mass transport is relevant for wind farms environmental assessments.

Mean water level

As surface gravity waves approach the coast, they become shorter, steeper, and eventually break. After breaking, they keep moving forward to the beach with decreasing height, thus affecting the momentum flux and introducing changes in radiation stress and the mean water level. Negative and positive changes, usually called set-down and set-up, occur before and after the breaking point, respectively.

Wind farms are commonly installed in intermediate water depths, before the wave breaking point. In this case, the mean water level at the wind farm location will experience a set-down. For regular periodic progressive waves, Longuet-Higgins & Stewart (1962) obtained the expression of wave set-down, Equation 13.

$\overline{\eta }=-\frac{1}{8}\frac{H^{2}k}{\sinh \left(2kh\right)}$ (13)

Wave diffraction by vertical cylinders modifies the pattern of the incident waves. Larger wave heights occur near the cylinder and areas with smaller wave heights might appear inside the array due to negative interferences (Wang & Wu, 2007). As a result, mean water level will be modified from the theoretical set-down that is associated with the periodic regular waves that are approaching the cylinders, Equation 13.

To obtain the expression of the mean water level around one or more cylinders, the expression has been derived from Bernoulli’s equation, Equation 14.

${\varphi }_t+\frac{1}{2}\left({\varphi }_x{}^2+{\varphi }_y{}^2+{\varphi }_z{}^2\right)+g\eta =B\left(t\right)atz=\eta$ (14)

Considering Bernoulli’s constant $B\left(t\right)=0$, the general expression of the mean water level is obtained by following these steps: (1) taking Taylor’s expansion at $z=0$; (2) retaining only the terms up to second order $O{\left(kH\right)}^2$, and; (3) time averaging in wave period. After these steps, the expression of the mean water level can be written as in Equation 15.

$\overline{\eta }=-\frac{1}{g}{\left.\overline{\eta {\varphi }_{tz}}\right|}_{z=0}-\frac{1}{2g}{\left.\overline{\left({\varphi }_x{}^2+{\varphi }_y{}^2+{\varphi }_z{}^2\right)}\right|}_{z=0}$ (15)

The analytical expression for the mean water level for the case of one cylinder is derived. Considering ${\phi }_2\left(t\right)=\cos \left(\omega t\right)-i\sin \left(\omega t\right)$, and the real and imaginary part of ${\phi }_3$ as $P$ and $Q$, respectively, so ${\phi }_3$ can be written as ${\phi }_3\left(r,\alpha \right)=P+iQ$, the expression of the mean water level can be written as Equation 16, where $K$ is $k\tanh \left(kh\right)$, and $P_r,Q_r,P_{\alpha },Q_{\alpha }$ are the radial and alpha derivatives of the real and imaginary part of ${\phi }_3$, respectively.

$\overline{\eta }=\frac{H^2}{8}\left[K\left(P^2+Q^2\right)+\frac{g}{2{\omega }^2}\left(P_r{}^2+\frac{1}{r^2}{P}_{\alpha }{}^2+P^2+Q_r{}^2+\frac{1}{r^2}{Q}_{\alpha }{}^2+K^2{Q}^2\right)\right]$ (16)

From WAMIT® results, the mean water level is calculated by Equation 17.

$\overline{\eta }=\frac{1}{2g}\left[\omega \left({\eta }_r{w}_i-{\eta }_i{w}_r\right)-\frac{1}{2}\left(u_r{}^2+u_i{}^2+v_r{}^2+v_i{}^2+w_r{}^2+w_i{}^2\right)\right]atz=0$ (17)

The computation of the mean water level within arrays of vertical cylinders far apart provides information about the multiple interaction of the scattered wave produced by each cylinder. In addition, calculating the mean water level is necessary to compute radiation stress.

Radiation stress

The definition of the radiation stress tensor was first introduced by Longuet-Higgins & Stewart (1962), and physically discussed in (Longuet-Higgins & Stewart, 1964). The radiation stress is the depth-integrated – and thereafter phase-averaged – excess of momentum flux on the mean flow caused by the presence of surface gravity waves. It describes the additional forcing due to the presence of the waves. Spatial gradients in radiation stresses produce changes in the mean water level and generate a mean flow.

The general expressions for the second-order components of the radiation stress tensor, $S_{ij}$, are given by Equation 18, where $u$ is the horizontal velocity, $p_t$ is the total pressure term, ${\delta }_{ij}$ is the Kronecker delta, the $i$ and $j$ subscripts correspond to the Cartesian components $x$ and $y$, respectively, and the overbar means time averaging.

$S_{ij}=\overline{{{\displaystyle \int }}_{-h}^{\eta }\rho u_i{u}_j+p_t{\delta }_{ij}dz}-\frac{1}{2}\rho g{\left(h+\overline{\eta }\right)}^2$ (18)

For progressive monochromatic waves propagating at an angle $\theta$ relative to the coordinate $x-y$ system, the expressions of the radiation stress tensor components are given by Equations 19 to 21, where $n$ is the ratio of group velocity to wave celerity, given by Equation 22.

$S_{xx}=E\left[n\left({\cos }^2\left(\theta \right)+1\right)-\frac{1}{2}\right]$ (19)

$S_{yy}=E\left[n\left({\sin }^2\left(\theta \right)+1\right)-\frac{1}{2}\right]$ (20)

$S_{xy}=\frac{E}{2}n\sin \left(2\theta \right)$ (21)

$n=\frac{1}{2}\left(1+\frac{2kh}{\sinh \left(2kh\right)}\right)$ (22)

When a progressive wave train finds an obstacle, it is partially reflected, and the momentum reverses its initial direction. For momentum conservation, the obstacle experiences a force equal to the rate of change of the wave momentum. The force acting on the body is a manifestation of the radiation stress. Analogously, one might consider what happens to the whole ensemble of structures, like the monopile array. Changes on the radiation stress around an array of vertical cylinders will induce different forces on the individual structures. Besides, radiation stresses are fundamental to characterize important mechanisms of sediment transport at the bottom of the array and in shallow regions.

To compute the radiation stresses from WAMIT® results, the expressions of $S_{ij}$ have been derived from the general expression in Equation 18. The vertical dimension of the fluid domain is discretized in $\Delta z$ equal increments. After some algebraic calculations, the resulting expressions are given by Equation 23 to 25, where $\left|*\right|$ denotes the modulus of the complex amplitude and the series correspond to the numerical integration in $z$, using the trapezoidal rule.

$\begin{array}{l}{S}_{xx}=-\frac{1}{4}\rho g{\left|\eta \right|}^2+\frac{1}{2}\left(p_r{}_{\left|z=0\right.}{\eta }_r+p_i{}_{\left|z=-h\right.}{\eta }_i\right)-\frac{1}{2}\rho \Delta z\left(\frac{{\left|w_{\left|z=0\right.}\right|}^2}{2}+\frac{{\left|w_{\left|z=-h\right.}\right|}^2}{2}+\sum {\left|w\right|}^2\right)+\\ \frac{1}{2}\rho \Delta z\left(\frac{{\left|u_{\left|z=0\right.}\right|}^2}{2}+\frac{{\left|u_{\left|z=-h\right.}\right|}^2}{2}+\sum {\left|u\right|}^2\right)\end{array}$ (23)

$\begin{array}{l}{S}_{yy}=-\frac{1}{4}\rho g{\left|\eta \right|}^2+\frac{1}{2}\left(p_r{}_{\left|z=0\right.}{\eta }_r+p_i{}_{\left|z=-h\right.}{\eta }_i\right)-\frac{1}{2}\rho \Delta z\left(\frac{{\left|w_{\left|z=0\right.}\right|}^2}{2}+\frac{{\left|w_{\left|z=-h\right.}\right|}^2}{2}+\sum {\left|w\right|}^2\right)+\\ \frac{1}{2}\rho \Delta z\left(\frac{{\left|v_{\left|z=0\right.}\right|}^2}{2}+\frac{{\left|v_{\left|z=-h\right.}\right|}^2}{2}+\sum {\left|v\right|}^2\right)\end{array}$ (24)

$S_{xy}=\frac{1}{2}\rho \Delta z\left(\frac{{\left(u_r{v}_r+u_i{v}_i\right)}_{\left|z=0\right.}}{2}+\frac{{\left(u_r{v}_r+u_i{v}_i\right)}_{\left|z=-h\right.}}{2}+\sum \left(u_r{v}_r+u_i{v}_i\right)\right)$ (25)

SIMULATIONS SET-UP

To verify the importance of diffraction effects on the wave field by cylinders far apart $(d/L>1)$, a set of simulations have been conducted using the diffraction program WAMIT®. In this paper, two scenarios were considered: one cylinder (N1) and an array of four cylinders (N4), both for different combinations of wave period and propagation direction. Table 1 lists the wave properties and the values of important wave-geometric relations for the diffraction problem, for both scenarios, considering 10 m water depth. The symbols have been previously defined.

Table 1
Wave properties and values of the most relevant diffraction wave-geometric relations that influence the studied problem. Note that $T$ is the wave period, $H$ is the wave height, $\theta$ is the wave propagating angle, $L$ is the wave length, $KC$ is the Keulegan-Carpenter number, $D$is the cylinder diameter, and $d_x$-$d_y$are the distances between cylinders in the x-y directions.

$T\left(s\right)$	$H(m)$	$\theta \left(°\right)$	$KC$	$D/L$	$d_x/L$	$d_y/L$
6	1	[0,15,30,45]	0.36	0.20	16.53	6.20
12	1	[0,15,30,45]	0.62	0.09	7.06	2.65

Figure 2 shows the geometrical configurations. The distances between the cylinders $\left(d_x,d_y\right)$, the cylinder diameter $\left(D\right)$, and the depth $\left(h\right)$, are representative of monopile wind farms. Note that for the N4 case, different propagation angles imply that the wave crest is going to be diffracted by structures separated by different distances. Further, the phase of the wave when encountering the cylinder will be different if compared with the same period simulation but different propagation angle.

Figure 2
Scheme of the Cartesian coordinates origin, wave propagation, cylinder positions and results area for the case of one cylinder and four cylinders array. For all simulations, the origin of the z-axis is in the position of the still water level, water depth is 10 m, and the radius of the cylinders is 5 m ($D=10\text{m}$).

Data of the velocity and pressure field have been collected within the shaded area shown in Figure 2, with a spatial discretization of $\Delta x=2\text{m}$, $\Delta y=2\text{m}$ and $\Delta z=1\text{m}$.

The simulations carried out in this study allow to investigate: (1) the effect of introducing four cylinders separated a few hundred meters from each other with relatively small radius, if compared with the diffraction effect of one isolated cylinder; (2) the influence of the wave period in the diffraction interferences in arrays of widely separated cylinders; and, (3) how modifications of wave angles, hence different perturbation patterns, affect the resulting diffracted wave field.

Data analysis validation

To validate the method of data analysis and the derived expressions for the second-order properties addressed in this paper, monochromatic waves with the same periods and angles of propagation listed in Table 1, were also simulated with WAMIT® (case N0). The results of the velocities at the bottom, the mean surface level, the mass transport, and the radiation stress were successfully validated with the theoretical values. The results from Equation 17 for N1 were compared with the results obtained with Equation 16, derived from the solution of MacCamy & Fuchs (1954).

RESULTS AND DISCUSSION

Results for the bottom velocity field, mass transport, mean water level, and radiation stress components are shown in this section. In all illustrations in this section, wave propagates from left to right.

Bottom velocity field

This section presents the spatial distribution of the modulus of the bottom velocity at $t=0\text{s}$, and the amplitude of the velocity field at the bottom. This means that, if $\text{N}$ represents the components of the vector velocity $\left(u,v\right)$ in Equation 6, the amplitude of the velocity for each component is given by Equations 26 and 27.

$u_A=\sqrt{u_r{}^2+u_i{}^2}$ (26)

$v_A=\sqrt{{\upsilon }_r{}^2+{\upsilon }_i{}^2}$ (27)

Thus, the amplitude of the velocity field is given by Equation 28.

$Amp.V_{x,y}=\sqrt{u_A{}^2+v_A{}^2}$ (28)

Figure 3 shows the results for the case of one isolated cylinder. Observing the results for the modulus of the bottom velocity for $T=6\text{s}$, the impact due to the presence of the cylinder is evident. The diffracted velocities have velocity gradients at the same wave phase. These gradients are higher on the up-wave face of the cylinder. The effect of incrementing the wave period is clear. For $T=6\text{s}$, $D/L=0.204$, the limit at where the diffraction effects are relevant, whereas for $T=12\text{s}$, $D/L=0.088$, and the scattered wave produced by the presence of the cylinder does not affect significantly the incident wave field, as expected.

Figure 3
Velocity modulus and velocity amplitude around one cylinder for incident waves of $T=\left[6\text{s},12\text{s}\right]$ and $\theta =0°$.

For the case of $T=6\text{s}$, the amplitudes of the bottom velocity in Figure 3 show a pattern with half the wave length of the incident wave, in front of the cylinder. The presence of a standing wave causes increments of velocity amplitudes from 113%-132% and decreases of 84%-71% at approximately 150 m updrift the cylinder. Behind the structure, two areas of lower velocity amplitudes appear. They result from the destructive interaction between the scattered wave and the progressive incident waves, due to their phase differences. For the case of $T=12\text{s}$, the presence of the cylinder affects the velocity amplitudes near the structure, within the range of 18 m, with smaller/higher velocity amplitudes in the parallel/perpendicular direction of wave propagation.

For the N4 case, Figure 4 represents the modulus of the velocities at the bottom (bottom speed) and the velocity amplitude. Again, the diffraction effects on velocities for the case of $T=12\text{s}$ are restricted to the near field around the cylinders. For $T=6\text{s}$, the results of velocity modulus and velocity amplitude show a rhomboid pattern of high and low velocities due to the diffraction interactions between the four cylinders. The influence of the propagation angle in the resulting velocity field at the bottom is evident when comparing the results for $\theta =0°$ and $\theta =45°$. Different angles of propagation mean that the incident waves will encounter the cylinders at different phases. Consequently, the patterns of velocity modulus and velocity amplitude change, and the location of the maximum velocity amplitudes will be different. For the case of $T=6\text{s}$, when diffraction interaction between cylinders is important, the effect of the upstream side of the array is noticeable, as if the wave sensed the array before reaching it.

Figure 4
Velocity modulus and velocity amplitude around the array of four cylinders for incident waves of $T=\left[6\text{s},12\text{s}\right]$ and $\theta =\left[0°,45°\right]$.

Mass transport

Equation 11 and 12 allows computing the Cartesian components of the mass transport for any linear theory results of pressure and velocity field obtained from WAMIT®.

Figure 5 shows the results for N1 and N4 cases, for wave periods $T=6\text{s}$ and $T=12\text{s}$, and propagation angle $\theta =0°$. For $T=12\text{s}$, mass transport is only affected by the cylinders approximately 20-30 m around the structure, and the results for one or four cylinders are essentially the same. For $T=6\text{s}$, however, the presence of one or four cylinders perturbs the value of the mass transport. Again, as in the analysis of the bottom velocities, it can be observed the diffraction interactions between all the cylinders. Nevertheless, for mass transport results, the presence of the cylinders is noticeable essentially on the lee side of the cylinder.

Figure 5
Mass transport around one isolated cylinder and an array of four cylinders for incident waves of $T=\left[6\text{s},12\text{s}\right]$ and $\theta =0°$. For each case, it is included at right a detailed figure of the mass transport around the cylinder located at $\left(\mathrm{400,400}\right)$, including arrows that indicate mass transport direction.

The mass transport directions for the entire domain does not suffer significant modifications at points located more than 20-30 m away from the cylinders. Therefore, considering the entire domain, the direction of the mass transport would be approximately the same as that of the incident waves.

Behind the cylinders, mass transport is reduced by approximately 80% for all periods and angles simulated in this study. At this location, vortex shedding is important in the wave period scale. If oil or debris spill in this area, it would stay longer than it had occurred elsewhere due to the reduced mass transport capacity. Hence, the changes produced by the cylinders in the mass transport are important and worthy to be analyzed.

Mean water level

Mean water level can be computed from WAMIT® pressure and velocity data using Equation 17. Figure 6 shows the results obtained for one isolated cylinder and an array of four cylinders for propagating waves along the x-axis, for $T=6\text{s}$ and $T=12s$.

Figure 6
Mean water level around one isolated cylinder and an array of four cylinders for incident waves of $T=\left[6\text{s},12\text{s}\right]$ and $\theta =0°$.

As it was observed in the bottom velocities, the presence of the structure modifies the mean water level of the incident wave field before encountering the cylinder(s). This is, again, a consequence of the interaction between the progressive and the scattered waves ahead of the structures. Due to reflection in front of the cylinders, the mean water level is always higher, for all cases. For N4 scenario in case of $T=6\text{s}$, the mean water level increases by 2 cm approximately in front of the first row of cylinders. Since the mean water level is related to the square of the wave height $H$, for wave heights of 3 m, mean water level would increase 20 cm. This fact brings important consequences on computing the loads on the monopiles; therefore the mean water level due to the diffraction effects should not be neglected.

Radiation stress

Although the theoretical expression for the radiation stresses, Equation 18, include the mean water level, after some algebraic work the expressions of the radiation stress components from WAMIT® data, Equations 23 to 25, do not include explicitly the mean water level. Yet, the results obtained in this study demonstrate clearly some relation between mean water level and radiation stresses. Spatial gradients in mean water level would force spatial gradients on the radiation stresses, which in turn drives mean currents. Figure 7 to Figure 9 show the results of the radiations stresses. The results for $S_{xx}$, $S_{yy}$, $S_{xy}$ are displayed using different color scales in each figure to avoid misinterpretation.

Figure 7
Radiation stress components around one cylinder for incident waves of $T=\left[6\text{s},12\text{s}\right]$ and $\theta =0°$.

Figure 9
Radiation stress components around an array of four cylinders for incident waves of $T=\left[6\text{s},12\text{s}\right]$ and $\theta =45°$.

For the N1 case, Figure 7, the introduction of the structure in a progressive wave field produces significant perturbations on the radiation stresses components in the entire modelling domain, these variations being greater near the structure. As an example of the magnitude of the variations near the cylinder, comparing with the corresponding values of $S_{xx}$ without structures, $S_{xx}$ is within 152%-76% for $T=6\text{s}$, and 122%-78% for $T=12\text{s}$. It is important to note that the diffraction effects induce radiation stresses for $S_{xy}$, that otherwise would be constant for monochromatic waves.

For the N4 case, Figure 8 and Figure 9, the resulting radiation stress field is the consequence of the interaction processes between all the diffracted/scattered waves. The magnitude of the fluctuations remains significant at hundreds of meters away from the cylinders. Comparing different wave propagation angles, Figure 8 and Figure 9, the resulting radiation stress field is substantially different. Therefore, it can be deduced that the radiations stress field depends on the relative position between the cylinders, the number of cylinders that interacts with the same crest, and the wave phase at which those interactions occur.

Figure 8
Radiation stress components around an array of four cylinders for incident waves of $T=\left[6\text{s},12\text{s}\right]$ and $\theta =0°$.

The radiation stress field around the cylinder that propagates away from the array is clearly modified from the incident one that reaches initially the group of cylinders. Therefore, the wave forces on the cylinders and the hydrodynamic processes around the structures would be altered.

Another consequence is that the entire wave field, after crossing the wind farm, should be altered. Therefore, the momentum flux which would reach the shore, should be different from that if the wind farm were not present. This is certainly an important finding, not much cited in the literature regarding environmental impact assessments of wind farms (Christensen et al., 2014), with the advantage that the method herein described in this paper provides an objective way of computing the overall effect of a wind farm on the wave field, through the computation of the modified field of the radiation stress tensor.

CONCLUSION

Numerous investigators have addressed the interaction between waves and cylinders. Nevertheless, the knowledge about how groups of cylinders, which are more than one wave length apart $(d/L>1)$, as monopile turbines in offshore wind farms, affect the incident wave field is still limited. The present work investigated the interaction between monochromatic waves and: (1) one isolated cylinder; and (2) an array of four cylinders distant between 1 and 25 wave lengths from each other.

From the analytical solution for one cylinder, the analytical expressions for the velocities and the mean water level were derived. The expressions to compute mass transport, mean water level, and radiation stresses from WAMIT® data, were also obtained. Using the numerical wave-diffraction program WAMIT®, results were presented for one isolated cylinder and for an array of four cylinders (the assumed basic cell for offshore wind farms). The cylinders of the array were separated $d_x=800\text{m}$ and $d_y=300\text{m}$. Different combinations of wave periods $\left(T=6\text{s},T=12\text{s}\right)$ and wave propagation angles $\left(\theta =0°,\theta =45°\right)$ were studied. Results from analytical expressions and theoretical results for monochromatic progressive waves were employed to verify the expressions and data analyses used with WAMIT® data.

The results for bottom velocities, mass transport, mean water level and radiation stresses of one isolated cylinder (N1) and the array of four cylinders (N4) were compared. It was verified that the N4 case shows an ensemble effect, which corresponds to the interaction of the incident wave field with all the cylinders of the array. The ensemble effect modifies the maximum values of all the properties studied in this work. For example, comparing the values of the velocity amplitude for the case N4 with the case N1 in the total N1 result area, for $\theta =0°$, the velocity amplitude experience at certain points a maximum increment and reduction of 68% and 99%, respectively, for $T=6\text{s}$, and 76% and 99%$T=12\text{s}$. Therefore, even for cylinders $25>d/L>1$ the system cannot be studied as individual cylinders.

For both N1 and N4 cases, bottom velocities, mean water level and radiation stresses experienced diffraction effects before the cylinders, whereas the diffraction effects on mass transport appears more significantly after the incident waves meet the structures. The effect of the structures on the amplitude of the bottom velocity and the mean water level showed the formation of a reflective wave pattern in front of the cylinders. This wave modifies the mean water level of the incident waves with a periodicity of $L/2$. Behind the structures, results for the diffracted wave confirm the interactions between the scattered and the incident waves. Spatial variations that depended on the wave propagation angle were observed for the N4 case, which means that the relative distances and positions of the cylinders influence in the diffraction pattern. For $T=12\text{s}$, $(D/L\le 2)$, the diffraction effects due to the presence of four cylinders are significant and greater than the results of one cylinder, especially for bottom velocities and radiations stresses.

Concerning the radiation stress tensor, an oscillating pattern of radial and azimuthal radiation stresses, for one cylinder and four cylinders, respectively, manifests on the up-wave side. Down-wave, the pattern also varies spatially but strongly depends on the incident wave direction. Special attention should be given to the shear stress component $S_{xy}$. While it remains constant for progressive monochromatic waves on a mild constant sloped bottom (or constant depth), in the present case it undergoes significant spatial variations after the introduction of the cylinders.

Important spatial variations in bottom velocities, mass transport, mean water level and radiation stresses due to diffraction effects of all the cylinders for the N4 case have been presented. Bottom velocities are important for sediment and morphodynamic processes around the cylinders; mass transport is relevant for oil dispersion and debris transport; variations on the mean water level can affect the calculations of loads on the cylinders; and, radiation stresses affect the momentum flux through the array, which will propagate away from the array towards the coast and ultimately affect nearshore processes. If the four cylinders array is considered as the basic unit of offshore monopile turbines, computing those quantities and analyzing the effect of the completed array was proved to be necessary. The results of this paper also indicate that further investigations with larger monopile/cylinder arrays should be investigated for the environmental impact assessment on wave climate due to large wind farms.

ACKNOWLEDGEMENTS

This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001. The authors acknowledge and are thankful for the support of the Laboratory of Ocean Technology (LabOceano) of the Federal University of Rio de Janeiro for using the WAMIT®. The authors also thank Dr. Marcos Donato A. S. Ferreira for the interesting discussions and orientation about the use of WAMIT®.

REFERENCES

• Abul-Azm, A. G., & Williams, A. N. (1989). Approximation of second-order diffraction loads on arrays of vertical circular cylinders. Journal of Fluids and Structures, 3(1), 17-36. http://dx.doi.org/10.1016/S0889-9746(89)80010-6
  » http://dx.doi.org/10.1016/S0889-9746(89)80010-6
• Baidya Roy, S., Pacala, S. W., & Walko, R. L. (2004). Can large wind farms affect local meteorology? Journal of Geophysical Research, D, Atmospheres, 109(19), 1-6. http://dx.doi.org/10.1029/2004JD004763
  » http://dx.doi.org/10.1029/2004JD004763
• Bihs, H., Chella, M. A., Kamath, A., & Arntsen, Ø. A. (2017). Numerical investigation of focused waves and their interaction with a vertical cylinder using REEF3D. Journal of Offshore Mechanics and Arctic Engineering, 139(4), 041101. http://dx.doi.org/10.1115/1.4036206
  » http://dx.doi.org/10.1115/1.4036206
• Brasseur, S., Kirkwood, R., & Aarts, G. (2018). Seal monitoring and evaluation for the Gemini offshore windfarm: Tconstruction - 2015 report Wageningen: Wageningen University. Report-C004/18. Https://doi.org/10.18174/431831.
• Breton, S. P., & Moe, G. (2009). Status, plans and technologies for offshore wind turbines in Europe and North America. Renewable Energy, 34(3), 646-654. http://dx.doi.org/10.1016/j.renene.2008.05.040
  » http://dx.doi.org/10.1016/j.renene.2008.05.040
• Cazenave, P. W., Torres, R., & Allen, J. I. (2016). Unstructured grid modelling of offshore wind farm impacts on seasonally stratified shelf seas. Progress in Oceanography, 145(2016), 25-41. http://dx.doi.org/10.1016/j.pocean.2016.04.004
  » http://dx.doi.org/10.1016/j.pocean.2016.04.004
• Chau, F. P., & Taylor, R. E. (1992). Second-order wave diffraction by a vertical cylinder. Journal of Fluid Mechanics, 240(1), 571-599. http://dx.doi.org/10.1017/S0022112092000211
  » http://dx.doi.org/10.1017/S0022112092000211
• Christensen, E. D., Kristensen, S. E., & Deigaard, R. (2014). Impact of an offshore wind farm on wave conditions and shoreline development. In Proceedings of the 34th Coastal Engineering Conference (pp. 1-13). Seoul: ICCE. http://dx.doi.org/10.9753/icce.v34.sediment.87
  » http://dx.doi.org/10.9753/icce.v34.sediment.87
• Dean, R. G., & Darlymple, R. A. (1991). Water wave mechanics for engineers and scientists (Vol. 2). Singapore: World Scientific Publishing Company. https://doi.org/10.1142/1232
  » https://doi.org/10.1142/1232
• Ghalayini, S. A., & Williams, A. N. (1991). Nonlinear wave forces on vertical cylinder arrays. Journal of Fluids and Structures, 5(1), 1-32. http://dx.doi.org/10.1016/0889-9746(91)80009-3
  » http://dx.doi.org/10.1016/0889-9746(91)80009-3
• Global Wind Energy Council – GWEC. (2019). Global wind report 2018 Brussels. Retrieved in 2019, September 23, from www.gwec.net
• Hasager, C., Vincent, P., Badger, J., Badger, M., Di Bella, A., Peña, A., Husson, R., & Volker, P. (2015). Using satellite SAR to characterize the wind flow around offshore wind farms. Energies, 8(6), 5413-5439. http://dx.doi.org/10.3390/en8065413
  » http://dx.doi.org/10.3390/en8065413
• Havelock, T. H. (1940). The pressure of water waves upon a fixed obstacle. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 175(963), 409-421. http://dx.doi.org/10.1098/rspa.1940.0066
  » http://dx.doi.org/10.1098/rspa.1940.0066
• Huang, J. B. (2004). Nonlinear free surface action with an array of vertical cylinders. Acta Mechanica Sinica, 20(3), 247-262. http://dx.doi.org/10.1007/BF02486717
  » http://dx.doi.org/10.1007/BF02486717
• Kagemoto, H., & Yue, D. K. P. (1986). Interactions among multiple three-dimensional bodies in water waves: an exact algebraic method. Journal of Fluid Mechanics, 166(1), 189. http://dx.doi.org/10.1017/S0022112086000101
  » http://dx.doi.org/10.1017/S0022112086000101
• Kagemoto, H., Murai, M., Saito, M., Molin, B., & Malenica, Š. (2002). Experimental and theoretical analysis of the wave decay along a long array of vertical cylinders. Journal of Fluid Mechanics, 456, 113-135. http://dx.doi.org/10.1017/S0022112001007480
  » http://dx.doi.org/10.1017/S0022112001007480
• Kagemoto, H., Murai, M. & Fujii, T. (2014). Second-order resonance among an array of two rows of vertical circular cylinders. Applied Ocean Research, 47, 192–198. http://dx.doi.org/10.1016/j.apor.2014.05.002
  » http://dx.doi.org/10.1016/j.apor.2014.05.002
• Kamath, A., Alagan Chella, H., Bihs, H., & Arntsen, Ø. A. (2016). Breaking wave interaction with a vertical cylinder and the effect of breaker location. Ocean Engineering, 128, 105-115. http://dx.doi.org/10.1016/j.oceaneng.2016.10.025
  » http://dx.doi.org/10.1016/j.oceaneng.2016.10.025
• Kamra, M. M., Al Salami, J., Sueyoshi, M., & Hu, C. (2019). Experimental study of the interaction of dambreak with a vertical cylinder. Journal of Fluids and Structures, 86, 185-199. http://dx.doi.org/10.1016/j.jfluidstructs.2019.01.015
  » http://dx.doi.org/10.1016/j.jfluidstructs.2019.01.015
• Kareem, A., Williams, A. N., & Hsieh, C. C. (1994). Diffraction of nonlinear random waves by a vertical cylinder in deep water. Ocean Engineering, 21(2), 129-154. http://dx.doi.org/10.1016/0029-8018(94)90035-3
  » http://dx.doi.org/10.1016/0029-8018(94)90035-3
• Kim, M.-H. (1988). The complete second-order diffraction and radiation solutions for a vertically axisymmetric body (Thesis). Department of Ocean Engineering, Massachusetts Institute of Technology, Massachusetts. Retrieved from https://dspace.mit.edu/handle/1721.1/35346
  » https://dspace.mit.edu/handle/1721.1/35346
• Kim, M.-H., & Chen, W. (1994). Slender-body approximation for slowly-varying wave loads in multi-directional waves. Applied Ocean Research, 16(3), 141-163. http://dx.doi.org/10.1016/0141-1187(94)90025-6
  » http://dx.doi.org/10.1016/0141-1187(94)90025-6
• Kim, M.-H., & Yue, D. K. P. (1989). The complete second-order diffraction solution for an axisymmetric body Part 1. Monochromatic incident waves. Journal of Fluid Mechanics, 200, 235-264. http://dx.doi.org/10.1017/S0022112089000649
  » http://dx.doi.org/10.1017/S0022112089000649
• Kim, M.-H., & Yue, D. K. P. (1990). The complete second-order diffraction solution for an axisymmetric body part 2. Bichromatic incident waves and body motions. Journal of Fluid Mechanics, 211, 557-593. http://dx.doi.org/10.1017/S0022112090001690
  » http://dx.doi.org/10.1017/S0022112090001690
• Korsmeyer, F. T., Lee, C. H., Newman, J. N., & Sclavounos, P. D. (1988). The analysis of wave interactions with tension leg platforms. In Proceedings of the Conference on Ocean Offshore & Arctic Engineering New York: ASME.
• Kriebel, D. L. (1990). Nonlinear wave interaction with a vertical circular cylinder. Part I: diffraction theory. Ocean Engineering, 17(4), 345-377. http://dx.doi.org/10.1016/0029-8018(90)90029-6
  » http://dx.doi.org/10.1016/0029-8018(90)90029-6
• Kriebel, D. L. (1992). Nonlinear wave interaction with a vertical circular cylinder. Part II: wave run-up. Ocean Engineering, 19(1), 75-99. http://dx.doi.org/10.1016/0029-8018(92)90048-9
  » http://dx.doi.org/10.1016/0029-8018(92)90048-9
• Linton, C. M., & Evans, D. V. (1990). The interaction of waves with arrays of vertical circular cylinders. Journal of Fluid Mechanics, 215(1), 549. http://dx.doi.org/10.1017/S0022112090002750
  » http://dx.doi.org/10.1017/S0022112090002750
• Longuet-Higgins, M. S. (1969). On the transport of mass by time-varying ocean currents. Deep-Sea Research and Oceanographic Abstracts, 16(5), 431-447. http://dx.doi.org/10.1016/0011-7471(69)90031-X
  » http://dx.doi.org/10.1016/0011-7471(69)90031-X
• Longuet-Higgins, M. S., & Stewart, R. W. (1962). Radiation stress and mass transport in gravity waves, with application to ‘surf beats’. Journal of Fluid Mechanics, 13(4), 481-504. http://dx.doi.org/10.1017/S0022112062000877
  » http://dx.doi.org/10.1017/S0022112062000877
• Longuet-Higgins, M. S., & Stewart, R. W. (1964). Radiation stresses in water waves; a physical discussion, with applications. Deep-Sea Research, 11(4), 529-562. https://doi.org/10.1016/0011-7471(64)90001-4
  » https://doi.org/10.1016/0011-7471(64)90001-4
• MacCamy, R. C., & Fuchs, R. A. (1954). Wave forces on piles: a diffraction theory Washington: U.S. Beach Erosion Board.
• McIver, P. (2002). Wave interaction with arrays of structures. Applied Ocean Research, 24(3), 121-126. http://dx.doi.org/10.1016/S0141-1187(02)00034-2
  » http://dx.doi.org/10.1016/S0141-1187(02)00034-2
• Mohseni, M., Esperanca, P. T., & Sphaier, S. H. (2018). Numerical study of wave run-up on a fixed and vertical surface-piercing cylinder subjected to regular, non-breaking waves using OpenFOAM. Applied Ocean Research, 79, 228-252. http://dx.doi.org/10.1016/j.apor.2018.08.003
  » http://dx.doi.org/10.1016/j.apor.2018.08.003
• Molin, B. (1979). Second-order diffraction loads upon three-dimensional bodies. Applied Ocean Research, 1(4), 197-202. http://dx.doi.org/10.1016/0141-1187(79)90027-0
  » http://dx.doi.org/10.1016/0141-1187(79)90027-0
• Moubayed, W. I., & Williams, A. N. (1995). Second-Order hydrodynamic interactions in an array of vertical cylinders in bichromatic waves. Journal of Fluids and Structures, 9(1), 61-98. http://dx.doi.org/10.1006/jfls.1995.1004
  » http://dx.doi.org/10.1006/jfls.1995.1004
• Newman, J. N. (2014). Cloaking a circular cylinder in water waves. European Journal of Mechanics - B/Fluids, 47, 145-150. http://dx.doi.org/10.1016/j.euromechflu.2013.11.005
  » http://dx.doi.org/10.1016/j.euromechflu.2013.11.005
• Ohl, C. O. G., Taylor, P. H., Taylor, R. E., & Borthwick, A. G. L. (2001b). Water wave diffraction by a cylinder array. Part 2: irregular waves. Journal of Fluid Mechanics, 442(2001), 33-66. http://dx.doi.org/10.1017/S0022112001004943
  » http://dx.doi.org/10.1017/S0022112001004943
• Ohl, C. O. G., Taylor, R. E., Taylor, P. H., & Borthwick, A. G. L. (2001a). Water wave diffraction by a cylinder array. Part 1: regular waves. Journal of Fluid Mechanics, 442(2001), 1-32. http://dx.doi.org/10.1017/S0022112001004931
  » http://dx.doi.org/10.1017/S0022112001004931
• Ørsted. (2017). Walney extension offshore wind farm London. Retrieved in 2019, September 23, from https://walneyextension.co.uk/-/media/WWW/Docs/Corp/UK/Walney-extension/180822_Walney-Extension-Project-Summary-V4.ashx?la=en&hash=4F8D0C0F6EE86D9300B36D2DEFB3462DA4A9C419
  » https://walneyextension.co.uk/-/media/WWW/Docs/Corp/UK/Walney-extension/180822_Walney-Extension-Project-Summary-V4.ashx?la=en&hash=4F8D0C0F6EE86D9300B36D2DEFB3462DA4A9C419
• Read, R., Bingham, H., & Newman, J. (2018). Measurements of water-wave cloaking by an array of circular cylinders. International Journal of Offshore and Polar Engineering, 28(2), 128-134. http://dx.doi.org/10.17736/ijope.2018.jc714
  » http://dx.doi.org/10.17736/ijope.2018.jc714
• Segtnan, O. H., & Christakos, K. (2015). Effect of offshore wind farm design on the vertical motion of the ocean. Energy Procedia, 80, 213-222. http://dx.doi.org/10.1016/j.egypro.2015.11.424
  » http://dx.doi.org/10.1016/j.egypro.2015.11.424
• Sharma, J. N., & Dean, R. G. (1981). Second-order directional seas and associated wave forces. Society of Petroleum Engineers Journal, 21(1), 129-140. http://dx.doi.org/10.2118/8584-PA
  » http://dx.doi.org/10.2118/8584-PA
• Spring, B. H., & Monkmeyer, P. L. (1974). Interaction of plane waves with vertical cylinders. In Proceedings of the 14th Coastal Engineering Conference (pp. 1828-1847). Copenhagen: ICCE. https://doi.org/10.9753/icce.v14.107
  » https://doi.org/10.9753/icce.v14.107
• Steward, D. R. (2018). Wave resonance and dissipation in collections of partially reflecting vertical cylinders. Journal of Waterway, Port, Coastal, and Ocean Engineering, 144(4), 1-16. http://dx.doi.org/10.1061/(ASCE)WW.1943-5460.0000443
  » http://dx.doi.org/10.1061/(ASCE)WW.1943-5460.0000443
• Stokes, G. G. (1880). On the theory of oscillatory waves (Mathematical and Physical Papers, Vol. 1, pp. 197-229). Cambridge: Cambridge University Press. https://doi.org/10.1017/CBO9780511702242.013
  » https://doi.org/10.1017/CBO9780511702242.013
• Sumer, B. M., & Fredsøe, J. (1997). Hydrodynamics around cylindrical structures (Vol. 12). Hackensack: World Scientific. http://dx.doi.org/10.1142/3316
  » http://dx.doi.org/10.1142/3316
• Taylor, R. E., & Huang, J. B. (1997). Second-order wave-diffraction by an axisymmetric body in monochromatic waves. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 453(1962), 1515-1541. http://dx.doi.org/10.1098/rspa.1997.0081
  » http://dx.doi.org/10.1098/rspa.1997.0081
• Tucker, V. A. (1996). A mathematical model of bird collisions with wind turbine rotors. Journal of Solar Energy Engineering, 118(4), 253-262. http://dx.doi.org/10.1115/1.2871788
  » http://dx.doi.org/10.1115/1.2871788
• Van Den Bremer, T. S., & Breivik, Ø. (2018). Stokes drift. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 376(2111), 20170104. http://dx.doi.org/10.1098/rsta.2017.0104
  » http://dx.doi.org/10.1098/rsta.2017.0104
• Vanhellemont, Q., & Ruddick, K. (2014). Turbid wakes associated with offshore wind turbines observed with Landsat 8. Remote Sensing of Environment, 145, 105-115. http://dx.doi.org/10.1016/j.rse.2014.01.009
  » http://dx.doi.org/10.1016/j.rse.2014.01.009
• Vepa, R. (2013). Dynamic modeling, simulation and control of energy generation (Vol. 20). London: Springer. http://dx.doi.org/10.1007/978-1-4471-5400-6
  » http://dx.doi.org/10.1007/978-1-4471-5400-6
• Walker, D. A. G., & Taylor, R. E. (2005). Wave diffraction from linear arrays of cylinders. Ocean Engineering, 32(17-18), 2053-2078. http://dx.doi.org/10.1016/j.oceaneng.2005.04.002
  » http://dx.doi.org/10.1016/j.oceaneng.2005.04.002
• Wang, C. Z., & Wu, G. X. (2007). Time domain analysis of second-order wave diffraction by an array of vertical cylinders. Journal of Fluids and Structures, 23(4), 605-631. http://dx.doi.org/10.1016/j.jfluidstructs.2006.10.008
  » http://dx.doi.org/10.1016/j.jfluidstructs.2006.10.008
• Wei, K., Arwade, S. R., & Myers, A. T. (2014). Incremental wind-wave analysis of the structural capacity of offshore wind turbine support structures under extreme loading. Engineering Structures, 79, 58-69. http://dx.doi.org/10.1016/j.engstruct.2014.08.010
  » http://dx.doi.org/10.1016/j.engstruct.2014.08.010

Publication Dates

• Publication in this collection
  27 Apr 2020
• Date of issue
  2020

History

• Received
  23 Sept 2019
• Reviewed
  24 Feb 2020
• Accepted
  27 Feb 2020