Optimal policies for activated sludge treatment systems with multi effluent stream generation

OPTIMAL POLICIES FOR ACTIVATED SLUDGE TREATMENT SYSTEMS WITH MULTI EFFLUENT STREAM GENERATION

R.Gouveia and J.M.Pinto^*

Department of Chemical Engineering, University of São Paulo, São Paulo - SP, Brazil

05508-900, Phone [phone], Fax [phone],

E-mail [e-mail]

(Received: November 19, 1999 ; Accepted: May 18, 2000)

Abstract - Most industrial processes generate liquid waste, which requires treatment prior to disposal. These processes are divided into sectors that generate effluents with time dependent characteristics. Each sector sends the effluent to wastewater treatment plants through pumping-stations. In general, activated sludge is the most suitable treatment and consists of equalization, aeration and settling tanks. During the treatment, there is an increase in the mass of microorganisms, which needs to be removed. Sludge removal represents the major operating costs for wastewater treatment plants. The objective of this work is to propose an optimization model to minimize sludge generation using a superstructure in which the streams from pumping-stations can be sent to the equalization tank. In addition, the aeration tank is divided into cells that can be fed in series and parallel. The model relies on mass balances, kinetic equations, and the resulting Nonlinear Programming problem generates the best operational strategy for the system feed streams with a high substrate removal. Reductions of up to 30 % can be achieved with the proposed strategy maintened BOD efficiency removal upper than 98 %.

Keywords: wastewater treatment, nonlinear optimization, sludge discharge minimization.

INTRODUCTION

The wastewater generation is common to every industry, such as textiles, tanneries, chemicals, food processing and paper as a result of the production process. In the majority of cases, the most suitable treatment to reduce the organic charges in wastewater is the activated sludge process (Nemerow and Dasgupta, 1991). This process consists of an aeration tank and a settling tank (Jenkins et al., 1993), as seen in Figure 1.

The aeration tank receives the effluent stream and treats it with an activated mass of microorganisms maintained in suspension and capable of stabilizing the substrate aerobically (Tchobanoglous and Burton, 1991). The stabilization is done by removing soluble and insoluble organic compounds from the effluent stream and converting this material into a flocculent microbial suspension, which can be separated in a settling tank (Eckenfelder Jr., 1989).

In many industrial facilities, wastewater is generated with toxic compounds to the activated sludge process as well as variable flowrates and characteristics. In these situations, the wastewater system requires pre-treatment devices to make treatment possible.

Pre-treatment devices in general rely on chemical or physical treatments to remove toxic compounds, solids or to reduce the organic load and on equalization tanks to homogenize the inflow wastewater characteristics. Other devices generally found in activated sludge treatment systems is pumping station, whose function is not to treat the wastewater but to send the wastewater from lower to higher locations. These units are designed based on peak flowrates and consequently have considerable volumes.

During the activated sludge treatment there is an increase in the mass of activated microorganisms (sludge), which needs to be removed. The removal of sludge (dewatering, disposal, etc.) represents generally major investment and operating costs for wastewater treatment plants (Nemerow and Dasgupta, 1991).

A straightforward way of reducing sludge waste is to manipulate the Solids Retention Time (SRT). When SRT increases, sludge production decreases (Lee and Welander, 1996). In order to increase SRT one must increase the total mass of microorganisms, which is conventionally achieved in two ways: either raising microorganisms concentration or increasing the volume of the aeration tank. However there are limitations in the increase of microorganism concentration (e.g. operational problems, oxygen demand). On the other hand, changes in the tank volume require a complete retrofit of the system.

Another form of reducing sludge disposal involves the addition of an aerobic or anaerobic digester (generally used in large plants). Digester systems that reduce sludge disposal volume are mostly applied in municipal wastewater treatment plants (Tang et al., 1987a; Tang et al., 1987b; Tang and Ellis, 1991; Tang and Ellis, 1994) and require significant capital investment. Alternative forms also include the usage of cultured microorganisms in the aeration tank (Lee and Welander, 1996), instigation of the partial lisy of microorganisms by heating the sludge recycle (Low and Chase, 1999); both must be very carefully operated in order to control microorganism population. All these forms of sludge reduction are out of the scope of this work.

Gouveia and Pinto (1998) developed an optimization model for the optimal selection of the aeration tank configuration for sludge discharge minimization by assuming that the aeration tanks are divided in cells and operated at steady state. A dynamic model that accounts for daily variations in flowrate and concentrations of the effluent stream was developed with the addition of an equalization tank (Gouveia and Pinto, 1999).

This work proposes an optimization model for minimizing the sludge discharge in an activated sludge treatment plant based on the variables usually measured in this system. Moreover, the treatment system consists of pumping stations, an equalization tank, aeration tanks subdivided into a sequence of cells, and settling tank. By adequately manipulating the feed streams in pumping stations, equalization tank and aeration tank the sludge growth rate is minimized. The model is composed of mass balances (global, substrate, microorganism and oxygen) for the pumping stations, equalization tank, for the cells of the aeration tank as well as for the settling tank. Due to the nonlinear nature of the reaction kinetics, the resulting model is a nonlinear programming (NLP) problem, which is solved by the reduced gradient method.

PROBLEM DESCRIPTION

Consider an industrial process with several production lines, each generating effluent streams at different flowrates and compositions. A simple strategy is to send these streams to an equalization tank as these are generated. However, this may cause an overload in the treatment plant. An alternative approach is to make use of pumping stations, which have significant storage space. In this way, the effluent streams may be appropriately handled by synchronizing pumping operations. Therefore, the resulting effluent stream that enters the activated sludge plant can be more efficiently treated.

Industrial wastewater plants in general have an equalization tank with capacity to homogenize the composition and flowrate of the effluent generated in the industrial process. This equalization tank is designed so to accept certain composition variations in the outlet stream (or feed stream to the aeration tank). Peaks in the organic load cause an increase in sludge discharge; nevertheless, decreases in the organic load in general do not compensate for these peaks thus causing overload in the treatment system (Gouveia and Pinto, 1998; Gouveia and Pinto, 1999).

In the aeration tank, there is a sequence of cells, which are usually operated in series. The feed stream enters the first cell as well as a sludge recycle stream. The outlet stream of the last cell enters a settling tank, where is separated into a stream that contains the treated effluent and a sludge stream; a portion of the latter is disposed and the remaining is recycled to the aeration tank.

OPTIMIZATION MODEL

In this Section, we propose a mathematical programming model the minimization of the sludge growth rate of the complete system to obtain the following operating variables:

1) flowrate and compositions of the outlet streams from pumping stations;

2) flowrate and composition of the equalization tank outlet streams;

3) flowrate and compositions of the wastewater feed and liquor recycle in each cell of the aeration tank.

In order to develop the optimization model we first define the superstructure seen in Figure 2. There are m pumping stations (ps) that receive effluent (pe) from different parts of the plant at different flowrates and loads. This mixture is sent to an equalization tank (te) that controls the resulting flowrate (e) and further distributes it along the aeration tank divided into n cells arranged in a generic (series and/or parallel) configuration. These cells also receive the recycle stream (rec). The two streams that leave the system are the treated effluent (sdec) and the sludge waste (des).

The model relies on the following assumptions:

A1. It is possible to control the exit flowrate of pumping stations

A2. The cells (subdivisions of the aeration tank) are identical CSTR reactors. This is a reasonable assumption due to the high degree of mixing provided by the aeration system.

A3. Each cell has the same volume and air supply.

A4. The absorption of oxygen does not aggregate mass to the system.

A5. The concentration of microorganisms in the tank can be inferred by the measurement of the Mixed-Liquor Volatile Suspended Solids (MLVSS). This measure is the simplest way to obtain the amount of microorganisms in the aeration tank (Von Sperling, 1996).

A6. Density is independent of MLVSS changes.

A7. The settling tank receives effluent and sludge from cell "n" and doubles MLVSS concentration in the recycle stream.

A8. Substrate concentration in the settling tank is not changed.

A9. Sludge waste has the same characteristics of recycle sludge.

A10. The nutrients are in sufficient and necessary concentration in effluent.

A11. The limiting substrate is biological oxygen demand (BOD).

A12. The system is operated under isothermal conditions.

A13. Chemical or biological reactions do not take place in pumping stations, equalization tank and settling tank.

A14. Changes in flowrates and concentrations occur in steps.

With the above assumptions, we develop mass balances around the pumping stations, equalization tank, cells and the settling tank.

Model equations

The mass balances are developed for the pumping stations, the equalization tank, cells of the aeration tank and the settling tank. The variables used in this model are seen in Figure 2. Moreover, balances in transient mode are developed on a volumetric basis as a consequence of assumption A6 and represent the differential equations discretized in intervals of equal length.

Pumping Station j

We use generic mass balances in the j^th pumping station. Only global and substrate mass balances are considered, since we do not consider the existence of microorganisms in pumping station neither consumption / transfer of oxygen.

Global mass balance:

(1-j,t)

Substrate mass balance:

(2-j,t)

Equalization Tank

Again, only global and substrate mass balances are considered, since we do not consider the existence of microorganisms in pumping station neither consumption / transfer of oxygen in the equalization tank.

Global mass balance:

(3-t)

Substrate mass balance:

(4-t)

Aeration Tank - Cell k

We use generic mass balances in the k^th cell (ASCE, 1992; Horváth, 1984; Jordão and Pessôa, 1975; Springer, 1993). The first cell does not receive effluent from the previous cell, therefore for cell k=1 terms with k-1 (= 0) must be deleted. It is important to note that the aeration tank operates in overflow mode.

Global mass balance:

(5-k,t)

Microorganism or MLVSS mass balance:

(6-k,t)

The rate expressions are given in (6-k,t) by a growth term that follows a Monod-like kinetics and a decay term.

Substrate mass balance:

(7-k,t)

Oxygen mass balance:

(8-k,t)

where:

(9-k,t)

(10)

(11-k,t)

(12-k,t)

Equations (9-k,t) and (10) are given for a ceramic diffuser (Norton, 1979). These equations could be replaced by any others that would represent the efficiency of air diffusers. Equation (11-k,t) represents the saturated oxygen in the wastewater and (12-k,t) denotes the concentration of oxygen in the air that leaves the tank (Eckenfelder Jr., 1989).

Settling Tank

The settling tank also operates in overflow mode and therefore there is no accumulation term in the global mass balance, equation (13-t). We do not consider consumption and oxygen transfer in the settling tank.

Global mass balance:

(13-t)

Microorganism or MLVSS mass balance:

(14-t)

Substrate mass balance:

(15-t)

Additional Mass Balances

The model requires extra additional mass balances for the total effluent and recycle streams, as in (16-t) and (17-t):

(16-t)

(17-t)

The sludge discarded is represented by the sludge waste and the involuntary discharge is represented by the sludge present in treated effluent. This can be written as:

(18)

The efficiency of substrate removal can be represented by:

(19-t)

Model Structure

The model for minimizing sludge discharge can be written as:

Minimize (18)

subject to:

(1-j,t) - (2-j,t)

pumping station

(3-t) - (4-t)

equalization tank

(5-k,t) - (9-k,t)

aeration tank

(10) - (11-k,t) - (12-k,t)

aeration tank

(13-t) - (15-t)

settling tank

(16-t)

total effluent balance

(17-t)

total recycle balance

(19-t)

efficiency requirement

The Non-Linear Programming (NLP) model is developed with (2^.m^.p +7^.m^.n+9^.m+1) equations and (3^.m^.p + 9^.n^.m+13^.m+ 1) continuous non-negative variables. It is important to note that the two major sources of non-linearity are the reaction kinetics and the component mass balances. From assumptions A7 and A8, we have and S_rec,t = S_des,t = ; thus, there are (2^.n + p + 1)^.m degrees of freedom, where n is the number of cells, m is the number of pumping stations and p corresponds to the number of time intervals.

The n cells in the aeration tank have the same volume that is calculated by the following equation:

(20-k)

The overall air flowrate is also equally divided among the n cells, and thus represented by equation (21-k):

(21-k)

Values of MLVSS are bounded to (k = 1,....,n-1), since higher values may cause operating problems (Eckenfelder Jr, 1989). The cell that feeds the settling tank (cell n) has an upper bound of , which is the concentration of microorganisms usually found in water treatment systems.

By maintaining the oxygen concentration above 2.0 mg/l in the outlet stream of each cell, we avoid operational problems in the settling tank as well as odor emanation.

The legislation establishes that at least 80% of the organic load in the form of BOD is removed. As a safety measure, we established a lower bound of 85% on the removal.

RESULTS

In order to test the model, we propose a wastewater treatment plant with the typical values shown in table 1 (units for the parameters given in Sec. 3.1) and figure 3. Note that a one-day horizon was applied with one-hour time intervals and the minimum efficiency of the system at every time is 85%.

The modeling system GAMS (Brooke et al., 1992) was used to implement the model and the solution is obtained with the nonlinear programming code CONOPT based on the Generalized Reduced Gradient method (Drud, 1994). The optimization model was solved for four cells in the aeration tank and the results for the main variables are shown in figures 4 - ⁶.

In figure 4, the results for the feed flowrates of each of the pumping stations are shown, while ^{figure 5} shows the inlet flowrates from the equalization tank and from recycle for each of the cells of the aeration tank. Finally, in figure 6, the overall efficiency of the system is shown along the horizon.

As seen in ^{figure 5}, feeding of the cells occurs in a similar way of that observed in steady state mode (Gouveia and Pinto, 1998). The recycle stream feeds mostly the first cell in the aeration tank, while the effluent stream is subdivided among the cells, being the larger portions sent to cells 3 and 4.

Figure 6 shows that at every time the substrate removal efficiency remains high, (in the 98.5 – 99.7 range). It is important to note that the lower bound was defined as 85% as mentioned in Section 3.2.

The minimization in sludge discharge when the pumping stations are included in the equalization system was compared with several models developed by Gouveia and Pinto (1998, 1999) for different cases, as follows:

Case 1 - Results obtained from the present model.

Case 2 - Non-stationary model and aeration tank with four cells, with time dependent feed flowrate and substrate concentration along the horizon (Gouveia and Pinto, 1999).

Case 3 - Stationary model and aeration tank with four cells (Gouveia and Pinto, 1998) with constant feed flowrate Q_e = 1200 m³/d and substrate concentration of 1000 mg/l along the horizon. This case represents sludge minimization for the steady state case.

Case 4 - Stationary model and aeration tank with one cell (Gouveia and Pinto 1998) with constant feed flowrate Q_e = 1200 m³/d and substrate concentration of 1000 mg/l. This case corresponds to the usual way of operating such activated sludge treatment systems.

Table 3 shows the number of variables, equations and non-zero elements of the cases shown. Also shown are the computational times for obtaining the optimal solution in a Pentium 200 MMX processor.

CONCLUSIONS

The minimization in sludge discharge when the pumping stations are considered as pre equalizations systems provide a 39% reduction with respect to Case 2, 48% with respect to Case 3 and 58% to Case 4, while still maintaining a high efficiency. This shows the importance of equalization systems in industrial wastewater systems and the advantages in modeling the entire system.

ACKNOWLEDGEMENTS

The authors acknowledge support from FAPESP – Fundação de Amparo à Pesquisa do Estado de São Paulo - under grant 99/05575-2.

NOMECLATURE

Indices

k cell in aeration tank(1,....,n) j pumping station (1,....,m) t time interval (0,...,p)

Parameters

a ratio of oxygen transfer rate in effluent and oxygen transfer rate in clean water (dimensionless). b ratio of oxygen saturated concentration in effluent and oxygen saturated concentration in clean water (dimensionless). Dt time interval (h). m_m maximum specific growth rate (d^-1). a’ oxygen consumption to remove the substrate (dimensionless). b’ oxygen consumption to endogenous respiration of microorganisms (d^-1). CS oxygen saturation concentration of clean water (mg/l). EFF^L lower bound on the efficiency of substrate removal (%). H effective height of effluent in cells (m). k_max maximum rate of substrate utilization per unit mass of microorganisms (d^-1). k_d endogenous decay coefficient (d^-1). K_s half-velocity constant (mg/l). P atmospheric pressure (m H₂O). Q_air total air flowrate in the aeration tank (m³/min). air flowrate in cell k of the aeration tank (m³/min). inflow of effluent to pumping station j at time t (m³/d). biochemical oxygen demand of effluent of inflow effluent in pumping station j at time t (mg/l). V volume of the aeration tank (m³). volume of pumping station j (m³). volume of cell k (m³). maximum volume storage from equalization tank (m³).

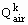
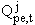
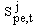
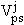
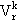
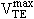
Variables

oxygen concentration in half-depth of cell k at time t (mg/l). CO_e,t oxygen concentration of inlet effluent to aeration tank at time t (mg/l). CO_rec,t oxygen concentration of recycle stream at time t (mg/l). oxygen concentration in cell k at time t (mg/l). DL^T total sludge discharge within the horizon (kg/d). E₀ efficiency of oxygen transfer to clean water (%). efficiency of oxygen transfer to effluent in cell k at time t (%). percent oxygen concentration in the air that leaves cell k of the aeration tank (%). Q_des,t outflow of sludge waste (m³/d). Q_e,t outflow of effluent from equalization tank at time t (m³/d). inflow of effluent in cell k at time t (m³/d). outflow of effluent to pumping station j at time t (m³/d). Q_rec,t total flow of sludge recycle at time t (m³/d). inflow of sludge recycle stream in cell k at time t (m³/d). outflow of cell k at time t (m³/d). Q_sdec,t outflow of treated effluent at time t (m³/d). S_des,t biochemical oxygen demand of sludge waste at time t (mg/l). S_e,t biochemical oxygen demand of equalization tank outlet stream at time t (mg/l). biochemical oxygen demand of outflow effluent in pumping station j at time t (mg/l). S_rec,t biochemical oxygen demand of recycle stream at time t (mg/l). biochemical oxygen demand in cell k at time t (mg/l). S_sdec,t biochemical oxygen demand of treated effluent at time t (mg/l). volume of effluent in pumping station j at time t (m³). V_TE,t volume of effluent in equalization tank at time t (m³). X_des,t MLVSS of sludge waste at time t (mg/l). X_e,t MLVSS of inlet stream to the aeration tank at time t (mg/l). X_rec,t MLVSS of recycle stream at time t (mg/l). MLVSS of cell k at time t (mg/l). X_sdec,t MLVSS of treated effluent at time t (mg/l).

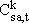
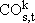
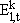
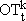
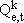
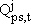
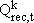
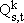
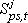
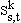
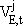
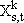
REFERENCES

Norton Aeration/Filtration Systems, Norton Company – Industrial Ceramics Division – Worcester (1979).

• ASCE, Design of Municipal Wastewater Plants, Vol. 1 , Joint task force of the Water Environment Federation and the American Society of Civil Engineers, 2^nd ed., Book Press, Battleboro (1992).
• Brooke, A.; Kendrick, D. and Meeraus, A.; GAMS - A users guide (release 2.25), The Scientific Press, San Francisco (1992).
• Drud, A.S.; CONOPT - A Large-Scale GRG Code, ORSA Journal on Computing, 6, No. 2, p. 207 - 216, (1994).
• Eckenfelder Jr, W.W.; Industrial water pollution control, McGraw-Hill International Editions, New York (1989).
• Gouveia, R. and Pinto, J. M.; Sludge Minimization Discharge in Activated Sludge Treatment Plants, Anais do IX Congresso Latinoiberoamericano de Investigación Operativa, Buenos Aires (1998).
• Gouveia, R. and Pinto, J. M.; Optimal Operating Policies in Activated Sludge Treatment Plants, Computers & Chemical Engineering, 23 (suppl.), p. S853 S856 (1999).
• Horváth, I.; Modeling in Technology of Wastewater Treatment, Pergamon Press, Oxford (1984).
• Jenkins, D.; Richard, M.G. and Daigger, G.T.; manual on the Causes and Control of Activated Sludge Bulking and Foaming, Lewis Publishers (1993).
• Jordão, E.P. and Pessôa, C.A.; Tratamento de esgotos domésticos. vol I Concepções clássicas de tratamento, Cetesb, São Paulo (1975).
• Lee, N.M. and Welander, T.; Reducing Sludge Production in Aerobic Wastewater Treatment Through Manipulation of the Ecosystem; Water Research, 30, No. 8, p. 1781 1790 (1996).
• Low, E.W. and Chase, H. A.; Reducing Production of Excess Biomass During Wastewater Treatment, Water Research, 33, No. 5, p. 1119 - 1132 (1999).
• Nemerow, N.L. and Dasgupta A.; Industrial and hazardous waste treatment, Van Nostrand Reinhold (1991).
• Springer, A.M.; Industrial Environmental Control Pulp and Paper, 2nd ed, Tappi, Atlanta (1993).
• Tang, C.M.; Downey Brill Jr, E. and Pfeffer, J.T.; Optimization Techniques for Secondary Wastewater Treatment System; Journal of Environmental Engineering, 113, No. 5, p. 935 951 (1987).
• Tang, C.; Downey Brill Jr, E. and Pfeffer, J.T.; Comprehensive Model of Activated Sludge Wastewater Treatment System, Journal of Environmental Engineering, 113, No. 5, p. 952 969 (1987).
• Tang, S.L. and Ellis, K.V.; Wastewater Treatment Optimization Model for Developing World. I Model Testing, Journal of Environmental Engineering, 117, No. 4, p. 501 518 (1991).
• Tang, S.L. and Ellis, K.V.; Wastewater Treatment Optimization Model for Developing World. II Model Testing, Journal of Environmental Engineering, 120, No. 3, p. 611 624 (1994).
• Tchobanoglous, G. and Burton, F.L.; Metcalf & Eddy - Wastewater Engineering: Treatment disposal reuse, McGraw-Hill International Editions, New York (1991).
• Von Sperling, M.; Princípios básicos do tratamento de esgotos, Departamento de engenharia sanitária e ambiental, Universidade Federal de Minas Gerais, Belo Horizonte (1996).

*

To whom correspondence should be addressed

Publication Dates

• Publication in this collection
  16 Mar 2001
• Date of issue
  Dec 2000

History

• Accepted
  18 May 2000
• Received
  19 Nov 1999