Abstract
This work analyzes possible alterations of configuration of an existing multipurpose batch plant for which new production targets and selling profits have been specified. New equipment can be added to the batch plant in the form of a retrofit in order to become a more economical and optimal design. The retrofit problem is posed as a mixed-integer formulation (MILP). The application of the proposed model is illustrated using three examples where can be verified that the method is efficient and of easy application, when compared of the others strategies to solve the retrofit problem.
Multipurpose batch plants; Retrofit; Optimization; MILP
RETROFIT DESIGN OF MULTIPURPOSE BATCH PLANTS WITH MULTIPLE PRODUCTION ROUTES
S.H.V.Carvalho1 and J.I.Soletti1* * To whom correspondence should be addressed
1Departamento de Engenharia Química, Centro de Tecnologia, Universidade Federal de Alagoas,
Campus A.C. Simões, BR 104, Km 96,7, Tabuleiro dos Martins, CEP 57072-970,
Phone (82) 2141280, Fax (82) - 2141625, Maceió - AL, Brazil
E-mail: jsoletti@ctec.ufal.br, scarvalho@ctec.ufal.br
(Received: October 10, 1999 ; Accepted: May 18, 2000)
Abstract - This work analyzes possible alterations of configuration of an existing multipurpose batch plant for which new production targets and selling profits have been specified. New equipment can be added to the batch plant in the form of a retrofit in order to become a more economical and optimal design. The retrofit problem is posed as a mixed-integer formulation (MILP). The application of the proposed model is illustrated using three examples where can be verified that the method is efficient and of easy application, when compared of the others strategies to solve the retrofit problem.
Keywords: Multipurpose batch plants, Retrofit, Optimization, MILP
INTRODUCTION
Retrofitting of a multiproduct batch plants has been the object of studies of Vaselenak et al. (1987) and Fletcher et al. (1991) using the mixed integer non-linear programming formulation. In Vaselenak et al (1987) two possibilities (in phase and out of phase parallel units) for adding new equipment in each batch stage are contemplated. The MINLP formulation by Fletcher et al. (1991) shows that a units may have different operating mode for different products. The heuristic sizing procedure suggested by Yeh and Reklaitis (1987) could accommodate some forms of retrofitting application of single-product plants. Lee et al. (1993) present a heuristic procedure which first determines the positions of adding equipment. Then a nonlinear programming is formulated to obtain their optimal sizes.
Papageorgaki and Reklaitis (1993) investigated the optimal retrofit design of multipurpose batch plants in view of changes in the product demands and/or revisions in the product scale. The model is formulated as a nonconvex MINLP with difficult solution, being computationally intractable.
Carvalho and Soletti (1999) presented a new methodology formulated as a MINLP problem for retrofit design multipurpose batch plant, using the structure of campaigns. This work, in continuity of that presented by Carvalho and Soletti (1999), presents a new MILP problem retrofit designs formulation of an existing multipurpose batch plant.
ASPECTS OF THE RETROFIT DESIGN PROBLEM
The retrofit problem can be considered in two ways: retrofitting to expand the capacity of the existing plant or retrofitting to accommodate a revised product scale.
Retrofit/Expansion
The retrofit/expansion needs is applied when plants require changes in the specifications of the demand of one or more products. Therefore the operational strategic has not to be changed and only the campaign lengths has to be revised leading to modifications in the synthesis structure and equipment sizing. In this way it is important identify the bottlenecks of the process and study the viability to add new equipment in or out of phase.
Retrofit/Revised Product Scale
In this case the project can be severely modified and new products can be added or removed, leading to alterations in the structure of production of the existent products. This condition increases the complexity of the problem, because the addition of new products implies in new routes of production.
MODEL FORMULATION
The plant to be studied has Ej equipment with, j=1,...,M, available in vjs discreet sizes, where s=1,...,nsj represents the number of predefined discreet sizes, associated to each stages j, for each equipment type. Each equipment Ej is related to a cost Cjs. It is assumed that vjs<vj(s+1) for s=1,.. nsj-1. The equipment are divided, in view of type, in G groups. Egg represents the group of available equipment that can exist in a group g, i.e., Egg = { Ej | types of equipment Ej belonging to a same group g}. Mg represents the number of equipment in each group (M = M1 + M2 + M3 ... Mg). It is assumed that any task can be accomplished by any group. A product can be produced through multiple routes involving different combinations of equipment. Batch that use the same route for the production of a certain product are considered identical and they should have the same size. Br indicates the size of the batch to the route r and it corresponds to the sum of the volume of production of the final products. Ni represents the number of routes associated to a product i and, N=NA+NB+.... the number of viable routes for the process. Rpi indicates the group of routes produced by a product i, i. e., Rpi = {r | Routes r that can be produced by a product i}. In a campaign different batch can be produced for one or more products.
Generation of the Routes
The routes that identify a process are obtained by the analysis of all the possible configurations of the system, through a preliminary study of the synthesis of the process, not being object of study of this work. Starting from this identification it becomes necessary the development of a methodology for the selection of the best routes, associated to each product. For a better understanding of the used procedures, will be used a example of which data are presented in the Table 1, Faquir and Karimi (1990).
In this example four different groups are used for the production of four products, divided in the following way: EG1 = {E1 }, EG2 ={ E2,E3,E4}, EG3 = {E5}, EG4 ={E6, E7, E8}. Therefore, M1=1, M2=3, M3=3, M4=3, M5=1, M6=3 e M= å Mi = 10. As the product A requests the groups 1, 2 to realize the tasks 1, 2, respectively, its production can happen in three different ways: routes from 1 to 3, Fig. 1. Defining ERr as being the group of equipment connected to a route r, it is obtained, for the product A, the following groups ER1 ={E1,E2}, ER2 ={E1,E3} and ER3 ={E1,E4}. Applying this methodology to the other products and, defining Ri as being the number of routes for the product i, it is had that RA=3, RB=3, RC=3, RD=3 and R=12, with the possible routes, associated to each product, contained in the following way: RPA = {1,2,3}, RPB = {1,2,3}, RPC = {1,2,3} and RPD = {1,2,3}.
Once selected the routes and the types of equipment for the process, the following stage for the project problem is to find the configuration that represents the minimum cost of investment. Hence, it should be determined the size or kind of equipment, the routes associated to each product, the sizes of the batch relative to each route, and also, to specify a production plan (structure of campaigns) in a period of time. Thus, except for some cases, it is not possible to determine if a certain equipment will exist in the optimal project, becoming necessary to evaluate all the possible configurations of the plant (superstructure), for all the combinations of routes and sizes of equipment.
Mathematical Model
For the formulation of the problem it is necessary the introduction of the binary variable binary yjs, that specifies the existence or not of a certain equipment j, being defined by:

(1)
being vjo=0 if yjo=1 , indicating that the equipment E0 does not exist in the plant.
A series of restrictions is introduced to the problem. The Eq. (2) represents the restriction that imposes the existence of only one size, for each equipment type, associated to the stage j, i. e., the volume of the equipment is calculated by the associated standard size yjs, Eq. (3) and an equipment Ej can be used in any route to which it is requested.

(2)

(3)
The Eq. (4) represents a restriction related to the amount of processed material, defining a minimum capacity for each equipment, in each route
Vj³ FTrjBr"jÎERr, r = 1,..., R,
(4)
where FTrj represents the factor size for the equipment Ej, associated to the route r and, Br represents the size of the batch produced in the route r.
The total time by a route r for production of a product i is represented by Tr. If the preparation and cleaning time of the equipment at the end of the last batch of the campaign be despised, the batch number produced by a route r, in the time of total production Tr, will be approximately Tr/TLr, where TLr represents the cycle time for the route r. This variable can be calculated by the maximum value of time of production in the production sequence, to process a batch in the route r in Ej, that is:

(5)
If qr is the sum of the products produced in the route r, then:
qr = BrTr /TLr , r=1,...,R
(6)
The production of each product i, in whole the routes where will be produced, it should satisfy a specified demand:

(7)
The time of operation Tr, associated to each product in each route, must be inferior to horizont time.

(8)
where CV(r) represents the group of campaigns, associated the routes of production of a product. i.
The horizont time must be smaller or equal to a specified time of production H, Eq. (9).

(9)
The objective function is related to the cost of acquisition of new equipment, Eq. (10).

(10)
The basic difference between the model used for the calculation of the optimal project and the retrofit problem is in the definition of the group of campaigns associated to each route and each product as well as in the specification of the sizes present in the plant.
The previous model described, Eq. (1) to (10), formulated as PNLIM, can be reformulated as a PLIM problem, through the elimination of the non linearitieis of the model, obtained combining Eq. (3), (4) e (6):

(11)
The bilinearity of Eq. (11), regarding the variable qr and yjs, can be eliminated through the introduction of a new variable qrjs, that represents the crossing of products in a same route. The equivalence of the crossing of products is obtained through restrictions, Eq. (12) and (13), that associate the products to the previously specified routes.

(12)
 ,
,
(13)
where Urjs represents the superior limit of the variable qrjs, analytically obtained by the following equation:

(14)
Obtaining of the Campaigns
The new campaigns time will be produced using the procedure developed by Soletti (1997), where all the viable campaigns are identified. This procedure consists of generating a matrix product-route versus equipment, using 1 for the equipment associated to each route otherwise zero, Table 2. A second table, Table 3, is generated multiplying the matrix product-route versus equipment by its transposed. In this table, the null values indicate that there is not conflict of equipment among the marked routes and the non null terms indicate the amount of equipment used by the products associated to each route. In this way, it is possible to identify all the campaigns associated to each product and each route.
Table 4a and 4b were obtained by the analysis of the non null elements of the Table 3, associated to each route. Theses tables do not provide sufficient evidences to show the existence of conflicts among equipment, generating the campaigns, Soletti (1997).
The following restrictions for the campaigns can be identify by the Table 4a and 4b, Eq. (15) to (26):
C9 + C10 + C11 + C12 + C13 + C14 + C15 + C16 ³ TR2
(16)
C17 + C18 + C19 + C20 + C21 + C22 + C23 + C24 ³ TR3
(17)
C1 + C2 + C9 + C10 + C17 + C18 + C23 + C24 ³ TR4
(18)
C3 + C4 + C11 + C12 + C19 + C20 + C27 + C28 ³ TR5
(19)
C5 + C6 + C13 + C14 + C21 + C22 + C29 + C30 ³ TR6
(20)
C3 + C5 + C11 + C13 + C19 + C21 + C27 + C29 ³ TR7
(21)
C1 + C6 + C9 + C14 + C17 + C22 + C25 + C30 ³ TR8
(22)
C2 + C4 + C10 + C12 + C18 + C20 + C24 + C28 ³ TR9
(23)
C15 + C23 ³ TR10
(24)
C7 + C24 ³ TR11
(25)
C8 + C16 ³ TR12
(26)
The additional bounds are:

(27)
where  represents the sizes of the existent equipment in the plant and
represents the sizes of the existent equipment in the plant and  the allowed maximum sizes.
the allowed maximum sizes.
STUDY OF CASES
To verify the efficiency of the proposed method the following three examples are presented here. These examples are based in alterations of configuration of a generic multipurpose plant, Fig. 1. Initially the plant was projected to produce three products A, B and C, in 6.200 hours, with an initial demand of 300.000, 250.000 and 180.000 Kg, respectively. The existent configuration consists of equipment E1, E5, E8, E9 and E10 with capacity of 500 liters and equipment E4 and E6 with 1.000 L. The used routes, as represented in Fig. 1, are R3, R4 and R9.
Example 1
This example analyzes the effect caused by the needs increasing of capacity of production in the plant. An alteration was proposed in the production of the product C from 180.000 to 300.000 Kg. The possible equipment to be used are the originals of the plant, increased of the presented in the Table 4. The possible production routes are 1 to 9, Fig. 1. An optimal solution was obtained the routes R3, R4 and R9, using the equipment E1, E5, E7, E8 and E9 with capacity of 500 l and E4, E6 and E10 with 1000 l, through the campaigns C17, C22 and C26 with 1.788 h, 4.062 h and 350 h, respectively.
Therefore, for the proposed increase capacity of production of the product C was necessary to add a new equipment E7 with 500 L and to increase the capacity of the equipment E10 of 500 to 1000L, in relation to the existent plant.
Example 2
In this case, the effect of the introduction of a new product D was analyzed, with a production of 200.000 Kg. For the proposed problem, it was obtained as solution a configuration with the routes R3, R4, R9 and R12. The equipment E1, E5, E9 and E10 should have a capacity increased of 500 L to 1.000 l and E4 of 1000 L to 2.000 l. The equipment E8 should remain with the same capacity and E6 should not be used. It was identified the campaigns C1, C8, C16, and C18 with the time of operation of 755, 1.883, 636 and 2.925 hours, respectively.
Example 3
In this case it was analyzed the effect of increasing capacity and introduction of a new product, simultaneously. It was increased the production of the product C from 180.000 to 300.000 Kg and it was added a new product D, with esteemed production of 200.000 kg. As solution was obtained a new configuration that uses the routes R3, R4, R9 and R11 with the equipment E1, E3, E5, E8, E9 and E10 with capacity of 1000 l, E4 with 2.000 l and, E6 with 2.500 l. The optimal campaigns obtained were C7, C18 and C24 with the times of 2.960h, 3.120h and 120 h, respectively. In this example it was necessary a total reconfiguration of the plant and an increasing capacity of all equipment.
CONCLUSIONS AND DISCUSSION
The retrofit design problem for a general multipurpose plant is posed as a nonconvex mixed integer nonlinear program (MINLP) and reformulated as a mixed integer linear program (MILP) which accommodates changes in the products demands revisions in the product scale, addition and/or elimination of equipment units, and batch size dependent processing times. The proposed model was developed as an extension of the work presented by Soletti and Carvalho (1999).
The resulting problem was formulated as a MILP model. The modeling language GAMS (Brook et al., 1988) was used executing the code OSL.
Through the analysis of the examples can be verified that the method is efficient and of easy application. On the other hand, the formulation as MILP requests a high time of execution, above 30 minutes in a 200 MHz Pentium processor, to obtain the optimal solution. The advantage of this formulation is the obtaining of only one solution, independent of the initial estimate, fact not verified in the model as MINLP.
NOMENCLATURE
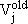
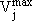
Indice
- Carvalho, S. H. V., Soletti, J. I., "Retrofit Design Of Multipurpose Batch Plants", 2° Congresso de Engenharia de Processos do MERCOSUL, Sep., Santa Catarina, Brazil (1999), p. 586.
- Faquir, N. M., Karimi, I. A., "Design of Multipurpose Batch Plants with Multiple Production Routes", Third International conference on foundations of computer-aided process design, CACHE Corp., Colorado (1990)
- Fletcher, R. H., J. A. J. Johns, W. R., "Flexible Retrofit Design of Multiproduct Batch Plants", Computers & chemical engineering, 12, 843-852 (1991).
- Lee, H.-K. Lee, I.-B., Yang D.. R., Chang K. ,S., "Optimal Synthesis the retrofit Multiproduct Batch Plants", Computers and chemical engineering. 1, 1087-1092 (1993).
- Papageorgaki, S., Reklaitis, G. V., "Retrofitting a General Multipurpose Batch Chemical Plant", Ind. Eng. Chem. Process Des. Dev., 2, 345-362, (1993)
- Soletti J. I. "Tese de Doutorado", Programa de Engenharia Química, Coordenação dos Programas de Pós Graduação em Engenharia, Universidade Federal do Rio de Janeiro, (1997)
- Vaselenak, J. A., Grossmann, I. E., Westerberg, A. W., "Optimal Retrofit Design of Multiproduct Batch Plants", Industrial & engineering chemistry research, 26, 718-726 (1987).
- Yeh, N. C., Reklaitis, G. V., "Synthesis and Sizing of Batch/Semicontinuous Processes: Single Product Plants, Computers and chemical engineering, 11,. 639-654 (1987).
Publication Dates
-
Publication in this collection
16 Mar 2001 -
Date of issue
Dec 2000
History
-
Received
10 Oct 1999 -
Accepted
18 May 2000






