ABSTRACT
The quality of water distribution and the coefficients that express water use efficiency are evaluated from the distribution of the irrigation depth (I). However, a hypothesis has been proposed that it may be more effective to base these analyses on the water depth stored in the soil profile (H), after irrigation. To evaluate this hypothesis, in a very clayey soil, bean was cultivated under irrigation by conventional sprinkling, with four scenarios of water application uniformity. During the crop cycle, irrigations were carried out, scheduled according to a lower limit of soil-water potential. The four scenarios were associated with 64, 144, 192 and 256 experimental points, which were characterized as having excellent (S1), adequate (S2), inadequate (S3) and unacceptable (S4) uniformity, according to obtained values of Christiansen’s uniformity coefficient (CUC) and distribution uniformity coefficient (DUC). At the end of the cycle, harvest was carried out in each grid, obtaining the crop yield. The uniformity of water distribution in the soil negatively impact crop yield only in S4, with an unacceptable water application pattern. The irrigation quality analysis based on values of H is more consistent with the results observed for the crop than the analysis based on the applied water depth.
Keywords:
Conventional sprinkling; Data analysis; Phaseolus vulgaris L.; Water management
RESUMO
A qualidade da distribuição da água e os coeficientes que expressam a eficiência do uso da água são avaliados a partir da distribuição da lâmina de irrigação (I). No entanto, foi proposta a hipótese de que pode ser mais eficaz basear essas análises na lâmina de água armazenada no perfil do solo (H), após a irrigação. Para avaliar esta hipótese, em solo muito argiloso, o feijão foi cultivado sob irrigação por aspersão convencional, com quatro cenários de uniformidade de aplicação de água. Durante o ciclo da cultura foram realizadas irrigações programadas de acordo com um limite inferior do potencial hídrico do solo. Os quatro cenários foram associados a 64, 144, 192 e 256 pontos experimentais, os quais foram caracterizados como tendo uniformidade excelente (S1), adequada (S2), inadequada (S3) e inaceitável (S4), de acordo com os valores obtidos do coeficiente de uniformidade de Christiansen (CUC) e do coeficiente de uniformidade de distribuição (CUD). Ao final do ciclo foi realizada a colheita em cada grade, obtendo-se o rendimento da cultura. A uniformidade da distribuição da água no solo impacta negativamente o rendimento das culturas apenas no S4, com um padrão de aplicação de água inaceitável. A análise da qualidade da irrigação baseada nos valores de H é mais consistente com os resultados observados para a cultura do que a análise baseada na lâmina de água aplicada.
Palavras-chave:
Aspersão convencional; Análise de dados; Phaseolus vulgaris L.; Manejo da água
INTRODUCTION
Irrigation systems are most often evaluated only based on uniformity and efficiency indicators related to the water depth applied on soil surface (Mendoza et al., 2020). However, water extraction by the crop depends on the capacity of the soil to store and conduct water, root system depth, climatic demand and characteristics intrinsic to the crop (Darko et al., 2017). Thus, it is evident that water distribution in the soil profile can be as important as the spatial pattern of water application and should not be ignored. Describing the quality of irrigation performed by a system should be associated with evaluating not only the characteristics of the water application pattern, but also the water distribution in the soil profile explored (Barker et al., 2017).
In the context of irrigated agriculture, a significant number of scientific papers have shown that attention to the water depth stored in the soil, as a basis for assessing uniformity and irrigation efficiency, has been gaining space (Wang et al., 2015; Mohamed et al., 2019; Mendoza et al., 2020). The distributions of values of the variables under analysis in the present study, as well as the possible relationships between them, have been the objects of study of some previous works (Rezende et al., 2002, 2003; Frizzone et al., 2007). However, no statistical technique was employed to analyze the variables referenced in a spatial-temporal domain.
The approaches taken in the cited studies made it possible to arrive at relevant conclusions about the distribution of values of the variables and their interrelationships, but did not allow the data to be explored in all their potentiality, since they were restricted to the use of statistical tools of descriptive analysis and statistical coefficients. This may have limited the understanding of the processes addressed to a level below the possibilities. In view of that, the hypothesis defined for the present study was that an analysis based on plotting the normal probability of the variables studied and their relative differences (Vachaud et al., 1985; Wang et al., 2015; Hara & Gonçalves, 2018; Barker et al., 2017) will enable a more elaborate understanding of their distributions in space as well as their interrelationships. Thus, this study aimed to evaluate the statistical distributions of the variables under analysis, involving the pattern of water application, expressed by the irrigation depth, water distribution in the soil, through the stored water depth and crop yield, expressed by grain yield, as well as the relationship between these variables.
MATERIAL AND METHODS
The experimental area is located in the northwest region of the state of Paraná, Brazil (23° 25' 38” S, 51° 56' 15” W, and 542 m altitude), with soil characterized as NITOSSOLO VERMELHO distroférrico (Ultisol) with clayey texture, with moderate A, nitic B, deep horizon. Soil surface in the area has average slope of 8%. Particle-size fractions of the soil are 122.6 g kg-1 of sand, 120.6 g kg-1 of silt and 756.8 g kg-1 of clay (Hara et al., 2019). A conventional sprinkler irrigation system was structured to have sprinklers with spacing of 12 x 12 m (Scenario 1 - S1); 18 x 18 m (Scenario 2 - S2); 18 x 24 m (Scenario 3 - S3) and 24 x 24 m (Scenario 4 - S4), in order to provide different levels of water application uniformity, above the soil surface (Figure 1). This system was operated to irrigate the bean crop and all data were obtained according to the methodology described in Rezende et al. (2003).
Sprinkler irrigation system including the four scenarios analyzed. Black point is the catch can and cross is the sprinkler installed over the irrigation lateral line.
Evaluation of volumetric water content at -10 kPa (field capacity) and at -1500 kPa (permanent wilting point) for this soil showed values of 0.47 m3m-3 and 0.34 m3m-3, respectively. Considering the crop root system depth of 300 mm, the total available soil water in the root zone (TAW) is 39 mm, the total soil water storage at field capacity (Hfc) is 141 mm and at wilting point (Hwp) is 102 mm. Tensiometers installed at 15 cm depth were used to schedule irrigation. The lower limit of soil water potential used for triggering irrigation events was defined at -50 kPa, which corresponds to the volumetric water content of 0.43 m3 m-3 according to the soil water retention curve (SWRC). From this value and the field capacity, the readily available water (RAW) in the root zone is 12 mm. During the entire experiment, the applied irrigation depth in all irrigation events and all scenarios (i.e., S1, S2, S3 and S4) was set at 12 mm. During the growing season 15 irrigations were carried out, totalizing 180 mm of irrigation water reaching the soil profile. The total rain depth during the period was 150 mm, but the effective rain was not evaluated. During the crop cycle, some irrigations were carried out and precipitation occurred, as shown in Figure 2.
Sheets of water applied indirectly and resulting from rain, during the crop cycle. The highlighted irrigations (marked by an arrow) were followed by rain. Adapted from: Rezende (2001).
As shown, the irrigations that were followed by rain did not have their data used in the analyzes carried out in the work. The remaining irrigations were carried out in order to maintain the first 30 cm of soil with a potential above -50 kPa. Thus, the rain, whenever it occurred, may have been partly used to replace water in this layer and the remainder reached deeper layers of soil. Therefore, the total rainfall was not counted as water available for the crop. To do this, a thorough assessment of the actual rainfall would be necessary, taking into account the circumstances surrounding each event.
Catch cans were installed on a 3 x 3 m regular grid within the area formed by 9 sprinklers (Figure 1), totalizing 64, 144, 192 and 256 points to measure irrigation depth (I), after irrigation, from which the values of uniformity coefficients were obtained. 24 h after, soil water storage in the first 0.30 m layer (H) was measured gravimetrically, close to each catch can. At harvest, crop yield (GY) was evaluated at each of these points, harvesting grains produced in 1 m2 area, around the catch can, and converting the value to kg per hectare (kg ha-1). Mean values of I and H, from 15 irrigations, and GY values were analyzed in this work.
Christiansen’s uniformity coefficient (CUC) and distribution uniformity coefficient (DUC), presented by Darko et al. (2017), were obtained from mean values of I and H. For these variables and for GY values, descriptive statistics were evaluated. For these three variables, normal probability plots were obtained by Statistica software (version 8). The relative difference (dr) defined by Vachaud et al. (1985) was computed by the equation: dr𝑖 = (𝑃𝑖 − 𝑃̅)/𝑃̅, where P is the variable value at “i” spatial position and 𝑃̅ is the average value of P variable, for all measurement points in each one of the four scenarios of this work. Normal probability plots of dr(I), dr(H) and dr(GY) were constructed and compared.
RESULTS AND DISCUSSION
The distributions of the variables evaluated in the present study, which consist of irrigation water depth (I), water depth stored in the soil (H) and crop grain yield (GY), were analyzed using descriptive statistics indicators, which are presented in Table 1, for the four scenarios (i.e. S1, S2, S3 and S4). I and H are mean values obtained in the 15 irrigations performed. The variability of I was always higher than that of H, smoothing the irregularity of water supply to plants, promoted by the redistribution of water in the soil. The larger the spacing between sprinklers, in increasing order of the scenarios, the greater the non-uniformity of both, with the variability of I becoming proportionally greater than that of H. this relationship between emitter distance and uniformity is also reported in other irrigation systems (Wang et al., 2022).
Descriptive statistics for the variables evaluated in the four scenarios (S1, S2, S3 and S4), applied depth (I - mm), total water depth stored in the soil (H = Ɵ Z, in mm) and grain yield (GY - Mg ha-1).
The average crop yield reached the highest value in S2, a condition in which irrigation uniformity is characterized as adequate, and not in S1, characterized as an optimal condition, in terms of irrigation uniformity. On the other hand, in S3, characterized as inadequate irrigation uniformity, the average yield was similar to that obtained in S1. These values point out that crop yield showed a small variation between the scenarios S1, S2 and S3, being above 2.3 Mg ha-1, which is considered adequate in the case of irrigated areas (Osti et al., 2019). Significant reduction in yield was found only in S4, which has irrigation uniformity characterized as unacceptable.
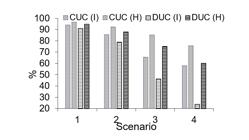
The variability of irrigations performed in each of the four scenarios and of the values of water depth stored in the soil after irrigation was described by the uniformity coefficients usually used in irrigation: CUC and DUC. Figure 3 shows the values of these coefficients. It can be verified that the criterion of CUC greater than 80% is met in S1 and S2, i.e., S3 and mainly S4 are associated with irrigation with inadequate quality, being poor in S3 and unacceptable in S4.
CUC and DUC values for applied water depth (I) and for water depth stored in the soil (H) after irrigation, for the four scenarios evaluated.
A comparison between the scenarios clearly shows that DUC was more sensitive than CUC to the lower extreme values identified in S3 and mainly in S4, which points to its greater sensitivity to extreme values, suggesting that it should be used especially in the context of less uniform irrigations.
In S1, irrigation has high uniformity, with CUC (I) of 94%, resulting in slightly higher uniformity of soil water storage, CUC (H) = 97%. DUC (I) and DUC(H) follow the same pattern and show values higher than 90%, i.e., CUC and DUC coefficients are equivalent in the description of high-quality irrigation. The opposite occurs for low-quality irrigation because, in S3, DUC assumes a value of two thirds the value of CUC, while in S4 it is only one third, revealing that DUC is much more sensitive to lower extreme values, better capturing the occurrence of regions with low water application.
Irrigation in S2 is also of high uniformity, with coefficients showing values in general on the order of up to 10% lower than in S1, but still being characterized as technically adequate. In S2, as in S1, the difference in values between DUC and CUC is small and the uniformity of the water depth stored in the soil profile is greater than that of the applied depth. Thus, in these two scenarios, uniformity is high, both in application and storage. It is inferred that there are optimal conditions for plant development and production in both.
In S3, the poor quality of irrigation is expressed by CUC (I) of 66%, which in principle characterizes it as technically inadequate. Within the current conceptualization, this condition is unfavorable to plant development and production, due to the poor distribution of water on soil surface. DUC (I) proved to be even more sensitive to lower extreme values, falling below 50%, reiterating the poor quality of irrigation. However, DUC (H) and CUC (H) values for soil water storage express a very different situation, with high uniformity. This shows that the processes inherent to the soil, in the circumstances of very clayey soil, were able to promote adequate uniformity of water storage (Ribeiro et al., 2012), from a supply on the surface characterized as highly non-uniform. It remains to be evaluated whether this fact will positively impact plant development and production, which makes the criterion traditionally used in the characterization of irrigation (CUC > 80% for applied depth) questionable.
The fourth scenario, S4, is characterized by an irrigation that can be considered of poor quality, judging by the value of CUC (I) below 60%. The DUC (I) value, however, is even more explicit in characterizing this quality, reaching only 23%, expressing a technically unacceptable condition in terms of irrigation, with areas receiving null water depth, among the sprinklers. In this scenario, although the soil is still able to express a storage uniformity considerably higher than the application uniformity, it is no longer sufficient to guarantee favorable condition, with CUC(H) below 80%, an acceptable reference value. Under these conditions, variability of crop yield due to the water supply in the area is expected.
The normal probability distributions associated with the mean irrigation depth values in each of the four scenarios were evaluated using the Kolmogorov-Smirnov test (K-S). The distribution for S1 is characterized as normal by the test employed (d = 0.119), with a strong concentration of the data around the mean value, on the order of 12 mm (CV = 4.8% in Table 1). The dispersion of the data for S2 shows lower adherence to the line, with greater dispersion. Nevertheless, the K-S test (d = 0.118) allows characterizing the normality of the distribution. For S3 the dispersion grows sharply, but there is still normality of distribution (d = 0.092). Similar dispersion occurs for S4, but in this case normality is rejected by the K-S test (d = 0.146), mainly due to the accumulation of many values close to zero.
According to Rezende et al. (1998), the areas under deficit irrigation (AD), calculated using Walker’s methodology, were 40% for scenario 1, 50% for scenarios 2 and 3 and 54% for scenario 4. The distribution of values of the applied depth, around the mean depth (Im), equal to the required depth (Ir), observed in Figure 3, makes it possible to check the relevance of these values, taking into account the application of water, which promoted the occurrence of similar areas, with deficit (AD) and excess (AE) application.
According to the models used to estimate storage efficiency (Es), in areas with deficit (AD) there would be no loss by percolation, causing all applied water to be stored. In the region with excess application (AE), there would be loss by percolation, reducing the value of the efficiency of water storage in the soil. With normal distribution of values, the higher the slope of the fitted line, the lower the loss by percolation in the area with excess application (AE), leading to a higher value of Es. The values of Es calculated for the situation described by Rezende (2001) were 97.7, 92.9, 83.3 and 78.8%, respectively, for S1, S2, S3 and S3. The analysis of these applied depth distributions suggests that S3 and S4 are similar in terms of water distribution, which could characterize both as poor-quality irrigation, with consequent effects on production.
In evaluation carried out in area irrigated by center pivot, Mendoza et al. (2020) found reduction in CUC (H) when compared to CUC (I), due to the initial soil moisture condition at the beginning of irrigation, as well as a proximity of CUC (H) to the CUC values observed on the surface, when evaluated in deeper layers, between 40 and 60 cm. The authors relate these results to the process of water redistribution in the soil, which depends on the initial moisture.
The capacity of this clay soil to store water in its profile is high, which is why the irregularity of application can be partially smoothed by the water depth stored in the soil profile (H). The normal probability distributions for H values revealed that this smoothing occurred intensely for the first three scenarios, making them similar in terms of distribution. H values follow a normal distribution, according to the K-S test, in the first three scenarios, but not in S4, which was farther from the normal distribution. In S4, the distribution was very different, with about 50% of the area under deficit, including values below the wilting point. On the other hand, much of the area showed very high values of H, one day after irrigation.
In scenario 1, the high uniformity of application is translated into high uniformity of water in the soil profile, in the entire cultivation area, with storage between 150 and 160 mm, 100% of the area above field capacity, after irrigations, which leads to a null area under deficit irrigation (AD), different from that calculated by the model employed (Rezende, 2001).
For S2, although water application is less uniform than in S1, a very similar phenomenon occurred, with the soil showing high storage uniformity, expressed by CUC (H) above 90%, with storage values ranging between 140 and 170 mm. No value was below the storage corresponding to field capacity, maintaining a null value for AD, as observed in S1. Under these conditions, it can be inferred that the irrigation performed in S2 is more convenient from a technical point of view, because the sprinklers are arranged at 18 x 18 m spacing, as opposed to the spacing defined for S1, 12 x 12 m, without any loss of quality, for the application of a 12 mm depth in each irrigation. The system will have lower cost, will require lower installed power and will irrigate with the same quality standard.
The results obtained for S3 are unexpected and interesting. The poor irrigation uniformity in technical terms, with CUC (I) of 66%, well below the technical limit of 80%, was translated by a distribution of water depth stored in the soil with amplitude between 128 and 170 mm, dispersion slightly higher than that observed in S2, and with most positions having values still above the water depth stored under the field capacity condition (Hfc). Also, in S3 it can be inferred that the area under deficit irrigation was virtually null. Although the 18 x 24 m spacing between sprinklers causes low application uniformity, this soil of the experimental area allowed the establishment of adequate uniformity of water storage. Thus, the impacts on crop production indicators may be different from what is expected for poor quality irrigation. The expectation associated with irrigation of this quality, that there would be a high percentage of the area with insufficient irrigation, was not confirmed in this case.
Very different conditions occurred for the fourth scenario. In S4, the poor quality of irrigation, which led to a high percentage of the area with zero applied depth, evidenced by the DUC (I) value of 23%, technically unfeasible in operational terms, was sufficient to impact the pattern of water storage distribution in the soil profile. S4 differed from the other scenarios. This is evident in Table 1, which shows the large dispersion of storage values (H), with maximum of 202 mm, in the regions where excess water was applied, and minimum of 80 mm, in regions that did not receive water application. Since this is a soil with more than 70% clay, the total water depth stored at the wilting point (Hwp) is on the order of 102 mm, causing a high percentage of the area to have lower storage than this. Only in S4 is it possible to visualize what is considered the premise in poor quality irrigation, that is, a percentage of the area among four sprinklers deficiently irrigated, causing the impact of this condition to be more significant in S4 than in the previous three scenarios.
The difference between the four irrigation patterns can be visualized in Figure 4, which presents the minimum, maximum and mean values of the applied depths, as well as the coefficient of variation corresponding to the distribution. In S1, the values are between 12 and 14 mm, with CV of only 5%.
Minimum, maximum and mean values for the distributions in the four scenarios. A) applied depth and coefficient of variation (CV); B) Total water depth stored in the soil (H) and values of Hfc and Hwp.
In S2, the amplitude of values is greater and the CV reaches 15% but, in terms of uniformity, this scenario is much more similar to S1 than the following two, S3 and S4. For these, the CV values are similar and much higher than the previous ones, ranging between 40 and 50%. The amplitude in both is on the order of the maximum value since the minimum is null in S4 and only 0.6 mm in S3. This suggests similar irrigation quality between S1 and S2, characterized as adequate, and between S3 and S4, characterized as inadequate, according to the criteria traditionally employed, especially considering the DUC values. However, the analysis of Figure 4 makes it possible to confirm the pronounced effect of the soil on water distribution, causing the distribution of values of stored water depth in S3 to become very similar to that identified in S1 and S2.
The mean values in the four scenarios are similar, on the order of 150 mm. For this variable, it is evident that scenarios 1, 2, and 3 are very similar, that is, the processes inherent to the water-soil interaction were determinant for S3, despite the low uniformity of irrigation, to be similar to the previous two, in terms of soil water uniformity. It can observed that CV values varied between 1.5% for S1 and only 5.1% for S3, which suggests the perspective that, even in this scenario, the conditions may be adequate for plant development and production, contrary to what would be expected in terms of irrigation quality. It is worth pointing out that, on average, the storage values were slightly above Hfc, with the minimum value slightly below for S3 and equal and higher, for S2 and S1. However, for S4 it was much lower, revealing that in this scenario the processes of water redistribution in the soil were not sufficient to compensate for the inadequate distribution of water on the surface, which is evidenced by a CV of 26% and a minimum value lower than Hwp. In S4, therefore, it is evident that, unlike the others, the distribution of water in the soil profile may compromise the adequacy of the conditions to the crop.
The values of I and H, rendered dimensionless by calculating the relative differences (dr) for each of the distributions, were analyzed by plotting the linearized normal probability, as shown in Figures 5 and 6, respectively.
Normal probability distribution of relative difference (dr) values for I values in the four scenarios and linear models fitted.
Normal probability distribution of the relative difference (dr) values for H values in the four scenarios and linear models fitted.
The models fitted for dr of I (Figure 5) show the decrease in the values of slope (s) as the spacing between sprinklers increases.
The lower the S value, the higher the AD value and the higher the I values at the upper end of the distribution, causing the storage efficiency to be strongly influenced, due to the losses by percolation. Figure 6 shows that the slopes (S) of the linear models fitted for the H distributions are very high compared to the values obtained for I. Similar behavior between system losses and water storage efficiency were obtained of Faria et al. (2019).
The values of S show the considerable capacity of the soil to make H distributions closer to the central tendency values than I distributions, smoothing the irregularities in water application. The most striking effect is observed in S3, where S(H) is more than eight times higher than S(I), showing that the soil is capable of ensuring uniformity of water supply to the crop, despite receiving a technically inadequate irrigation. In S2, S(H) was more than five times higher than S(I), while in S1, because irrigation was already of high uniformity, it was on the order of 3.5 times higher.
In S4, however, the smoothing effect on the irregularities shown by the soil in S1, S2 and S3 was present in a discrete manner, with S(H) being only twice as high as S(I). The relationship between the obtained values of slope and the values of storage efficiency calculated from the applied depths is shown in Figure 7.
Values of Es (%) as a function of the S (I) and S (H) values obtained in the four scenarios.
It is verified that the increase in S (I) values is associated with a potential increase in Es values, calculated based on the distributions of I values, according to Walker’s methodology. However, the S(H) values, presented in Figure 7, show that H distributions are much more concentrated around the mean than I distributions (Figures 5 and 6), which should positively impact the values of efficiency, since this contributes decisively for the values of loss by percolation to tend to be lower. In S4, this contribution of the soil is the least impactful, being much more evident in the other scenarios. This finding suggests that the values of efficiency in irrigation projects should be calculated considering the distribution of water in the soil. This concept is used in precision irrigation systems to increase efficiency in water management (Abioye et al., 2020; Liao et al., 2021; Zhang et al., 2021).
To evaluate the impact of the variables I and H on the crop, grain yield distributions were evaluated using the same analysis strategy. Figure 8 shows the values obtained for the four evaluated scenarios. A piece of information that deserves to be highlighted is the fact that, in the four scenarios, despite the relevant differences between them, the variability of crop yield was virtually the same, with CV on the order of 20%, as can be observed in Figure 8. This reveals that the different conditions inherent to the scenarios promoted variation in the distributions of GY values, impacting the mean value, but practically did not affect their variability.
Minimum, maximum and mean values of crop yield and CV of each distribution, in the four scenarios evaluated.
The minimum values obtained in S1, S2 and S3 are virtually identical, revealing that the uniformity of soil water storage was determinant for crop development and production. For these three scenarios, the maximum values are also very similar, but in S3 this maximum value was even higher. It is important to note that the maximum GY values were obtained in this scenario, which has uniformity of application that can be characterized as unacceptable, in operational terms. Nevertheless, the highest mean value was identified in S2, which shows a concentration of slightly higher values in this scenario compared to S1 and S3. This shows that the excellent uniformity inherent to S1 did not ensure better conditions for the crop, suggesting that this excellence is unnecessary, in practical terms, for this soil. On the other hand, it can be seen that S3, with its poor uniformity of application, proved to generate conditions as favorable to the crop as those of S1 and S2, hence presenting itself as the best option from the technical and economic point of view, to perform irrigation for this combination of crop and soil, contrary to the premise that it would be an inadequate pattern of irrigation, established based on the traditionally employed criteria.
The GY values in S4 reveal that the conditions present there were the most unfavorable among the four scenarios, as expected. In S4, the minimum values of the stored water depth after irrigation were substantially below the permanent wilting point. Thus, even if there was rain in a quantity similar to the total amount of water supplied through irrigation to the area, the occurrence of dry spell at the time of flowering, a period of great sensitivity of the bean crop to water deficit, certainly contributed to reducing GY values in these regions, which is confirmed by their lower GY values, 0.8 Mg ha-1, close to 50% of the minimum value found in scenarios 1, 2 and 3.
On the other hand, the maximum values obtained in S4 were substantially below the maximum values obtained in the other three scenarios. The analysis in Figure 6 reveals that the maximum H values are the highest in this scenario, compared to the other ones. Thus, the maximum GY values, lower in S4, did not occur due to lack of water. Therefore, this suggests that they may have occurred due to an antagonistic effect, because an excess of water in this very clayey soil, with macroporosity generally less than 15%, especially in areas with compacted soil, may have caused restrictions on production due to poor aeration (Andrean et al., 2022; Suzuki et al., 2022). Thus, although the greatest variability of the water depth stored in the soil was found in S4, there was no correspondingly greater variability of GY, because the restrictions were established both in regions with water deficit and in regions with water excess.
The distributions of GY values in the four scenarios were also evaluated by analyzing the normal probability distributions associated with the respective relative differences (dr), as shown in Figure 9.
Normal probability distribution of the relative difference (dr) values for GY values in the four scenarios and models fitted.
The slopes of the lines for the four scenarios are virtually the same, which suggests that not even the strong non-uniformity inherent to S4 significantly impacted the distribution of GY values, despite having caused the absolute values of GY and, consequently, its mean, to retreat compared to the other scenarios. It is also evident that lower and upper extreme values tended to move away from the normal probability line, for all scenarios, which is associated with irregularities in crop production related to factors other than water.
A production function for the bean crop in this soil should, therefore, have a curvature so that the maximum yield as a function of the water factor level should be close to H values corresponding to the field capacity (Hfc), as expected. For substantially lower values, which occurred only in S4, yield was severely impacted, being reduced to almost half of the minimum values identified in S1, S2 and S3, in which there was no water restriction in the soil. On the other hand, the high values of water depth applied in S4, to provide the mean depth, produced a condition of excess water in the soil in a proportionally extensive region, situating these H values above the point of maximum yield, because it is well above Hfc, leading to GY values lower than the maximum inherent to the crop.
CONCLUSIONS
For the conditions of the present study, with the bean crop grown in a very clayey soil, with high water retention capacity, and supplemental irrigation, crop yield did not respond to changes in the water application uniformity pattern, between the conditions characterized as excellent (CUC(I) = 94% in S1), adequate (CUC(I) = 85% in S2) and poor (CUC(I) = 66% in S3).
Only with a water application pattern characterized as very poor (CUC(I) below 60% in S4) was the uniformity of water distribution in the soil compromised to the point of negatively impacting yield in a substantial manner.
Factors intrinsic to the soil in question ensured a resilience that made it able to provide plants with a uniformity of stored water depth high enough (CUC(H) = 85% in S3) to keep the average yield virtually unchanged, even for application with unacceptable uniformity according to current criteria.
In each scenario, the soil promotes higher values of S(H) than of corresponding S(I), highlighting the need to consider the distributions of H in the calculations of efficiencies inherent to irrigation.
This work revealed that the evaluation of soil water storage uniformity is important and should be considered in the design and assessment of sprinkler irrigation systems. Depending on the physical characteristics of the soil, a below-normal application uniformity may lead to no restrictions on the performance of certain crops.
REFERENCES
-
Abioye, E. A., Abidin, M. S. Z., Mahmud, M. S. A., Buyamin, S., Ishak, M. H. I., Rahman, M. K. I. A., Otuoze, A. O., Onotu, P., & Ramli, M. S. A. (2020). A review on monitoring and advanced control strategies for precision irrigation. Computers and Electronics in Agriculture, 173, 105441. http://dx.doi.org/10.1016/j.compag.2020.105441
» http://dx.doi.org/10.1016/j.compag.2020.105441 -
Andrean, A. F., Rezende, R., Soares Wenneck, G., Souza Terassi, D., Vila e Villa, V., Maldonado da Silva, L. H., & Faria Nocchi, R. C. (2022). Air over irrigation system benefits qualitative production of cantaloupe melon in a protected environment. Fruits, 77(5), 20. http://dx.doi.org/10.17660/th2022/020
» http://dx.doi.org/10.17660/th2022/020 -
Barker, J. B., Franz, T. E., Heeren, D. M., Neale, C. M. U., & Luck, J. D. (2017). Soil water content monitoring for irrigation management: A geostatistical analysis. Agricultural Water Management, 188, 36-49. http://dx.doi.org/10.1016/j.agwat.2017.03.024
» http://dx.doi.org/10.1016/j.agwat.2017.03.024 -
Darko, R. O., Shouqi, Y., Junping, L., Haofang, Y., & Xingye, Z. (2017). Overview of advances in improving uniformity and water use efficiency of sprinkler irrigation. International Journal of Agricultural and Biological Engineering, 10(2), 1-15. http://dx.doi.org/10.3965/j.ijabe.20171002.1817
» http://dx.doi.org/10.3965/j.ijabe.20171002.1817 -
Faria, L. C., Norenberg, B. G., Colombo, A., Dukes, M. D., Timm, L. C., & Caldeira, T. L. (2019). Irrigation distribution uniformity analysis on a lateral-move irrigation system. Irrigation Science, 37, 195-206. http://dx.doi.org/10.1007/s00271-019-00619-5
» http://dx.doi.org/10.1007/s00271-019-00619-5 -
Frizzone, J. A., Rezende, R., Gonçalves, A. C. A., & Helbel Júnior, C. (2007). Produtividade do feijoeiro sob diferentes uniformidades de distribuição de água na superfície e na subsuperfície do solo. Engenharia Agrícola, 27(2), 414-425. http://dx.doi.org/10.1590/S0100-69162007000300010
» http://dx.doi.org/10.1590/S0100-69162007000300010 -
Hara, A. T., & Gonçalves, A. C. A. (2018). Estabilidade temporal da variabilidade espacial da umidade do solo obtida no campo e no laboratório. Revista Brasileira de Agricultura Irrigada, 12(6), 3069-3077. http://dx.doi.org/10.7127/RBAI.V12N6001028
» http://dx.doi.org/10.7127/RBAI.V12N6001028 -
Hara, A. T., Gonçalves, A. C. A., Domingues, J. V. S., Hashiguti, H. T., Rezende, R., & Bortoluzzi, D. D. (2019). Estrutura espacial do armazenamento de água no solo na presença de cobertura vegetal. Revista Brasileira de Agricultura Irrigada, 13(2), 3358-3368. http://dx.doi.org/10.7127/rbai.v13n2001056
» http://dx.doi.org/10.7127/rbai.v13n2001056 -
Liao, R., Zhang, S., Zhang, X., Wang, M., Wu, H., & Zhangzhong, L. (2021). Development of smart irrigation systems based on real-time soil moisture data in a greenhouse: proof of concept. Agricultural Water Management, 245, 106632. http://dx.doi.org/10.1016/j.agwat.2020.106632
» http://dx.doi.org/10.1016/j.agwat.2020.106632 -
Mendoza, C. J., Carbonell, J. A., & Lasso, J. J. (2020). Comparison of surface and subsurface water distribution uniformity under center pivot irrigation system for sugarcane in Colombia. Sugar Tech, 22, 1032-1037. http://dx.doi.org/10.1007/s12355-020-00864-5
» http://dx.doi.org/10.1007/s12355-020-00864-5 -
Mohamed, A. Z., Peters, R. T., Zhu, X., & Sarwar, A. (2019). Adjusting irrigation uniformity coefficients for unimportant variability on a small scale. Agricultural Water Management, 213, 1078-1083. http://dx.doi.org/10.1016/j.agwat.2018.07.017
» http://dx.doi.org/10.1016/j.agwat.2018.07.017 -
Osti, A. M., Dallacort, R., Tieppo, R. C., Grzebieluckas, C., & Conceição, A. M. (2019). Rentabilidade do milho e do feijão submetido a diferentes lâminas de irrigação em Mato Grosso. Revista de Economia e Sociologia Rural, 57(4), 505-518. http://dx.doi.org/10.1590/1806-9479.2019.186329
» http://dx.doi.org/10.1590/1806-9479.2019.186329 - Rezende, R. (2001) Efeito da qualidade da irrigação em variáveis de produção e de crescimento da cultura do feijoeiro (Phaseolus vulgaris L.) (Tese de doutorado). Piracicaba, ESALQ/USP.
-
Rezende, R., Andrade Gonçalves, A. C., Lourenço de Freitas, P. S., Frizzone, J. A., Tormena, C. A., & Bertonha, A. (2002). Influência da aplicação de água na uniformidade da umidade no perfil do solo. Acta Scientiarum. Agronomy, 24(5), 1553-1559. http://dx.doi.org/10.4025/actasciagron.v24i0.2419
» http://dx.doi.org/10.4025/actasciagron.v24i0.2419 -
Rezende, R., Frizzone, J. A., Gonçalves, A. C. A., & Freitas, P. S. L. (1998). Influência do espaçamento entre aspersores na uniformidade de distribuição de água acima e abaixo da superfície do solo. Revista Brasileira de Engenharia Agrícola e Ambiental, 2(3), 257-261. http://dx.doi.org/10.1590/1807-1929/agriambi.v2n3p257-261
» http://dx.doi.org/10.1590/1807-1929/agriambi.v2n3p257-261 -
Rezende, R., Gonçalves, A. C. A., Frizzone, J. A., Freitas, P. S. L., Bertonha, A., & Helbel Junior, C. (2003). Uniformidade da lâmina de irrigação, da umidade do solo e da produção da cultura do feijoeiro, espacialmente referenciadas. Acta Scientiarum. Agronomy, 25(2), 425-437. http://dx.doi.org/10.4025/actasciagron.v25i2.2055
» http://dx.doi.org/10.4025/actasciagron.v25i2.2055 - Ribeiro, M. D., Deus, F. P., Barbosa, E. A., Feitosa, D. R. C., Tuta, N. F., Gonçalves, I. Z., & Matsura, E. E. (2012). Soil moisture uniformity for different spacing in a conventional sprinkler irrigation system. Irriga, (Special Issue), 220-233.
-
Suzuki, L. E. A. S., Reinert, D. J., Alves, M. C., & Reichert, J. M. (2022). Medium-term no-tillage, additional compaction, and chiseling as affecting clayey subtropical soil physical properties and yield of corn, soybean and wheat crops. Sustainability, 14(15), 9717. http://dx.doi.org/10.3390/su14159717
» http://dx.doi.org/10.3390/su14159717 - Vachaud, G., Passerat de Silans, A., Balabanis, P., & Vauclin, M. (1985). Temporal stability of spatially measured soil water probability density function. Soil Science Society of America Journal, 49, 822-827.
-
Wang, S., Ji, P., Qiu, X., Yang, H., Wang, Y., Zhu, H., Wang, M., & Li, H. (2022). Effect of border width and micro-sprinkling hose irrigation on soil moisture distribution and irrigation quality for wheat crops. Applied Sciences (Basel, Switzerland), 12(21), 10954. http://dx.doi.org/10.3390/app122110954
» http://dx.doi.org/10.3390/app122110954 -
Wang, T. J., Wedin, D. A., Franz, T. E., & Hiller, J. (2015). Effect of vegetation on the temporal stability of soil moisture in grass-stabilized semi-arid sand dunes. Journal of Hydrology (Amsterdam), 521, 447-459. http://dx.doi.org/10.1007/s11119-009-9119-z
» http://dx.doi.org/10.1007/s11119-009-9119-z -
Zhang, J., Guan, K., Peng, B., Jiang, C., Zhou, W., Yang, Y., Pan, M., Franz, T. E., Heeren, D. M., Rudnick, D. R., Abimbola, O., Kimm, H., Caylor, S., Good, S., Khanna, M., Gates, J., & Cai, Y. (2021). Challenges and opportunities in precision irrigation decision-support systems for center pivots. Environmental Research Letters, 16, 053003. http://dx.doi.org/10.1088/1748-9326/abe436
» http://dx.doi.org/10.1088/1748-9326/abe436

 Effects of applied water depth and soil water storage uniformity on irrigation quality and crop yield
Effects of applied water depth and soil water storage uniformity on irrigation quality and crop yield