On the localization of the gravitational energy

On the localization of the gravitational energy

N. Pinto Neto and P. I. Trajtenberg

Centro Brasileiro de Pesquisas Físicas - CBPF

Rua Xavier Sigaud, 150 - cep 22290-180 - Rio de Janeiro, RJ - Brazil,

E-mail [e-mail]

Received 26 August, 1999

Using a formalism introduced by Feynman, Deser, Grishchuk, Petrov and Popova, the pseudotensors, such as de.ned by Einstein, Tolman, Landau/Lifshitz and Møller, are expessed as gauge dependent tensors in a background space, as the gravitational energy-momentum tensor of Deser, Grishchuk, Petrov and Popova. Using a result obtained by Virbhadra for the energy density in the Reissner-Nordström spacetime, it is shown that the action of these gauge transformations on the above tensorial expressions is the same as the action of the coordinate transformations on the equivalent pseudotensorial expressions, meaning that these tensors can be set to zero at a point by a suitable choice of gauge transformation.

I Introduction

From the advent of General Relativity (GR) theory, various methods have been proposed to deduce the conservation laws that characterize the gravitational systems. In an initial phase, which extended until the middle of the 50's, predominated in the literature the so called pseudotensorial formalism [1]. In this formalism, the conservation laws are expressed, as usual, through the continuity equations

where the conserved quantity 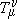refers to the local flux and density of energy and momentum of gravitational systems which may include, in general, both the matter contribution through its energy-momentum tensor 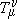, and the gravitational field contribution, here represented by the term t_mⁿ:

An essential property of this formalism is that, contrary to the matter contribution, the gravitational term is not a tensor and admits no homogeneous laws of transformation under coordinate transformations, which justifies its designation, like

itself, as the energy-momentum pseudotensor.

In effect, according to a generally accepted interpretation by the authors which built this formalism, the conservation laws (1) represent a fundamental physical process, whose dynamical description does not depend on the choice of the coordinate system. However, the invariance of the conservation laws (1) implies that the transformation laws of

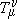must not be homogeneous and this inhomogeneity is related to the gravitational term, since the matter contribution is a true tensor density term.

On the other part, the presence of the inhomogeneous term in the transformation law of

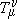makes it possible to annul the gravitational term locally, i.e., at one given point. This property is consistent with the Equivalence Principle according to which the gravitational field can be locally eliminated if we adopt a coordinate system adapted to an observer in free fall at a point. Reciprocally, in flat space-time, where there is no gravitational field, the gravitational term will not be zero when expressed in an arbitrary coordinate system which is not cartesian. Hence, in the pseudotensorial formalism it does not make sense to ask if the gravitational energy density is zero or not at a single point, since this concept depends on the coordinate system. In other words, the pseudotensorial formalism cannot attribute a meaning to the localization of the energy and momentum of a gravitational system which is absent of ambiguities.

Furthermore, the conservation laws (1) do not determine the conserved quantity 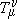univocally. In effect, the conservation condition (1) allows us to express 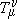through a given anti-symmetric potential function, or superpotential H_m^[nl], according to the following relation:

However, if is a new function (not necessarily anti-symmetric), which differs from by a term , whose divergence or double divergence is identically zero, that is, such that

then, the quantity

defined through this new superpotential is also conserved:

Using this freedom on the choice of the superpotential, authors like Einstein, Tolman, Landau, Lifshitz and Møller arrived through different methods at the following superpotentials:

where ^mn = g^mn is the inverse of _mn and k is the Einstein constant. Because of the inherent ambiguities of the pseudotensor approach, many other proposals for the definition of the gravitational energy-momentum local density have been made. Among them we can cite the Komar definition [2], the Deser, Grishchuk, Petrov and Popova(DGPP) definition [3] and the Brown-York definition¹ [4]. The Komar definition seems to be more adequately related to the notion of gravitational mass then to the notion of energy (see Ref. [6]) The Brown-York definition is not in fact a local but a quasi-local definition. The DGPP definition succeeds to build a local gravitational energy-momentum tensor by describing gravitation as a spin two field propagating in a Ricci-flat fixed spacetime, but it suffers from a gauge ambiguity.

In this paper we will examine in more detail the gauge ambiguity of the DGPP definition. We will show that this ambiguity is nothing but the coordinate transformation ambiguity of the pseudotensors translated to the DGPP language. In fact, the DGPP energy-momentum tensor itself is a new energy-momentum pseudotensor if we write it in the geometrical language. Reciprocally, we can write all pseudotensors as tensors in the DGPP approach, all of them possessing the same gauge ambiguity.

This paper is organized as follows: In section I the DGPP theory is briefly discussed and its expression for the energy-momentum tensor is deduced. In section II we show how the pseudotensors can be expressed as tensor fields, being however, like the DGPP energy-momentum tensor, gauge dependent. In section III, using a result obtained by Virbhadra, it is shown that the gauge dependence of the pseudotensors is equivalent to the dependence with respect to the choice of the coordinate system in GR. We conclude in section IV, with some comments and discussions.

II The DGPP formalism

In the DGPP formalism the gravitational field 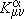and the gravitational potential h^mn can be treated as tensor fields defined in a certain Riemannian background spacetime previously fixed, characterized by the background metric g_mn and by the background connections so that

and

The background space must be Ricci-flat, i.e.,

= 0, in order for the theory be equivalent to GR

In term of the tensor fields defined on (10) and (11), the Einstein/Hilbert action for the gravitational field can be expressed as:

where

and

The semi-colon (;) represents the covariant derivative with respect to the background connections. We have omitted in the lagrangian (12) the terms

which do not contribute to the variation of the action: L₀ and L₁ because of Ricci-flatness, and L₂ because it is a total divergence.

The dynamical equations for the gravitational field can be obtained by varying the DGPP action (12) with respect to the fields

^mn and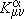 resulting in the following equations for

^mn and :

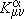and

where

and

The energy-momentum tensor of the gravitational field described by the action (12) can be calculated as usual, by varying the DGPP lagrangian with respect to the background metric, yielding

which is just the right-hand-side term of equation (17) for the gravitational field. Combining the above equations, it is possible to write the energy-momentum of the gravitational field as:

Hence, in the DGPP prescription, the gravitational term can be expressed as a tensor with respect to the coordinate transformations on the background space.

The theory can be extended to include the matter contribution. If L^(m) is the Lagrangian associated with the matter fields the corresponding energy-momentum tensor will be defined, in analogy with (21) as:

Admitting the hypothesis of minimal coupling between the matter and the gravitational field, the free field equation (17) can be generalized to the form:

with and t_mn defined by (19) and (21).

The symmetry properties of

imply in the identity

which results, according to (24), in the covariant energy-momentum conservation laws for the matter plus the gravitational field:

Hence, in the DGPP formalism the invariance of the conservations laws with respect to coordinate transformations is compatible with the tensor nature of the conserved quantities, unlike the pseudotensorial formalism.

III The pseudotensors in the DGPP formalism

It will be shown in this section how the pseudotensors, defined originally in term of the Einsten metric g_mn and its derivatives may be fully expressed in term of the elementary tensor fields h^mn and 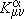defined in the DGPP formalism.

Consider first the original expressions of the pseudotensors in term of the metric g_mn:

Defined as fields on the DGPP background space the pseudotensors, at each point, can be written in a local inertial coordinate system in which the connections are zero at a point and where the covariant derivatives are ordinary derivatives. To express the pseudotensors in an arbitrary coordinate system we can use the background connection

(see eq. (11)) to replace ordinary derivatives by covariant derivatives.

For the Landau/Lifshitz pseudotensor one obtains, in an arbitrary coordinate system, the covariant form:

Replacing in the above expression the definition (10), it results that

where

is the DGPP energy-momentum tensor of matter plus the gravitational field (see equations (19), (24) and (26)). Hence, in the DGPP formalism, the Landau/Lifshitz pseudotensor can be written in tensorial form as was already recognized in reference [3].

For the pseudotensors of Einstein/Tolman and Møller, some difficulties can appear due to the presence of the covariant metric density

_mn, which can only be expressed in term of the DGPP field h_mn = g_mag_nbh^ab by means of an infinite series

Such a difficulty can be overcome by using the relation:

Then, we obtain for the Einstein/Tolman pseudotensor the expression:

where

is given by

The Einstein/Tolman pseudotensor becomes a tensor density of weight 1 in the DGPP formalism. Similarly, for the Møller pseudotensor we get

which is also a tensor density.

Hence, all the pseudotensors admit a purely tensorial representation in the DGPP formalism. We would like to remark that the procedure of replacing the ordinary derivative by the covariant one yields nontrivial results (non null tensors) only in the DGPP framework, where the background connection , instead of is used, so that in this case the covariant derivative of g^mn is not zero.

IV Gauge dependence in the DGPP formalism

If the gravitational energy-momentum pseudotensors can be written as tensors in the DGPP formalism, like the DGPP energy-momentum tensor itself, where do reside the ambiguities in the definition of localized energy in GR in the DGPP approach? We must remember that the DGPP framework is just an alternative view of the same theory, i.e., GR. The answer comes if we note that the coordinate transformation invariance of GR is translated to invariance under gauge transformations on h^mn and 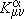in the DGPP formalism.

In effect, consider the infinitesimal coordinate transformation x¢^a = x^a + x^a(x), which changes the functional form of ^mn as

where the Lie derivative £_x⁽¹⁾

^mn is given by

In the case of a finite transformation, the change in

^mn is given by

where £_x^(k) is the Lie derivative of order k defined as

Substituting in (40) the definition (10) we get

The transformed metric density can be decomposed in two distinct ways:

and

where, by comparison with (42) one gets

and

On the form (43) the transformation acts only in the field

^mn, letting invariant the background metric g^mn(x). In this sense, one can interpret the transformation (45) as a pure gauge transformation.

Analogously the pure gauge transformation for the field 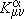(x) is

while for the case which correspond to the transformation (46) we have

It is possible to show that the dynamical equations for the gravitational field (17) are invariant under the transformations (45) and (48) supposing that the background space is Ricci-flat. [3]

On the form (44), (46), (47) and (49) however, the transformation is not a pure gauge transformation , since it acts on the field as well as on the background metric. In fact, these are the usual transformations on tensorial fields resulting from a general mapping of the manifold on which they are defined. Hence, all tensors in the manifold, in particular the energy-momentum tensors defined in the last section, will transform in the usual homogeneous way:

However, the situation is completely different for the case of transformations (45) and (48). The tensors do not transform in the usual way (50) but contains extra inhomogeneous terms which brings the possibility of annulling them. The DGPP energy-momentum tensor, for example, transform in this case according to:

where

^L_mn is the operator which when acting on h^ab yields expression (19). Hence, it is always possible to find gauge transformations (45) and (48) which makes the energy-momentum tensors defined previously to be null. This is the analogue in the DGPP approach to what happens with the pseudotensors in GR.

To illustrate in more detail what happens in the DGPP approach, we will investigate a specific example, taking the DGPP and Landau/Lifshitz energy-momentum tensors, and comparing their transformations under gauge and coordinate transformations in the field and geometrical frameworks, respectively. Initially, let us express the Reissner-Nordström solution in the asymptotically Minkowiskian coordinate system (T, x, y, z) as:

where B = 1 - and r² = x²+y²+z² > r²₀, with r₀ representing the Reissner-Nordström event horizon. Using this coordinate system, the pseudotensors are calculed in Ref. [9] giving the result

where the originals expressions (27), (28) and (29) for the pseudotensors were used. Performing the coordinate transformation on the time variable

the Reissner-Nordström solution can be expressed in the new coordinate system (t, x, y, z) in the form

In this coordinate system the prescriptions of Einstein/Tolman and Møller furnish the same previous results, while the Landau/Lifshitz pseudotensor is given by

revealing, on this form, the ambiguities that characterize the pseudotensorial formalism with regard to the physical meaning of the energy density in gravitational systems.

We can write the two asymptotically flat line element used above in spherical coordinates (r, q, f). For the line element (52) we obtain

whereas for the second line element (55) is given by

One observes that, as before, the metrics (57) and (58) are related by the coordinate transformation (54).

Let us now calculate how the energy-momentum tensors changes in the DGPP formalism. The metric of the background, which is flat spacetime, is given by

From equations (10) and (57) we obtain the following non-null components of the gravitational field:

Considering now the transformed metric (58), and maintaining the line element (59) for the background metric, the new no null potentials h¢^mn(x) will be given by:

It must be stressed that the same background flat metric (59) was used to determine the new potential, in agreement with the form (43) where the background metric is not changed. In this form, the coordinate transformation (54) correspond, in the DGPP language, to a gauge change in h^mn(x) given by (60) to h¢^mn(x) defined in (61) where, by hypothesis, h^mn(x) and h¢^mn(x) are related by the transformation (45).

Completing the calculations by Virbhadra, we now determine the energy density of the Reissner-Nordström solution in the DGPP prescription defined in (22) by

Using first the potential (60) and the background metric (59) one obtain for this prescription

in agreement with the results obtained by Virbhadra using the pseudotensorial formalism. For the gravitational field (61) we get

Hence, just as the Landau/Lifshitz pseudotensor, the DGPP energy-momentum tensor is strongly affected by the transformation. Performing the same calculations for the Landau/Lifshitz energy density in DGPP form (see eq. (31)), we get

for h^mn and

for h¢^mn. These expressions are identical to the expressions obtained by Virbhadra for the Reissner-Nordström energy density in the Landau/Lifshitz prescription, before and after the aplication of the coordinate transformation (54).

Thus, under the action of the gauge transformation h^mn(x) ® h¢^mn(x), with h^mn(x) and h¢^mn(x) given by (60) and (61), the pseudotensor of Landau/Lifshitz transforms itself exactly as if it have suffered the action of the coordinate transformation (54) revealing, in that form, an equivalence between the coordinate transformations in the GR spacetime and this pure gauge transformation defined on the DGPP formalism.

We would like to emphasize that the change in L⁰⁰ from equation (65) to equation (66) is not due to the fact that we are dealing with a component of a tensor. This change can be calculated by using the transformations (46) and (47) yielding

which is different from equation (66).

V Conclusion

In this last section we summarize the conclusions about the pseudotensorial and DGPP formalisms based on the results we have obtained in the previous sections.

First, from the relations obtained in section II, and from the definition (32) of the DGPP energy-momentum tensor one conclude that, although having exhibited a gravitational energy-momentum tensor, which is a necessary condition to express a local quantity of energy in a form independent of the coordinate system, the DGPP formalism does not solve, at last, the problem of the localization of the gravitational energy because the DGPP energy-momentum tensor is not invariant under the pure gauge transformation (45), and it can be put to zero under a suitable choice of this kind of transformation. In fact, in the DGPP formalism both the pseudotensors and the DGPP energy-momentum tensor can be defined from tensorial superpotentials U^_mnb, which are gauge dependent and differ between them by certain anti-symmetric tensorial term Y^_mnb so that the conservation laws are not violated.

The expressions below show the tensorial superpotentials in the various prescriptions as well as the relations that can be established between them:

Hence, the fact that the DGPP energy-momentum is a real tensor is not important, since the pseudotensors can also be written as tensors in this formalism. What is crucial is the dependence of all these quantities under the pure gauge transformations (45), (48). Furthermore, according to the results of section IV, these gauge transformations are equivalent to the general coordinate transformations defined on the GR spacetime. Hence, one conclude that in spite of their intrinsic conceptuals differences, the pseudotensorial and DGPP formalisms have analogous properties and therefore constitute essentially equivalent forms to represent the conservation laws of gravitational systems. This does not mean that the DGPP formalism is useless. Note that the manifold mapping group (MMG) is, at the same time, the covariant group and the symmetry group of GR [10]. In this sense, the role of the DGPP formalism is to split these two distinct aspects of the MMG by defining a background metric over which the fields propagate. The covariance role of the MMG manifests itself in the tensorial nature of fields and equations of motion in the DGPP formalism, which is trivial since any theory can be set covariant. The symmetry role of the MMG, which is one of the most important features of GR, appears in the DGPP formalism as the symmetry of the equations of motion under the pure gauge transformation (45). One should also note that if the field h^mn does not always appear together with g_mn (and also 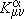with ) in their self-coupling and coupling with matter, the theory looses its gauge symmetry, and there is no sense in nullifying the energy-momentum tensor by means of a gauge transformation: the gravitational energy turns out to be localizable. This is because the background metric g_mn is now observable, not only its combination ^mn = ^mn + ^mn, and hence the symmetry group of the theory will no longer be the MMG but the symmetry group of g_mn (e.g., the Poincaré group if it is the flat metric). The theory can not be formulated in geometrical terms, a preferred reference frame is present (the one adapted to g_mn), and the Equivalence Principle is not satisfied (there is at least one type of particle which follows the geodesics of g_mn, not of g_mn as the others). This is the only way to have a notion of localizable gravitational energy in some alternative theory of gravity which necessarily will not satisfy the Covariance Principle (in the sense that the MMG is no more the symmetry group of the theory [10]) and the Equivalence Principle. For an example of a theory constructed on these lines see Ref.[11].

Hence, the DGPP formalism, although equivalent to GR, not only clarify some important aspects of it but also helps us to envisage alternative routes to describe the gravitational field.

References

• [1] J.L. Anderson, Principles of Relativity physics, chap.13, Academic Press (1967).
• [2] A. Komar, Phys. Rev. 113, 934 (1959).
• [3] S. Deser, Self-Interaction and Gauge Invariance, General Relativity and gravitation 1, 9 (1970), and L.P.Grishchuk, A.N. Petrov and A.D. Popova, Commun. Math. Phys. 94, 379 (1984).
• [4] J.D. Brown and J.W. York Jr., Phys. Rev. D47, 1407 (1993).
• [5] J.W. Maluf, "Sparling Two-Forms, The Conformal Factor and The Gravitational Energy Density of The Teleparallel Equivalent of General Relativity'', GRG 30, 413 (1998).
• [6] N. Pinto-Neto and I. Damiăo Soares, Phis. Rev. D 52, 5665 (1995).
• [7] K.S. Virbhadra, Phis. Rev. D42, 2919 (1990).
• [8] K.S. Virbhadra, Phis. Rev. D41, 1086 (1990).
• [9] K.S. Virbhadra, Phis. Letters A157, 195 (1991).
• [10] J.L. Anderson, Principles of Relativity Physics, Chap. 4, Academic Press (1967).
• [11] M. Novello, V.A. De Lorenci and L.R. de Freitas, Ann. of Phys. 254, 83 (1997).

Publication Dates

• Publication in this collection
  17 Oct 2001
• Date of issue
  Mar 2000

History

• Received
  26 Aug 1999