In earlier work [1], we studied an extension of the canonical symplectic structure in the cotangent bundle of an affine space Q = R N, by additional terms implying the Poisson non-commutativity of both configuration and momentum variables. In this article, we claim that such an extension can be done consistently when Q is a Lie group G.
Symplectic Mechanics; Noncommutative Configuration Space
Modified symplectic structures in cotangent bundles of lie groups
F.J. Vanhecke; C. Sigaud; A.R. da Silva
Instituto de Física, Instituto de Matemática, UFRJ, Rio de Janeiro, Brazil
ABSTRACT
In earlier work [1], we studied an extension of the canonical symplectic structure in the cotangent bundle of an affine space Q = RN, by additional terms implying the Poisson non-commutativity of both configuration and momentum variables. In this article, we claim that such an extension can be done consistently when Q is a Lie group G.
Keywords: Symplectic Mechanics; Noncommutative Configuration Space.
1. INTRODUCTION
As applied to physics, noncommutative geometry is understood mainly in two ways. The first one is the spectral triple approach of A.Connes [2] with the Dirac operator playing a central role in unifying, through the universal action principle, gravitation with the standard model of fundamental interactions. The second one is the quantum field theory on noncommutative spaces [3] with the Moyal product as main ingredient. Besides these, a proposition by several authors [4,5] was made to generalise quantum mechanics in such a way that the operators corresponding to space coordinates no longer commute: [
k,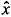 ℓ] ≠ 0 . This was implemented by an extension of the Poisson structure on the cotangent space such that the brackets satisfy {xk, xℓ} ≠ 0. Upon quantisation, the corresponding operators should then also be noncommutative. A particle moving in an affine space AN, has its configuration, in a fixed reference frame, given by an element {xk} of the translation group: Q = RN with cotangent bundle T*(Q) = RN × RN. In [1], we examined such an extension of the canonical symplectic two-form ω0 = dxi ∧ dpi → Ω = ω0 + ωF + ωB:
ℓ] ≠ 0 . This was implemented by an extension of the Poisson structure on the cotangent space such that the brackets satisfy {xk, xℓ} ≠ 0. Upon quantisation, the corresponding operators should then also be noncommutative. A particle moving in an affine space AN, has its configuration, in a fixed reference frame, given by an element {xk} of the translation group: Q = RN with cotangent bundle T*(Q) = RN × RN. In [1], we examined such an extension of the canonical symplectic two-form ω0 = dxi ∧ dpi → Ω = ω0 + ωF + ωB:
This extension is form-invariant under a change of the reference frame lifted to the cotangent bundle:


For a general configuration space Q, a diffeomorphism ø:xi → x'i  øi(x), when lifted to T*(Q), becomes
øi(x), when lifted to T*(Q), becomes
In general B'kℓ is function of both variables {p', x'} and no intrinsic meaning can be given to the particular form of the extension Ω in equation (1.1).
In this work, we show that such an extension is achieved when Q = G is a Lie group. This is possible because the cotangent bundle T*(G) has two distinguished trivialisations, the left- and right trivialisations [7] implemented respectively by the bases of the left- and right invariant differential forms.
In section 2., inspired by the rigid body motion, we use the left trivialisation with left invariant or body-coordinates and construct a left invariant two-form. In the case of constant Fij and Bkℓ fields the ωF term arises from a symplectic one-cocycle, as introduced by Souriau [8,9], and ωB will be automatically left invariant. The constructed two-form Ω is obviously closed but the non degeneracy condition leads in general to a constrained Hamiltonian system. This is examined in more detail for SU(2) in section 3.. Final considerations are made in section 4.. Some elements of Lie algebra cohomology [9, 10] are recalled in the appendixappendix with values in acts with the coadjoint representation ,→ 〈θ(, A one-cochain θ on with values in *, on which acts with the coadjoint representation k, θ ∈ C1 (,*,k), is a linear map θ: → *:u → θ (u). Its components are θα,µ 〈θ(eµ)|eα〉. It is a one-cocycle, θ ∈ Z1(,*,k), if its coboundary, (δ1θ) (u, v) k(u)θ(v)-k(v)θ(u)-θ([u, v]), vanishes. .
2. THE PHASE SPACE {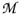 0≡ T*(G), ω0}
0≡ T*(G), ω0}
Let {gα, α = 1,2, ..., N} be coordinates of a group element g ∈ G. Natural or holonomic coordinates of points (g, pg) ∈ T*(G) are obtained using the basis {dgµ} of the cotangent space  (G). They are given by (gα, pµ)hol, where pg = pµ dgµ. Given a pair of dual bases {eα} of the Lie algebra
(G). They are given by (gα, pµ)hol, where pg = pµ dgµ. Given a pair of dual bases {eα} of the Lie algebra 
 *, the differential and pull-back of the left- and right translations (Lg, Rg) define left- and right invariant vector fields and one forms:
*, the differential and pull-back of the left- and right translations (Lg, Rg) define left- and right invariant vector fields and one forms: 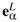 (g)
(g)  Lg*|eeα ,
Lg*|eeα , 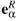 (g)
(g)  |e eα ,
|e eα , 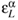 (g)
(g)  -1|gεα ,
-1|gεα , 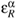 (g)
(g)  -1|gεα. With canonical group coordinates, in terms of Lαβ(g, h)
-1|gεα. With canonical group coordinates, in terms of Lαβ(g, h)  ∂(g h)α/∂gβ and Rαβ (g, h)
∂(g h)α/∂gβ and Rαβ (g, h)  ∂(h g)α/∂gβ, they are explicitely given by:
∂(h g)α/∂gβ, they are explicitely given by:
These bases implement canonical trivialisations of the tangent and cotangent bundle. For the cotangent bundle, which is the arena of symplectic or Hamiltonian formalism, we have a left and a right trivialisation:
They can be viewed as a change of coordinates of a point (g, pg) in T*(G):
In rigid body theory, the coordinates of the left trivialisation are the "body" coordinates, whence the subscript (,)B. The right trivialisation yields "space" coordinates with subscript (,)S. Both are related through the coadjoint representation of G in  *:
*:
Lifting the left multiplication in G to the cotangent bundle yields a group action:  a:T*(G) → T*(G):x = (g, pg)→ y = (ag, p'ag =
a:T*(G) → T*(G):x = (g, pg)→ y = (ag, p'ag =  -1|ag pg). In body coordinates: (
-1|ag pg). In body coordinates: ( a)B:(gα,
a)B:(gα, )B→ ((ag)α,
)B→ ((ag)α, )B. The pull-back of the cotangent projection κ:T*(G) → G:x
)B. The pull-back of the cotangent projection κ:T*(G) → G:x  (g, pg) → g, acting on the {εα(g)} yield
(g, pg) → g, acting on the {εα(g)} yield  a invariant one forms on T*(G) : 〈
a invariant one forms on T*(G) : 〈 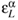 (x)| =
(x)| = 
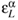 (κ(x)) and the differentials of the left invariant functions
(κ(x)) and the differentials of the left invariant functions  on T*(G) also yield
on T*(G) also yield  a invariant one forms on T*(G). Together they provide a left invariant basis of the cotangent space at x = (gα,
a invariant one forms on T*(G). Together they provide a left invariant basis of the cotangent space at x = (gα,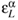 )B ∈ T*(G):
)B ∈ T*(G):
Its dual basis in the tangent space Tx(T*(G)) is given by
The canonical Liouville one-form 〈θ0| = pα 〈dgα| and its associated symplectic two-form ω0 = -dθ0 = 〈dgα|∧ 〈dpα|, are obtained as:
The Hamiltonian vector field associated to a function A(g,πL) on phase space 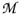 0≡ T*(G), is defined by: ıXω0 = 〈dA|. Its components are:
0≡ T*(G), is defined by: ıXω0 = 〈dA|. Its components are:
With ıYω0 = 〈dB| , the Poisson bracket of dynamical variables: {A, B}0 ω0(X, Y), is obtained explicitely in (gα,
ω0(X, Y), is obtained explicitely in (gα, ) variables as:
) variables as:
In particular, the basic Poisson brackets are:
The flow of a particular observable, the Hamiltonian H(g, πL), determines the time evolution of any observable A(g, πL) by the equation: dA/dt = {A, H}0. We assume a Hamiltonian is of the form H(g, πL) = K(πL) + V(g).
Here, as in rigid body mechanics, the kinetic energy is given by
where Iαβ is the inverse of a constant, positive definite, inertia tensor Iµn in the "body" frame. The potential energy is a function V defined on the group manifold. The Euler equations of motion read:
The first of these equations (2.11) relates the angular momentum  with the angular velocity in the body frame
with the angular velocity in the body frame  :
:
while the second (2.12) takes the classical form
An example of V(g) is given by a gravitational potential energy as follows. Let L = eα Lα be a constant vector in  (the position of the centre of mass in the body frame) and γ = γαεα a constant vector in
(the position of the centre of mass in the body frame) and γ = γαεα a constant vector in  * (the gravitational force in the space fixed frame). The potential energy is defined as:
* (the gravitational force in the space fixed frame). The potential energy is defined as:
where ( | ) denotes the canonical pairing between  and its dual
and its dual  *. To compute 〈dV|
*. To compute 〈dV| 〉 we use the representation of the Maurer-Cartan form:
〉 we use the representation of the Maurer-Cartan form:
D(g-1) dD(g) = D'(g-1dg)
where D is any representation D of G, with derived representation D' of  . In particular, dAd(g) = Ad(g) ad(eµ)
. In particular, dAd(g) = Ad(g) ad(eµ)  (g) and dK(g) = K(g) k(eµ)
(g) and dK(g) = K(g) k(eµ)  (g). This yields:
(g). This yields:
where Γ(g)  K(g-1) γ is the variable gravitational force in the body-fixed frame. Using the above formulae to compute dK(g-1), we obtain:
K(g-1) γ is the variable gravitational force in the body-fixed frame. Using the above formulae to compute dK(g-1), we obtain:
Equation (2.14) reads:
Together with (2.13),
the equations (2.17) and (2.18) form the so-called Euler-Poisson system.
3. MODIFIED SYMPLECTIC STRUCTURE ON T*(G)
In appendix Aappendix with values in acts with the coadjoint representation ,→ 〈θ(, A one-cochain θ on with values in *, on which acts with the coadjoint representation k, θ ∈ C1 (,*,k), is a linear map θ: → *:u → θ (u). Its components are θα,µ 〈θ(eµ)|eα〉. It is a one-cocycle, θ ∈ Z1(,*,k), if its coboundary, (δ1θ) (u, v) k(u)θ(v)-k(v)θ(u)-θ([u, v]), vanishes. it is shown that, if Θ =  Θαβεα ∧ εα ∈ Λ2 (
Θαβεα ∧ εα ∈ Λ2 ( *), obeys the cocycle condition (A.1), then ΘL(g)
*), obeys the cocycle condition (A.1), then ΘL(g)  (1/2) Θαβ
(1/2) Θαβ 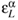 (g) ∧
(g) ∧  (g) is a closed left-invariant two-form on G. Including this closed two-form in the canonical two-form, one obtains another symplectic two-form on T*(G), which, furthermore, is
(g) is a closed left-invariant two-form on G. Including this closed two-form in the canonical two-form, one obtains another symplectic two-form on T*(G), which, furthermore, is  a invariant. So we define:
a invariant. So we define:
The Poisson brackets are also modified and (2.8), (2.9) become:
In particular, the fundamental brackets are:
The modified symplectic structure induces an additional interaction and the Euler equations become:
The relation between the velocity in the body frame and the angular momentum (2.13) is maintained:  = Iµν
= Iµν  , while the second (2.14) takes the interaction into account:
, while the second (2.14) takes the interaction into account:
For a semisimple Lie algebra  , we have Θαβ = - ξµ fµ αβ and we may define a modified Liouville one-form:
, we have Θαβ = - ξµ fµ αβ and we may define a modified Liouville one-form:
and the symplectic two-form reads
This means that such that {gα, p'µ = pµ + ξβ Lβµ (g-1; g)} are Darboux coordinates:
In (gα,  ) coordinates, the Hamiltonian reads
) coordinates, the Hamiltonian reads
and the Euler equations read:
which, obviously are equivalent to (3.4) and (3.12).
4. THE CLOSED TWO FORM ωL
Configuration space coordinates which do not Poisson commute, are obtained through the addition of a left-invariant and closed two-form to (3.1):
With the notation Sαβ ≡ ( fµαβ - Θαβ), we wite ωL in matrix form:
fµαβ - Θαβ), we wite ωL in matrix form:
The degeneracy of (ωL) is examined comsidering the equation
In the bases (2.4), (2.5): Xα  〈
〈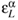 |X〉 , Xµ
|X〉 , Xµ 
 |X〉 and (4.4) reads:
|X〉 and (4.4) reads:
where we introduced the matrices, linear in the momenta:
They are mutually transposed and the products Φ S = S Ψ , ϒ Φ = Ψ ϒ are antisymmetric. The fundamental equation (4.4), defining Hamiltonian vector fields, has a solution if Φ and Ψ have inverses, i.e. if
The matrices ϒ Φ-1 = Ψ-1ϒ and Φ-1S = S Ψ-1 are then also antisymmetric. The Hamiltonian vector fields are obtained as:
The Poisson brackets between the basic dynamical variables are:
For a Hamiltonian H = K + V, the equations of motion are:
Since Φ, Ψ are linear in πL, Δ is a polynomial in πL of degree at most equal to N, the dimension of the Lie group. It defines an algebraic variety in  *:
*:
and its complement
Δ *\Π1 defines a manifold
*\Π1 defines a manifold
with symplectic structure given by ωL, restricted to 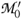 . If it happens that Π1 itself is an algebraic manifold, an imbedded submanifold is obtained:
. If it happens that Π1 itself is an algebraic manifold, an imbedded submanifold is obtained:
with imbedding in
0G× *: j1:
*: j1: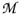 10. The system is then constrained to
10. The system is then constrained to 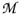 1 and we may look for solutions of (4.4) restricted to
1 and we may look for solutions of (4.4) restricted to 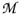 1. Such solutions may exist if further conditions are imposed on the Hamiltonian. To proceed systematically, we follow the algorithm of Gotay, Nester and Hinds [11]. To keep things simple, this will be done in the next section for the semi-simple group SU(2).
1. Such solutions may exist if further conditions are imposed on the Hamiltonian. To proceed systematically, we follow the algorithm of Gotay, Nester and Hinds [11]. To keep things simple, this will be done in the next section for the semi-simple group SU(2).
5. A CASE STUDY: SU(2)
The dynamical variables are functions on
0SU(2) × su(2)*. A basis {eα} of the Lie algebra su(2) may be chosen such that its structure constants are the Kronecker symbols [eα,eβ] = eµ εµαβ. The Killing metric ηαβ εµαν ενβµ= -2 δαβ, provides an isomorphism between su(2) and su(2)*. The metric δαβ with inverse δµν will be freely used to raise or to lower indices. ΘL is written in terms of a magnetic field ξµ as Θαβ = -ξκεκαβ and any antisymmetric ϒ can be written in terms of τλ, a dual magnetic field in momentum space, as Yµν = τλελµν. Defining
εµαν ενβµ= -2 δαβ, provides an isomorphism between su(2) and su(2)*. The metric δαβ with inverse δµν will be freely used to raise or to lower indices. ΘL is written in terms of a magnetic field ξµ as Θαβ = -ξκεκαβ and any antisymmetric ϒ can be written in terms of τλ, a dual magnetic field in momentum space, as Yµν = τλελµν. Defining 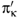
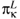 + ξκ, ωL reads:
+ ξκ, ωL reads:
The fundamental equation (4.4): ı|X 〉 ωL = 〈dH| becomes:
Xα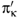 εκαβ - Xβ = Hβ, Xν + Xµτλελµν = Hν
εκαβ - Xβ = Hβ, Xν + Xµτλελµν = Hν
where Hβ  (∂H/∂gα) Lαβ(g, e) , Hν
(∂H/∂gα) Lαβ(g, e) , Hν  (∂H/∂
(∂H/∂  ). The matrices (4.6) are given explicitely by Φ αν
). The matrices (4.6) are given explicitely by Φ αν  C1δαν+ ταπ' ν and Ψµβ
C1δαν+ ταπ' ν and Ψµβ  C1δµβ+ π'µτβ, where C1
C1δµβ+ π'µτβ, where C1 (1-π'·τ). They obey Φαν (δνβ -τνπ'β) = C1δαβ and Ψµβ (δβν- π'βτν) = C1δµν. It follows that (4.5) implies:
(1-π'·τ). They obey Φαν (δνβ -τνπ'β) = C1δαβ and Ψµβ (δβν- π'βτν) = C1δµν. It follows that (4.5) implies:
5.1. The non degenerate case
The determinant of the matrices Φ and Ψ is given by Δ = (C1)2. Obviously the plane Π1 {(g,πL)|(1-π'·τ) = 0} is an algebraic manifold in
{(g,πL)|(1-π'·τ) = 0} is an algebraic manifold in  *. Its complement
*. Its complement 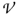 Δ
Δ 
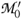 G ×
G × 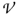 Δ with symplectic structure ωL, retricted to
Δ with symplectic structure ωL, retricted to 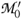 . On
. On 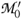 , Φ and Ψ have inverses:
, Φ and Ψ have inverses:
For a Hamiltonian H = K(πL) + V(g), the Hamiltonian vector fields are read off from (5.2) and (5.3) with ensuing equations of motion:
For a purely kinetic Hamiltonian, we obtain:
5.2. The degenerate case
The equation C1≡ (1 - π' · τ) = 0 defines a two dimensional plane Π1 in su(2)*≅ R3. The primary constrained manifold, defined by  1
1
 0SU(2) × su(2)*. On
0SU(2) × su(2)*. On  1, the closed two-form ωL is degenerate and the pairing of π' su(2)* with τ ∈ su(2) equals 1. So |τ 〉 ≠ 0 and, without loss of generality, we take {τα} = {0,0, τ}. In what follows, greek indices {α,β,µ,ν,...} shall vary in {1,2,3}, while latin indices {a, b, m, n,...} assume only the values {1,2}. The imbedding is given by:
1, the closed two-form ωL is degenerate and the pairing of π' su(2)* with τ ∈ su(2) equals 1. So |τ 〉 ≠ 0 and, without loss of generality, we take {τα} = {0,0, τ}. In what follows, greek indices {α,β,µ,ν,...} shall vary in {1,2,3}, while latin indices {a, b, m, n,...} assume only the values {1,2}. The imbedding is given by:
with its differential or push-forward:
The pull-back transforms forms on
0 into forms on 1:
1:
In particular the pull-back of ωL to the five dimensional manifold 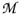 1 is
1 is
The restriction of ωL to 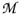 1, not to be confused with its pull-back, is denoted by ωL| 1
1, not to be confused with its pull-back, is denoted by ωL| 1 ωL° j1. In matrix representation:
ωL° j1. In matrix representation:
Let (T
0)| 1 {(x,X) ∈ T0 | x ∈
{(x,X) ∈ T0 | x ∈ 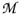 1} be the subbundle of T0 restricted to
1} be the subbundle of T0 restricted to 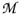 1. Following the GNH algorithm [11], we look for a vector field |X〉 in (T0)| 1, tangent to
1. Following the GNH algorithm [11], we look for a vector field |X〉 in (T0)| 1, tangent to 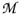 1 and solution of ı|X 〉 ωL| 1 = 〈dH| ° j1. Explicitely :
1 and solution of ı|X 〉 ωL| 1 = 〈dH| ° j1. Explicitely :
Two independent null vectors of ωL| 1, solution of ı|Z〉 ωL| 1 = 0, are given by:
Consistency requires {〈dH|Za〉 = 0} for (a = 1,2) and  = 1/τ.
= 1/τ.
These two equations define a secondary constrained manifold
2⊂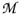 1, on which a particular solution of (??) is
1, on which a particular solution of (??) is
where C23≡  (∂K/∂
(∂K/∂ )-
)- (∂K/∂
(∂K/∂ )-〈dV|
)-〈dV| 〉. The general solution |XG〉 of (??),
〉. The general solution |XG〉 of (??),  , still contains two arbitrary functions ζ1 and ζ2:
, still contains two arbitrary functions ζ1 and ζ2:
This vector must be tangent to
1 and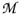 2. This leads to three equations
2. This leads to three equations
If these three equations determine or not the two arbitrary functions ζ1 and ζ2 , will depend on the kinetic energy K(πL) and on the particular form of the potential V(g). If they do so, the system will have a solution. If not, they will define a tertiary constraint manifold 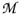 3 and the analysis must proceed.
3 and the analysis must proceed.
6. CONCLUSIONS
In this work, we analysed the consistency of a modification of the symplectic two-form on the cotangent bundle of a group manifold. This was done in order to obtain classical, i.e. Poisson, noncommuting configuration (group) coordinates. This was achieved in the non degenerate case, with the closed two-form ωL which is then symplectic. We do not address here the general quantization problem of such a system and refer e.g. to [12] for a general review on quantization methods. It should be stressed that, whatever the quantisation scheme, any such obtained framework has little to do with non commutative geometry, either in the sense of A.Connes or as a quantum field theory on non-commutative spaces.
(Received on 10 April, 2008)
The one-cocycle σ is called symplectic if Σ(u, v)  〈σ(u)|v〉 is antisymmetric, Σ(u, v) = - Σ(v, u) or Σ[αµ]
〈σ(u)|v〉 is antisymmetric, Σ(u, v) = - Σ(v, u) or Σ[αµ] σα,µ= - σµ,α . Any antisymmetric Θ defined in terms of θ ∈ C1(
σα,µ= - σµ,α . Any antisymmetric Θ defined in terms of θ ∈ C1( ,
, *,k) as Θ[αβ] = θα,β is actually a 2-cochain on
*,k) as Θ[αβ] = θα,β is actually a 2-cochain on  with values in R and trivial representation: Θ ∈ C2(
with values in R and trivial representation: Θ ∈ C2( ,R,0). Furthermore, when θ ∈ Z1(
,R,0). Furthermore, when θ ∈ Z1( ,
, *,k), Θ is a 2-cocycle of Z2(
*,k), Θ is a 2-cocycle of Z2( ,R,0):
,R,0):
In general let Θ =  Θαβεα∧β∈ Λ2(
Θαβεα∧β∈ Λ2( *), obey the cocycle condition (A.1). Acting with
*), obey the cocycle condition (A.1). Acting with  yields the left-invariant two form:
yields the left-invariant two form:
Using the cocycle relation and the Maurer-Cartan structure equations, it is seen that ΘL(g) is a closed left-invariant two-form on G.
When  is semisimple, Θ is exact. Indeed, the Whitehead lemmas state that H1(
is semisimple, Θ is exact. Indeed, the Whitehead lemmas state that H1( , R, 0) = 0 and H2(
, R, 0) = 0 and H2( , R, 0) = 0. In particular, Θ ∈ B2(
, R, 0) = 0. In particular, Θ ∈ B2( ,R,0) is a coboundary and there exists an element ξ of C1(
,R,0) is a coboundary and there exists an element ξ of C1( , R, 0) ≡
, R, 0) ≡  * such that Θ(u, v) = (δ1(ξ))(u, v) = - ξ([u, v]) or
* such that Θ(u, v) = (δ1(ξ))(u, v) = - ξ([u, v]) or
The constant vector ξ ∈ T*( ) is the analogue of a magnetic field in the abelian case G ≡ R3.
) is the analogue of a magnetic field in the abelian case G ≡ R3.
References
- [1] F.J.Vanhecke, C.Sigaud and A.R.da Silva, Noncommutative Configuration Space. Classical and Quantum Mechanical Aspects, arXiv:math-phys/0502003 and Braz.J.Phys.36,no IB,194(2006)
- [2] A.H.Chamseddine and A.Connes, The Spectral Action Principle, Commun.Mat.Phys.186,731(1997)
- [3] M.R.Douglas and N.A.Nekrasov, Noncommutative Field Theory, Rev.Mod.Phys.73, 977(2001)
- [4] C.Duval and P.A. Horváthy, The exotic Galilei group and the "Peierls substitution", Phys.Lett.B 479,284(2000)
- [5] P.A. Horváthy, The Non-commutative Landau Problem, Ann.Phys.299,128(2002)
- [6] P.A. Horváthy and M.S.Plyushchay, Anyon wave equations and the noncommutative plane, Phys.Lett.B 595,547(2004)
- [7] R. Abraham and J.E. Marsden, Foundations of Mechanics, Benjamin,1978
- [8] J-M. Souriau, Structure des systèmes dynamiques,Dunod,1970.
- [9] P.Liberman and Ch-M.Marle, Symplectic Geometry and Analytical Mechanics, D.Reidel Pub.Comp.,1987
- [10] J.A. de Azcárraga and J.M.Izquierdo, Lie groups, Lie algebras, cohomology and some applications in physics, Cambridge Univ.Press,1998.
- [11] M.J. Gotay, J.M. Nester and G. Hinds, Presymplectic manifolds and the Dirac-Bergmann theory of constraints, J.Math.Phys.19,2388(1978).
- [12] S.Twareque Ali and Miroslav Engliš, Quantization Methods: A Guide for Physicists and Analysts, Rev.Math.Phys.17,381(2005).
appendix
 with values in
with values in 
 acts with the coadjoint representation
acts with the coadjoint representation  ,
,
 →
→ 
 〈θ(
〈θ( ,
,

A one-cochain θ on  with values in
with values in  *, on which
*, on which  acts with the coadjoint representation k, θ ∈ C1 (
acts with the coadjoint representation k, θ ∈ C1 ( ,
, *,k), is a linear map θ:
*,k), is a linear map θ:  →
→  *:u → θ (u). Its components are θα,µ
*:u → θ (u). Its components are θα,µ  〈θ(eµ)|eα〉. It is a one-cocycle, θ ∈ Z1(
〈θ(eµ)|eα〉. It is a one-cocycle, θ ∈ Z1( ,
, *,k), if its coboundary, (δ1θ) (u, v)
*,k), if its coboundary, (δ1θ) (u, v)  k(u)θ(v)-k(v)θ(u)-θ([u, v]), vanishes.
k(u)θ(v)-k(v)θ(u)-θ([u, v]), vanishes.

 Modified symplectic structures in cotangent bundles of lie groups
Modified symplectic structures in cotangent bundles of lie groups


































































