Abstract
The construction of theta-local superfield Lagrangian BRST quantization in non-Abelian hypergauges for generic gauge theories based on the action principle is examined in the case of reducible local superfield models (LSM) on the basis of embedding a gauge theory into a special theta-local superfield model with antisymplectic constraints and a Grassmann-odd time parameter theta. We examine the problem of establishing a new correspondence between the odd-Lagrangian and odd-Hamiltonian formulations of a local LSM in the case of degeneracy of the Lagrangian description with respect to derivatives over theta of generalized classical superfields A I(theta). We also reveal the role of the nilpotent BRST-BFV charge for a formal dynamical system corresponding to the BV-BFV dual description of an LSM.
Lagrangian (superfield) BV quantization; Odd Lagrangian and Hamiltonian formulations; Second-class constraints; Reducible multi-level non-Abelian hypergauges
REGULAR ARTICLES
Reducible gauge theories in local superfield Lagrangian BRST quantization
D. M. GitmanI; P.Yu. MoshinI, II; A.A. ReshetnyakIII
IInstituto de Física, Universidade de São Paulo, Caixa Postal 66318-CEP, 05315-970 São Paulo, S.P., Brazil
IITomsk State Pedagogical University, 634041 Tomsk, Russia
IIILaboratory of Non-equilibrium State Theory, Institute of Strength Physics and Materials Science, 634021 Tomsk, Russia
ABSTRACT
The construction of q-local superfield Lagrangian BRST quantization in non-Abelian hypergauges for generic gauge theories based on the action principle is examined in the case of reducible local superfield models (LSM) on the basis of embedding a gauge theory into a special q-local superfield model with antisymplectic constraints and a Grassmann-odd time parameter q. We examine the problem of establishing a new correspondence between the odd-Lagrangian and odd-Hamiltonian formulations of a local LSM in the case of degeneracy of the Lagrangian description with respect to derivatives over q of generalized classical superfields AI(q). We also reveal the role of the nilpotent BRST-BFV charge for a formal dynamical system corresponding to the BV-BFV dual description of an LSM.
Keywords: Lagrangian (superfield) BV quantization; Odd Lagrangian and Hamiltonian formulations; Second-class constraints; Reducible multi-level non-Abelian hypergauges
I. INTRODUCTION
Local superfield Lagrangian BRST quantization [1] was originally proposed for irreducible gauge theories and Abelian hypergauges [2], which introduce the gauge-fixing procedure following the BV method [3], and then extended to arbitrary gauge models in reducible non-Abelian hypergauges of finite stage of reducibility [4]. The quantization rules [1] combine, in terms of superfields, a generalization of the "first-level" Batalin-Tyutin formalism [5] (the case of reducible hypergauges is examined in [6]) and a geometric realization of BRST transformations [7, 8] in the particular case of q-local superfield models (LSM) of Yang-Mills-type. The concept of an LSM [1, 2, 4], which realizes a trivial relation between the even t and odd q components of the object c = (t,q) called supertime [9], unlike the nontrivial interrelation realized by the operator D = ¶q + q¶t in the Hamiltonian superfield N = 1 formalism [10] of the BFV quantization [11], provides the basis for the method of local quantization [1, 2, 4] and proves to be fruitful in solving a number problems that restrict the applicability of the functional superfield Lagrangian method [12] to specific gauge theories. The idea of an LSM makes it possible to obtain an odd-Lagrangian and odd-Hamiltonian form of the classical master equation as a condition that preserves a q-local analogue of the energy by virtue of Noether's first theorem with respect to the evolution along the variable q, defined by superfield extensions of the extremals for an initial gauge model, i.e., by odd-Lagrangian (LS) and odd-Hamiltonian (HS) systems. The concept of an LSM provides an inclusion of the dual BV-BFV description [13, 14] of a reducible gauge theory in terms of a BRST charge for formal topological dynamical systems (i.e., systems without a definite time parameter) subject to first-class constraints of higher-stage reducibility in the problem of embedding a gauge algebra of a special reducible LSM into that of a general [25] LSM. Finally, the idea of an LSM proves to be an adequate extension of a usual gauge model in a superfield construction of the quantum action as a superfield analogue of the Koszul-Tate complex resolution [15, 16] in Lagrangian formalism on the basis of interpreting the reducibility relations as special gauge transformations of ghosts transformed into a unique q-integrable odd HS.
Along the lines of our previous works, we consider it an interesting task to solve two of the problems mentioned in the conclusion of the first paper of Ref. [1]. The first problem is that of establishing a different (from the one given by a Legendre transformation [1, 2, 4]) correspondence between the odd-Lagrangian and odd-Hamiltonian formulations of an LSM in the case of degeneracy of the Lagrangian description with respect to derivatives over q of generalized classical superfields
I(q), i.e.,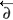 qI(q). The second problem is to reveal the role of the nilpotent BRST-BFV charge for a formal dynamical system corresponding to the BV-BFV dual description of an LSM.
qI(q). The second problem is to reveal the role of the nilpotent BRST-BFV charge for a formal dynamical system corresponding to the BV-BFV dual description of an LSM.
We devote this paper to the solution of the following problems:
1. A construction of an odd-Hamiltonian formulation for an LSM starting from an odd Lagrangian in the case of a degenerate Hessian supermatrix
I, ¶qJ) (q) on the basis of Dirac's algorithm in terms of a q-local antibracket.(q) of Refs. [1, 2, 4] as the supermatrix of second derivatives of the Lagrangian classical action, SL(q) = SL(
(q), ¶q
(q),q), with respect to odd velocities (¶q
2. An application of the BFV method [11] to a construction of formal counterparts of the BFV-BRST charge, gauge fermion and unitarizing Hamiltonian of a t-local field theory in terms of a q-local Dirac's antibracket, reflecting, in view of general gauge invariance, the presence of a subsystem of second-class constraints among all of the antisymplectic constraints.
3. Establishing a correspondence between the resulting odd-Hamiltonian formulation of an LSM with the BV quantum action for the gauge model corresponding to an LSM.
The paper is organized as follows. In Section 2, we apply Dirac's algorithm [17] to realize an odd Hamiltonization of a Lagrangian degenerate LSM, being an extension of a usual model of classical fields Ai, i = 1,...,n = n+ + n-, on a configuration space Mcl, to a q-local theory defined on an odd tangent bundle Todd
CLº PTCL = { I, ¶qI} , I = 1,...,N = N++N-, (n+,n-) < (N+,N-) with N+,(N-) bosonic (fermionic) superfields. The generalized classical superfields
I, ¶qI} , I = 1,...,N = N++N-, (n+,n-) < (N+,N-) with N+,(N-) bosonic (fermionic) superfields. The generalized classical superfields  I(q),
I(q),  I(q) = AI + lIq, parameterize the base
I(q) = AI + lIq, parameterize the base  CL (
CL ( clÌ
clÌ  CL) of the bundle PTCL and transform with respect to a J-superfield representation T of the direct product of supergroups
CL) of the bundle PTCL and transform with respect to a J-superfield representation T of the direct product of supergroups 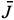 , P: J =
, P: J = 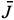 × P, P = exp(iµpq) [1, 2, 4], with
× P, P = exp(iµpq) [1, 2, 4], with 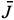 chosen as a spacetime SUSY group[26], and µ, pq being the respective nilpotent parameter and generator of q-shifts. The non-Lorentz [18] character of superfields
chosen as a spacetime SUSY group[26], and µ, pq being the respective nilpotent parameter and generator of q-shifts. The non-Lorentz [18] character of superfields  I(q) defined on
I(q) defined on  = {(zM, q)} = {zK} , zM Ì i Ì I, is reflected by a possible inclusion in their spectrum of additional (besides
= {(zM, q)} = {zK} , zM Ì i Ì I, is reflected by a possible inclusion in their spectrum of additional (besides  i(q)) superfields corresponding to the ghosts of the minimal sector in the BV quantization scheme [3]. In Section 3, following the BFV prescription, we construct q-local counterparts of the ghosts on the basis of a complete system of antisymplectic constraints and a Hamiltonian action SH0(q) defined on PT*
i(q)) superfields corresponding to the ghosts of the minimal sector in the BV quantization scheme [3]. In Section 3, following the BFV prescription, we construct q-local counterparts of the ghosts on the basis of a complete system of antisymplectic constraints and a Hamiltonian action SH0(q) defined on PT* CL =
CL = 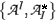 , a bosonic BRST charge SW(q), a unitarizing Hamiltonian action
, a bosonic BRST charge SW(q), a unitarizing Hamiltonian action 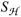 (q), and a gauge fermion FY(q). We specify to the case of a singular LSM a derivation of Lagrangian and Hamiltonian master equations from Noether's first theorem [19] applied to q-shifts, and establish a relation between the complete Hamiltonian action, SH(q) =
(q), and a gauge fermion FY(q). We specify to the case of a singular LSM a derivation of Lagrangian and Hamiltonian master equations from Noether's first theorem [19] applied to q-shifts, and establish a relation between the complete Hamiltonian action, SH(q) = 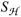 (q) + (SW(q), FY(q))qD, constructed via q-local Dirac's antibracket, and the quantum action of the BV method [3].
(q) + (SW(q), FY(q))qD, constructed via q-local Dirac's antibracket, and the quantum action of the BV method [3].
We mostly follow the conventions of Refs. [1, 4] based on DeWitt's condensed notation [20] and distinguish between two types of superfield derivatives: the right (left) derivative
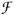 (q)/¶Gp(q) (
(q)/¶Gp(q) (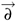
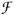 (q)/¶Gp(q)) of a function
(q)/¶Gp(q)) of a function 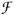 (q) for a fixed q, and the right (left) variational derivative
(q) for a fixed q, and the right (left) variational derivative 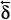 F/dFA(q) (
F/dFA(q) (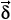 F/dFA(q)) of a functional F. In the same manner, superfield right (left) covariant derivatives with respect to a superfield Gp(q) are denoted by
F/dFA(q)) of a functional F. In the same manner, superfield right (left) covariant derivatives with respect to a superfield Gp(q) are denoted by 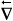 p(q)F (
p(q)F (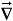 p(q)F) for a fixed q, and variational derivatives are denoted by
p(q)F) for a fixed q, and variational derivatives are denoted by 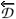 p(q)F (
p(q)F (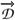 p(q)F). Derivatives with respect to super(anti)fields and their components are understood as acting from the right (left), for instance,
p(q)F). Derivatives with respect to super(anti)fields and their components are understood as acting from the right (left), for instance, 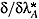 or d/dFA(q); in the opposite case we use arrows "®" ("¬") for left (right) differentiation. For right-hand derivatives with respect to
or d/dFA(q); in the opposite case we use arrows "®" ("¬") for left (right) differentiation. For right-hand derivatives with respect to  I(q) for a fixed q, we use the notation
I(q) for a fixed q, we use the notation 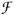 ,I(q) º ¶
,I(q) º ¶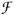 (q)/¶
(q)/¶ I(q). As in [1, 4], following the definitions of Refs. [21, 22], a smooth supersurface [27]S, is parameterized by local coordinates zi(q), and the rank of an even q-local supermatrix ||G(q)|| with Z2-grading e is characterized by a pair of numbers
I(q). As in [1, 4], following the definitions of Refs. [21, 22], a smooth supersurface [27]S, is parameterized by local coordinates zi(q), and the rank of an even q-local supermatrix ||G(q)|| with Z2-grading e is characterized by a pair of numbers 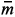 = (m+, m-): rank||G(q)|| = rank||G(0)||, dimS = dimS|q = 0 with S| q = 0 parameterized by zi(0). We characterize the property of a quantity F to be bosonic or fermionic by a triplet of Z2-gradings,
= (m+, m-): rank||G(q)|| = rank||G(0)||, dimS = dimS|q = 0 with S| q = 0 parameterized by zi(0). We characterize the property of a quantity F to be bosonic or fermionic by a triplet of Z2-gradings, 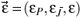 , so that the basic Grassmann parity e, according to [1, 2, 4], is given by the sum,
, so that the basic Grassmann parity e, according to [1, 2, 4], is given by the sum,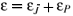 , of Z2-gradings
, of Z2-gradings 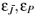 , being the Grassmann parities of coordinates of the corresponding representation spaces of supergroups
, being the Grassmann parities of coordinates of the corresponding representation spaces of supergroups 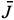 , P.
, P.
II. CLASSICAL FORMULATION OF A DEGENERATE q-LOCAL SUPERFIELD MODEL
In order to provide an equivalent description of a general LSM degenerate with respect to superfields ( ¶q )I(q) in odd-Lagrangian and odd-Hamiltonian formulations, we consider a procedure of the odd Hamiltonization of a Lagrangian LSM that preserves
)I(q) in odd-Lagrangian and odd-Hamiltonian formulations, we consider a procedure of the odd Hamiltonization of a Lagrangian LSM that preserves 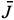 -covariance. Using these results, in the next section we will apply the BFV-BRST approach in order to construct from the odd Hamiltonian formulation of an LSM a complete Hamiltonian action SH(q) and extend the BV-BFV dual description inherent in the q-local approach to the case of a degenerate LSM. We will also establish a relation with the quantum action of the BV method for the physical gauge model contained in an LSM.
-covariance. Using these results, in the next section we will apply the BFV-BRST approach in order to construct from the odd Hamiltonian formulation of an LSM a complete Hamiltonian action SH(q) and extend the BV-BFV dual description inherent in the q-local approach to the case of a degenerate LSM. We will also establish a relation with the quantum action of the BV method for the physical gauge model contained in an LSM.
2.1 Odd-Lagrangian Formulation
Let us recall that the Lagrangian formulation (based on the variational principle) of an Lg-stage reducible LSM of generalized classical superfields  , is defined by a Lagrangian action SL, PT
, is defined by a Lagrangian action SL, PT
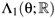 , being a C¥(PTCL)-function taking its values in a real Grassmann algebra
, being a C¥(PTCL)-function taking its values in a real Grassmann algebra 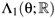 , and (independently) by a functional ZL[
, and (independently) by a functional ZL[ ], whose q-density is defined with accuracy up to an arbitrary
], whose q-density is defined with accuracy up to an arbitrary 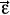 -bosonic function f((
-bosonic function f(( , ¶q
, ¶q )(q),q) Î ker{¶q},
)(q),q) Î ker{¶q},
invariant with respect to general gauge transformations,
with a superfield Euler-Lagrange derivative  that determines LSM dynamics and (on the assumption of locality and
that determines LSM dynamics and (on the assumption of locality and 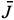 -covariance) with functionally dependent generators
-covariance) with functionally dependent generators  (q; q0)
(q; q0)
The dependence of  implies an existence (on solutions of the odd LS (2.3)) of proper zero-eigenvalue eigenvectors,
implies an existence (on solutions of the odd LS (2.3)) of proper zero-eigenvalue eigenvectors,  , with a structure similar to
, with a structure similar to  in (2.4), which exhaust the zero-modes of the generators and are dependent in case rank
in (2.4), which exhaust the zero-modes of the generators and are dependent in case rank  . Thus, a general Lg-reducible LSM is defined by the reducibility relations, for s = 1,...,Lg,
. Thus, a general Lg-reducible LSM is defined by the reducibility relations, for s = 1,...,Lg,  s = 1,..., Ms = Ms++Ms-,
s = 1,..., Ms = Ms++Ms-,
For Lg = 0, the LSM is an irreducible general gauge theory.
Due to the J-scalar nature of ZL[ ] it is only SL(q), among the objects SL(q) and ZL[
] it is only SL(q), among the objects SL(q) and ZL[ ] invariant under the action of a J-superfield representation T restricted to
] invariant under the action of a J-superfield representation T restricted to  , that transforms nontrivially with respect to the total representation T under
, that transforms nontrivially with respect to the total representation T under 
Eq. (2.6) is written [1, 2, 4] in terms of the nilpotent operator (¶qU)(q) = ¶q
I(q)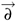 /¶
/¶ I(q) = [¶q,U(q)]-, U(q) = P1I(q)
I(q) = [¶q,U(q)]-, U(q) = P1I(q)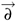 /¶
/¶ I(q), by means of projectors onto C¥(PT(*)CL) × {q}: {Pa(q) = da0(1 - q¶q) + da1q¶q, a = 0,1}. The superfield Euler-Lagrange equations (2.3) are equivalent (in view of
I(q), by means of projectors onto C¥(PT(*)CL) × {q}: {Pa(q) = da0(1 - q¶q) + da1q¶q, a = 0,1}. The superfield Euler-Lagrange equations (2.3) are equivalent (in view of 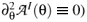 to an odd LS characterized by 2N formally second-order differential equations in q,
to an odd LS characterized by 2N formally second-order differential equations in q,


so that the subset of formal equations (2.7) does not affect LSM dynamics, in particular, identities (2.2) and relations (2.5); however, it determines, depending on the (non)degeneracy of the supermatrix  , a possibility of presenting LS (2.3) in the normal form. The Lagrangian constraints (2.8), QI(q) = QI((
, a possibility of presenting LS (2.3) in the normal form. The Lagrangian constraints (2.8), QI(q) = QI(( ,¶q
,¶q )(q),q) are functionally dependent as first-order equations in q, restricting the setting of the Cauchy problem for the LS, and thus determine the general gauge algebra of an LSM by Eqs. (2.2)-(2.5).
)(q),q) are functionally dependent as first-order equations in q, restricting the setting of the Cauchy problem for the LS, and thus determine the general gauge algebra of an LSM by Eqs. (2.2)-(2.5).
For an LSM which enables one to represent SL(q) in the form of a natural system in usual classical mechanics, SL(q) = T( ¶q (q)) - S(
(q)) - S( (q),q) , the functions QI(q), QI(q) Î C¥(
(q),q) , the functions QI(q), QI(q) Î C¥( CL×{q}) are given by the relations
CL×{q}) are given by the relations
being, for q = 0, the extremals of the functional S0(A) = S( (0),0) , S0(A) Î C¥(MCL) , MCL =
(0),0) , S0(A) Î C¥(MCL) , MCL =  CL|q = 0. Relations (2.2) and (2.5) assume the standard (in case q = 0) form of the relations of a special gauge algebra with linearly dependent generators
CL|q = 0. Relations (2.2) and (2.5) assume the standard (in case q = 0) form of the relations of a special gauge algebra with linearly dependent generators  of special gauge transformations,
of special gauge transformations,  , that leave invariant only S(q), in contrast to T(q),
, that leave invariant only S(q), in contrast to T(q),
in the rank conditions for the special zero-eigenvalue eigenvectors 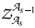 (q):
(q):
In case rank  an LSM defined by relations (2.10), (2.11) is called a special gauge theory of Lg-stage reducibility.
an LSM defined by relations (2.10), (2.11) is called a special gauge theory of Lg-stage reducibility.
The special gauge algebra of this LSM is q-locally embedded into the gauge algebra of a general gauge theory with the functional ZL[ ] = (¶qT-S)(q), which leads to a relation between the eigenvectors,
] = (¶qT-S)(q), which leads to a relation between the eigenvectors,
and to a possible parametric dependence of the structure functions of a special gauge theory on ¶q
I(q) . As noted in [1, 4], an extended (in comparison with {Pa(q) }, a = 0,1) system of projectors onto C¥(PTCL × {q}), {P0(q),q¶/¶q,U(q)}, selects in (2.10), (2.11) two kinds of gauge algebra: one is selected by means of the subsystem {P0(q),U(q)}, with the corresponding structure equations and functions [S,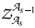 ](
]( (q)) not depending explicitly on q, and another with the help of P0(q) with the standard (in case q = 0, (eP)I =
(q)) not depending explicitly on q, and another with the help of P0(q) with the standard (in case q = 0, (eP)I = 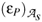 = 0, s = 1,...,Lg) relations for the gauge algebra of a reducible model with quantities
= 0, s = 1,...,Lg) relations for the gauge algebra of a reducible model with quantities 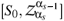 (A) under the assumption of the completeness of reduced generators and eigenvectors
(A) under the assumption of the completeness of reduced generators and eigenvectors 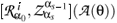 .
.
As shown in Refs. [1, 2, 4], a characteristic feature of the q-local extension of a usual field theory to an LSM is the application of Noether's first theorem [19] to provide the invariance of the density dqSL(q) under global q-translations as symmetry transformations of the superfields  I(q) and coordinates (zM,q), (
I(q) and coordinates (zM,q), ( I,zM,q) ® (
I,zM,q) ® ( I, zM,q + µ). It is easy to see that the function
I, zM,q + µ). It is easy to see that the function
is an LS integral of motion, namely, a quantity preserved by q-evolution, assuming the fulfillment of the generalized Lagrangian master equation
Eq. (2.15) follows from the principle of dynamical symmetry in contrast to the standard (Hamiltonian-like) master equation in the minimal sector of the BV method [3] which is based on differential-algebraic reasons as a generating equation encoding the standard relations of the gauge algebra and the structure functions 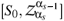 (A). The function SE(q) may also be an LS integral in the case of an explicit dependence on q, unlike its analogue in a t-local field theory, the energy E(t), in case SL(q) admits the representation
(A). The function SE(q) may also be an LS integral in the case of an explicit dependence on q, unlike its analogue in a t-local field theory, the energy E(t), in case SL(q) admits the representation
If SL(q) does not depend on q explicitly,  Eq. (2.15) transforms into a Lagrangian master equation,
Eq. (2.15) transforms into a Lagrangian master equation,  . As was announced in Ref. [2], a sufficient condition for the existence of a proper solution
. As was announced in Ref. [2], a sufficient condition for the existence of a proper solution  L(q) for the Lagrangian master equation is the presence of an independent special Lagrangian constraints for a certain division of the index I,
L(q) for the Lagrangian master equation is the presence of an independent special Lagrangian constraints for a certain division of the index I,
2.2 Odd Hamiltonization
A possibility of presenting the odd LS (2.3) in the normal form (which, in a t-local field theory, provides a basis for the generalized canonical quantization of a given dynamical system) depends on the existence of an inverse for the supermatrix  in (2.7).
in (2.7).
2.2.1 Nondegenerate Case
In this case, the LSM is reformulated in the odd-Hamiltonian description [1, 2, 4] on the odd phase space PT* CL =
CL =  =
=  (q)} in terms of a Hamiltonian action being a C¥(PT*
(q)} in terms of a Hamiltonian action being a C¥(PT* CL)-function, SH: PT*
CL)-function, SH: PT* CL× {q} ® L1(q;
CL× {q} ® L1(q; ), constructed from the Lagrangian formulation through a Legendre transformation of SL(q) with respect to
), constructed from the Lagrangian formulation through a Legendre transformation of SL(q) with respect to  q
q
The action SH(q) coincides with SE(q) in terms of the PT* CL-coordinates.
CL-coordinates.
An odd HS equivalent to the LS follows from (2.3) due to transformations (2.18) and is implied by the condition of the existence of a critical superfield configuration for a fermionic functional ZH[GCL] identical to ZL[ ],
],
it is written in the square brackets in Eq. (2.20) with the help of a q-local antibracket and an antisymplectic potential, VP(Gk(q)) = 1/2 (q), defined with respect to an odd Poisson bivector
(q), defined with respect to an odd Poisson bivector  and a flat antisymplectic metric
and a flat antisymplectic metric  antidiag
antidiag  .
.
The equivalence of HS (2.20) and LS (2.7), (2.8) is provided by the fact that the Lagrangian constraints QI(q) transformed into the Hamiltonian constraints  in terms of the PT*
in terms of the PT* CL-coordinates coincide with half of the HS equations due to transformations (2.18) and their consequences:
CL-coordinates coincide with half of the HS equations due to transformations (2.18) and their consequences:
The equivalence between the LS and HS is guaranteed by the corresponding [formal, in view of the degeneracy conditions (2.2)] setting of the Cauchy problem (q = 0, k = CL) for integral curves  modulo the continuous part of I,
modulo the continuous part of I,
The definition of a special gauge algebra (2.10), (2.11) remains the same in the Hamiltonian formulation, whereas the definition (2.2), (2.3) of a general Lg-stage reducible LSM is transformed by the rule
The fulfillment of the generalized Lagrangian master equation (2.15) for SL(q) implies, in view of definition (2.14), transformations (2.18) and their consequence,  that the Hamiltonian action is an HS integral of motion (i.e., a quantity invariant under q-shifts along arbitrary solutions
that the Hamiltonian action is an HS integral of motion (i.e., a quantity invariant under q-shifts along arbitrary solutions  by (eP, e)-odd µ) due to a generalized Hamiltonian master equation,
by (eP, e)-odd µ) due to a generalized Hamiltonian master equation,
The equation Qcompl(q)SH(q) = 0, written in terms of an odd operator Qcompl(q), holds true also in the case of an explicit dependence of SH(q) on q, according to (2.16),
where  is a Legendre transform of
is a Legendre transform of  , and
, and  If SH(q) does not depend on q explicitly, (¶/¶q)SH(q) = 0; then Eq. (2.25) transforms into the Hamiltonian master equation (SH(q), SH(q)) q = 0. This imposes the condition [3] for SH(q) to be proper, which has no counterpart in a t-local field theory. Sufficient conditions of the solvability of the latter equation is the presence of irreducible special Hamiltonian constraints ja(Gk(q)) [2], equivalent to the constraints (2.17), being of first-class with respect to the antibracket:
If SH(q) does not depend on q explicitly, (¶/¶q)SH(q) = 0; then Eq. (2.25) transforms into the Hamiltonian master equation (SH(q), SH(q)) q = 0. This imposes the condition [3] for SH(q) to be proper, which has no counterpart in a t-local field theory. Sufficient conditions of the solvability of the latter equation is the presence of irreducible special Hamiltonian constraints ja(Gk(q)) [2], equivalent to the constraints (2.17), being of first-class with respect to the antibracket:
As a consequence, the q-superfield integrability of HS (2.20) is guaranteed by the properties of the antibracket, including the Jacobi identity
and the q-translation formula written in terms of a nilpotent BRST-like generator  of q-shifts along an (ep,e)-odd vector field Q(q) º adSH(q) = (SH(q), ·)q, acting on C¥(PT*
of q-shifts along an (ep,e)-odd vector field Q(q) º adSH(q) = (SH(q), ·)q, acting on C¥(PT* CL×{q}), namely,
CL×{q}), namely,
Following Refs. [1, 2, 4] and depending on the realization of additional properties of a gauge theory, we assume the fulfillment of the equation
for a trivial (in the case of a flat odd phase-space) choice of the density function r(G(q)), r = 1, which is equivalent to a vanishing antisymplectic divergence of Q(q),  .
.
2.2.2 Degenerate Case
The degeneracy of  implies the impossibility of applying the above procedure of odd Hamiltonization and requires the use of an odd counterpart of Dirac's algorithm in order to reduce the odd LS (2.3) to a normal form (with only
implies the impossibility of applying the above procedure of odd Hamiltonization and requires the use of an odd counterpart of Dirac's algorithm in order to reduce the odd LS (2.3) to a normal form (with only 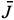 -covariance preservation). Let the degree of degeneracy of
-covariance preservation). Let the degree of degeneracy of  be given by the relation
be given by the relation
valid almost everywhere in PTCL. It means the impossibility to express each 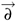 q
q
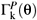 using equations
using equations 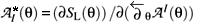 in (2.18), which is equivalent to a functional dependence among the antifields
in (2.18), which is equivalent to a functional dependence among the antifields 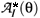 in the form of primary antisymplectic constraints,
in the form of primary antisymplectic constraints,
In view of the preservation of 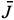 -covariance, the constraints
-covariance, the constraints  may be dependent for
may be dependent for  and assuming the existence of an analog of the regularity conditions [16], these constraints define a (2
and assuming the existence of an analog of the regularity conditions [16], these constraints define a (2 -
- -1)-dimensional submanifold smoothly embedded in
-1)-dimensional submanifold smoothly embedded in  . The above regularity conditions imply the existence of an open covering of the constraints surface,
. The above regularity conditions imply the existence of an open covering of the constraints surface,  = 0, by open regions on each of which there exists a local separation of constraints:
= 0, by open regions on each of which there exists a local separation of constraints:
where A0 = (A'0,a'0)  .
.
For an LSM with primary constraints, there hold the following statements:
Theorem 1 For any C¥(PT*
CL)-function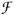 (GCL(q),q) vanishing on the constraint surface,
(GCL(q),q) vanishing on the constraint surface, 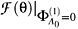 = 0, there exist functions
= 0, there exist functions 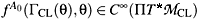 such that
such that 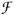 (q) is a linear combination of constraints:
(q) is a linear combination of constraints: 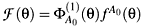 .
.
Theorem 2 Due to the solution of the equation LP(GCL(q),q) = 0 for arbitrary variations
= 0 for arbitrary variations  , the functions
, the functions
are tangent to the constraints surface.
A sketch of a proof: the validity of Theorem 1 follows from the partition of unity on PT* CL and from the fact that from the local validity of representation (2.33) follows the existence of an invertible change of variables,
CL and from the fact that from the local validity of representation (2.33) follows the existence of an invertible change of variables,  (Gk(q)), M0 = 1,...,2N - R-1, so that
(Gk(q)), M0 = 1,...,2N - R-1, so that  = 0. Therefore, in a regular coordinate system
= 0. Therefore, in a regular coordinate system  one has
one has
The validity of Theorem 2 follows from the fact that the variations  tangent to the surface
tangent to the surface 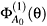 = 0 at a certain point form a (2
= 0 at a certain point form a (2 -
-  -1)-dimensional superspace so that there exist R-1 independent solutions of
-1)-dimensional superspace so that there exist R-1 independent solutions of  = 0. By virtue of the regularity conditions (2.33), the above solutions may be chosen as a linear combination (2.34) of the antisymplectic gradients,
= 0. By virtue of the regularity conditions (2.33), the above solutions may be chosen as a linear combination (2.34) of the antisymplectic gradients,  (q), with functions
(q), with functions  unambiguously defined for
unambiguously defined for  .
.
The Hamiltonian action SH(Gk(q),q) in (2.18) is well-defined as a Legendre transformation of SL(q) only on the surface  The definition of the Hamiltonian action by the rule (2.18) on the entire PT*
The definition of the Hamiltonian action by the rule (2.18) on the entire PT* k is possible due to an extension of SH(q) by the addition of linear combination of constraints:
k is possible due to an extension of SH(q) by the addition of linear combination of constraints:
Actually, Eqs. (2.18) implies the following equations under a variation on the constraints surface:
which, in accordance with Theorem 2, admit the solution
In the case of independent constraints, the unknown functions  can be uniquely obtained from the first equations for
can be uniquely obtained from the first equations for 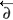 q
q
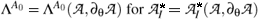 in contrast to dependent
in contrast to dependent 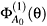 .
.
The invertible Legendre transformation, corresponding to Eqs. (2.36), of SL(q) from PT
CL to the surface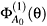 = 0 of THE bundle
= 0 of THE bundle 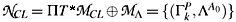 and its inverse are given by the relations
and its inverse are given by the relations
We assume that the local consideration of the Legendre transformation made in Eqs. (2.36)-(2.38) holds globally.
The corresponding odd HS equivalent to LS (2.3) is implied by relations (2.18), (2.35)-(2.38) following from the variational principle for a fermionic functional  extended, as compared with ZH[Gk] in (2.19), by means of linear combinations of the constraints
extended, as compared with ZH[Gk] in (2.19), by means of linear combinations of the constraints 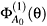 with superfields
with superfields  as Lagrangian multipliers,
as Lagrangian multipliers,
A relation between the Cauchy problem (or the boundary problem) for an LS and HS should be specified in view of 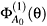 , whereas the restriction of the action
, whereas the restriction of the action  remains an expression of the function SE(q) in terms of PT*
remains an expression of the function SE(q) in terms of PT* CL-coordinates.
CL-coordinates.
By the Legendre transformation, the consequence (2.37) is a change of SH,I(q) by  (q) in expression (2.21) for the Hamiltonian constraints
(q) in expression (2.21) for the Hamiltonian constraints  , preserving the equivalence of a generalized HS that consists of the constraints
, preserving the equivalence of a generalized HS that consists of the constraints  H(q) and HS (2.40) itself. In this case, the definition of the gauge algebra (2.23) in case of a nondegenerate supermatrix
H(q) and HS (2.40) itself. In this case, the definition of the gauge algebra (2.23) in case of a nondegenerate supermatrix  is not affected by the change
is not affected by the change  by virtue of the identities dZH/d
by virtue of the identities dZH/d I(q) =
I(q) =  implied by Eqs. (2.37).
implied by Eqs. (2.37).
Locally, having assumed that condition (2.31) is fulfilled in a vicinity of the configurations  = (0,0) the structure of the primary constraints
= (0,0) the structure of the primary constraints  can be specified. Now, as the regularity conditions (2.33), one can assume, while neglecting
can be specified. Now, as the regularity conditions (2.33), one can assume, while neglecting 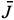 -covariance, that there exists a separation of the superfields
-covariance, that there exists a separation of the superfields  compatible with (2.31),
compatible with (2.31),
In this case, the action  depends neither on the antifields
depends neither on the antifields  nor on the primary non-expressible superfields
nor on the primary non-expressible superfields 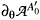 due to the direct Legendre transformation (2.37), in which, instead of
due to the direct Legendre transformation (2.37), in which, instead of  , one writes
, one writes 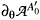 , and due to the fact that the action SL(q) is at most homogeneous of degree 1 with respect to
, and due to the fact that the action SL(q) is at most homogeneous of degree 1 with respect to 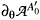 . The action
. The action  ((Gk,L)(q),q) has the form
((Gk,L)(q),q) has the form
where the odd velocities ¶q
I0(q) are resolved from the relations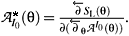 . In turn, Eqs. (2.38) imply the coincidence of the Lagrangian multipliers
. In turn, Eqs. (2.38) imply the coincidence of the Lagrangian multipliers 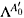 and
and 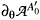 .
.
Having obtained an equivalent description of the LSM in terms of the Hamiltonian action  , and following the q-local analog of Dirac's algorithm, we need to check the compatibility of the odd HS in (2.40), being the preservation of the constraints by the q-evolution generated by the vector field
, and following the q-local analog of Dirac's algorithm, we need to check the compatibility of the odd HS in (2.40), being the preservation of the constraints by the q-evolution generated by the vector field  ,
,
Eqs. (2.43) may contain a subsystem with  equations independent from
equations independent from  with residual
with residual  equations permitting to find a part of
equations permitting to find a part of  as functions of
as functions of 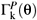 if
if  . In the former case, if a subsystem of
. In the former case, if a subsystem of  equations does not depend on
equations does not depend on 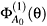 , i.e., if there exists a set
, i.e., if there exists a set  of {
of {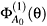 } such that
} such that
The above expression defines dependent (in general) secondary antisymplectic constraints  Î C¥(PT*
Î C¥(PT* k),
k),
The constraints  , in contrast to
, in contrast to 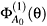 , are not valid identically in the entire PT*
, are not valid identically in the entire PT* k, but only on solutions of the odd HS (2.40).
k, but only on solutions of the odd HS (2.40).
The consistency conditions for the secondary constraints  of the form (2.43),
of the form (2.43),  lead to new (generally dependent) secondary antisymplectic constraints,
lead to new (generally dependent) secondary antisymplectic constraints,  =
=  (q) = 0, A2 = 1,...,
(q) = 0, A2 = 1,...,  =
=  among
among  equations not containing
equations not containing  in the relations for the subset
in the relations for the subset  ,
,
The remaining part of  equations in
equations in  permits one to define, in the case of
permits one to define, in the case of  a part of the superfields
a part of the superfields  as functions of
as functions of 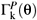 . A proof of consistency conditions for the constraints
. A proof of consistency conditions for the constraints  permits one to obtain new secondary antisymplectic constraints
permits one to obtain new secondary antisymplectic constraints  and a part from
and a part from  , etc.
, etc.
As a result of this algorithm, the complete set of
0 dependent antisymplectic constraints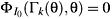 consisting of the primary
consisting of the primary 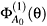 and the remaining
and the remaining 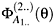 , called secondary ones, is defined as
, called secondary ones, is defined as
From the nonhomogeneous linear equations with unknowns  (q), whose number is
(q), whose number is  ,
,
with the symbol "»" for a weak equality in view of Theorem 1,  the consistency of Dirac's algorithm implies the existence of a general solution in the form
the consistency of Dirac's algorithm implies the existence of a general solution in the form
Here,  is a particular solution of the nonhomogeneous equations and the functions
is a particular solution of the nonhomogeneous equations and the functions  define linearly independent solutions of homogeneous equations associated to (2.46), with
define linearly independent solutions of homogeneous equations associated to (2.46), with  const[28]. The coefficients
const[28]. The coefficients  in Eqs. (2.47) are arbitrary.
in Eqs. (2.47) are arbitrary.
Relations (2.47) allow one to rewrite HS (2.40) in terms of a total Hamiltonian action  ,
,
with  =
=  and linearly dependent constraints
and linearly dependent constraints  and proper zero-eigenvalue eigenvectors,
and proper zero-eigenvalue eigenvectors,  for a rigorous inequality being dependent as well.
for a rigorous inequality being dependent as well.
Following Dirac's terminology, the concept of (q-local) quantities of first and second classes is defined by the fact that an arbitrary C¥(PT* k)-function
k)-function 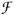 (Gk(q),q) either obeys the relations
(Gk(q),q) either obeys the relations
(and is said to be a first-class function) or is a second-class one if it does not obey Eqs. (2.49). Jacobi's identity for the antibracket (·,·)q implies that the set of first-class functions forms a Lie algebra  I with a multiplication with respect to the antibracket, i.e., for any
I with a multiplication with respect to the antibracket, i.e., for any  (q),
(q), (q) Î
(q) Î  I, (
I, (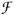 (q),
(q),  (q))q Î
(q))q Î  I. By definition, it follows that the total action
I. By definition, it follows that the total action  is the sum of certain quantities
is the sum of certain quantities 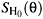 and
and  in view of the non-uniqueness of the particular solution
in view of the non-uniqueness of the particular solution  of Eqs. (2.46) which are given by the gauge algebra of reducible antisymplectic primary first-class constraints
of Eqs. (2.46) which are given by the gauge algebra of reducible antisymplectic primary first-class constraints  :
:
with 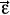 -odd quantities (U, V) and
-odd quantities (U, V) and 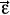 -even
-even  .
.
The primary constraints 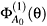 may be related with the reducible antisymplectic gauge transformations,
may be related with the reducible antisymplectic gauge transformations,  in C¥(PT*
in C¥(PT* k) (different from general gauge transformations,
k) (different from general gauge transformations,  which correspond to the difference between the values of
which correspond to the difference between the values of 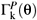 at q and at (q + µ) under two different choices of the Lagrangian multipliers
at q and at (q + µ) under two different choices of the Lagrangian multipliers  :
:  with arbitrary functions
with arbitrary functions  (q) on
(q) on  ,
,
For the choice  with arbitrary functions
with arbitrary functions  (q) on
(q) on  , being the Grassmann parities
, being the Grassmann parities  + (1,0,1) if
+ (1,0,1) if  , the above transformations vanish on the constraint surface,
, the above transformations vanish on the constraint surface,  .
.
The functional  , given by
, given by
is invariant not only with respect to the transformations  , in view of the relation ZH =
, in view of the relation ZH =  and Eqs. (2.23), but also with respect to extended antisymplectic transformations in C¥(PT*
and Eqs. (2.23), but also with respect to extended antisymplectic transformations in C¥(PT* CL Å
CL Å  l),
l),
Following an analog of "Dirac's conjecture" in the usual Hamiltonian treatment of a gauge model, one may suggest that the structure of SL(q) for an LSM be such that secondary first-class antisymplectic constraints are generators of antisymplectic gauge transformations as well.
A characteristic feature of odd Hamiltonization is the possibility of an explicit identification of so-called antisymplectic gauge freedom in comparison with the odd-Lagrangian formulation of an LSM which is related to the construction of an extended Hamiltonian action  and a functional
and a functional  , including all the constraints
, including all the constraints  ,
,
The variational principle for  encodes an HS, which is not entirely equivalent to LS (2.3),
encodes an HS, which is not entirely equivalent to LS (2.3),
The system of antisymplectic constraints { (q)} contains two subsystems {
(q)} contains two subsystems { } =
} =  of first-class
of first-class  and second-class
and second-class  constraints extracted from the initial system by means of certain quantities
constraints extracted from the initial system by means of certain quantities  =
=  so that only the functions
so that only the functions  from the set of Lagrangian multipliers
from the set of Lagrangian multipliers  =
=  , remain completely undetermined by the evolution of HS (2.54).
, remain completely undetermined by the evolution of HS (2.54).
By definition, we consider that an  -stage reducible system of antisymplectic constraints
-stage reducible system of antisymplectic constraints  (q) =
(q) =  (q) is divided to a subsystem of
(q) is divided to a subsystem of  -stage reducible first-class constraints
-stage reducible first-class constraints  and that of
and that of  -stage reducible second-class ones
-stage reducible second-class ones  if
if
where  and
and
where we have used the standard distribution [1, 3] of ghost number in PT* CL.
CL.
A complete definition of the subsystem of second-class antisymplectic constraints  may be obtained directly from Eqs. (2.57) under the change
may be obtained directly from Eqs. (2.57) under the change  . For
. For  = 0 (
= 0 ( = 0), the subsystem
= 0), the subsystem 
 , is referred to as irreducible first-class (second-class) antisymplectic constraints. The definitions in Eqs. (2.55)-(2.58) generalize, to the case of reducible mixed antisymplectic constraints in the context of a dynamical LSM, the formal definition [6, 23] of irreducible second-class antisymplectic constraints for q = 0 .
, is referred to as irreducible first-class (second-class) antisymplectic constraints. The definitions in Eqs. (2.55)-(2.58) generalize, to the case of reducible mixed antisymplectic constraints in the context of a dynamical LSM, the formal definition [6, 23] of irreducible second-class antisymplectic constraints for q = 0 .
The presence of the reducible constraints { } permits one to construct a so-called weak Dirac's antibracket possessing all the properties of the odd Poisson bracket on the constraint surface
} permits one to construct a so-called weak Dirac's antibracket possessing all the properties of the odd Poisson bracket on the constraint surface  = 0 by means of a degenerate odd Poisson-Dirac bivector:
= 0 by means of a degenerate odd Poisson-Dirac bivector:
with the quantities  determined on the surface
determined on the surface  for any
for any  characterizing the Dirac antibracket, by the equations
characterizing the Dirac antibracket, by the equations
The functions  in (2.60) may be specified due to the consequence
in (2.60) may be specified due to the consequence  of relations (2.56), (2.58), applied to the constraints
of relations (2.56), (2.58), applied to the constraints  in the form
in the form  .
.
The fact that Dirac's antibracket obeys the generalized Jacobi identity in the entire PT* k or on the surface
k or on the surface  = 0 can be extended according to the construction of a weak even Dirac bracket for infinitely reducible second-class symplectic constraints [24] used to quantize the N = 1 Brink-Schwarz superparticle and the N = 1, d = 9 massive superparticle with the Wess-Zumino term.
= 0 can be extended according to the construction of a weak even Dirac bracket for infinitely reducible second-class symplectic constraints [24] used to quantize the N = 1 Brink-Schwarz superparticle and the N = 1, d = 9 massive superparticle with the Wess-Zumino term.
As in the case of the initial antibracket, there exists an odd weak nilpotent (on  = 0) Laplacian
= 0) Laplacian  , corresponding to antibracket (·,·)qD, such that Dirac's antibracket weakly equals to the failure of
, corresponding to antibracket (·,·)qD, such that Dirac's antibracket weakly equals to the failure of  to act as a derivative on the product of two functions in C¥(PT*
to act as a derivative on the product of two functions in C¥(PT* k),
k),
with an 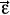 -even density function rD(Gk(q)). The operator
-even density function rD(Gk(q)). The operator  generalizes the properties of its analogue for irreducible antisymplectic second-class constraints in Ref. [6], for
generalizes the properties of its analogue for irreducible antisymplectic second-class constraints in Ref. [6], for  in Eqs. (2.56).
in Eqs. (2.56).
From the definition of Dirac's antibracket and relations (2.56)-(2.59), there follows, for any first-class C¥(PT* k)-functions [
k)-functions [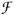 ,
,  ](q) and arbitrary C¥(PT*
](q) and arbitrary C¥(PT* k)-function
k)-function  (q), the validity of the weak equalities
(q), the validity of the weak equalities
By virtue of the fact that  is a first-class quantity, the Dirac antibracket generates the odd HS (2.54), where it is possible to change the antibracket (·,·)q by (·,·)qD. In turn, the definition of the first-class constraint subsystem (2.55), with allowance for relations (ref2.61), may be rewritten in terms of Dirac's antibracket with a weak equality which means an equality modulo
is a first-class quantity, the Dirac antibracket generates the odd HS (2.54), where it is possible to change the antibracket (·,·)q by (·,·)qD. In turn, the definition of the first-class constraint subsystem (2.55), with allowance for relations (ref2.61), may be rewritten in terms of Dirac's antibracket with a weak equality which means an equality modulo  . Note that in view of the inequality
. Note that in view of the inequality  the functional
the functional  is not invariant under the general gauge transformations
is not invariant under the general gauge transformations  due to the presence of the secondary constraints
due to the presence of the secondary constraints  .
.
III. ODD-LAGRANGIAN FORM OF BFV-BRST METHOD APPLICATION TO ODD-HAMILTONIAN LSM
Let us apply the BFV-BRST method [11] to an LSM in the odd Hamiltonian formulation which has been made more complex by the presence of the  -reducible first- and second-class antisymplectic constraints. The construction of an analog SW(q) of the BFV-BRST charge, encoding, in terms of Dirac's antibracket, the gauge algebra structure functions of the antisymplectic first-class constraints
-reducible first- and second-class antisymplectic constraints. The construction of an analog SW(q) of the BFV-BRST charge, encoding, in terms of Dirac's antibracket, the gauge algebra structure functions of the antisymplectic first-class constraints  and the eigenvectors
and the eigenvectors  , as well as the enhanced antisymplectic gauge transformations, can be described by a superfield algorithm similar to the construction of the superfield BV action in Refs. [1, 4]. Let us consider the gauge transformations (2.52) restricted in the minimal sector of superfields
, as well as the enhanced antisymplectic gauge transformations, can be described by a superfield algorithm similar to the construction of the superfield BV action in Refs. [1, 4]. Let us consider the gauge transformations (2.52) restricted in the minimal sector of superfields  for all first-class constraints
for all first-class constraints  ,
,
which, due to the definition  and the substitution, instead of arbitrary
and the substitution, instead of arbitrary  , of the ghosts
, of the ghosts  , are embedded into the odd HS in PT*
, are embedded into the odd HS in PT* k with 2N equations (for µ = dq)
k with 2N equations (for µ = dq)
In view of (2.58), the function  is invariant, modulo
is invariant, modulo  , with respect to antisymplectic gauge transformations of ghosts
, with respect to antisymplectic gauge transformations of ghosts  , with arbitrary functions
, with arbitrary functions  Î C¥
Î C¥ , (
, (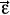 ,gh)
,gh)  ,
,
Making the substitution  and extending
and extending  first-order equations in q with respect to unknown
first-order equations in q with respect to unknown  in transformations (3.3) to an HS-like set of 2
in transformations (3.3) to an HS-like set of 2 equations with the even Hamiltonian
equations with the even Hamiltonian  for unknown
for unknown  , we obtain a system of the form (3.2). An extension of the union of the latter HS with Eqs. (3.2) is formally identical to the system (3.2) under the replacement
, we obtain a system of the form (3.2). An extension of the union of the latter HS with Eqs. (3.2) is formally identical to the system (3.2) under the replacement
The iteration sequence related to a reformulation of the antisymplectic gauge transformations of ghost variables  obtained from relations (2.58), leads, for an
obtained from relations (2.58), leads, for an  -stage reducible LSM at the s-th step, with 0 < s < L and
-stage reducible LSM at the s-th step, with 0 < s < L and  , to invariance transformations for
, to invariance transformations for  , modulo the constraints
, modulo the constraints  , namely,
, namely,
The substitution  transforms the antisymplectic gauge transformations (3.4) to rs-1 equations for unknown
transforms the antisymplectic gauge transformations (3.4) to rs-1 equations for unknown  , extended by the superantifields of odd momenta
, extended by the superantifields of odd momenta  (q), into an HS on PT*
(q), into an HS on PT* s-1 =
s-1 = 
Having combined the system (3.5) with an HS in PT* [s-1] =
[s-1] =  of the same form with
of the same form with  and the even BFV-BRST charge (Hamiltonian)
and the even BFV-BRST charge (Hamiltonian)  and having expressed the result for
and having expressed the result for  equations with
equations with  , we obtain, by induction, the following HS:
, we obtain, by induction, the following HS:
The even function  quadratic in the powers of
quadratic in the powers of  with vanishing ghost number provided by the (
with vanishing ghost number provided by the (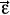 , gh)-spectrum for PT*
, gh)-spectrum for PT* k-coordinates
k-coordinates
is a solution of the classical master equation written in terms of Dirac's antibracket trivially extended in PT* , k = MIN} with accuracy up to
, k = MIN} with accuracy up to  , modulo
, modulo  ,
,
Additionally, the function  is subject to the BFV-like condition of properness in the sense that
is subject to the BFV-like condition of properness in the sense that
where the codimension of the surface  is calculated with respect to PT*
is calculated with respect to PT* CL. The integrability of the HS in (3.8) is guaranteed by a double deformation of
CL. The integrability of the HS in (3.8) is guaranteed by a double deformation of  first in the powers of
first in the powers of  and then in the powers of
and then in the powers of  , in the framework of the existence theorem [3] for the classical master equation in the minimal sector, in the case of a purely topological theory (i.e., one without the potential term S0(A) = S(
, in the framework of the existence theorem [3] for the classical master equation in the minimal sector, in the case of a purely topological theory (i.e., one without the potential term S0(A) = S( (0),0) in Sec. 2.1 presenting the classical action of a standard gauge model for (eP)I = (eP)I =
(0),0) in Sec. 2.1 presenting the classical action of a standard gauge model for (eP)I = (eP)I =  = 0):
= 0):
Theorem 3: There exists a solution of equation (3.9), in PT*
MIN, as a power series in the ghost coordinates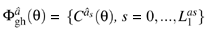 , subject to the boundary conditions
, subject to the boundary conditions
and to the condition of properness (3.8) written for SW;k(q).
A sketch of a proof: the proof of Theorem 3 repeats the Koszul-Tate construction in Hamiltonian formalism [15] for the antisymplectic case.
IV. CONCLUSION
Let us summarize the main results of the present work.
We have examined a q-local description of an arbitrary degenerate reducible superfield theory as a natural extension of a usual gauge theory, defined on a configuration space  of classical fields Ai, to a local superfield model. Namely, we apply Dirac's algorithm to realize an odd Hamiltonization of a Lagrangian degenerate local superfield model (LSM), being an extension of a usual gauge model of classical fields Ai, i = 1,...,n = n++n-, on a configuration space Mcl, to a q-local theory defined on an odd tangent bundle Todd
of classical fields Ai, to a local superfield model. Namely, we apply Dirac's algorithm to realize an odd Hamiltonization of a Lagrangian degenerate local superfield model (LSM), being an extension of a usual gauge model of classical fields Ai, i = 1,...,n = n++n-, on a configuration space Mcl, to a q-local theory defined on an odd tangent bundle Todd
 I,¶qI} , I = 1,...,N = N++N-, (n+,n-) < (N+,N-) with N+,( N-) bosonic (fermionic) superfields. The generalized classical superfields
I,¶qI} , I = 1,...,N = N++N-, (n+,n-) < (N+,N-) with N+,( N-) bosonic (fermionic) superfields. The generalized classical superfields  I(q),
I(q),  I(q) = AI + lIq, parameterize the base
I(q) = AI + lIq, parameterize the base  CL (
CL ( clÌ
clÌ  CL) of the bundle PTCL and transform with respect to a J-superfield representation T of the direct product of supergroups
CL) of the bundle PTCL and transform with respect to a J-superfield representation T of the direct product of supergroups 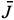 , P: J =
, P: J = 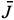 × P, P = exp(iµpq), with
× P, P = exp(iµpq), with 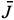 chosen as a spacetime SUSY group, and µ, pq being the respective nilpotent parameter and generator of q-shifts. The non-Lorentz character of superfields
chosen as a spacetime SUSY group, and µ, pq being the respective nilpotent parameter and generator of q-shifts. The non-Lorentz character of superfields  I(q) defined on
I(q) defined on  = {(zM,q)} = {zK} , zM Ì i Ì I, is reflected by a possible inclusion in their spectrum of additional, besides
= {(zM,q)} = {zK} , zM Ì i Ì I, is reflected by a possible inclusion in their spectrum of additional, besides  I(q), superfields corresponding to the ghosts of the minimal sector in the BV quantization scheme. Following the BFV prescription, we construct their q-local counterparts on the basis of a complete system of antisymplectic constraints and a Hamiltonian action
I(q), superfields corresponding to the ghosts of the minimal sector in the BV quantization scheme. Following the BFV prescription, we construct their q-local counterparts on the basis of a complete system of antisymplectic constraints and a Hamiltonian action 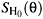 defined on PT*
defined on PT* CL =
CL = 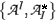 , a bosonic BRST charge SW(q), a unitarizing Hamiltonian action
, a bosonic BRST charge SW(q), a unitarizing Hamiltonian action 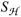 (q), and a gauge fermion FY(q). We specify to the case of a singular LSM a derivation of Lagrangian and Hamiltonian master equations from Noether's first theorem applied to q-shifts, and establish a relation between the complete Hamiltonian action, SH(q) =
(q), and a gauge fermion FY(q). We specify to the case of a singular LSM a derivation of Lagrangian and Hamiltonian master equations from Noether's first theorem applied to q-shifts, and establish a relation between the complete Hamiltonian action, SH(q) = 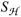 (q)+(SW(q),FY(q))qD, constructed via q-local Dirac's antibracket, and the quantum action of the BV method.
(q)+(SW(q),FY(q))qD, constructed via q-local Dirac's antibracket, and the quantum action of the BV method.
We have constructed an odd-Hamiltonian formulation for an LSM starting from an odd Lagrangian in the case of a degenerate Hessian supermatrix  as the supermatrix of second derivatives of the Lagrangian classical action, SL(q) = SL(
as the supermatrix of second derivatives of the Lagrangian classical action, SL(q) = SL( (q),¶q
(q),¶q (q),q), with respect to odd velocities (¶q
(q),q), with respect to odd velocities (¶q
Acknowledgments D.M.G. thanks the foundations FAPESP and CNPq for permanent support. P.Yu.M. is grateful to CNPq.
[25] An LSM of a general type, unlike an LSM of a special type, contains the operator ¶q º  = d/dq in the structure functions of the gauge algebra.
= d/dq in the structure functions of the gauge algebra.
[26] In the case of a nontrivial relation between the t- and q-components of supertime c by means of the operator D = ¶q + q¶t, [D, D]+ =2¶t, as the generator of the supergroup J, an adequate realization of J, whose quotient is the superspace  , is made possible in terms of (non(super)commutative with each other)
, is made possible in terms of (non(super)commutative with each other) 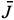 and Pntriv = exp(iµD) by analogy with the construction of a simple SUSY group.
and Pntriv = exp(iµD) by analogy with the construction of a simple SUSY group.
[27] In the infinite-dimensional case, the concept of dimension has to be clarified; for a vector bundle  ®
®  , it is formally understood that dim
, it is formally understood that dim is the dimension of the fiber
is the dimension of the fiber  over an arbitrary p Î
over an arbitrary p Î  .
.
[28] Here, the rank of a supermatrix is calculated with respect to the Grassmann parity
Received on 29 August, 2007
- [1] D.M. Gitman, P.Yu. Moshin, and A.A. Reshetnyak, J. Math. Phys. 46, 072302 (2005); Phys. Lett. B 621, 295 (2005).
- [2] A.A. Reshetnyak, Basic features of general superfield quantization method for gauge theories in Lagrangian formalism, Proceedings of the International Seminar on Supersymmetries and Quantum Symmetries SQS 03, Dubna, Russia, July 24-29, 2003 (Eds. E. Ivanov and A. Pashnev, JINR, Dubna, 2004, 345); hep-th/0312118.
- [3] I.A. Batalin and G.A. Vilkovisky, Phys. Lett. B 102, 27 (1981); Phys. Rev. D 28, 2567 (1983); J. Math. Phys. 26, 172 (1985).
- [4] A.A. Reshetnyak, Russ. Phys. J. 47, 1008 (2004); hep-th/0512327.
- [5] I.A. Batalin and I.V. Tyutin, Int. J. Mod. Phys. A 8, 2333 (1993).
- [6] I.A. Batalin, K. Bering, and P.H. Damgaard, Nucl. Phys. B 739, 389 (2006); hep-th/0512131.
- [7] J. Thierry-Mieg, J. Math. Phys. 21, 2834 (1980); L. Bonora and M. Tonin, Phys. Lett. B 98, 48 (1981); L. Bonora, P. Pasti, and M. Tonin, J. Math. Phys. 23, 839 (1982); L. Baulieu, Phys. Rep. 129, 1 (1985).
- [8] C.M. Hull, B. Spence, and J.L. Vazquez-Bello, Nucl. Phys. B 348, 108 (1991).
- [9] V.N. Shander, Functional analysis and its applications, 14, No. 2 (1980) 91 (in Russian).
- [10] I.A. Batalin, K. Bering, and P.H. Damgaard, Nucl. Phys. B 515, 455 (1998); Phys. Lett. B 446, 175 (1999).
- [11] E.S. Fradkin and G.A. Vilkovisky, Phys. Lett. B 55, 224 (1975); I.A. Batalin and G.A. Vilkovisky, Phys. Lett. B 69, 309 (1977); E.S. Fradkin and T.E. Fradkina, Phys. Lett. B 72, 343 (1978); I.A. Batalin and E.S. Fradkin, Phys. Lett. B 122, 157 (1983); For a review see: M. Henneaux, Phys. Rept. 126, 1 (1985).
- [12] P.M. Lavrov, P.Yu. Moshin, and A.A. Reshetnyak, Mod. Phys. Lett. A 10, 2687 (1995); JETP Lett. 62, 780 (1995); B. Geyer, P.M. Lavrov, and P.Yu. Moshin, Phys. Lett. B 463, 188 (1999);P.M. Lavrov and P.Yu. Moshin, Theor. Math. Phys. 126, 101 (2001).
- [13] M. Alexandrov, M. Kontsevich, A. Schwarz, and O. Zaboronsky, Int. J. Mod. Phys. A 12, 1405 (1997).
- [14] M. Grigoriev and P.H. Damgaard, Phys. Lett. B 474, 323 (2000).
- [15] J.L. Koszul, Bull. Soc. Math. France 78, 5 (1950); A. Borel, Ann. Math. 57, 115 (1953); J. Tate, Illinois J. Math. 1, 14 (1957);J. Stasheff, Deformation theory and the Batalin-Vilkovisky master equation, Proceedings of the Conference on Deformation Theory (Ascona, Switzerland, 1996); q-alg/9702012;J.M.L. Fisch and M. Henneaux, Comm. Math. Phys. 128, 627 (1990).
- [16] M. Henneaux and C. Teitelboim, Quantization of Gauge Systems (Princeton U.P., NJ 1992).
- [17] D.M. Gitman and I.V. Tyutin, Quantization of Fields with Constraints, (Berlin and Heidelberg, Springer-Verlag, 1990).
- [18] I.L. Buchbinder and S.M. Kuzenko, Ideas and Methods of Supersymmetry and Supergravity (Institute of Physics Publishing, Bristol & Philadelphia, 1995).
- [19] E. Noether, Nachr. Ges. Wiss. Goettingen, Math.-Phys. Kl. II (1918) 235; M.A. Tavel, Transport Theory and Stat. Phys. 1, No. 3, 183 (1971).
- [20] B.S. De Witt, Dynamical Theory of Groups and Fields (Gordon & Breach, New York, 1965).
- [21] F.A. Berezin, Introduction to Superanalysis (Eds. A.A. Kirillov and D. Leites, Reidel, Dordrecht, 1987).
- [22] B. De Witt, Supermanifolds (2nd Edition, Cambridge University Press, Cambridge, 1992).
- [23] I.A. Batalin and I.V. Tyutin, Mod. Phys. Lett. A 8, 3673 (1993); Int. J. Mod. Phys. A 9, 1707 (1994).
- [24] A.A. Deriglazov, A.V. Galajinskii, and S.L. Lyachovich, Nucl. Phys. B 177, 282 (1996).
Publication Dates
-
Publication in this collection
28 Jan 2008 -
Date of issue
Dec 2007
History
-
Received
29 Aug 2007








































































