Evolution of chaos in the Matsumoto-Chua circuit: a symbolic dynamics approach

REGULAR ARTICLES

Evolution of chaos in the Matsumoto-Chua circuit: a symbolic dynamics approach

Dariel M. Maranhão; Carmen P. C. Prado

Instituto de Física, Universidade de São Paulo Caixa Postal 66318, 053015-970, São Paulo, SP, Brazil

ABSTRACT

We use symbolic dynamics to follow the evolution of the Matsumoto-Chua circuit in the chaotic regime. We consider the evolution of the whole population of unstable periodic orbits and of the associated trajectories, in four chaotic attractors generated by the circuit. Symbolic planes and first return maps are built for different values of the control parameter. The bifurcation mechanism suggests the possibility of the existence of a homoclinic orbit.

1 Introduction

We use symbolic dynamics to revisit the well-studied Matsumoto-Chua circuit. In this analysis we follow the behavior of the whole population of unstable periodic orbits and of the associated trajectories, in four chaotic attractors generated by Chua's circuit in the chaotic regime. With a convenient embedding, we use a natural partition that seems to elucidate the specific bifurcation mechanism characterizing the evolution of the chaotic regime in the system, for a certain range of the control parameter. We show that there is a pattern in the way new (unstable) periodic orbits are created, which is very similar to the mechanism that leads to a homoclinic orbit in one-dimensional systems. The analysis of the symbolic sequences of the trajectories of the circuit, through its fragmentation patterns [6], reinforces the conjecture that the model may present a homoclinic orbit.

This work is organized as follows. In section 2, we present the Matsumoto-Chua circuit as well as the spiral-like attractors associated with this model for a range of values of the control parameter R. In section 3, we identify and extract the unstable periodic orbits and present the partitions used to codify orbits and trajectories. We discuss the hyperbolic regime and show that the evolution of this circuit is very similar to one-dimensional systems with homoclinic chaos. In section 4, we show how the changes in the dynamics of the circuit affects first return maps, symbolic planes and fragmentation patterns. Finally, in section 5, we summarize our conclusions.

2 The Matsumoto-Chua circuit

The Matsumoto-Chua circuit is a simple electronic circuit made of two capacitors, one linear resistor, one inductor, and one nonlinear diode (see Figs. 1(a) and 1(b)). This circuit is modeled by the equations

where C₁ and C₂ are the capacitors, v₁ and v₂ the tensions across the capacitors C₁ and C₂, R is the linear resistor, L is the inductor, i_L is the current across the inductor L, and h(v₁) is the characteristic curve in the (nonlinear) diode. The function h(v₁) (see Fig.1(b)) is given by

where m₁, m₂, and B_P are constants. We fixed the following values for these parameters: 1/C₁ = 9.0, 1/C₂ = 1.0, 1/L = 7.0, m₁ = -0.5, m₂ = -0.8 and B_P = 1.0; R the control parameter of the model.

As the parameter R changes, the Matsumoto-Chua circuit exhibits a complex and rich behavior. This richness has been explored extensively in previous works (see for example [8]). For R » 1.55, we can identify a symmetric pair of spiral-like attractors that, after a frontier crisis that occurs for R » 1.47, merge into a single attractor called by us ''double-scroll''. In this work we analyze in detail the pair of spiral-like attractors for R = 1.510, R = 1.500, and R = 1.495, which we call A, B, and C, respectively. Because the pair of attractors is symmetric, only one of them needed to be analyzed. The results for attractors A, B, and C, are then compared with results obtained for a forth attractor, D, that appears for a slightly larger value of R = 1.488, right after what may be the the onset of a hyperbolic regime.

All the attractors were obtained from numerical integration of equations 1. As an example, a picture of attractor B can be seen in figure 2(a), together with its first return map (fig. 2(b)). Attractors A, B and C show a similar behavior. Attractor D will be better discussed in section 4.

In order to build the first return maps, we used a Poincaré section defined by

where define one of the fixed points of the attractor. Following [9], and taking advantage of the equivariant symmetry presented by the model, we adopted, for the first return map, a new variable w = |i_L| + |v₂|, where is an empirical factor ( = 1.3 for attractors A, B, C, and 1.2 for attractor D). If the first return map is written in terms of either i_L or v₂, the branches are shown in duplicate, which makes it more difficult to identify the critical points and, consequently, establish the correct partition needed to code the dynamics. In Fig. 2(b) we see that, for attractor B, the first return map has two branches and a single critical point (at w = w_c), as an unimodal map. As usual, we associate the symbol 0 with the left branch (w < w_c) and the symbol 1 with the right branch (w > w_c). We observe essentially the same scenario for attractors A and C. However, that does not happen for attractor D (see Fig. 4(d)). Now the first return map is bimodal, and we will need three symbols to code the dynamics.

3 Unstable periodic orbits and symbolic dynamics

We combined two numerical methods to extract the unstable periodic orbits from attractors A, B, C and D [9]. First, we estimate the positions of the unstable periodic orbits with a method known as close returns [10]. We then refined the estimate employing a Newton-Raphson algorithm, adapted to differential equations [11]. Each periodic orbit can then be identified by a (finite) sequence of points w(i), that are the intersections of the orbit with a Poincaré section (in our case defined by (3)). The sequence of points w(i) is then codified into a symbolic sequence S_i of zeros and ones, following the usual procedure [7,4,5]. The results of applying this procedure to attractors A, B and C are shown in tables I, ^II and ^III, respectively. In the tables, for each orbit, one can see the coordinates i_L and v₂ of the intersections of the orbit with the Poincaré section , its period, and the symbolic sequence that represents it.

The dynamics of the system, in cases where it can be coded by two symbols only (unimodal maps), can be represented by a diagram known as the alternating binary tree (see Fig. 3). The alternating binary tree represents all sequences that form the itinerary; they appear in a specific order, known as ''natural order" [11]. A given orbit is represented by the specific sequence - among all compatibles with its itinerary - that appears most at right in the alternating binary tree. It can be proved that, for unimodal maps [12], if an specific orbit is present in a dynamical system, all the other orbits that precede it according to the natural order will also be present. An inspection of Fig. 3 shows that, periodic orbits of period n, represented by sequences of the form (one followed by (n – 1) zeros) are always at the extreme right of the binary tree. So, the identification of an orbit of the type means that the system has all possible orbits, up to level n.

An orbit predicted by the alternating binary tree, but not found in the dynamical system, is said to have been ''pruned''. Note that, in the case of attractor A, some orbits start to be pruned for n = 5 (see table I). The same behavior can be observed in attractors B and C. But in those cases orbits start to be pruned for n = 7, and n = 8, respectively (see ^{tables II} and ^III). Note that the period 1 orbit represented by the symbolic sequence 0 is not present in any of the attractors.

In one-dimensional maps, as a dynamical system approaches homoclinicity, that is, as the unstable manifold W^u, associated with a saddle cycle or a saddle point approaches and touches a stable manifold W^s, many homoclinic points are created. As a consequence, the dynamics of the system becomes more and more complex, with more and more unstable periodic orbits. After the last tangency between manifolds W^u and W^s, there is an infinite number of homoclinic points. When the homoclinic orbit appears, the dynamics reaches its highest degree of complexity; all possible periodic orbits are present and the alternating binary tree is complete. We then say that the system has reached the hyperbolic regime.

A homoclinic orbit can be represented by the symbolic sequence

_H = 1000... =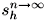 = (100...) [2]. The symbol ''1'' represents the re-injection of the orbit towards the saddle cycle, while the infinite number of symbols ''0'' represent the divergent movement of the orbit around this point. Such an orbit is represented by the last sequence that appears in a complete and infinite alternating binary tree, so the observation of a homoclinic orbit in a dynamical system implies the existence of an infinite number of unstable periodic orbits, of all possible periods. The occurrence of a homoclinic orbit has been identified as the mechanism responsible for the onset of chaos in many dynamical systems. The Rossler attractor [1] and some experimental systems as glow discharge [2] or lasers with a saturable absorber [3] are well-studied examples of more complex systems that have their chaotic behavior associated with the presence of a homoclinic orbit. In such cases the system is said to display homoclinic chaos. The analysis of those dynamical systems has been based on the identification of homoclinic bifurcations [3] - a sequence of saddle-node bifurcations that alternates with period-doubling bifurcations - that leads to the appearance of a homoclinic orbit. The occurrence of such a sequence of bifurcations, before the observation of a homoclinic orbit, has many times been considered sufficient to assume homoclinicity. This sequence induces a ramified structure in first-return maps, builded in a special way so they can capture the number of turns that a trajectory performs around a saddle point (or an unstable hyperbolic saddle cycle [2,3]) before being reinjected in the attractor. Each of the branches of the first-return maps is associated with a specific number of turns that the system gives around the unstable saddle point or cycle.

The extrapolation, for smaller values of the control parameter R, of the sequence of unstable periodic orbits found in attractors A, B and C (and shown, respectively, in tables I, ^II and ^III), allows us to conjecture about the existence of a homoclinic orbit . This is better seen in table IV, which shows, for attractors A, B and C, the last level n for which all sequences predicted by the alternating binary tree have been found. One can observe that the last sequence in the alternating binary tree is, up to some level n, of the form , with increasing values of n for decreasing values of R. The increase in the number of zeros in the orbits of table IV is associated with an increase in the divergent movement around the saddle cycle, in a typical behavior of systems with a homoclinic orbit. This observation gives support to a conjecture that, in the Matsumoto-Chua circuit, as the parameter R decreases, new orbits of period n = (100...0) are created, filling up every level of the binary tree until the hyperbolic regime is attained. The analysis of the symbolic planes and fragmentation patterns gives further support to this conjecture.

4 Symbolic planes

The changes in the dynamics introduced by the development of chaos in the Matsumoto-Chua circuit can be observed both in the first-return maps and in the symbolic planes, for attractors A, B, C, and D.

The symbolic plane gives a way of summarizing the ordering of symbolic sequences in a two-dimensional map. This method has been widely employed to identify topologically similar systems (see examples in references [13], [15] and [14]). Each point (a,b) in a Cartesian plane is associated with a possible sequence in a way described below. If all possible orbits are present, the plane is completely filled. Empty points, represent orbits that have been pruned and are forbidden. From the symbolic plane it is possible to identify the pruning fronts and the kneading sequences.

The coordinates (a, b) of a specific orbit or trajectory is built in a unique way from the symbolic sequence of zeros and ones that represents the orbit, through the following procedure. Let the symbolic sequence

represent a given trajectory. The symbol s₀ (representing the current position of the system) splits the sequence into two parts, a forward sequence given by s₀s₁s₂ ... s_m ... which represents the ''symbolic future'', and a backward sequence ... s_–m ... s_–2s_–1, which represents the ''symbolic past''. The symbolic coordinates (a,b) for the point that will represent this orbit are then given, in binary notation, by

where

where a and b correspond to real numbers, given by

This formalism can be extended to represent a dynamics described by 3 or more symbols (see, for example,[15] and [16]).

In Figs. 4(a), 4(b), 4(c) and 4(d) we can see the first return maps and the symbolic planes for attractors A, B, C and D, respectively. The first return maps of attractors A, B and C show that those attractors have a unimodal behavior, and can essentially be described by a symbolic dynamics made of two symbols. The first-return map for attractor A (R = 1.510) indicates that the system does not have all possible orbits; the symbolic plane shows many forbidden regions (empty regions) together with allowed regions (filled with dots). Comparing with Figs. 4(b) and 4(c) (attractors B and C, for R = 1.500 and R = 1.495, respectively) we notice that the left branch of the first-return map approaches more and more the diagonal, and less orbits are forbidden. Fig.4(c) captures the dynamics in a point with almost no forbidden orbits.

Figure 4(d) (attractor D, with R = 1.488) shows a completely different scenario, with the drastic changes in the behavior of the system that may have been induced by the onset of a homoclinic regime. Now the first-return map is bimodal. The symbolic plane, now built with a dynamics of three symbols, is completely different, with many forbidden regions.

In unimodal maps with a unidimensional structure, the pruning front, in the symbolic plane, is a continuous line, while in two-dimensional maps the pruning front is discontinuous [14]. Fig. 5, an amplification of the symbolic planes presented in Fig. 4, clearly shows that there is a discontinuity in the pruning fronts of attractors A, B and C, indicating that they do have a two-dimensional structure. We see, however, that those pruning fronts get closer and closer to each other as we go from attractor A to C¹. In order to measure how good is the one-dimensional approximation, we can define an index d, equal to the integer part of log₂, where a₁ and a₂ define the smaller and larger pruning fronts, respectively. The index d gives the level, in the binary tree, up to which the behavior of the system can be considered one-dimensional. For instance, for attractor A, a₁ = 0.9472 and a₂ = 0.9605, so d_A = 4. Analogously, d_B = 7 and d_C = 11. Those results show that the one-dimensional approximation becomes better and better as the chaotic regime evolves.

We are aware that, if we have a 2D map, the existence of a 10ⁿ orbit does not force the existence of all previous orbits of the natural sequence, as it happens in 1D maps. However, we think that we have strong indications that, at least in these case, as the chaotic regime evolves and the dynamics of the system becomes more and more one-dimensional, it approaches the dynamical behavior of a typical unimodal map, and our observations may in fact indicate the existence of homoclinic chaos. It would be interesting to observe if, in other systems, for which it is well established that the hyperbolic regime is reached, the same scenario is found.

The fragmentation patterns (see Fig. 6) give another way of showing that Chua's circuit may be approaching a homoclinic regime. Through those patterns one can build a pictorial representations of the symbolic sequences that represent the trajectories. We associate a black block with symbol 1 and a white block with symbol 0. For instance, the sequence 100 would be represented by the sequence of blocks ''black-white-white''. The blocks are placed in sequence, side by side, from left to right, up to 50 blocks; after that, a new row of symbols is added on top of the previous one. The process continues until a grid of 50 × 50 blocks is built. As the chaotic regime evolves, the allowed trajectories will present an increasing number of symbols 0, associated with the divergent movement around the saddle cycle, as compared to the number of symbols ''1'', associated with the reinjection movement.

By visual inspection, it is possible to see that the orbits of attractor A (Fig. 6a) have a predominance of symbols 1 (black blocks), while in attractor C (Fig. 6c) there is a predominance of symbols 0, reflecting the fact that, as the parameter R decreases, the trajectories stay longer and longer in a divergent movement around the saddle cycle.

5 Conclusions

In conclusion, we have extracted the unstable periodic orbits from attractors A, B, C and D of the Matsumoto-Chua circuit. We have used symbolic dynamics in order to show that as the chaotic regime evolves the Matsumoto-Chua circuit has a dynamics that is increasing one-dimensional. We have presented numerical evidence that a homoclinic orbit may be present in the Matsumoto-Chua circuit. The attractors of the dynamics of the circuit were analyzed for four different values of the control parameter R, R Î [1.510, 1.4888]. We found that there is a pattern in the way new unstable periodic orbits are created as the control parameter R is continuously decreased. From this pattern, if the system had a truly 1D dynamics, it would be possible to infer the existence of a homoclinic orbit. If this behavior comes to be checked in similar systems, it will be a new approach to the problem of identifying the onset of homoclinicity that could be used in many other problems, either in experimental situations or numerical simulations.

For each of the studied attractors (attractors A, B and C), we have extracted the unstable periodic orbits, built first-return maps, codified the dynamics and ordered the orbits according to the natural order in an alternating binary tree. It has been possible to see that the last orbit in the diagram, before orbits start to be pruned, was always of the form , with n ® ¥ as the parameter R decreases. Every level of the binary tree is then filled up as in a one-dimensional map, until the hyperbolic regime is attained. We conjecture that, because the behavior of the system becomes close to a one-dimensional map, maybe a homoclinic orbit exists in this circuit.

We also built symbolic planes and fragmentation patterns for all the studied sequences and trajectories, which gives further support to our conjecture.

6 Acknowledgements

We acknowledge the financial support of the Brazilian agency CNPq.

References

[1] P. Gaspard, R. Kapral, G. Nicolis, J. Stat. Phys. 35, 697 (1984).

[2] T. Braun, J. A. Lisboa, Int. J. Bifurc. Chaos, 4, 1483 (1994).

[3] F. Papoff, A. Fioretti, E. Arimondo, Phys. Rev. A 44, 4639 (1991).

[4] J. Plumecoq, M. Lefranc, Physica D 144, 231 (2000).

[5] N. B. Tufillaro, T. Abbott, J. Reilly, An experimental approach to nonlinear dyanamics and chaos (Addison-Wesley, California, 1992).

[6] W. M. Gonçalves, R. D. Pinto, J. C. Sartorelli, Physica D 134, 267 (1999).

[7] J. Milnor and W. Thurston, in Dynamical Systems, ed. J. Alexander, Lecture Notes in Math. 1342, spring-Verlag, Berlin, (1988).

[8] R. N. Madan, Chua's circuit: a paradigm for chaos, (World Scientific, Singapore, 1993).

[9] C. Letellier, P. Dutertre, G. Gouesbet, Phys. Rev. E 49, 3492 (1994).

[10] D. P. Lathrop, E. J. Kostelich, Phys. Rev. A 40, 4028 (1989); G. B. Mindlin, Gilmore, Physica D 58, 229 (1992).

[11] B. -L. Hao, Elementary Symbolic Dynamics and Chaos in Dissipative Systems, (World Scientific, Singapore, 1984).

[12] P. Glendinning, C. Laing, Phys. Letters A 211, 155 (1996); S. V. Gonchenko, L. P. Shilnikov and D. V. Turaev, Chaos 6, 15 (1996); R. L. Devaney, An introduction to chaotic dynamical systems, (Addison-Wesley, second ed., Boston 1988).

[13] A. Tufaile, J. C. Sartorelli, Phys. Lett. A 275, 211 (2000).

[14] P. Civitanovic, G. H. Gunaratne and I. Procaccia, Phys. Rev. A 38, 1503 (1988).

[15] C. Letellier, G. Gouesbet and N. F. Rulkov, Int. J. Bifurc. Chaos 6, 2531 (1996).

[16] J.-X. Liu, W. -M. Zheng and B. -L. Hao, Chaos, Solitons and Fractals 7, 1427 (1996).

Received on 21 July, 2004

1

notice that, in order to show the existence of a discontinuity, the scales of each symbolic plane of

Fig. 5 are not the same.

Publication Dates

• Publication in this collection
  03 May 2005
• Date of issue
  Mar 2005

History

• Accepted
  21 July 2004
• Received
  21 July 2004