High overtones of dirac perturbations of a Schwarzschild black hole and the area spectrum of quantum black holes

Abstract

We find high overtones of the Dirac quasi-normal (QN) spectrum of a Schwarzschild black hole (Sbh), by Leaver's method. At high overtones, the spacing of the imaginary part of the QN spectrum is equidistant (Im omegan+1- Im omegan = i/8M , where M is the black hole mass). This can also be analytically obtained by means of a Born approximation. At high overtones, the real part of omegan goes to zero. Finally, we comment this result in the context of Hod's conjecture on highly damped QNMs and the area spectrum of (quantum) black holes.

High overtones of dirac perturbations of a Schwarzschild black hole and the area spectrum of quantum black holes

Karlúcio H. C. Castello-Branco^{I, II}; Roman A. Konoplya^I; Alexander Zhidenko^III

^IInstituto de Física, Universidade de São Paulo (Brazil)

^IIDepartamento de Física, Universidade Federal de Ouro Preto (Brazil),

^IIIDepartment of Physics, Dniepropetrovsk National University (Ukraine)

ABSTRACT

We find high overtones of the Dirac quasi-normal (QN) spectrum of a Schwarzschild black hole (Sbh), by Leaver's method. At high overtones, the spacing of the imaginary part of the QN spectrum is equidistant (Im w_n+1- Im w_n = i/8M , where M is the black hole mass). This can also be analytically obtained by means of a Born approximation. At high overtones, the real part of w_n goes to zero. Finally, we comment this result in the context of Hod's conjecture on highly damped QNMs and the area spectrum of (quantum) black holes.

Introduction.

Quasinormal Modes (QNMs) are an important characteristic of a black hole. They dominate the late-time response of a black hole to external perturbations, being independent on the way of its excitation. They provide the "fingerprints" of a black hole, feasible to be seen in the detection of gravitational waves (for a review, see [1]). Furthermore, the importance of black holes QN spectra is not limited by the observational aspects of gravitational waves. In fact, QNMs of black holes in Anti-de-Sitter (AdS) spaces have an interpretation in the dual Conformal Field Theory (CFT) which "lives" on the (conformal) boundary of the space [2]. So, QNMs of black holes in AdS spaces provide a test of the AdS/CFT correspondence [3]. For de-Sitter (dS) space-times, there is also a similar result, since QNMs due to scalar perturbations in the bulk of an empty dS space correspond to decaiyng modes in a dual CFT on the boundary [4], what gives support in favor of the existence of a dS/CFT correspondence. Since (A)dS/CFT correspondences are considered as realizations of the Holographic Principle [5], QNMs play some hole in the description of quantum aspects of gravity. Furthermore, there was also a suggestion that the asymptotic, highly damped QNMs of black holes are connected with a free-parameter that appears in the ensuing area spectrum of Loop Quantum Gravity (LQG). This parameter must be fixed in order that LQG can reproduce the Bekenstein-Hawking entropy [6]. This stimulated considerable interest in the study of QNMs of black holes in flat, dS and AdS backgrounds (for reviews, see [7]). The idea that the QNMs of a black hole might fix the spacing of its quantum area spectrum was suggested by Hod [8], who, based on Bohr's correspondence principle, proposed that the real part of the highly damped QNMs of a Sbh could fix the spacing of its area spectrum. Hod's work relies on Bekenstein's heuristic result that the area spectrum of a stationary quantum black hole would be given by A_n = g · n, with n = 1,2,... , where = (in units G = c = 1) and g , a dimensioless constant, is the spacing of the spectrum (for a review, see [9]). Hod then proposed that if we consider that the mass (energy) of a (quantum) Sbh undergoes a variation dM = Re w , where Re w is the real part of the asymptotic, highly damped QNMs, the area spacing can be fixed as g = 4 ln 3 . At the time of Hod's work, only an expression obtained numerically for the (gravitational) asymptotic, highly damped modes was known [10], namely, Re w = 0.0437123 M^-1 . Hod expressed this as Re w = (ln3)/8pM (in units G = c = 1). Such a result was later analytically obtained by Motl and Neitzke, who showed that it is valid also for asymptotic QNMs due to a scalar perturbation [11]. After the works of Dreyer [6] and, specially, that of Motl and Neitzke [11], Hod's proposal atracted attention and a plenthora of works appeared in the literature, addressing the issue of the area spectrum of quantum black holes and QNMs (for reviews, see [7]). Nevertheless, most works have been mainly concerned on QNMs due to perturbations of integer-spin fields only (gravitational, electromagnetic, and scalar). Although perturbations of half-spin fields were considered by some authors, they were limited to low overtones, by the time we published our results in [12] (see references therein). Motivated by this, we investigated the high overtone behavior of the QN spectrum of the Dirac perturbations of a Sbh [12].

Dirac perturbations of a Schwarzschild black hole.

The Dirac equation in a curved space is given by [13] (g^a e (¶_m+ G_m)+ Y = 0 , where m is the mass of the Dirac field, are tetrads, defined through the metric, g_mn , by g_mn = h_ab

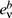, where h_ab = diag(-1,1,1,1) is the Minkowski metric; G_m is the spin conection, given by G_m= 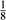[g^a, g^b] 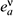e_bn;µ , where g^a are the Dirac matrices and e_bn;µ denotes the covariant derivative of e_bn [13]. In the background of a Sbh, whose metric in spherical-like coordinates is ds² = -f(r)dt² + 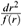+ r² (dq² + sin² qdf²) , where f(r) = 1-(2M/r) and M is the black hole mass, the equation for the time-independent perturbation of a massless Dirac field can be reduced to the wave-like equation [13] ( 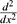+ w² -V(x))y (x) = 0 , where x is defined by dx = dr/f(r) and V(x) is [14]

where µ = ± (j+ ) , with j = ± , being the multipole index. Since V± are supersymetric potentials, they have the same associated spectrum of QNMs [14]. So we can choose, for instance, V+ to make our analysis. In terms of x , V(x) º V(r(x)) goes to zero at both boundaries, i.e., V(x ® ¥)® 0 . Choosing the phase e^-iwt , the QNMs satisfy the boundary conditions y(x) ~ e^±iwx , for x® ¥ , corresponding to purely in-going waves at the black hole event horizon and purely out-going waves at infinity.

Determination of the QNMs.

In [12] we have determined the QNMs by means of Leaver's method [15], which resorts to the Fröbenius method to express the solution of the perturbation equation in terms of the radial variable r . Leaver's method consists in expressing the solutions of the perturbation equation, in terms of r , by a power series, with the boundary conditions for QNMs translated into a convergence condition to the series, which can be expressed as an equation involving infinite continued fractions. The coefficients of the expansion are determined via a recurrence relation whose coefficients will be functions of w . Then the QN frequencies will correspond to those values of w such that the power series converges at r = ¥ [15]. Then, following [15], we can choose y(x) = e^±iwxu(x) , where u(r) has a regular singularity at the event horizon and is finite at x®¥ , such that the series u(r) = f(r)^2s _{= 0} a_nf(r)^n/2 converges at r = ¥ . From these and the wave-like equation, a three-term recurrence relation can be obtained and when w is a QN frequency, the ratio of the coefficients of the series is finite and can be found through continued fractions [15], such that we are left with an implicit equation for w , in terms of inverted continued fractions. The QNMs are the roots of an inverted continued fraction (for details, see [12]). High overtones. The main difference from what we know on the high damping regime for perturbations of fields of integer spin (scalar, gravitational, and electromagnetic) is that now the spacing in imaginary part is not i/4M , as it takes place for integer-spin perturbations, but i/8M . It can be seen numerically that highly damped QNMs display the following asymptotic behaviour: Re w_n» 0 ; Im w_n+1 - Im w_n» - i/8M , as n®¥ . This formula for the spacing of the imaginary part can be reproduced following Ref.[16], where the spacing was derived by determining the poles of the scattering amplitude in the fist Born approximation, in the case of integer-spin perturbations of a Sbh. For highly damped modes we can use the Born approximation, where the scattering amplitude is given by the formula [16] S(k) = V(x) e^{2 i k x}dx . Using Eq.(1) for V(x), we found S(k) ~ combinations of G(4ikM) and G((1/2) + 4ikM) . The poles of the amplitude occur when (1/2) + 4 i M k = - n , or 4iMk = - n (n > 0 and is integer), i.e., k_n = in/8M is the spacing for the imaginary part of the highly damped QNMs.

Concluding Remarks.

In [12], we have studied the highly damped regime of the Dirac QN spectrum of a Sbh. The spacing of the imaginary part were found to be twice less than that for integer-spin fields. As was shown both numerically and analytically in [17], the real part of the highly damped QNMs for scalar and gravitational perturbations of a Sbh asymptotically approaches a constant, equal to (ln3)/8pM (G = c = 1), whereas for electromagnetic perturbations, it goes to zero [18]. For the highly damped QNMs of Dirac perturbations, we have found that Re w also goes to zero. According to Hod's conjecture [8], this would simply imply a null value for the spacing of the area spectrum of a Sbh. Thus the black hole would have a continuous area spectrum. Since the real part of the highly damped QNMs does not have a universal value for all kinds of perturbing fields in the case of a Sbh, the simplest spherical four-dimensional black hole solution, it seems the role of QNMs on the area quantization of black holes is puzzling.

Acknowledgements.

K. H. C.-B. and R. K. are grateful to FAPESP (Brazil).

References

[1] K. Kokkotas and B. Schmidt, gr-qc/9909058.

[2] D. Birmingham, I. Sachs, and S. N. Solodukhin, Phys. Rev. Lett. 88, 151301 (2002).

[3] O. Aharony, S. S. Gubser, J. Maldacena, H. Ooguri, and Y. Oz, Phys. Rept. 323, 183-386 (2000).

[4] E. Abdalla, K. H. C. Castello-Branco, and A. Lima-Santos, Phys. Rev. D66 104018 (2002);

[5] R. Bousso, Rev. Mod. Phys. 74, 825-874 (2002).

[6] O. Dreyer, Phys. Rev. Lett. 90, 081301 (2003).

[7] E. Berti, gr-qc/0411025; J. P. S. Lemos, gr-qc/0507101.

[8] S. Hod, Phys. Rev. Lett. 81, 4293 (1998).

[9] J. D. Bekenstein, gr-qc/9808028.

[10] H.-P. Nollert, Phys. Rev. D47, 5253 (1993).

[11] L. Motl and A. Neitzke, Adv. Theor. Math. Phys. 7, 307 (2003).

[12] K. H. C. Castello-Branco, R. Konoplya, and A. Zhidenko, Phys. Rev. D71, 047502 (2005).

[13] D. R. Brill and J. A. Wheeler, Rev. Mod. Phys. 29, 465 (1957).

[14] S. Chandrasekhar, The Mathematical Theory of Black Holes (Clarendon, Oxford, 1983).

[15] E. M. Leaver, Proc. Roy. Soc. Lond. 402, 285 (1985)

[16] A. Medved, D. Martin, and Visser, gr-qc/0310009; T. Padmanabhan, Class. Quant. Grav 21, L1 (2003).

[17] L. Motl, Adv. Theor. Math. Phys. 6, 1135 (2003); E. Berti and K. Kokkotas, Phys. Rev. D68, 044027 (2003).

[18] V. Cardoso, J. Lemos, and S. Yoshida, Phys. Rev. D69, 044004 (2004).

Received on 15 October, 2005

Publication Dates

• Publication in this collection
  16 Jan 2006
• Date of issue
  Dec 2005

History

• Received
  15 Oct 2005