Resumos
O regime eólico de uma região pode ser descrito por distribuição de frequências que fornecem informações e características extremamente necessárias para uma possível implantação de sistemas eólicos de captação de energia na região e consequentes aplicações no meio rural em regiões afastadas. Estas características, tais como a velocidade média anual, a variância das velocidades registradas e a densidade da potência eólica média horária, podem ser obtidas pela frequência de ocorrências de determinada velocidade, que por sua vez deve ser estudada através de expressões analíticas. A função analítica mais adequada para distribuições eólicas é a função de densidade de Weibull, que pode ser determinada por métodos numéricos e regressões lineares. O objetivo deste trabalho é caracterizar analítica e geometricamente todos os procedimentos metodológicos necessários para a realização de uma caracterização completa do regime eólico de uma região e suas aplicações na região de Botucatu - SP, visando a determinar o potencial energético para implementação de turbinas eólicas. Assim, foi possível estabelecer teoremas relacionados com a forma de caracterização do regime eólico, estabelecendo a metodologia concisa analiticamente para a definição dos parâmetros eólicos de qualquer região a ser estudada. Para o desenvolvimento desta pesquisa, utilizou-se um anemômetro da CAMPBELL.
função de densidade; velocidade eólica; potência eólica
The wind regime of a region can be described by frequency distributions that provide information and features extremely necessary for a possible deployment of wind systems of energy capturing in the region and the resulting applications in rural areas in remote regions. These features, such as the annual average speed, variance of speed and hourly average of wind power density, can be obtained by the frequency of occurrences of certain speed, which in turn should be studied through analytical expressions. The analytic function more suitable for wind distribution is the density function of Weibull, which can be determined by numerical methods and linear regression. The objective of this study is to characterize analytically and geometrically all methodological procedures necessary to carry out a full characterization of the wind regime of a region and its applications in Botucatu-SP to determine the energy potential for implementation of wind turbines. Thus it was possible to make statements of theorems related to how to characterize the wind regime, establishing a concise analytical methodology for defining the wind parameters of any region to be studied. For the development of this research, it was used a CAMPBELL anemometer.
density function; wind speed; wind power
ARTIGOS CIENTÍFICOS
ENERGIA NA AGRICULTURA
Caracterização analítica e geométrica da metodologia geral de determinação de distribuições de Weibull para o regime eólico e suas aplicações
Analytical and geometric characterization of general methodology of determination of Weibull distribution for wind regime and its applications
Luís R. A. Gabriel FilhoI; Camila P. CremascoII; Odivaldo J. SeraphimIII; Fernando de L. CaneppeleIV
ILicenciado em Matemática, Professor Doutor, Universidade Estadual Paulista, Câmpus de Tupã - SP, Fone: (0XX14) 3404-4200, gabrielfilho@tupa.unesp.br
IILicenciada em Matemática, Professora Doutora, Faculdade de Tecnologia de Presidente Prudente - SP, Fone: (0XX18) 3916-7887, camila@fatecpp.edu.br
IIIEngº Eletricista, Professor Livre Docente, Universidade Estadual Paulista, Câmpus de Botucatu, Botucatu - SP, Fone: (0XX14) 3811-7165, seraphim@fca.unesp.br
IVEngº Eletricista, Professor Mestre, Universidade Estadual Paulista, Câmpus de Itapeva - SP, Fone: (0XX15) 3524-9100, fernando@itapeva.unesp.br
RESUMO
O regime eólico de uma região pode ser descrito por distribuição de frequências que fornecem informações e características extremamente necessárias para uma possível implantação de sistemas eólicos de captação de energia na região e consequentes aplicações no meio rural em regiões afastadas. Estas características, tais como a velocidade média anual, a variância das velocidades registradas e a densidade da potência eólica média horária, podem ser obtidas pela frequência de ocorrências de determinada velocidade, que por sua vez deve ser estudada através de expressões analíticas. A função analítica mais adequada para distribuições eólicas é a função de densidade de Weibull, que pode ser determinada por métodos numéricos e regressões lineares. O objetivo deste trabalho é caracterizar analítica e geometricamente todos os procedimentos metodológicos necessários para a realização de uma caracterização completa do regime eólico de uma região e suas aplicações na região de Botucatu - SP, visando a determinar o potencial energético para implementação de turbinas eólicas. Assim, foi possível estabelecer teoremas relacionados com a forma de caracterização do regime eólico, estabelecendo a metodologia concisa analiticamente para a definição dos parâmetros eólicos de qualquer região a ser estudada. Para o desenvolvimento desta pesquisa, utilizou-se um anemômetro da CAMPBELL.
Palavras-chave: função de densidade, velocidade eólica, potência eólica.
ABSTRACT
The wind regime of a region can be described by frequency distributions that provide information and features extremely necessary for a possible deployment of wind systems of energy capturing in the region and the resulting applications in rural areas in remote regions. These features, such as the annual average speed, variance of speed and hourly average of wind power density, can be obtained by the frequency of occurrences of certain speed, which in turn should be studied through analytical expressions. The analytic function more suitable for wind distribution is the density function of Weibull, which can be determined by numerical methods and linear regression. The objective of this study is to characterize analytically and geometrically all methodological procedures necessary to carry out a full characterization of the wind regime of a region and its applications in Botucatu-SP to determine the energy potential for implementation of wind turbines. Thus it was possible to make statements of theorems related to how to characterize the wind regime, establishing a concise analytical methodology for defining the wind parameters of any region to be studied. For the development of this research, it was used a CAMPBELL anemometer.
Keywords: density function, wind speed, wind power.
INTRODUÇÃO
Muitas propriedades e comunidades rurais no Brasil, principalmente nas regiões Norte e Nordeste, não são atendidas com energia elétrica, pois estão distantes das centrais de geração de eletricidade. Uma das formas de garantir o suprimento de energia elétrica nessas propriedades ou comunidades rurais isoladas seria a implantação de sistemas energéticos baseados em fontes alternativas de energia (KOLLING et al., 2004).
Segundo MARINI & ROSSI (2005), o suprimento energético a comunidades rurais isoladas e a áreas remotas tem sido um constante desafio, principalmente nos países subdesenvolvidos ou em desenvolvimento, devido às enormes disparidades econômicas e sociais e, muitas vezes, às dimensões geográficas desses países.
Em virtude desta necessidade energética, faz-se necessário o estudo de fontes alternativas de energia que independam de redes de distribuição, tal como a energia eólica (GABRIEL FILHO, 2007). Porém, a viabilidade de instalação de turbinas eólicas requer estudos prévios para o conhecimento da variação e do regime anual das correntes eólicas e suas magnitudes, sendo assim necessária a realização de estimativas do aproveitamento da energia eólica por distribuições de probabilidade.
Os registros da densidade de probabilidade ganham importância se puderem ser descritos por expressões analíticas. Têm sido sugeridas várias distribuições probabilísticas para descrever o regime de ventos, mas, segundo SILVA et al. (2002), a distribuição de Weibull (WEIBULL, 1951) é normalmente considerada como a mais adequada. A expressão matemática da função densidade de probabilidade de Weibull é dada por:
quando u > 0, e , f (u) = 0 quando u < 0 , em que,
u - velocidade média do vento;
c - parâmetro de escala, com as dimensões de velocidade, e
k - parâmetro de forma, sem dimensões.
Tais parâmetros c e k são fundamentais para o estudo da maioria das distribuições existentes e, uma vez obtidos, é possível caracterizar analiticamente as frequências de distribuição do vento através da função densidade de probabilidade de Weibull.
Outras importantes características eólicas são a velocidade média anual do vento uma e a variância σ 2 que, segundo CASTRO (2004), são calculadas por meio das relações:
Outra característica fundamental a ser observada em distribuições eólicas é a densidade de potência média. Esta densidade é determinada instantaneamente em um fluxo de ar através de uma unidade de área normal ao fluxo pela relação:
em que,
u - velocidade instantânea, e
ρ - densidade do ar.
Para o cálculo desta potência média anual, encontra-se a "velocidade cúbica média anual do vento", pela relação  u3f(u) du e, desta forma, a densidade de potência média é dada por:
u3f(u) du e, desta forma, a densidade de potência média é dada por:
O objetivo deste trabalho é estudar analítica e geometricamente todos os procedimentos metodológicos necessários para a realização de uma caracterização completa do regime eólico de uma região. Desta forma, tais estudos analíticos permitem a determinação do potencial energético para implementação de turbinas eólicas. Além disto, foram realizadas aplicações da teoria desenvolvida neste trabalho, na região de Botucatu-SP.
MATERIAL E MÉTODOS
A parte experimental desta pesquisa foi desenvolvida no Núcleo de Energias Alternativas e Renováveis - NEAR, do Laboratório de Energização Rural do Departamento de Engenharia Rural da UNESP, Faculdade Ciências Agronômicas, Fazenda Experimental Lageado, localizado no município de Botucatu - SP.
A velocidade do vento instantânea foi medida com o anemômetro RM-YOUNG WIND MONITOR da CAMPBELL (Figura 1). O anemômetro foi instalado em uma torre a dez metros de altura do solo e possui sensibilidade mínima de 1,0 m s-1 .
A análise foi realizada utilizando-se de registros de velocidade do vento, durante o período de setembro de 2004 a setembro de 2005. Para esta descrição estatística do regime de ventos, determinou-se o número de ocorrências de cada velocidade média horária. Assim, constitui-se uma distribuição discreta da velocidade média do vento em classes de 1 m s-1 .
Um sistema de aquisição de dados meteorológicos foi programado para efetuar leituras a cada 10 segundos e fazer médias e totalizações dos valores lidos a cada 5 minutos. Os dados tabelados foram organizados em médias horárias de velocidade. Os dados coletados foram utilizados nas simulações com relações desenvolvidas neste trabalho.
Além disto, no local em estudo, tais dados observados pelo anemômetro à altura de 10 metros foram corrigidos para valores equivalentes a 14 m, devido ao fato da necessidade da instalação de novos aerogeradores nesta altura.
Esta correção pode ser realizada, segundo CASTRO (2004), utilizando a Lei de Prandtl, em que, onda na prática, é aplicada com a relação:
em que,
u1 - velocidade do vento para a altura h1 = 10 m;
u2 - velocidade do vento para a altura h2 = 14 m; e
h0 - comprimento característico da rugosidade do solo, com seus valores típicos apresentados na Tabela 1.
Devido à existência de algumas árvores próximas à região de medição, adotou-se o valor médio dos limites estabelecidos na Tabela 1 para a classificação "Terreno com árvores", ou seja, h0 = 0,2 . Assim, pela eq.(6), tem-se que:
o que acarretou a necessidade da multiplicação dos dados observados de velocidade do vento pela constante 1,086.
Para o cálculo dos parâmetros de escala e de forma, utilizou-se um método bastante difundido, envolvendo regressão linear, que utiliza a função probabilidade acumulada F(u), representando a probabilidade de uma variável aleatória t exceder o valor u , e é dada por:
em que, f (t) representa uma distribuição qualquer.
A determinação da função probabilidade acumulada de Weibull foi realizada utilizando métodos numéricos aplicados na distribuição discreta de frequências da velocidade, em que quando u0 fosse a velocidade máxima nesta distribuição, calculou-se F(u) = f(t)dt pelo método de integração trapezoidal, fazendo:
f(t)dt pelo método de integração trapezoidal, fazendo:
em que se considerou a partição {0,u0,...,un } com pontos consecutivos distantes entre si do valor Δu .
A determinação do grau de ajuste das séries observadas no modelo de Weibull foi verificada pelo erro residual calculado por:
em que,
Fobs - probabilidade acumulada observada, e
F(calc) - probabilidade acumulada calculada através do modelo de Weibull.
O valor de Fobs foi obtido pelo método de integração trapezoidal representada pela eq.(9), enquanto o de F(calc) foi obtido pela função probabilidade acumulada F .
Em virtude de os parâmetros de escala (c) e de forma (k) serem fundamentais para o estudo da maioria das distribuições existentes, avaliaram-se suas influências nas distribuições. Para isto, foi preciso relacionar a velocidade média anual do vento, a variância e a densidade de potência média com a função Gama, muito conhecida no meio acadêmico e amplamente encontrada em vários softwares como Mathematica, Matlab e Microsoft Excel, e definida da forma:
Por fim, para o cálculo da densidade de potência média Pmed, utilizou-se a densidade do ar ρ= 1,24 no período em estudo, segundo GABRIEL FILHO (2008).
RESULTADOS E DISCUSSÃO
Dados registrados pelo anemômetro
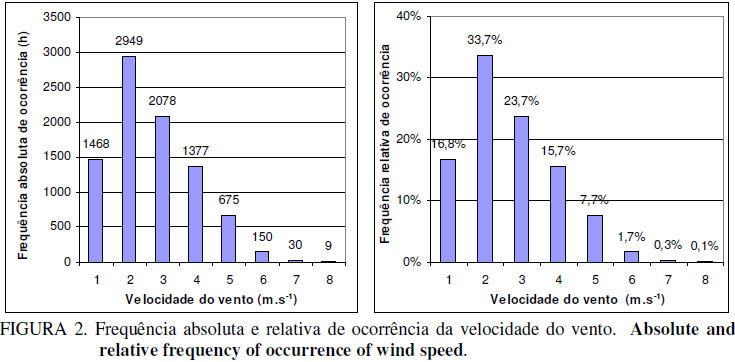
Os dados totalizaram 8.736 horas de registros coletados e sua classificação, com dados já corrigidos para a altura de 14 m, segundo a Lei de Prandtl, sendo estabelecida em classes de frequência de 1 m s-1. Assim, foi possível determinar as frequências absoluta e relativa para cada classe de velocidade, conforme ilustra a Figura 2.
Distribuição de Weibull
A necessidade da determinação da função densidade de probabilidade de Weibull é devida à possibilidade de caracterizar analiticamente as freqüências ilustradas na Figura 2. Para isto, deve-se obter a função probabilidade acumulada de acordo com a eq.(7), que é determinada pelo teorema a seguir.
Teorema 1: A função probabilidade acumulada para a distribuição de Weibull é dada por:
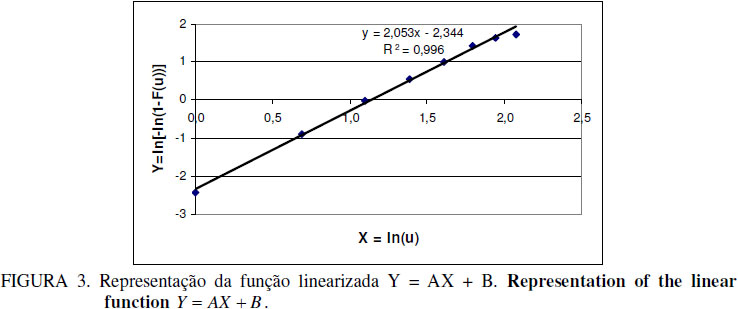
A eq.(12) pode ser expressa como uma função linear do tipo Y = AX + B , com Y = ln {- ln [1 - F(u)]}, X = ln u , A = k e B =-k ln c , pois:
Desta forma, após determinadas as constantes A e B, obtemos os parâmetros desejados, fazendo k = A e c = exp  pois:
pois:
Frente ao exposto, determinada a função probabilidade acumulada de Weibull, é possível calcular os parâmetros de escala e de forma. Assim, inicialmente, utilizando o método apresentado na eq.(9) para a distribuição da região de Botucatu, e fazendo Δu = 1, ui = i +1e n = 7 , obtém-se:
Calculando os valores da função linear Y = AX + B com os dados da Figura 2, é possível construir a Tabela 2.
Os pontos obtidos da função linearizada permitiram ajustar uma função dada por: Y = 2,053 X - 2,344 com R2 = 0,996, caracterizando uma excelente modelagem geométrica (Figura 3).
Logo, tem-se que A = 2,053 e B = -2,344 e, portanto, como k = A e c = exp , pode-se concluir que os parâmetros procurados são k = 2,053 e c = 3,132. Substituindo tais parâmetros na função densidade de probabilidade de Weibull, é possível encontrar a função seguinte e seu gráfico é representado na Figura 4:
, pode-se concluir que os parâmetros procurados são k = 2,053 e c = 3,132. Substituindo tais parâmetros na função densidade de probabilidade de Weibull, é possível encontrar a função seguinte e seu gráfico é representado na Figura 4:
Assim, a Figura 4 representa analiticamente a distribuição ilustrada na Figura 2, apresentando um erro residual de E = 3,2%, enquanto a função probabilidade acumulada é dada por:
Os valores característicos relacionados à distribuição de Weibull indicam que os parâmetros de forma (k) e escala (c) são dados, respectivamente, por 2,053 e 3,132, com um erro residual (E) de 3,20%.
Características eólicas
Os resultados a seguir caracterizam a função gama e suas relações com a velocidade média anual do vento, a variância e a densidade de potência média.
Lema 1: Para qualquer número natural m , tem-se que:
Teorema 2: A velocidade média anual do vento é dada por:
Teorema 3: A variância da frequência da velocidade do vento é dada por:
Teorema 4: A densidade de potência média do vento é dada por:
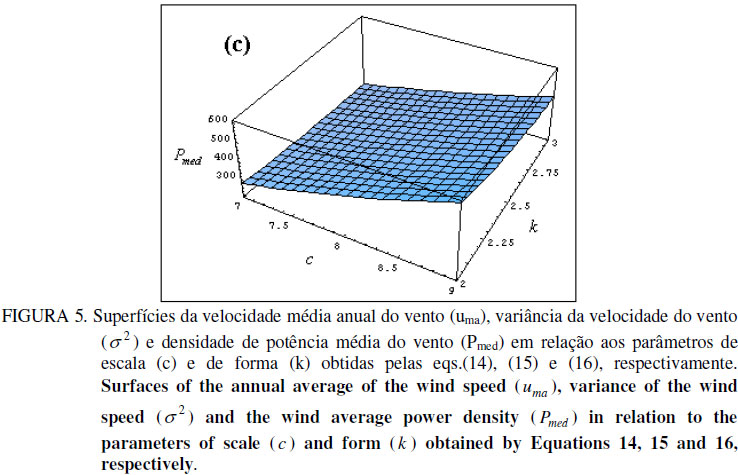
Segundo CASTRO (2004), k é tomado habitualmente como uma medida da dispersão da velocidade do vento e c como uma medida do "vento" disponível. Isto pode ser verificado na Figura 5(b), na qual um aumento no valor de k representa diminuições acentuadas no desvio-padrão; e na Figura 5(a), na qual se observa uma relação diretamente proporcional entre c ea uma. A densidade de potência média do vento, devido ao parâmetro cúbico na eq.(18), é fortemente dependente de c , como é possível observar na Figura 5(c). Como a influência de c é associada à medida de vento disponível, esta dependência era esperada.
Utilizando as eqs.(16), (17) e (18), é possível calcular a velocidade média anual uma, a variância das observações de velocidade do vento σ 2 e a densidade de potência média Pmed dadas, respectivamente, por: uma = 2,77 m s-1 , σ 2 = 0,31 , Pmed = 24,58 W m-2 .
Assim, obtém-se o desvio-padrão σ = 0,55 e o coeficiente de variação C.V. =  = 20% , que, juntamente com a velocidade média anual 2,77 m s-1 e a densidade de potência média 24,58 W m-2, constituem as características eólicas da Fazenda Lageado de Botucatu - SP.
= 20% , que, juntamente com a velocidade média anual 2,77 m s-1 e a densidade de potência média 24,58 W m-2, constituem as características eólicas da Fazenda Lageado de Botucatu - SP.
CONCLUSÕES
Em virtude da caracterização da distribuição de frequências do vento obtida nas medições realizadas pelo anemômetro na Fazenda Lageado, em Botucatu, pela função de densidade de Weibull, será possível realizar futuras comparações desta região com outras onde tais parâmetros já foram determinados.
Devido ao excelente ajuste linear obtido no processo numérico para o cálculo dos parâmetros de escala e de forma, pode-se afirmar que o modelo de Weibull foi adequado à distribuição obtida, apresentando um pequeno erro residual (3,2%). Além disto, a sistematização dos métodos utilizados, como a integração trapezoidal e a regressão linear, pode possibilitar a aplicação do presente trabalho para a caracterização do regime eólico de qualquer outra região.
Como existe uma razoável estabilidade no regime eólico da região, devido ao pequeno coeficiente de variação (20%), a implantação de um sistema gerador eólico dimensionado à velocidade média anual do vento obtida (2,77 m s-1) pode não causar grandes oscilações. Além disto, pelo presente trabalho, tal dimensionamento pode ser realizado através da densidade de potência eólica média (24,58 W m-2), que caracteriza a potência média disponível no vento.
Haja vista que vários estudos realizados na Fazenda Experimental são voltados a projetos de implantação de implantação de turbinas eólicas, este parâmetro pode vir a ser uma importante variável para auxílio nas análises de viabilidade econômica, o que também pode ser realizado em qualquer outro local, utilizando os métodos de caracterização analítica do presente trabalho.
Recebido pelo Conselho Editorial em: 13-8-2008
Aprovado pelo Conselho Editorial em: 10-1-2011
Referências bibliográficas
- CASTRO, R.M.G. Introdução à energia eólica Lisboa: Portugal: Universidade Técnica de Lisboa, 2004. 82 p. (Série Energias Renováveis e Produção Descentralizada).
- GABRIEL FILHO, L.R.A. Análise e modelagem geométrica da potência gerada por um sistema híbrido solar fotovoltaico eólico 2007. 136 f. Tese (Doutorado em Agronomia) - Universidade Estadual Paulista, Faculdade de Ciências Agrárias, Botucatu, 2007.
- GABRIEL FILHO, L.R.A.; SERAPHIM, O.J.; CREMASCO, C.P.; CANEPPELE, F. de L. Metodologia da determinação dos parâmetros característicos de sistemas eólicos de geração de energia. Revista Technologia, Canoas, v.9, p.15-27, 2008.
- HASSAN, U.; SYKES, D.M. Wind structure and statistics In: FRERIS, L.L. (Ed.). Wind energy conversion systems New York: Prentice Hall, 1990. p.11-32.
- KOLLING, E. M.; SOUZA, S. N. M. de; RICIERI , R. P.; SAMPAIO, S. C.; DALLACORT, R. Análise operacional de um sistema fotovoltaico de bombeamento de água. Engenharia Agrícola, Jaboticabal, v. 24, n. 3,p. 527-535, 2004.
- MARINI, J.A.; ROSSI, L.A. Sistematização do dimensionamento técnico e econômico de sistemas fotovoltaicos isolados por meio de programa computacional. Engenharia Agrícola, Jaboticabal, v.25, n.1, p.67-75, 2005.
- SILVA, B.B. da; ALVES, J.J.A.; CAVALCANTI, E.P.; DANTAS, R.T. Potencial eólico na direção predominante do vento no Nordeste brasileiro. Revista Brasileira de Engenharia Agrícola e Ambiental, Campina Grande, v.6, n.3, p.431-439, 2002.
- WEIBULL, W. A statistical distribution function of wide applicability. Journal of Applied Mechanics, New York, v.18, n.3, p.293-297, 1951.
Datas de Publicação
-
Publicação nesta coleção
16 Mar 2011 -
Data do Fascículo
Fev 2011
Histórico
-
Recebido
13 Ago 2008 -
Aceito
10 Jan 2011

 Caracterização analítica e geométrica da metodologia geral de determinação de distribuições de Weibull para o regime eólico e suas aplicações
Caracterização analítica e geométrica da metodologia geral de determinação de distribuições de Weibull para o regime eólico e suas aplicações