Abstracts
This paper analyzes the order of integration of the consumption-income ratio in 10 South American countries. To do this, the individual ADF test, its panel versions and theMinimumLMunit root test with structural break(s) were employed. While the former tests found more favorable evidence of an integrated process, after controlling for structural breaks only Uruguay seems to be integrated. Thus, in general, the consumption-income ratio was diagnosed as a stationary process, as suggested by the relative income hypothesis, the habit persistence model, the permanent income hypothesis and the life cycle hypothesis.
Consumption-income ratio; unit root tests; structural break; South America
Este artigo analisa a ordem de integração da razão consumo-renda em 10 países da América do Sul. Para tanto, utilizamos o teste ADF e sua versão painel, além de um teste LM de raiz unitária com quebra estrutural(s). Enquanto os primeiros testes encontraram evidências mais favoráveis a processos integrados, após o controle de quebras estruturais apenas o processo do Uruguai parece ser integrado. Assim, em geral, a razão consumo-renda foi diagnosticada como um processo estacionário, como sugerido pelo modelo de hábito e pelas hipóteses de renda relativa, renda permanente e ciclo de vida.
ARTICLES
The stationarity of consumption-income ratios: evidence from South American countries
Fábio Augusto Reis GomesI; Douglas de Souza FranchiniII
IInsper Instituto de Ensino e Pesquisa. Address: Rua Quatá, 300, Sala 422, Vila Olímpia. São Paulo, SP, Brazil. CEP: 04546-042. Email: FabioARG@isp.edu.br
IIInsper Instituto de Ensino e Pesquisa
RESUMO
This paper analyzes the order of integration of the consumption-income ratio in 10 South American countries. To do this, the individual ADF test, its panel versions and theMinimumLMunit root test with structural break(s) were employed. While the former tests found more favorable evidence of an integrated process, after controlling for structural breaks only Uruguay seems to be integrated. Thus, in general, the consumption-income ratio was diagnosed as a stationary process, as suggested by the relative income hypothesis, the habit persistence model, the permanent income hypothesis and the life cycle hypothesis.
Keywords: Consumption-income ratio, unit root tests, structural break, South America
JEL classification: C12, C22, E21.
RESUMO
Este artigo analisa a ordem de integração da razão consumo-renda em 10 países da América do Sul. Para tanto, utilizamos o teste ADF e sua versão painel, além de um teste LM de raiz unitária com quebra estrutural(s). Enquanto os primeiros testes encontraram evidências mais favoráveis a processos integrados, após o controle de quebras estruturais apenas o processo do Uruguai parece ser integrado. Assim, em geral, a razão consumo-renda foi diagnosticada como um processo estacionário, como sugerido pelo modelo de hábito e pelas hipóteses de renda relativa, renda permanente e ciclo de vida.
1 Introduction
The time series properties of the consumption-income ratio or the average propensity to consume hereafter APC - are a controversial issue on theoretical grounds. The Keynesian absolute income hypothesis, the Marxian underconsumption theory, and Deaton's (1977) involuntary savings theory imply an integrated APC. The relative income hypothesis, the habit persistence model, the permanent income hypothesis and the life cycle hypothesis lead to a stationary APC. An integrated behavior means that policy shocks are likely to have a permanent effect on the APC. On the other hand, the stationary case implies the existence of a long-run equilibrium relationship between consumption and income, which means both that APC has a mean reversion behavior and shocks have temporary effects.
On empirical grounds, these conflicting predictions that have been evaluated by means of unit root tests and the results are also controversial. Molana (1991), Drobny & Hall (1989) and Hall & Patterson (1992) analyzed the UK case using the Augmented DickeyFuller (ADF) unit root test and their findings indicate that APC is non-stationary. Horioka (1997) reached the same result for Japan, applying the ADF test. Applying the same test, King et al. (1991) reached the opposite conclusion for the US economy. In addition, Ungern-Stemberg's (1986) findings indicated that UK and Germany present a stationary APC.
A feature of these earlier papers is the use of the ADF test to investigate the order of integration of APC. Currently, the ADF problem of low-power is well-known. To overcome it, the following literature has used more powerful tests, like panel and asymmetric unit root tests. Sarantis & Stewart (1999) analyzed 20 OECD countries using panel unit root tests and still obtained non-stationary proceses for all these. Cook (2003) confirmed this result for the UK a country studied by Sarantis & Stewart (1999) , using powerful modifications of the ADF test: the weighted symmetric DickeyFuller test (Park & Fuller (1995)) and the recursive mean adjusted DickeyFuller test (Shin & So (2001)).
Applying recent advances in panel and asymmetric unit root tests, Tsionas & Christopoulos (2002), studied 14 European countries analyzed by Sarantis & Stewart (1999). Initially, the panel unit roots tests supported the hypothesis of a unit root in the APC. However, taking into account the presence of an asymmetric adjustment, it was found that stationarity prevails in at least one regime for each country. Thus, the asymmetric unit root test offers less evidence in favor of the unit root hypothesis. However, Cerrato & Stewart (2008) analyzed 24 OECD and 33 non-OECD countries using nonlinear panel unit root tests and the results suggested that, for both groups, the majority of the series are I(1).
Cook (2005) examined the same sample that Sarantis & Stewart (1999) addressed, applying unit root tests with structural changes and reversed previous findings of non-stationarity, rejecting the unit root hypothesis for all 20 OECD economies. Both works share the same concern about the ADF test: the lack of power could be the reason behind the non-rejection of the unit root null hypothesis. However, while Sarantis & Stewart (1999) attempted to solve the problem using powerful panel tests, Cook (2005) considered the omission of structural breaks as the source of the lower power. Indeed, Perron (1989, 1997) showed that the ADF tests can generate a misclassification of the order of integration of economic series in the presence of structural changes. Finally, while Sarantis & Stewart (1999) did not reject the unit root hypothesis, Cook (2005) did.
As the literature has focused on developed countries, there is a lack of information about underdeveloped ones.1 To fulfill this need, this paper investigates the APC properties of 10 South American economies, using the ADF test as a benchmark and its panel versions from Maddala & Wu (1991) and Choi (2001). Furthermore, the possibility of structural breaks is taken into account by means of the Minimum LM unit root test with one and two structural break(s) as in Lee & Strazicich (1999) and Lee & Strazicich (2003), respectively.
To preview the main findings of the paper, while the individual ADF test and its panel versions found evidence suggesting an integrated APC, after controlling for structural breaks the evidence indicate just the opposite. Indeed, modeling a broken trend, only Uruguay seems to be integrated. Then, apart fromthis country, shocks to the APC seemto be temporary, as suggested by the permanent income and the life cycle hypotheses. These hypotheses are especially important because they embedded an idea presented in virtually all economics model: consumers desire to smooth their consumption path.
The paper is organized as following. The second section presents the econometric methodology and the data set. The third section displays the results. Lastly, the conclusions are summarized.
2 Econometric Methodology
2.1 Unit Root Tests
To examine the APC order of integration, the ADF test is used as a benchmark (Dickey & Fuller 1979). The test equation for each country takes the following form,
where yt is the logarithm of the consumption income ratio. The lags of the dependent variable used to correct serial correlation, the Schwarz information criterion is employed on set k. The maximum value allowed for k is 8.2
In an attempt to increase the power of the ADF test, its panel versions according to Maddala & Wu (1991) and Choi (2001) were employed. Maddala & Wu (1991) used the Fisher's (1932) results to derive a test that combine the p-values from individual ADF tests. Define πi as the p-value from any individual unit root test for cross-section i, i = 1, ..., N. Then, under the null hypothesis of unit root for all N cross-sections, the following asymptotic result is valid
In addition, Choi (2001) demonstrated that:
where Φ-1 is the inverse of the standard normal cumulative distribution function. Thus, based on individual ADF p-values, both panel tests can be conducted. It's worth noting that the null hypothesis of both tests is the presence of unit root for each country while the alternative hypothesis is stationary for some (not necessarily all) of them. Thus, if the null hypothesis is not rejected, it means that it is not possible to reject that all countries present an integrated APC. However, rejection of the null hypothesis does not imply that all countries are characterized by a stationary APC.3
From Perron (1989), it is well known that the ADF unit root test can fail to reject a false unit root due to misspecification of the deterministic trend function. Indeed, Perron (1989, 1997), Zivot & Andrews (1992) and Lumsdaine & Papell (1997) extended the ADF test allowing exogenous/endogenous break(s), in an attempt to circumvent this drawback. However, these efforts were not absolutely successful, once the critical values of their unit root tests were derived assuming no break(s) under the null hypothesis, which leads to a spurious rejection of the null hypothesis when there is a unit root with breaks (Lee & Strazicich 2001, 2003).
Lee & Strazicich (1999, 2003) developed a one-break and two-break minimum LM unit root test, respectively, the properties of wich are unaffected by break(s) under the null hypothesis, avoiding both the spurious rejection and the trend misspecification. Hence, to investigate the order of integration of the APC series the tests from Lee & Strazicich (1999, 2003) are employed. According to the LM (score) principle, a unit root test statistic can be obtained from the regression:4
where
t is a de-trended series such that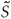 t = yt -
t = yt - 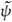 - Zt
- Zt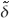 , t = 2, ..., T and Δ
, t = 2, ..., T and Δ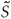 t-i , i = 1, ..., k, terms are included to correct serial correlation. For set k, the general-to-specific approach is used. According to Ng & Perron (1995), k is chosen using the 10% value of the asymptotic normal distribution, 1.645, to evaluate the significance of the last lag. The upper bound for k is 8. Considering 2 changes in level and trend (Model C), the components of
t-i , i = 1, ..., k, terms are included to correct serial correlation. For set k, the general-to-specific approach is used. According to Ng & Perron (1995), k is chosen using the 10% value of the asymptotic normal distribution, 1.645, to evaluate the significance of the last lag. The upper bound for k is 8. Considering 2 changes in level and trend (Model C), the components of 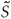 t are: (i) Zt = [1, t, D1t, D2t,
t are: (i) Zt = [1, t, D1t, D2t, 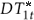 ,
, 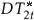 ]' with Djt = 1 for t > TBj + 1, j = 1,2, and zero otherwise;
]' with Djt = 1 for t > TBj + 1, j = 1,2, and zero otherwise; 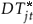 = t for t > TBj + 1, j = 1,2, and zero otherwise; TBj stands for the time period of the breaks; (ii)
= t for t > TBj + 1, j = 1,2, and zero otherwise; TBj stands for the time period of the breaks; (ii) 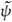 x = y1 - Z1
x = y1 - Z1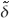 , where y1 and Z1 are the first observations of yt and Zt, respectively; (iii)
, where y1 and Z1 are the first observations of yt and Zt, respectively; (iii) 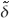 is a vector of coefficients in the regression of Δyt on ΔZt = [1, B1t, B2t, D1t, D2t]', where Bjt = ΔDjt and Djt = Δ
is a vector of coefficients in the regression of Δyt on ΔZt = [1, B1t, B2t, D1t, D2t]', where Bjt = ΔDjt and Djt = Δ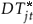 , j = 1,2.
, j = 1,2.
The unit root null hypothesis is described in equation (1) by  = 0 and the test statistic is defined by
= 0 and the test statistic is defined by  , the t-statistic for the null hypothesis
, the t-statistic for the null hypothesis  = 0. To endogenously determine the location of the break points, TBj, a grid search is used to minimize t-test statistic. There is a repeated procedure at each combination of the break points (λj = TBj/T , j = 1,2) over the time interval [.1T, .9T] where T is the sample size. Lastly, the critical values depend on the location of the breaks and are provided for T = 100 by Lee & Strazicich (1999) and Lee & Strazicich (2003) for one-break and two-break tests, respectively.
= 0. To endogenously determine the location of the break points, TBj, a grid search is used to minimize t-test statistic. There is a repeated procedure at each combination of the break points (λj = TBj/T , j = 1,2) over the time interval [.1T, .9T] where T is the sample size. Lastly, the critical values depend on the location of the breaks and are provided for T = 100 by Lee & Strazicich (1999) and Lee & Strazicich (2003) for one-break and two-break tests, respectively.
Following Strazicich et al. (2001) , the relevance of each break date is evaluated using the t-test statistic. If the level (Bjt) and the trend (Djt) dummies are not relevant for one of the break dates, the one-break test is used. If the remaining break is not relevant, the ADF test constitutes an appropriate test, once no structural break was detected.
It is worth noting that, a structural change in APC is compatible with the permanent income and life cycle hypotheses, for instance. An abrupt change in APC occurs when there is a change in income (consumption) that is not followed by a similar change in consumption (income). Indeed, these theories imply that changes in income cause changes in consumption only if permanent income is altered. Thus, if income changes, but permanent income does not vary, then consumption remains constant and, as a result, a structural break in the APC might occur. Also, permanent income can change while the current income is stable and, as a consequence, the APC changes. Therefore, as interpreted by Cook (2005), a stationary APC around a broken trend can be viewed as evidence in favor of the consumption theories mentioned.
2.2 The Data Set
The data set was extracted from Penn World Table 6.2 and refers to the annual income (RGDPL) and the annual ratio of consumption and income (KC), both ranging from 1951 to 2003. The KC refers to the consumption share of RGDPL. Ten South American countries were examined: Argentina, Bolivia, Brazil, Chile, Colombia, Ecuador, Paraguay, Peru, Uruguay and Venezuela. The others South American countries were ignored due to the lack of data over some periods.
Figure 1 displays the APC, consumption and income evolutions for each country. The right axis displays the APC scale while the left axis displays the consumption and income scale. Some countries present an apparent structural break. Most of the breaks appear to have occurred in the 70s when Argentina, Chile, Ecuador, Paraguay, Peru and Uruguay seem to present a negative break while Venezuela seems to have a positive one. In the 80's Bolivia Brazil, Colombia and Venezuela also present a break upon visual inspection. These patterns might be due to common external shocks. In this case, there are three main candidates: the two oils shocks and the debt crisis. In the biennium 1973-74, the Organization of the Petroleum Exporting Countries (OPEC) promoted the first oil embargo, causing a substantial increase in its price which culminated in high inflation across both the developing and the developed world. During the biennium 1978-79, the second oil shock took place, with similar consequences. The debt crisis took place due to both the oil shocks and the tightening US monetary policy that started early in 1980. These events caused large current account deficits in developing countries and a great difficulty for Latin American countries to pay their debts to international creditors that had been financing their development in previous years. The debt crisis began when the international capital markets became aware that Latin American countrieswould not be able to pay back their loans, which occurred in 1982 when Mexico declared default.
In addition to this, internal shocks might also be important. However, unlike external shocks, the internal dynamics of each country are not expected to generate a common pattern among them. For instance, after a negative break around 1985 - which reached its lowest value in Sarney's 1989 external debt moratorium , Brazil's APC seemed to recover it previous pattern in approximately 1994, when the successful Real Stabilization Plan was implemented. Another example is the death of Bolivian President René Barrientos Ortuño in 1969 and the subsequent military coup d'etat in 1971, which suspended its political activities. It can be noted that Bolivia's APC started to decrease around these years.
Ben-David & Loewy (1998) and Ferreira et al. (2009) analyzed the presence of structural breaks in income growth and total factor productivity, respectively. Both works included some Latin American countries and supported the relevance of external shocks - oil shocks and the debt crisis -, as possible sources of the breaks. Following these works, we have analyzed the temporal distribution of the breaks, keeping in mind relevant historical events. However, this exercise can not be viewed as a causality test.
Table 1 presents the descriptive statistics for each country. The mean APC ranges from 0.514 to 0.804, while Venezuela consumes approximately half of its income, and Paraguay needs more than 80% of its income to consume. For comparative purposes, the mean APC during the same period for UK and US are 0.615 and 0.670, respectively. The maximum value is 0.931 from Paraguay in 1994. The minimum value is 0.460, corresponding to Brazil in 1953, one year before the president, Getulio Vargas, committed suicide. The countries with larger standard deviations and coefficients of variation are Peru and Venezuela; indeed they seem to present structural breaks that leverage the dispersion measures. Peru presented an upward trend until mid-1960, when it flattened. Venezuela started a huge increase in the 70s, which stabilized in the early 80s.
3 Empirical Results
The results fromthe ADF test are reported in Table 2. At the 5%level, the unit root null hypothesis is rejected only for Argentina and Paraguay. Increasing the significance level to 10%, Chile and Peru also diverfe from the unit root hypothesis.5 Thus, in general, there are evidences in favor of a non-stationary APC.
The panel versions of ADF test are shown in Table 2. Considering a constant and a linear trend for all countries, Fisher and Choi tests did not reject the unit root null hypothesis for all countries, at the 5% level. Considering only a constant as a deterministic term, the Choi test reached the same conclusion. Thus, the panel tests tend to suggest that APC is an integrated process. The exception was the Fisher test when the linear trend is not included, that the unit root null hypothesis is rejected at the 5% level of significance. If, on the one hand, the panel tests have better power properties, on the other hand, they also are uninformative about which series are stationary when the null hypothesis is rejected. As discussed by Breuer et al. (2001) and Chang et al. (2005), these panel tests are incapable of determining the mixing of I(0) and I(1) series in a panel setting, which constitutes their major disadvantage.
The overall picture suggests that APC is an integrated process, at least, for most countries. However, it is imperative to control for possible structural changes, once its omission leads to a bias in favor of the unit root null hypothesis. This bias is, in general, mainly important for the economies analyzed, given the instability of the South America countries. The results fromthe two-break LMtest are reported in Table 2. First, notice that, based on t-statistic, all countries have at least one dummy relevant at 5%, in each break trend, except for Argentina and Uruguay. This result reflects the importance to control for structural changes for: Bolivia, Brazil, Chile, Colombia, Ecuador, Paraguay, Peru and Venezuela. These 8 countries present a stationary APC, at the 5% level. The significance of the stated LM test statistics is established via comparison with the critical values from Lee & Strazicich (2003).
Argentina and Uruguay cases were re-estimated bymeans of the one-break LM test, as reported in Table 3. For Argentina, only the dummy variable D1 is relevant at the 5% level, and the LM statistic rejected the unit root null hypothesis at the 5% level.6 Uruguay presents an additional difficulty: the dummy variable D1 is significant only at the 10% level. If the break is considered relevant, which seems to be the case based on Figure 2, the LM statistic did not reject the unit root null hypothesis.7 If the break is considered irrelevant, the ADF test can be used and, as noted, this test did not reject the unit root null hypothesis.
Therefore, once structural change is incorporated into the analysis, the APC is found to be stationary for all of the economies considered except Uruguay. Rejection of the unit root hypothesis is emphasized by the relatively short span of data, which might be expected to result in a reduction of the power of the test.
A look at the countries in Figure 2 provides a visual illustration of the estimated broken trend. Figure 2 displays the break points identified by the one/two-break tests reported in Table 1 and Table 2 and plots the logarithm of the APC series and its trend function. The broken trends were estimated via ordinary least squares to connect the break points.
To see the distribution of the break dates, Figure 3 presents a kind of histogram of them. From 32 breaks, 5 occurred in the 1960s; 7 in the 1970s; 4 in the 1980s and 2 in the 1990s. As mentioned, some of them could be attributed to external issues, like the oil shocks, that caused a hike in energy prices. Note that Chile and Ecuador present a break at the beginning of the 70s, while Argentina, Colombia, Paraguay, Peru and Uruguay presented a break in the end of the 70s. Another important external shock was the onset of the debt crisis in 1982. Bolivia, Brazil, Ecuador and Venezuela presented a break close to this year. Thus, in this sense, approximately 60% of the breaks can potentially be attributed to external shocks.
Internal shocks are also able to change the APC pattern. For each country we look for internal events close to the estimated break dates. These events along with the external shocks are listed in Table 4 for interested readers. The analysis of external and internal shocks does not constitute a causality test. However, this attempt to offer possible explanations for breaks that are relevant should be noted because, when there are few observations in a series, the model can over-fit the data, finding breaks that may not exist.
4 Conclusions
To confront contending hypotheses about APC behavior, this paper analyzed its order of integration for 10 South American countries. Whether the consumption-income ratio is mean-reverting or not will affect empirical modeling of consumption functions, our understanding of savings behavior and business cycles, and economic policy. The presence (lack) of mean reversion implies that policy shocks are likely to have transitory (permanent) effects on the APC in South American countries.
First of all, the individual ADF test and the panel versions were employed, finding evidence more favorable to the unit root case. However, the minimum LM unit root break test reverses these results in favor of stationary APC, except in case of Uruguay. Thus, after changes in trend function were properly controlled for, the evidence of mean reversion in nine countries emerged, which is in line with the permanent income and the life cycle hypotheses. In summary, the evidence indicated out that policy shocks are likely to have temporary effects on the South American countries' APC, except in Uruguay.
Bibliography
Recebido em 19 de dezembro de 2008 . Aceito em 05 de maio de 2009.
References
- Ben-David, D. & Loewy, M. (1998), 'Free trade growth and convergence.', Journal of Economic Growth 3, 143170.
- Breuer, B., McNown, R. & Wallace, S. (2001), 'Misleading inferences from panel unit-root tests with an illustration from purchasing power parity.', Review of International Economics 9, 482493.
- Cerrato, M. & Stewart, C. P. C. (2008), Is the consumption-income ratio stationary? evidence from a nonlinear panel unit root test for oecd and nonoecd countries., Technical report, University of Glasgow.
- Chang, T., Lee, K., Nieh, C. & Weibull, C. (2005), 'An empirical note on testing hysteresis in unemployment for ten european countries: panel suradf approach.', Applied Economics Letters 881-12, 881886.
- Choi, I. (2001), 'Unit root tests for panel data.', Journal of International Money and Finance 20, 249272.
- Cook, S. (2003), 'The nonstationarity of the consumption-income ratio: Evidence from more powerful dickeyfuller tests.', Applied Economics Letters 10, 393395.
- Cook, S. (2005), 'The stationarity of consumptionincome ratios: Evidence from minimum lm unit root testing.', Applied Economics Letters 89, 5560.
- Deaton, A. S. (1977), 'Involuntary saving through unanticipated inflation', American Economic Review 6, 899910.
- Dickey, D. & Fuller,W. (1979), 'Distribution of the estimators for autoregressive time series with a unit root.', Journal of the American Statistical Association 74, 427731.
- Drobny, A. & Hall, S. (1989), 'An investigation of the long-run properties of aggregate nondurable consumers' expenditure in the united kingdom.', Economic Journal 99, 454460.
- Ferreira, P., Junior, A. G. & Pessôa, S. (2009), The effects of external and internal shocks on total factor productivity. MIMEO.
- Fisher, R. (1932), Statistical Methods for Research Workers, Edinburgh: Oliver & Boyd.
- Hall, S. & Patterson, K. (1992), 'A systems approach to the relationship between consumption and wealth.', Applied Economics 24, 11651171.
- Horioka, C. (1997), 'A cointegration analysis of the impact of the age structure of the population on the household saving rate in japan', Review of Economic and Statistics 79, 511515.
- King, R., Plosser, C., Stock, J. & Watson, M. (1991), 'Stochastic trends and economic fluctuations.', American Economic Review 81, 819840.
- Lee, J. & Strazicich, M. (1999), Minimum lm unit root test. faculty research paper 9932, department of economics„ Technical report, University of Central Florida.
- Lee, J. & Strazicich, M. (2001), 'Break point estimation and spurious rejections with endogenous unit root tests.', Oxford Bulletin of Economic and Statistics 63, 513615.
- Lee, J. & Strazicich, M. (2003), 'Minimum lm unit root test with two structural breaks.', Review of Economic and Statistics 85, 10821089.
- Lumsdaine, R. & Papell, D. (1997), 'Multiple trend breaks and the unit-root hypothesis.', Review of Economics and Statistics 79, 212218.
- MacKinnon, J. (1996), 'Numerical distribution functions for unit root and cointegration tests.', Journal of Applied Econometrics 11, 601618.
- Maddala, G. & Wu, S. (1991), 'A comparative study of unit root tests with panel data and a new simple test.', Oxford Bulletin of Economic and Statistics 61, 631652.
- Molana, H. (1991), 'The time series consumption function: error correction, random walkand the steady state.', Economic Journal 101, 382403.
- Ng, S. & Perron, P. (1995), 'Unit root tests in arma models with datadependent methods for the selection of the truncation lag.', Journal of the American Statistical Association 90, 269281.
- Park, H. & Fuller, W. (1995), 'Alternative estimators and unit root tests for the autoregressive process.', Journal of Time Series Analysis 16, 415429.
- Perron, P. (1989), 'The great crash, the oil price shock, and the unit root hypothesis.', Econometrica 57, 13611401.
- Perron, P. (1997), 'Further evidence on breaking trend functions in macroeconomic variables.', Journal of Econometrics 80, 355385.
- Sarantis, N. & Stewart, C. (1999), 'Is the consumptionincome ratio stationary? evidence from panel unit root tests.', Economics Letters 64, 309314.
- Shin, D. & So, B. (2001), 'Recursive mean adjustment for unit root tests.', Journal of Time Series Analysis 22, 595612.
- Strazicich, M., Lee, J. & Day, E. (2001), 'Are incomes converging among oecd countries? time series evidence with two structural breaks.', Journal of Macroeconomics 26, 131145.
- Tsionas, E. & Christopoulos, D. (2002), 'Non?sationarity in the consumption? income ratio: Further evidence from panel and assymetric unit root tests', Economics Bulletin 3, 15.
- Ungern-Stemberg, T. (1986), 'Inflation and the consumption function', Review of World Economics (Weltwirtschaftliches Archiv) 122, 741744.
- Zivot, E. & Andrews, D. (1992), 'Further evidence on the great crash, the oil-price shock and the unit root hypothesis.', Journal of Business and Economic Statistics 10, 251270.
Publication Dates
-
Publication in this collection
28 Apr 2010 -
Date of issue
Dec 2009
History
-
Accepted
05 May 2009 -
Received
19 Dec 2008

 The stationarity of consumption-income ratios: evidence from South American countries
The stationarity of consumption-income ratios: evidence from South American countries










