Abstract
Active-Passive Piezoelectric Networks (APPN) integrate active voltage sources with passive resistance-inductance shunt circuits to a piezoelectric patch. This technique allows to simultaneously passively dissipate vibratory energy through the shunt circuit and actively control the structural vibrations. This work presents an analysis of active-passive damping performance of beams with extension and shear APPN. A coupled finite element model with mechanical and electrical degrees of freedom is developed and used to design passive and active control parameters. Then, stochastic modeling and analyses of two cantilever beam configurations, with extension and shear APPN, are performed to evaluate the effect of uncertainties in circuit components on passive and active-passive vibration control. Results show that active-passive shunt circuits can be very interesting since they may combine an adequate passive control performance with an increase of active control authority when a control voltage is applied to the circuit. For the extension configuration, vibration amplitude reductions of up to 22 dB and 28 dB are obtained for passive and active-passive cases, respectively. Considering relative dispersions of 10% for the resistance and inductance values, the passive and active-passive amplitude reductions are found to be in the ranges 16-24 dB and 27-28 dB, respectively. For the shear configuration, increases in the active control authority of up to 29 dB due to a properly tuned resonant circuit are observed. When subjected to uncertainties in the resistance and inductance values, with 10% relative dispersions, the control authority increase is in the range of 6-29 dB.
piezoelectric materials; active-passive piezoelectric networks; vibration control; stochastic modeling; uncertainty analysis
TECHNICAL PAPERS
DYNAMICS, VIBRATIONS AND ACOUSTICS
Structural vibration control using extension and shear active-passive piezoelectric networks including sensitivity to electrical uncertainties
Heinsten F. L. dos SantosI; Marcelo A. TrindadeII
IDepartment of Mechanical Engineering, São Carlos School of Engineering, University of São Paulo, 13566-590 São Carlos, SP, Brazil, hfleal@sc.usp.br
IIDepartment of Mechanical Engineering, São Carlos School of Engineering, University of São Paulo, 13566-590 São Carlos, SP, Brazil, trindade@sc.usp.br
ABSTRACT
Active-Passive Piezoelectric Networks (APPN) integrate active voltage sources with passive resistance-inductance shunt circuits to a piezoelectric patch. This technique allows to simultaneously passively dissipate vibratory energy through the shunt circuit and actively control the structural vibrations. This work presents an analysis of active-passive damping performance of beams with extension and shear APPN. A coupled finite element model with mechanical and electrical degrees of freedom is developed and used to design passive and active control parameters. Then, stochastic modeling and analyses of two cantilever beam configurations, with extension and shear APPN, are performed to evaluate the effect of uncertainties in circuit components on passive and active-passive vibration control. Results show that active-passive shunt circuits can be very interesting since they may combine an adequate passive control performance with an increase of active control authority when a control voltage is applied to the circuit. For the extension configuration, vibration amplitude reductions of up to 22 dB and 28 dB are obtained for passive and active-passive cases, respectively. Considering relative dispersions of 10% for the resistance and inductance values, the passive and active-passive amplitude reductions are found to be in the ranges 16-24 dB and 27-28 dB, respectively. For the shear configuration, increases in the active control authority of up to 29 dB due to a properly tuned resonant circuit are observed. When subjected to uncertainties in the resistance and inductance values, with 10% relative dispersions, the control authority increase is in the range of 6-29 dB.
Keywords: piezoelectric materials, active-passive piezoelectric networks, vibration control, stochastic modeling, uncertainty analysis
Introduction
Due to their strong electromechanical coupling, piezoelectric materials have been widely used as sensors and actuators for structural vibration control. They can be used either as actuators connected to an appropriate control law to provide active vibration control or as sensors connected to shunt circuits to provide passive damping. In the last decade, research was redirected to combined active and passive vibration control techniques. One of these techniques, so-called Active-Passive Piezoelectric Networks (APPN), integrates an active voltage source with a passive resistance-inductance shunt circuit to a piezoelectric sensor/actuator (Tsai and Wang, 1999). In this case, the piezoelectric material serves two purposes. First, the vibration strain energy of the structure can be transferred to the shunt circuit, through the difference of electric potential induced in the piezoelectric material electrodes, and then passively dissipated in the electric components of the shunt circuit (Forward, 1979; Hagood and von Flotow, 1991, Viana and Steffen, 2006). On the other hand, the piezoelectric material may also serve as an actuator for which a control voltage can be applied to actively control the structural vibrations. This active mechanism combined to a velocity feedback, for instance, may then induce an additional active damping in the structure.
There are still some unresolved issues concerning this active-passive damping mechanism, such as for which conditions simultaneous active-passive damping outperforms separate active and passive mechanisms, that is, whether the control voltage should be part of the shunt circuit or not (Thornburgh and Chattopadhyay, 2003). It has been shown that combined active-passive vibration control allows better performance with smaller cost than separate active and passive control, provided the simultaneous action is optimized (Tsai and Wang, 1999). On the other hand, like for purely passive shunted piezoelectric damping, most of the studies concerning APPN focus on the optimization of the electric circuit architecture and components. It is well-known, however, that the performance of both active and passive damping mechanisms is highly dependent on the effective electromechanical coupling provided by the piezoelectric actuators/sensors. Nevertheless, few studies focus on the optimization of this coupling for given structure and piezoelectric material. In particular, it has been shown that piezoelectric actuators using their thickness-shear mode can be more effective than surface-mounted extension piezoelectric actuators for both active (Trindade, Benjeddou and Ohayon, 1999; Raja, Prathap and Sinha, 2002; Baillargeon and Vel, 2005; Trindade and Benjeddou, 2006) and passive (Benjeddou and Ranger-Vieillard, 2004; Benjeddou, 2007; Trindade and Maio, 2008) vibration damping. One of the reasons for that is the thickness-shear electromechanical coupling coefficient k15 that is normally twice the value of the extension one, k31, which may lead to a higher effective electromechanical coupling coefficient (Trindade and Benjeddou, 2009). The thickness-shear mode, originally proposed by Sun and Zhang (1995), can be obtained using longitudinally-poled piezoelectric patches that couple through-thickness electric fields/displacements and shear strains/stresses. On the other hand, although it is well-known that the performance of shunt circuits is quite sensible to the tuning of circuit parameters, little has been published about the complexities in tuning the electric circuit parameters and the effect of the parametric variations on the overall performance of the system (Viana and Steffen, 2006; Andreaus and Porfiri, 2007).
This work presents the modeling of sandwich structures with APPN using extension and thickness-shear piezoelectric sensors/actuators. The model is based on a stress-voltage electromechanical model for the piezoelectric materials fully coupled with the APPN active-passive circuit. To this end, the APPN circuit equations are also included in the variational formulation. Hence, conservation of charge and full electromechanical coupling are guaranteed. The formulation results in a coupled finite element model with mechanical (displacements) and electrical (electrodes charges) degrees of freedom. An analysis of the resulting coupled equations of motion is performed to identify the damping mechanisms provided by an active-passive piezoelectric network. Then, stochastic modeling and analysis of two cantilever beam configurations, with extension and shear piezoceramics, are performed to account for uncertainties in circuit components. This work includes an original modeling and analysis of APPN using shear response mode of piezoelectric materials and also an original sensitivity analysis of passive and active-passive shunted piezoelectric damping using a stochastic model.
Nomenclature
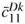
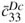
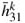
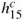
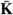
Greek Symbols
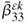
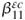
Subscripts
c
e
i
j
L
m
me
n
p
q
Superscripts
c
D
ε
f
k
m
OC
R
RL
SC
Finite Element Model of a Piezoelectric Sandwich Beam
Consider a sandwich beam made of piezoelectric layers and modeled using a classical sandwich theory. Surface layers are made of transversely poled piezoelectric materials, whereas the core layer is made of longitudinally poled piezoelectric materials. Electrodes fully cover the top and bottom skins of all layers so that only through-thickness electric field and displacement are considered. For simplicity, all layers are assumed to be made of orthotropic piezoelectric materials, perfectly bonded and in plane stress state. Bernoulli-Euler theory is retained for the sandwich beam surface layers, while the core is assumed to behave as a Timoshenko beam. The length, width and thickness of the beam are denoted by L, b and h, respectively.
Displacements and strains
The axial and transverse displacement fields of faces and core may be written in the following general form:
where ui is the mid-plane axial displacement of the layer i (i = t for the top layer, i = c for the core layer and i = b for the bottom layer). βi is the cross-section rotation angle and from Bernoulli-Euler assumptions βt = βb = -w', where w' states for ∂w/∂x. zi states for the position of the layer i mid-plane in the global transversal z direction. Using the displacement continuity conditions between layers, the displacement fields may be written in terms of only three main variables, ut, ub and w, so that uc and βc are written as
with hm and hd being the mean and difference of the surface layers thicknesses, ht and hb:
The usual strain-displacement relations for each layer yield the following axial and shear strains for the layer i:
while the remaining strains ε2i, ε3i, ε4i and ε6i vanish. The membrane, bending and shear generalized strains, εim, εif and εic, can be written as
Alternatively, these expressions can be written in terms of the mean and relative axial displacements, instead of the axial displacements of the top and bottom layers, as done in previous works (Benjeddou, Trindade and Ohayon, 1999; Trindade, Benjeddou and Ohayon, 2001).
Piezoelectric constitutive equations
Linear orthotropic piezoelectric materials with material symmetry axes parallel to the beam ones are considered here. The constitutive equations for these materials can be obtained starting from the general expression for the electric enthalpy of a piezoelectric layer
such that
where  , hlj and
, hlj and  (i, j = 1,...,6; l = 1,2,3) denote the elastic (for constant electric displacement), piezoelectric and dielectric (for constant strain) constants of the piezoelectric material, respectively.
(i, j = 1,...,6; l = 1,2,3) denote the elastic (for constant electric displacement), piezoelectric and dielectric (for constant strain) constants of the piezoelectric material, respectively.
For both extension and shear mode piezoelectric layers, only transverse electric field and displacements are considered (D1 = D2 = 0) since the layers have electrodes on top and bottom skins. However, faces and core layers are treated separately, since they have different poling directions. An additional assumption of plane stress state (σ3 = 0) allows to write the following reduced constitutive equations for the faces and the core:
and
where,
Finite element discretization
Lagrange linear shape functions are assumed for the axial displacements, ut and ub, and electric displacements in each layer, D3t, D3c and D3b. For the transverse deflection w, Hermite cubic shape functions are assumed. These assumptions lead to a two node finite element with four mechanical dof and three electrical dof per node. The elementary mechanical degrees of freedom (dof) column vector un is defined as
The axial and transverse displacements of the face layers can be written in terms of the elementary dofs as
where
and
The axial displacement of the core layer uc and the cross-section rotations βi can then be written, using βt = βb = -w' and (2), as
where
According to expressions (5) and (6) for the generalized strains,  ,
,  , and
, and  , they can be written in terms of the elementary dofs as
, they can be written in terms of the elementary dofs as
The membrane, bending and shear strain operators Bmi, Bi and Bcc are defined as
The elementary electric dofs column vector Dn is defined as
Then, the electric displacement in the piezoelectric layers can be written in terms of the elementary dofs
where
Variational formulation
The equation of motions can be written using the Hamilton's principle extended to piezoelectric media
where δTi, δHi and δWm are the virtual variations of kinetic energy Ti and electric enthalpy Hi of layer i and the total virtual work done by mechanical forces on the structure.
The virtual variation of kinetic energy for layer i of the sandwich beam can be written using the displacements fields defined in (1) and supposing that all layers are symmetric with respect to their neutral lines, z = zi, such that integration over the cross-section areas leads to
where ρi is the mass density and Ai and Ii are the area and second moment of area of the cross-section of layer i, respectively, and the dot stands for time derivation.
Using the finite element discretization of generalized displacements (14) and (17),
where Mi is mass matrix of the layer i defined as
The virtual variation of the electric enthalpy Hi for each layer will be composed of mechanical δHmi, electromechanical (piezoelectric) δHmei, and dielectric δHei contributions. In what follows, these are detailed for the faces i = t,b and core i = c layer.
For the core layer, both normal and shear strains contribute to the virtual variation of electric enthalpy, while for the faces only normal strains are relevant. Then, using (4) and supposing symmetric layers, the integration over the cross-section reduces δHmi to
where kc is a shear correction factor for the Timoshenko core layer.
Also supposing symmetric layers and integrating in the cross-section, the piezoelectric contributions to the virtual variation of electric enthalpy can be written as
Notice that the piezoelectric effect couples the transversal electric displacement D3i with membrane and bending strains  and
and  , for the faces, and with shear strain
, for the faces, and with shear strain  , for the core.
, for the core.
The dielectric contribution to the virtual variation of electric enthalpy can be written as
The mechanical, piezoelectric and dielectric contributions to the virtual variation of electric enthalpy can be written in a discrete form substituting the discretized generalized strains (19) and electric displacements (22) in equations (28), (29) and (30), such that
where Kmi are the elastic stiffness matrices of the layer i written as
Kmei states for the electromechanical (piezoelectric) stiffness matrices
and Kei are the dielectric stiffness matrices
The virtual work done by external mechanical forces can be written in terms of a vector of generalized mechanical forces F such that
Replacing the discretized virtual work expressions in the Hamilton's principle (24) and assembling for all finite elements in the structure, the global equations of motion can be expressed as
where u and D are the global mechanical and electric dofs and the mass and stiffness matrices and mechanical force vector were assembled for all layers and all finite elements.
Connecting Piezoelectric Patches to Electrodes and Electric Circuits
To account for the electrodes fully covering the piezoelectric patches top and bottom skins, the electric displacements of selected nodes and layers are set to be equal. This dof assignment can be represented by the following expression:
where Lp is a binary matrix and Dp is a vector of the electric displacement for one piezoelectric patch (constant throughout the electrode surface). Substituting (37) into the variational form of (36), the equations of motion are reduced to
where
In addition, it is supposed that each piezoelectric actuator/sensor can be connected to an electric circuit composed of an inductance Lcj, a resistance Rcj and a voltage source Vcj in series, with j = 1,...,n where n is the number of electric circuits. The equations of motion for the circuits can be written using the Hamilton's principle also as
where δTcj, δWrj and δWej are, respectively, the virtual variation of the kinetic energy due to the inductances Lcj and the virtual work done by the resistances Rcj and voltage sources Vcj connected in series for the j-th electric circuit. These are written as
To account for the connection between piezoelectric patches and electric circuits, it is supposed that electric charges entering a given electric circuit are equal to electric charges of a given piezoelectric patch. Since, due to equipotentiality condition in the electrodes, the electric displacement is constant throughout the electrode surface, the electric charges for a given piezoelectric patch is obtained by multiplying the electric displacement by the electrode area. Thus, a diagonal matrix Ap with elements that are the electrodes areas of each piezoelectric patch is defined. Then, the vector of electric charges generated at the piezoelectric patches and, thus, entering the n electric circuits can be written as
Including the virtual works of (41) in the variational form of the equations of motion (38) leads to
Accounting for the relation between circuits' electric charges and patches' electric displacements (42), the structure-patches-circuits coupled equations of motion can then be written as
where Mq =  LcAp, Cq =
LcAp, Cq =  Rc Ap, Fq =
Rc Ap, Fq =  Vc and a structural damping matrix C can be added a posteriori.
Vc and a structural damping matrix C can be added a posteriori.
Passive and Active Vibration Control Design
From (44), it is possible to observe that the shunt circuit can affect the structural response either passively through coupling of the dynamics of circuit and structure, via the piezoelectric patches, or actively through the application of an electric voltage in the circuit which excites the structure, also via the piezoelectric patches. These effects can be better observed in a frequency response function (FRF) of the structure when subjected to a mechanical or electrical excitation.
For a purely mechanical excitation, such that Vc = 0 and F = b
ejωt, the amplitude of a displacement output y = cu can be written such that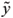 = Gp(ω)
= Gp(ω)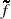 , where the FRF Gp(ω) is
, where the FRF Gp(ω) is
from which it is possible to notice that the resistance and inductance have the effect of changing the dynamic stiffness of the structure. Two particular cases of interest can be derived: i) open-circuit when Cq → ∞ and ii) short-circuit when Mq = Cq = 0, in which cases
As expected, no structural modification is observed in the open-circuit case while, for the short-circuit case, the stiffness of the piezoelectric patches is reduced.
For a purely electric excitation using a single pair patch-circuit, such that F = 0 and Vc =  cejωt, the FRF between the output y and the applied voltage Vc is such that
cejωt, the FRF between the output y and the applied voltage Vc is such that 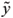 = Gc(ω)
= Gc(ω) c, where
c, where
In this case, the resistance and inductance of the electric circuit have two effects. The first is a modification on the dynamic stiffness of the structure as in the previous case. The second is a modification of amplitude of the equivalent force input induced in the structure by the applied voltage, which for a properly adjusted circuit can lead to a desirable amplification of the control authority of the pair patch-circuit. The particular case of a simple voltage actuator can be derived by making Mq = Cq = 0, for which
Passive vibration control using electromechanical vibration absorbers
Starting from the equations of motion (44) for the case of a single passive electric shunt circuit (RL) connected to a piezoelectric patch embedded in the structure, it is desired to apply the theory of dynamic vibration absorbers for a particular vibration mode of interest. Therefore, the structural response is approximated by the contribution of a single vibration mode of interest such that
where Φn and αn are the vibration mode of interest and its corresponding modal displacement. Thus, neglecting the structural damping, the equations of motion for the resulting two degree of freedom system can be written as
where
MΦn = 1,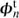 KmΦn =
KmΦn = 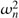 , kp =
, kp = 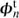 me and bn =
me and bn = 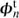 b.
b.
Assuming a mechanical excitation through input , the structural response measured by a displacement output y = cn αn, where cn = cΦn, can be written such that its amplitude is 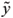 = Gp(ω)
= Gp(ω) 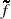 , where the amplitude of the FRF Gp(ω) is
, where the amplitude of the FRF Gp(ω) is
For limited values of cq, |Gp(ω)| has an anti-resonance at a frequency equal to the resonance frequency of the electrical circuit, defined as ωe = (ke/mq)1/2, which can be designed to match the structural resonance of interest ωn. This leads to an expression for mq, and thus for the inductance Lc, in terms of ωn, such that
where Ap is the surface area of the electrode covering the piezoelectric patch connected to the circuit. From the theory of dynamic vibration absorbers, it is known that the anti-resonance is accompanied by two resonances which may have their amplitudes controlled by the electric circuit damping cq. One strategy to design the damping parameter is to minimize the difference between the resonances and anti-resonance amplitudes. This can be done by first using limcq→ 0 |Gp(ω)|2 = limcq→ ∞ |Gp(ω)|2 to find the frequencies for which the amplitude is independent of damping parameter which are
Equalizing the vibration amplitudes at one of these invariant frequencies ω1 and at the anti-resonance frequency ωn leads to an expression for the resistance Rc in terms of the equivalent coupling stiffness kp, electrical stiffness ke, surface area of the electrode Apand structural resonance frequency of interest ωn,
Active vibration control using piezoelectric actuators and state feedback
A state feedback LQR (Linear Quadratic Regulator) optimal control is considered. For that, it is necessary to rewrite the equations of motion (44) in state space form, such that a vector of state variables z is defined, containing the modal displacements and velocities of a series of vibration modes of interest and the electric displacements of the piezoelectric patches and their time-derivatives. This leads to
where
The modal displacements are such that u = Φα and, for mass normalized vibration modes, Ω2 = ΦtKmΦ and Λ = ΦtCΦ. Ω is a diagonal matrix which elements are the undamped natural frequencies of the structure with piezoelectric patches in open-circuit.  =
= 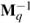
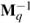 Cq are both diagonal matrices which elements stand, respectively, for the squared natural frequencies of the electric circuits and the ratio between the resistances and inductances (
Cq are both diagonal matrices which elements stand, respectively, for the squared natural frequencies of the electric circuits and the ratio between the resistances and inductances (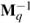 Cq =
Cq = 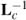 Rc). The electromechanical coupling stiffness matrix projected in the undamped modal basis is defined as Kp = Φtme. Input b and output c distribution vectors are also defined, with modal projections bΦ = Φtb and cΦ = cΦ, and f is a vector of the amplitudes of each mechanical force applied to the structure.
Rc). The electromechanical coupling stiffness matrix projected in the undamped modal basis is defined as Kp = Φtme. Input b and output c distribution vectors are also defined, with modal projections bΦ = Φtb and cΦ = cΦ, and f is a vector of the amplitudes of each mechanical force applied to the structure.
A linear state feedback for the applied voltages Vc is assumed such that Vc = - gz = -gdmα - gdeDp - gvm - gve
- gve
For a single-input mechanical excitation f, the closed-loop or controlled amplitude of a single displacement output y can be written such that 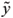 = Gh(ω)
= Gh(ω) 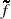 , where the FRF Gh(ω) is
, where the FRF Gh(ω) is
which can also be derived from the second order equations of motion projected into the undamped modal basis leading to
where the closed-loop dynamic stiffness of the electric circuit Dcc is

In this work, the control gain g is calculated using the standard optimal LQR control theory applied to a single-input/single-output case, that is, with only one active-passive patch-circuit pair for the control to minimize the vibration amplitude at one specific location of the structure, such that the following objective function is minimized:
where [y\dot] is the velocity at one location of interest and Vc is the control voltage applied to the active-passive shunt circuit. The weighting factor r is automatically adjusted to guarantee a maximum control voltage of 200 V in all cases following an iterative routine proposed in (Trindade, Benjeddou and Ohayon, 1999).
Results and Discussion
In this section, the FRFs of two cantilever beam configurations, with extension and shear piezoceramics as shown in Figure , are analyzed in order to evaluate the APPN performance in terms of passive damping, control authority and active-passive damping. The extension and shear piezoceramics are made of PZT-5H material whose properties are:  = 97.767 GPa,
= 97.767 GPa,  = 119.71 GPa,
= 119.71 GPa,  = 42.217 GPa, ρ = 7500 kg m-3, piezoelectric coupling constants
= 42.217 GPa, ρ = 7500 kg m-3, piezoelectric coupling constants 31 = -1.3520 109 N C-1 and h15 = 1.1288 109 N C-1, and dielectric constants
 = 57.830 106 m F-1 and
= 57.830 106 m F-1 and  = 66.267 106 m F-1. For the Aluminium beam, material properties are: Young's modulus 70.3 GPa and density 2710 kg m-3 and, for the foam, Young's modulus 35.3 MPa, shear modulus 12.7 MPa and density 32 kg m-3. A viscous damping of 0.5% and a shear correction factor kc = 0.83 were considered.
= 66.267 106 m F-1. For the Aluminium beam, material properties are: Young's modulus 70.3 GPa and density 2710 kg m-3 and, for the foam, Young's modulus 35.3 MPa, shear modulus 12.7 MPa and density 32 kg m-3. A viscous damping of 0.5% and a shear correction factor kc = 0.83 were considered.
First, the beam with extension piezoelectric patch is analyzed. The resistance and inductance were tuned to the first resonance frequency, using the methodology presented in the previous section. Notice, however, that the values obtained using (52) and (54), Rc = 34117 Ω and Lc = 406 H, are just a first approximation to the optimal values and had to be fine-tuned manually to Rc = 31541 Ω and Lc = 390 H. The purely passive action is obtained by eliminating the voltage source and the purely active action is obtained by making Rc = Lc = 0. For the general case, the inductance and resistance not only modify the dynamic stiffness of the structure, leading to damping and/or absorption, but also affects the active control authority of the actuator.
The purely passive performance of resistive and resonant shunt circuits can be evaluated using the frequency response of the beam tip velocity when the beam is subject to a transverse force at the same point (Figure 2). The reference is considered to be unitary. It is possible to observe that both shunt circuits affect significantly only the first resonance, as expected. Figure 3 presents the same response, zoomed at the first resonance, from which one can conclude that both shunt circuits may yield a vibration amplitude reduction but the resonant circuit leads to a much better performance (approximately 22 dB vibration amplitude reduction). The resistive circuit leads to a variation in the resonance frequency, between short-circuit and open-circuit ones, and also induces an equivalent damping factor. For the resonant circuit, tuning of its resistance allows to reduce amplitude at the structure's resonance frequency (i.e. the anti-resonance of the coupled system) at the cost of increasing the amplitude at the two resonance frequencies of the coupled system. Figure shows the effect of increasing and decreasing the resistance of the optimal resonant circuit by 20%.
Figure 5 shows the active control authority of the piezoelectric material, acting as an actuator through the shunt circuit, measured as the beam tip velocity response when subject to a voltage applied to the circuit. As expected, the resistive shunt circuit diminishes the active control authority for all frequencies, since part of the input electric energy is being dissipated through the resistance. On the other hand, the resonant shunt circuit allows an increase of the active control authority around the first resonance at the cost of reducing it for the remaining frequency range.
Then, the LQR state feedback control strategy voltage presented previously was considered to evaluate the control voltage to be applied to the circuit and actively reduce the vibration amplitude of the beam. Figure 6 shows the beam tip mobility, zoomed at the first resonance, for uncontrolled beam (open-circuit, Rc→∞), passive controlled beam with resistive (Rc = 144 kΩ, Lc = 0, Vc = 0) and resonant (Rc = 31541 Ω, Lc = 390 H, Vc = 0) shunt circuits, and active-passive controlled beam with resistive (Rc = 144 kΩ, Lc = 0, Vc < 200 V) and resonant (Rc = 31541 ω, Lc = 390 H, Vc < 200 V) shunt circuits. The active-passive control yields better performance than its passive counterpart with amplitude reductions of approximately 14 dB (resistive) and 28 dB (resonant). Therefore, despite the small reduction on active control authority at the resonance frequency, active-passive control always outperforms the corresponding passive one.
Then, a similar analysis was performed for the sandwich beam with embedded shear piezoelectric patch. In this case, the resistance and inductance values obtained from (18) and (20) are Rc = 835.9 Ω and Lc = 121.7 H and were fine-tuned manually to Rc = 835.8 Ω and Lc = 121.5 H. The purely passive performance of resistive and resonant shunt circuits are presented in Figures 7 and 8. It is possible to observe that the vibration reduction performance is much smaller than in the previous case for both shunt circuits. This is due to the fact the sandwich design considered does not induce significant shear strains in the piezoelectric patch when the beam vibrates on the first mode. For the resonant circuit, the amplitude at structure's first resonance can be further reduced by decreasing the resistance of the circuit as can be seen in Figure 9, which shows the effect of increasing and decreasing the resistance of the optimal resonant circuit by 20%.
Figure 10 shows the active control authority of the shear piezoelectric patch, acting as an actuator through the shunt circuit, measured as the beam tip velocity response when subject to a voltage applied to the circuit. Here, the resistive shunt circuit also leads to a reduction on the active control authority for all frequencies. On the other hand, the resonant shunt circuit yields a very large increase on the active control authority around the first resonance. This fact indicates that, although the passive performance of the shear configuration is not very good, it might be an adequate choice for active or active-passive control since its control authority can be significantly enhanced by the circuit tuning. Indeed, as shown in Figure 11, when applying a similar LQR control strategy to the sandwich beam with shear actuator, the vibration amplitude is greatly reduced as compared to the corresponding passive case. As for the previous case, Figure 11 compares the frequency response of the beam when uncontrolled (open-circuit, Rc→∞), passive controlled with resistive (Rc = 593 kΩ, Lc = 0, Vc = 0) and resonant (Rc = 835.8 Ω, Lc = 121.5 H, Vc = 0) shunt circuits, and active-passive controlled with resistive (Rc = 593 kΩ, Lc = 0, Vc < 200 V) and resonant (Rc = 835.8 Ω, Lc = 121.5 H, Vc < 200 V) shunt circuits. The shear active-passive resonant control leads to an amplitude reduction of approximately 10 dB.
Stochastic Modeling for Uncertainties Analysis
This section presents an approach for analyzing random uncertainties for the resistance R and inductance L elements of the electric shunt circuits. An appropriate probabilistic model for each random variable,  and
and  , is constructed accounting for the available information only, which is the following: (1) the support of the probability density function is ]0,+∞[; (2) the mean values are such that E[R] = R and E[L] = L; and (3) zero is a repulsive value for the positive-valued random variables which is accounted for by the condition E[ln(R)] = cR with |cR| < + ∞ and E[ln(L)] = cL with |cL| < + ∞. Therefore, the Maximum Entropy Principle yields the following Gamma probability density functions for R and L (Soize, 2001; Cataldo et al., 2009; Ritto et al., 2010)
, is constructed accounting for the available information only, which is the following: (1) the support of the probability density function is ]0,+∞[; (2) the mean values are such that E[R] = R and E[L] = L; and (3) zero is a repulsive value for the positive-valued random variables which is accounted for by the condition E[ln(R)] = cR with |cR| < + ∞ and E[ln(L)] = cL with |cL| < + ∞. Therefore, the Maximum Entropy Principle yields the following Gamma probability density functions for R and L (Soize, 2001; Cataldo et al., 2009; Ritto et al., 2010)
and
in which δR = σR/R and δL = σL/L are the relative dispersions of  and
and  and σR and σL are their standard deviations. The Gamma function is defined as Γ(α) =
and σR and σL are their standard deviations. The Gamma function is defined as Γ(α) =  tα-1e-t dt. These probability density functions are shown in Figure together with the histograms of random sets for R and L generated with MATLAB function gamrnd, considering 10000 realizations. The vectors of random realizations for
tα-1e-t dt. These probability density functions are shown in Figure together with the histograms of random sets for R and L generated with MATLAB function gamrnd, considering 10000 realizations. The vectors of random realizations for  and
and  where then combined into pairs of RL parameters, which were then applied to the evaluation of realizations of the FRF Gp(θj,ω), Gc(θj,ω) and Gh(θj,ω) using equations (45), (47) and (58), respectively. To improve the analysis of the sensitiveness of the responses to the circuit parameters, three values were considered for the relative dispersions δR and δL: 5%, 10% and 20%. The mean-square convergence analysis with respect to the independent realizations of random variable
where then combined into pairs of RL parameters, which were then applied to the evaluation of realizations of the FRF Gp(θj,ω), Gc(θj,ω) and Gh(θj,ω) using equations (45), (47) and (58), respectively. To improve the analysis of the sensitiveness of the responses to the circuit parameters, three values were considered for the relative dispersions δR and δL: 5%, 10% and 20%. The mean-square convergence analysis with respect to the independent realizations of random variable  p(ω), denoted by Gp(θj,ω) was carried out considering the function
p(ω), denoted by Gp(θj,ω) was carried out considering the function
where ns is the number of simulations, or the number of RL pairs considered, and  (ω) is the response calculated using the corresponding mean model. Figure shows the mean-square convergence analysis for extension and shear configurations considering δR = δL = 0.10. It is possible to observe that for both cases 3000 simulations are enough to assure convergence. Despite that, the statistical analyses presented in the following sections consider all 10000 simulations performed.
(ω) is the response calculated using the corresponding mean model. Figure shows the mean-square convergence analysis for extension and shear configurations considering δR = δL = 0.10. It is possible to observe that for both cases 3000 simulations are enough to assure convergence. Despite that, the statistical analyses presented in the following sections consider all 10000 simulations performed.
The statistical analyses of the FRF amplitudes were performed using their 10000 realizations at each frequency to calculate the corresponding mean values and 95% confidence intervals. The 95% confidence intervals were evaluated using the 2.5% and 97.5% percentiles of the realizations of FRF amplitudes at each frequency. Figure 14 summarizes the simulation procedure.
Figure 15 shows the FRFs for the extension configuration with OC  and RL shunted
and RL shunted  piezoceramics, where, for last case, the nominal values of R = 31541 Ω and L = 390 H were used. It also shows the mean value (Gp) and 95% confidence intervals
piezoceramics, where, for last case, the nominal values of R = 31541 Ω and L = 390 H were used. It also shows the mean value (Gp) and 95% confidence intervals  of random variable
of random variable  p(ω) for δR = δL = 0.10. Notice that the RL shunt circuit does not affect the FRF but near the first resonance (for which the shunt circuit was designed). In the FRF zoomed near the first resonance (Figure 15), one may notice that the nominal model indicates a reduction in the vibration amplitude of 22 dB (considering the difference between peak responses for OC and RL), while when considering the circuit components uncertainties this reduction is found to be in the range 16-24 dB. It can be also noticed that the difference between the mean and nominal FRFs is almost negligible.
p(ω) for δR = δL = 0.10. Notice that the RL shunt circuit does not affect the FRF but near the first resonance (for which the shunt circuit was designed). In the FRF zoomed near the first resonance (Figure 15), one may notice that the nominal model indicates a reduction in the vibration amplitude of 22 dB (considering the difference between peak responses for OC and RL), while when considering the circuit components uncertainties this reduction is found to be in the range 16-24 dB. It can be also noticed that the difference between the mean and nominal FRFs is almost negligible.
Then, an analysis of the control authority FRFs for the extension configuration with purely active  and RL shunted
and RL shunted  was performed, including its mean (Gc) and 95% confidence intervals
was performed, including its mean (Gc) and 95% confidence intervals  for δR = δL = 0.10. Figure 16 shows that despite the circuit components uncertainties, the control authority is indeed increased near the first resonance at the cost of being significantly reduced for higher frequencies. The active-passive vibration control performance can be observed in Figure 17, which shows the FRFs for the uncontrolled
for δR = δL = 0.10. Figure 16 shows that despite the circuit components uncertainties, the control authority is indeed increased near the first resonance at the cost of being significantly reduced for higher frequencies. The active-passive vibration control performance can be observed in Figure 17, which shows the FRFs for the uncontrolled  and controlled structure
and controlled structure  , including its mean (Gh) and confidence intervals
, including its mean (Gh) and confidence intervals  for δR = δL = 0.10. Comparison with Figure 15 shows that the LQR control combined with the resonant shunt circuit allows to reduce further the vibration amplitude. Indeed, the nominal model indicates a reduction of 27.5 dB, while the confidence intervals indicate a reduction between 27 dB and 28 dB. It is also worthwhile to notice that the active control also shrinks the confidence intervals, compared to the passive case.
for δR = δL = 0.10. Comparison with Figure 15 shows that the LQR control combined with the resonant shunt circuit allows to reduce further the vibration amplitude. Indeed, the nominal model indicates a reduction of 27.5 dB, while the confidence intervals indicate a reduction between 27 dB and 28 dB. It is also worthwhile to notice that the active control also shrinks the confidence intervals, compared to the passive case.
Similar analyses were done for the shear configuration. Hence, Figure 18 shows the FRFs with OC  and RL shunted
and RL shunted  piezoceramics. For the present shear case, the nominal values of R = 835.8 ω and L = 121.5 H were used. Figure 18 also shows the mean value (Gp) and 95% confidence intervals
piezoceramics. For the present shear case, the nominal values of R = 835.8 ω and L = 121.5 H were used. Figure 18 also shows the mean value (Gp) and 95% confidence intervals  for δR = δL = 0.10. In this case, a much smaller vibration amplitude reduction is observed, since the shear configuration is less appropriate to control the first vibration mode. The nominal model indicates a reduction of 3 dB and based on the 95% confidence intervals one could observe a reduction between 0 dB and 3.3 dB. Notice that, for this configuration, the anti-resonance observed in the nominal model is outside the confidence intervals. This is due to the fact that only the nearly perfect combination of optimal resistance and inductance values may lead to such performance. The shear configuration leads to a significant control authority amplification near the first resonance and, differently from the extension configuration, it occurs also at the resonance (Figure 19). This amplification leads to an increase of 29 dB at the resonance, according to the nominal model, and in the range {6-29} dB, according to the 95% confidence intervals. From Figure 20, the vibration amplitude reduction induced by the active-passive control is 10 dB, according to the nominal model, and between 3 dB and 11 dB, according to the 95% confidence intervals.
for δR = δL = 0.10. In this case, a much smaller vibration amplitude reduction is observed, since the shear configuration is less appropriate to control the first vibration mode. The nominal model indicates a reduction of 3 dB and based on the 95% confidence intervals one could observe a reduction between 0 dB and 3.3 dB. Notice that, for this configuration, the anti-resonance observed in the nominal model is outside the confidence intervals. This is due to the fact that only the nearly perfect combination of optimal resistance and inductance values may lead to such performance. The shear configuration leads to a significant control authority amplification near the first resonance and, differently from the extension configuration, it occurs also at the resonance (Figure 19). This amplification leads to an increase of 29 dB at the resonance, according to the nominal model, and in the range {6-29} dB, according to the 95% confidence intervals. From Figure 20, the vibration amplitude reduction induced by the active-passive control is 10 dB, according to the nominal model, and between 3 dB and 11 dB, according to the 95% confidence intervals.
It is also worthwhile to analyse the effect of the relative dispersions of resistance and inductance values on the confidence intervals of the responses of passive and active-passive controlled structures and the control authority of the shunted piezoelectric actuators. Therefore, two additional values for relative dispersions δR and δL were considered: 0.05 and 0.20. It is expected that higher relative dispersions would lead to wider confidence intervals and vice-versa. Figures 21, 22 and 23 show, respectively, the frequency responses Gp, Gc and Gh of the structure with the extension piezoceramics for the two additional relative dispersions. It can be observed in Figure 21, as expected, that the confidence interval is widened (shrunk) compared to the previous case (Figure 15) for larger (smaller) relative dispersions. The range of vibration amplitude reduction (considering the difference between peak responses) becomes 19-24 dB, for 5% relative dispersion, and 11-25 dB, for 20% relative dispersion. The same behaviour was observed for the control authority (Figure 22) and active-passive case (Figure 23). The range of vibration amplitude reduction when using the active-passive shunt circuit remains 27-28 dB, for 5% relative dispersion, and is widened to 24-29 dB, for 20% relative dispersion.
Similar behaviour was also observed in an analysis performed for the shear actuated sandwich beam. The range of vibration amplitude reduction for the beam with shear piezoceramic patch connected to a passive resonant shunt circuit was 0-2.7 dB and 0-3.6 dB for 5% and 20% relative dispersions, respectively (Figure 24). In terms of control authority, as shown in Figure 25, increasing the resistance and inductance relative dispersions yields decreasing lower limit for the confidence intervals, 16 dB and 0 dB for 5% and 20% relative dispersions, respectively, while the upper limit remains unchanged (29 dB). The confidence intervals for the active-passive performance, in terms of vibration amplitude reduction, of the shear actuated piezoceramics are also widened when increasing the corresponding resistance and inductance relative dispersions and vice-versa. The range of vibration amplitude reduction for the active-passive shunted shear piezoceramics is 5-11 dB, for 5% relative dispersion, and 2-11 dB, for 20% relative dispersion.
Concluding Remarks
This work presented an analysis of active-passive damping performance of beams with extension and shear active-passive piezoelectric networks (APPN). For that, a coupled finite element model with mechanical and electrical degrees of freedom was developed and used to design passive and active control parameters. Then, a stochastic modeling and analysis of two cantilever beam configurations, with extension and shear APPN, was performed to evaluate the effect of uncertainties in circuit components on passive and active-passive vibration control. Results have shown that active-passive shunt circuits can be very interesting since they may combine an adequate passive control performance with an increase of the active control authority when a control voltage is applied to the circuit. For the extension configuration, vibration amplitude reductions of up to 22 dB and 28 dB were obtained for the purely passive and active-passive cases, respectively. Considering relative dispersions of 10% for the resistance and inductance values, the passive and active-passive amplitude reductions were found to be in the ranges 16-24 dB and 27-28 dB, respectively. For the shear configuration, increases in the active control authority of up to 29 dB due to a properly tuned resonant circuit were observed. When subjected to uncertainties in the resistance and inductance values, with 10% relative dispersions, the control authority increase was found to be in the range of 6-29 dB.
Acknowledgements
This research was supported by FAPESP and CNPq, through research grants 04/10255-7 and 473105/2004-7, which the authors gratefully acknowledge. The authors also acknowledge the support of the MCT/CNPq/FAPEMIG National Institute of Science and Technology on Smart Structures in Engineering, grant no.574001/2008-5.
Paper received 5 August 2010
Paper accepted 5 February 2011
Technical Editor: Francisco Cunha
References
- Andreaus, U. and Porfiri, M., 2007, ''Effect of electrical uncertainties on resonant piezoelectric shunting,'' Journal of Intelligent Material Systems and Structures, Vol. 18, pp. 477-485.
- Baillargeon, B.P. and Vel, S.S., 2005, ''Active vibration suppression of sandwich beams using piezoelectric shear actuators: experiments and numerical simulations,'' Journal of Intelligent Materials Systems and Structures, Vol. 16, No. 6, pp. 517-530.
- Benjeddou, A., 2007, ''Shear-mode piezoceramic advanced materials and structures: a state of the art,'' Mechanics of Advanced Materials and Structures, Vol. 14, No. 4, pp. 263-275.
- Benjeddou, A. and Ranger-Vieillard, J.-A., 2004, ''Passive vibration damping using shunted shear-mode piezoceramics,'' In Topping, B.H.V. and Mota Soares, C.A., eds., Proceedings of the Seventh International Conference on Computational Structures Technology, Civil-Comp Press, Stirling, Scotland, p. 4.
- Benjeddou, A., Trindade, M.A., and Ohayon, R., 1999, ''New shear actuated smart structure beam finite element,'' AIAA Journal, Vol. 37, No. 3, pp. 378-383.
- Cataldo, E., Soize, C., Sampaio, R. and Desceliers, C., 2009, ''Probabilistics modeling of a nonlinear dynamical system used for producing voice,'' Computational Mechanics, Vol. 43, pp. 265-275
- Forward, R., 1979, ''Electronic damping of vibrations in optical structures,'' Applied Optics, Vol. 18, No. 5, pp. 690-697.
- Hagood, N.W. and von Flotow, A., 1991, ''Damping of structural vibrations with piezoelectric materials and passive electrical networks,'' Journal of Sound and Vibration, Vol. 146, No. 2, pp. 243-268.
- Raja, S., Prathap, G., and Sinha, P.K., 2002, ''Active vibration control of composite sandwich beams with piezoelectric extension-bending and shear actuators,'' Smart Materials and Structures, Vol. 11, No. 1, pp. 63-71.
- Ritto, T., Soize, C., Sampaio, R., 2010, ''Stochastic dynamics of a drill-string with uncertain weight-on-hook,'' Journal of the Brazilian Society of Mechanical Sciences and Engineering, Vol. 32, No. 3, pp. 250-258.
- Soize, C., 2001, ''Maximum entropy approach for modeling random uncertainties in transient elastodynamics,'' Journal of the Acoustical Society of America, Vol. 109, No. 5, pp. 1979-1996.
- Sun, C.T. and Zhang, X.D., 1995, ''Use of thickness-shear mode in adaptive sandwich structures,'' Smart Materials and Structures, Vol. 4, No. 3, pp. 202-206.
- Thornburgh, R.P., and Chattopadhyay, A., 2003, ''Modeling and optimization of passively damped adaptive composite structures,'' Journal of Intelligent Materials Systems and Structures, Vol. 14, No. 4-5, pp. 247-256.
- Trindade, M.A. and Benjeddou, A., 2006, ''On higher-order modelling of smart beams with embedded shear-mode piezoceramic actuators and sensors,'' Mechanics of Advanced Materials and Structures, Vol. 13, No. 5, pp. 357-369.
- Trindade, M.A. and Benjeddou, A., 2009, ''Effective electromechanical coupling coefficients of piezoelectric adaptive structures: critical evaluation and optimization,'' Mechanics of Advanced Materials and Structures, Vol. 16, No. 3, pp. 210-223.
- Trindade, M.A., Benjeddou, A., and Ohayon, R., 1999, ''Parametric analysis of the vibration control of sandwich beams through shear-based piezoelectric actuation,'' Journal of Intelligent Materials Systems and Structures, Vol. 10, No. 5, pp. 377-385.
- Trindade, M.A., Benjeddou, A., and Ohayon, R., 2001, ''Finite element modeling of hybrid active-passive vibration damping of multilayer piezoelectric sandwich beams - part 2: System analysis,'' International Journal for Numerical Methods in Engineering, Vol. 51, No. 7, pp. 855-864.
- Trindade, M.A. and Maio, C.E.B., 2008, ''Multimodal passive vibration control of sandwich beams with shunted shear piezoelectric materials,'' Smart Materials and Structures, Vol. 17, art. no. 055015.
- Tsai, M.S., and Wang, K.W., 1999, ''On the structural damping characteristics of active piezoelectric actuators with passive shunt,'' Journal of Sound and Vibration, Vol. 221, No.1, pp. 1-22.
- Viana, F.A.C. and Steffen Jr., V., 2006, ''Multimodal vibration damping through piezoelectric patches and optimal resonant shunt circuits,'' Journal of the Brazilian Society of Mechanical Sciences and Engineering, Vol. 28, No. 3, pp. 293-310.
Publication Dates
-
Publication in this collection
06 Dec 2011 -
Date of issue
Sept 2011
History
-
Accepted
05 Feb 2011 -
Received
05 Aug 2010

 Structural vibration control using extension and shear active-passive piezoelectric networks including sensitivity to electrical uncertainties
Structural vibration control using extension and shear active-passive piezoelectric networks including sensitivity to electrical uncertainties























































































