The Effect of Material Property on the Critical Velocity of Randomly Excited Nonlinear Axially Travelling Functionally Graded Plates

Abstract

In this paper, the critical axial speeds of three types of sigmoid, power law and exponential law functionally graded plates for both isotropic and orthotropic cases are obtained via a completely analytic method. The plates are subjected to lateral white noise excitation and show evidence of large deformations. Due to randomness, the conventional deterministic methods fail and a statistical approach must be selected. Here, the probability density function is evaluated analytically for prescribed plates and used to investigate the critical axial velocity of them. Specifically the effect of in-plane forces, mean value of lateral load and the material property on the critical axial speed are studied and discussed for both isotropic and orthotropic functionally graded plates. Since the governing equation is transformed to a non dimensional format, the results can be used for a wide range of plate dimensions. It is shown that the material heterogeneity palys an essential and significant role in increasing or decreasing the critical speed of both isotropic and orthotropic functionally graded plates.

Keywords:
Functionally graded plates; Probability density function; axially moving plate; stochastic vibration; dynamic instability; FPK method

1 INTRODUCTION

During the manufacturing process, many industrial plates move axially along their production and assembly lines. Also, many engineering devices, such as band saws, serpentine belts, moving rolled metal sheets, plastic films, magnetic tapes, paper sheets, textile fibers, etc. can be classified under the subject of axially moving plates. Therefore, obtaining plate's critical axial velocity is the most important step in design of such applications. Low travelling speed decreases the total effectiveness while extra ordinary speed may intensify the transverse vibration and consequently the dynamic instability of plates.

In literature and due to above listed industrial activities, the linear and nonlinear dynamic behaviors of axially moving plates have been studied during two past decades (Hatami et al. 2009) (Pakdemirli and Batan 1993) and (Pakdemirli et al. 1994) investigated the stability of an axially accelerating string numerically. (Fung et al. 1997) studied the transient vibrations of an axially moving viscoelastic string. (Chen et al. 2003) and (Chen et al. 2004a, 2004b) studied the chaos and bifurcation of axially moving viscoelastic strings with different constitutive relations under different excitations numerically. (Zhang 2008) studied the dynamic analysis of an axially moving viscoelastic string using translating string Eigen-functions. (Hatami et al. 2007, 2009) considered prescribed above problems for 2D plates. Recently, (Ghayesh et al. 2012, 2013), (Yang et al 2012), and (Saksa 2012) studied the dynamic stability of elastic and viscoelastic plates under deterministic loads.

In many industrial applications, especially when the moving plate passes through a cooling fluid, the resultant distributed lateral force due to solid structure interaction displays random behavior (Asnafi, 2011). Therefore, the stochastic and statistical approaches must be considered also.

Having good strength and low deformation at high temperatures in many practical problems, leads the researchers use of other materials such as composite and functionally graded materials. Research on the stability analysis of composite and functionally graded plates in the past decade has been noticed. For example, (Chen et al. 2013) studied the dynamic instability of functionally graded material (FGM) plates under an arbitrary periodic load. (Chen and Yang 1990) studied the dynamic stability of laminated composite plates due to periodic in-plane loads. A complete study on the dynamic stability of isotropic FG plates under random lateral loads with some analogical comparisons was done by (Asnafi and Abedi 2015). Of course, the behavior of axially moving functionally graded plates has been less considered in literature. (Piovan and Rubens 2008) studied the vibrations of axially moving flexible beams made of functionally graded materials. (Cardona et al. 2006) investigated the dynamics of axially moving beam made of functionally graded materials.

Considering random parameters in the behavior investigation of axially moving strips, beams or plates, numerically or analytically, for homogenous or non-homogenous plates has been less studied.

In this paper, first the general governing equation for the isotropic and orthotropic sigmoid, power law and exponential type axially moving functionally graded plates under lateral stochastic load in presence of large deformation is derived. After that, this complicated equation is transformed to a non-dimensional format such that the investigation becomes applicable and workable for a wide range of plates. Next, via an analytic approach, the probability density of non-dimensional deflection is derived for further analysis. This is because in stochastic equations, all statistical properties can be obtained via this density. The qualitative changes and instabilities of derived probability density function let somebody see how and when the critical speed happens; also which parameters may intensify or pull it down.

2 FORMULATION OF THE PROBLEM

2.1 Material gradient of isotropic and orthotropic Functionally Graded Plates

Generally, a functionally graded material can be defined by the variation in the volume fraction of its constituents. Famous volume fraction profiles are: power-law, sigmoid and exponential functions (P, S and E-FGM; see (Lanhe et al. 2007) for more details). Figure 1 shows an orthotropic FG plate, and Figure 2 the variation of the material via the thickness for mentioned material profiles.

Figure. 1
A typical axially moving functionally graded plate

Figure. 2
The variation of material property in a: P-FG, b: S-FG and c: E-FG materials.

With reference to these figures, the variation of the material property (p), such as Young's modulus in the x and y-direction (E_x, E_y), density ((), Poisson's ratio ((_xy) and shear modulus (G_xy), is considered to be varying from the upper to the lower surface of the plate throughout its thickness for P, S and E-FGM as (Chi and Chung, 2006):

where n_p, p₁ and p₂ are the material parameter, material property of the lowest (z=h/2) and highest (z=-h/2) surfaces of an orthotropic FGM plate, respectively.

The variation of material property in the thickness direction of the P, S and E-FGM plate are drawn in Fig. 2.

2.2 Governing Equation of Axially Moving Functionally Graded Plates

The governing equation of an isotropic plate can be obtained as a special case of a general orthotropic one; so here, we try to derive the relations for a general orthotropic functionally graded plate. Relative to schematic plate of Fig. 1, consider a simply supported linearly-elastic medium-thick rectangular axially moving orthotropic FG plate with length a, width b and uniform thickness h. Here x and y are the Cartesian coordinates of the mid-surface of the un-deformed plate while z is the coordinate along the thickness direction. If the displacement along x, y and z are u, v and w respectively, the displacement field becomes (Timoshenko et al . 1959):

where u₀(x, y), v₀( x, y) and w₀(x, y) are the displacements at the middle surface. Under the assumption of large deformation, the strain field of the orthotropic FGM plate becomes:

where

For the case of plane stress, the stress-strain relation, in-plane axial forces (N) and the bending moments (M) become:

where

, and are the constant in-plane axial forces which are independent from time and geometry and the matrices A, B, C and D relate to the material properties of the orthotropic FGM plate with such the following equations (Timoshenko et al . 1959):

Now, the equilibrium and compatibility equations in the case of large deformation become:

where q_z is the distributed lateral load. If the plate is subjected only to the transverse load q_z, the in-plane forces can be expressed in term of a stress function ((x, y) which is defined as (Timoshenko et al . 1959):

Consequently, the strains and the bending moment at the middle surface are expressed in term of the stress function ((x, y) and the deflection as:

where

In order to find the relations between the stress function ((x, y) and deflection w, one can substitute Eq. 12 into Eq. 10, and then Eqs. 11 and 13 into 9, including the inertial and linear damping forces and the components of acceleration due to axial moving also, to reach:

where U is the axial velocity and I₁ is defined as:

Eqs. 15 and 16 are general nonlinear partial differential equations; we try to solve them via one of the famous approximate methods known as the Galerkin's method.

2.3 Galerkin's Method

One of the best methods used to solve the partial differential equation of the continuous vibratory system is the Galerkin's method (see (Rao 2010) for more details). Here, the deflection w can be written by series of eigen-functions as:

For the first vibration mode of simply supported plates, the deflection w can be expressed as (Rao 2010):

By substituting Eq. 19 in Eq. 15, one can reach:

The particular solution of Eq. 20 can be easily obtained while its homogeneous solution must satisfy Eq. 11 also. Using some calculation, the following relation for ((x, y) can be achieved:

where the three last terms are attained from the homogeneous solution. Substituting Eqs. 19 and 21 in Eq. 17 and using the properties of orthogonal functions, one can recognize that:

where

These parameters are derived for a general 2D orthotropic axially moving functionally graded plate in presence of large deformations. In the case of isotropic one, using E_x=E_y=2G_xy(1+(_xy) in Eq. 23, we have:

3 DERIVING THE PROBABILITY DENSITY FUNCTION USING FOKKER PLANCK KOLMOGOROV EQUATION

There are various methods to analyze random differential equations, for example, statistical linearization, perturbation methods, using statistical moments, Monte-Carlo simulation, etc. One of the best and more applicable of them in the sense of being analytic is the Fokker-Planck-Kolmlgorov (FPK) method (Bolotin 1984, Potapov 1999, Roberts and Spannos 1990, Fuller 1969). The application of the FPK equation to compute stationary or non-stationary probability density function for nonlinear stochastic oscillators has been found in literature since 1980 decade. See for example (Asnafi and Mahzoon 2005, Cai and Lin 1988, Caughey anf Fai 1982, Yong and Lin 1987). To obtain instability conditions in axially moving plates, this method has been less considered and addressed in literature. As an example, in (Asnafi, 2011), the critical speed of an axially moving elastic plate that is submerged in a fluid with random pressure was obtained using FPK equation.

Generally, the FPK equation in non-stationary format does not present a closed form solution while in stationary cases and under certain conditions (see (Cai and Lin 1988, Yong and Lin 1987) for these conditions), gives an exact probability density function. It was shown in the literature (Asnafi and Mahzoon 2005, Cai and Lin 1988, Yong and Lin 1987) that under such conditions, the typical following randomly excited oscillator:

where G is a general nonlinear function of X and ((t) is the unit white noise excitation, the joint stationary probability density function has the following solution in closed form:

where k is the intensity of the white noise excitation and ( is the normalization factor. For Eq. 22, we assume a general lateral white noise excitation in the following form:

where ((t) is a white noise excitation, whose intensity is k and varies about a mean value q. Now, assuming x₁ and x₂ instead of the W and dW/dt₁ (state variables defined in Eq. 22) and making an analogy between Eqs. 22, 26 and 27, one can easily arrive at the relation in Eq. 29, along with Eq. 30, which shows the joint probability density function of the response in phase plane:

where

The function ( that was also known in the literature as the probability potential is the total mechanical energy of the oscillator. Note also that the parameter ( relates to the normalization factor only. Equation 29 shows the distribution of the probability density of the response over the phase space. In other words, it can specify how the statistical properties change when the parameters of oscillator are varied. It also gives rich information about the behavior of the system, such as the number of equilibrium points, their instabilities and critical speeds. The probability density function must satisfy the following conditions (Bolotin 1984):

Therefore, the relative minima/maxima of the probability density function play the essential role in studying the instability behavior of the plate. With reference to Eqs. 29 and 30, since x₂ = 0 is the only root on the second state, all the roots of PDF must vary on the x₁ axis. To compute the roots, we have:

Equation 32 gives the extrema of PDF for different parameters. In what follows, using this equation, the dynamic instability and critical speed of some axially travelling plates are studied. Note also that the results obtained in the solved examples can be used for a wide range of plates, because the parameters used in Eq. 32 are all non-dimensional.

4 ANALYTIC EVALUATION, RESULTS AND DISCUSSION

In this section, the critical speeds of two typical plates are obtained and discussed analytically using Eq. 32. This equation reveals the extrema of probability density function that tell us about any possibly instability and bifurcation in the response. Simply, when ( in Eq. 32 reveals one real root, the corresponding probability density of deflection has one extreme point and consequently one peak. It means that the plate oscillates around only one point i.e. its dominant equilibrium point. Once the number of real roots of ( changes, the number of peaks of probability density and consequently the number of equilibrium points vary also that means the instability and bifurcation occur.

The parameters of Eq. 32 are some functions of n_p, q, ( and (. Therefore we try to obtain non dimensional critical speed, (_critical with respect to these variables. Physically, these variables relate to material property, non dimensional mean value of lateral load and the non-dimensional in-plane forces (see Eq. 23).

Note also that, in the case of linear vibration, the parameters ( and ( vanish. Therefore the critical speed for a specific mean lateral load q, depends only to the sign of ( - (². Simply ( = (² gives the condition of critical speed, i.e.

where ( is defined in relation 23 but must be computed for linear plates. In this case, of course, we cannot talk about the bifurcation phenomenon since this subject is expressed for nonlinear systems only.

In what follows, without any loss of generality, the method is applied to both isotropic and orthotropic FG plate. In section 5, the corresponding probability density functions are drawn for some cases. After that in section 6, some of the analytic results obtained by this method are validated by numerical outcomes.

4.1 Critical Speed for an Isotropic Functionally Graded Plate

In this example, the method is applied to an isotropic FG plate subjected to random white noise excitation. The mechanical property and dimension of plate are tabulated in Table 1.

Table 1
The mechanical property and dimension of isotropic FG plate

Dimensions (m)	Surface	E (Gpa)	ρ (kg/m3)	v
1×1×0.02	Lowest (Aluminum, Alloy 2024-T4 (Beer et al. 2006))	73	2800	0.33
Highest ( Structural Steel, ASTM-A36 (Beer et al. 2006))	200	7860	0.3

For E-FG plate, the parameters ( and ( in Eq. 32 are solely evaluated with respect to properties of Table 1. For S and P-FG plates, to evaluate above parameters, the value of n_p must be also specified.

The parameter ( that speaks about the external linear damping is assumed to be 0.4 (Abedi et al. 2014) and the parameter k that demonstrate the intensity of white noise excitation is assumed to be 1 for all cases. Now we try to obtain non dimensional critical speed (, while other parameters, i.e. ( and q which relate to in-plane and lateral forces respectively are varied.

Fig. 3 gives any one an idea about the values of non dimensional critical speed in E-FG and two ingredients with respect to ( and q. Each curve in the figure demonstrates the border of instability. In other words, in each ( and q, one can realize the value of critical speed.

Figure 3
The non dimensional critical speed of a: isotropic E-FG, b: Aluminum and c: steel plate with respect to ( and q

Positive value of (, means tensile in-plane force and vice versa for negative value of this parameter. Theoretically, ( = 0 demonstrate the condition, in which the tensile in-plane force transforms to compressive one. This condition, of course does not happen in axially moving plates since a pre tension is required for moving.

With reference to Fig. 3, it is clear that the critical speeds for different values of ( (in-plane lateral force) are in their minimum values when the mean lateral load is zero. Up or down ward lateral loads improve the stability in an almost similar manner.

To obtain the critical speed for S and P-FG plate, the role of material property, n_p should be considered too. In Figure 4, for different values of ( and q and as a function of n_p, the non dimensional critical speeds are evaluated and depicted which lets somebody see the changing in critical speeds with respect to these parameters. The curves on the figure display instability border that can be used to obtain the critical speed. In fact, some one can recognize the value of critical speed for each n_p, ( and q.

Figure 4
The non dimensional critical speed of isotropic P and S-FG plates with respect to n_p at different values of ( and q.

Based on Fig. 4, the critical speed is completely affected by the variation in material property, n_p. It is clear that the behavior of S and P-FG plates are converse. In other words, for tensile in-plane forces, the larger values of n_p result in smaller values of critical speeds for P-FG plate and vice versa for S-FG plate.

Fig. 4 shows another interesting outcome which demonstrates that larger values of n_p in P-FG plate, can improve stability even for zero or compressive in-plane forces. Left column images of Fig.4 show although the homogenous plate (n_p=0) illustrates instability for compressive in-plane loads, the corresponding P-FG plate becomes stable for largely enough values of n_p. It is noted also that the critical speed for P-FG plate is more influenced due to changing in n_p than the S-FG plate.

Similar to previous figure, it is noted that in the presence of lateral loads, the stability increases for both S and P-FG plates. Relative to Fig.4, for q = +/- 0.3, the critical speed for both plates takes higher value than when the mean lateral load equals to zero.

4.2 Critical Speed for an Orthotropic FG Plate

Now, the method is applied to an orthotropic FG plate subjected to random white noise excitation. The mechanical property and dimension of this plate are tabulated in Table 2.

Table 2:
The mechanical property and dimension of orthotropic FG plate.

Dimensions (m)	Surface	Material	Ex (Gpa)	Ey (Gpa)	Gxy (Gpa)	vxy	(kg/m3)
1×1×0.02	Lowest	Fiber / Epoxy (Goodfellow, 2015; Acpsales, 2014; Rahmani et al., 2014)	70	70	5	0.1	1600
Highest	0% alumina (Dag, 2006)	116.36	90.43	38.21	0.28	3980

Similar to that was previously done in Sec. 4.1, the non dimensional speeds for orthotropic E-FG plate together with its ingredients are drawn in Fig. 5.

Figure 5
The non dimensional critical speed of a: orthotropic E-FG, b: Fiber/Epoxy and c: Alumina plate with respect to ( and q

Again and with reference to Fig. 5, it is clear that the critical speeds for different values of ( are in their lowest values when the mean lateral load is zero. Up or down ward lateral loads improve the stability. Since the Fiber/Epoxy shows more stability with respect to alumina, the down ward mean lateral load improves the stability a bit more that the upward.

In Figure 6, the non dimensional critical speeds are evaluated and depicted for different values of ( and q and as a function of n_p for orthotropic S and P-FG plate which display the changing in critical speeds with respect to these parameters.

Figure 6
The non dimensional critical speed of orthotropic P and S-FG plates with respect to n_p at different values of ( and q

Similar to results taken for isotropic plate in Fig.4, again the critical speed is completely affected by the variation in material property, n_p for orthotropic plates. Also the behavior of S and P-FG plates are converse such that the larger values of n_p in P-FG plate can improve/destroy stability for zero or compressive/tensile in-plane forces and vice versa for S-FG plate.

It is noted also that in the presence of lateral loads, the stability increases for both S and P-FG plates. Here, for q = +/- 0.3, the critical speed for both plates takes higher value than when the mean lateral load equals to zero.

5 THE CORESPONDING PROBABILITY DENSITY FUNCTIONS

In this section, to have a better visual realization, the probability density function of the non-dimensional deflection i.e. the first state variable of Eq. 29, are drawn for some specific cases (see also Eqs. 22 and 30). The probability density of a variable illustrates the possible presence of that random variable in the workspace. Therefore the variation of this function lets somebody see the evolution of demanded variable with respect to prescribed parameters. In figure 7, the PDFs of response with respect to non dimensional speed for isotropic P, S and E-FG plates can be seen.

Figure 7
The Probability density function of non dimensional deflection with respect to non dimensional speed of isotropic plates when n_p=5, (=1 and q=0

With reference to Fig.7, it is clear that the instability and jumping is unavoidable in the probability density of response when the axial speed increases. Making an analogy between figures 3, 4 and present figure plays up the instability occurred in vicinity of (=1. This subject is also validated in next section using a numerical procedure.

Similar to that was done in Fig.7, the probability density function of the response for orthotropic FG plates are depicted In Fig. 8. Here the conditions are all the same used for previous figure except that the materials are replaced by orthotropic materials.

Figure 8
The Probability density function of non dimensional deflection with respect to non dimensional speed of orthotropic plates when n_p=5, (=1 and q=0

Again, it is noted that the instability and jumping happen in the probability density of response as the axial speed increases. Exact location of these instabilities are shown in future figures while the results are validated using a numerical method.

6 NUMERICAL VALIDATION

The results of sections 4 and 5 are all obtained from Eq. 32 that itself is extracted from the exact analytic solution of the FPK equation 27. Since the results (sections 4 and 5) are achieved via a complete analytic procedure and this procedure was previously validated in (Abedi and Asnafi, 2015a, Abedi and Asnafi, 2015b), their accuracy and correctness are acceptable but to ensure about the validity, a direct numerical procedure is also employed. Relative to this method, the bifurcation and jumping in the non dimensional deflection is extracted directly from Eq. 22 for the cases studied in section 5. In Fig. 9 the numeric bifurcation diagram of non dimensional deflection of isotropic P, S and E-FG are imposed on the corresponding PDFs obtained previously in Fig. 7. A simple comparison between figures 3, 4 and 8 affirms that at n_p=5, (=1 and q=0, the non dimensional critical speeds are the same for both analytic and numeric methods.

Figure 9
The numeric bifurcation diagram of non dimensional deflection of isotropic plates (dashed line) which are imposed on corresponding PDFs when n_p=5, (=1 and q=0

Similar to that was done in Fig. 9, the numeric bifurcation diagram for orthotropic plates are imposed on corresponding PDFs and drawn in Fig. 10.

Figure 10
The numeric bifurcation diagram of non dimensional deflection of orthotropic plates (dashed line) which are imposed on corresponding PDFs when n_p=5, (=1 and q=0.

An association between figures 5, 6 and 9 confirms that at n_p=5, (=1 and q=0, the non dimensional critical speeds for orthotropic plates are the same for both analytic and numeric methods.

7 CONCLUSIONS

In this paper, using the Fokker Planck Kolmogorov equation, a general probability density function for a class of nonlinear axially moving functionally graded plates under lateral stochastic loads is obtained analytically. Since all the statistical properties of response can be attained using the probability density function, a comprehensive study on the parameters that can affect on this function is done. Especially, the effects of material property, in-plane forces and mean value of lateral load are investigated and discussed. First it is shown that the more tensile in-plane forces results in bigger critical speed for all types of isotropic and orthotropic plates. The material property, n_p plays significant and contradictory role for each material. In both isotropic and orthotropic sigmoid FG plate, a larger value of n_p increases the critical speed for a plate under tensile in-plane forces and vice versa for compressive ones. In contrast, larger n_p results in smaller critical speed for a plate under tensile in-plane forces and vice versa for compressive ones. It is shown that in all cases, a non zero mean for lateral load reduces the critical speed. In other words, up or down ward mean values of lateral load improves the stability. To have a better visual realization, the probability density functions for some case studies are drawn and then using a direct numerical approach, the analytical results are validated. It noted that the results can be used for a wide range of plates since they reported as some non dimensional parameters.

References

• Abedi, M., A. Asnafi, and K. Karami. (2014) To obtain approximate probability density functions for a class of axially moving viscoelastic plates under external and parametric white noise excitation." Nonlinear Dynamics 78.3: 1717-1727.
• Abedi M, Asnafi A (2015a) Instability and Bifurcation Behavior of Orthotropic S-FGM Plates Under Lateral Stochastic Loads Considering Variation of Material Properties. International Journal of Structural Stability and Dynamics, 1450108.
• Abedi M, Asnafi A (2015b). To reduce the instability region in the nonlinear transverse vibration of randomly excited plates using orthotropic P-FG material. Nonlinear Dynamics, 80(3), 1413-1430.
• Acpsales (2014) available at: https://www.acpsales.com/upload/Mechanical-Properties-of-Carbon-Fiber-Composite-Materials.pdf
  » https://www.acpsales.com/upload/Mechanical-Properties-of-Carbon-Fiber-Composite-Materials.pdf
• Asnafi, A. (2011) Analytic Stationary Nonlinear Behavior Investigation of Axially Moving Elastic Plates Submerged in a Fluid with Random Pressure by Using FPK Method. 1th ISAV 2011, Tehran, Iran (In Persian).
• Asnafi, A., and Abedi, M. (2015). A complete analogical study on the dynamic stability analysis of isotropic functionally graded plates subjected to lateral stochastic loads. Acta Mechanica, 226(7), 2347-2363.
• Asnafi, A., Mahzoon, M. (2005) Using FPK Equation to Analyze Nonlinear Behavior of Some Oscillators under Random Forcing Function. 13th ISME conference, Isfahan, Iran.
• Beer, F. P, Russell, E. and Dewlf, J. T. (2006) Mechanics of Materials, 4th Edition, Mc Graw Hill, New York.
• Bolotin, V.V. (1984) Random Vibrations of Elastic Systems. Martinus Nijhoff Publishers.
• Cai, G.Q., Lin, Y.K. (1988) On Exact Stationary Solutions of Equivalent Nonlinear Stochastic System. Int. J. of Non-Linear Mechanics, 23(4), 315-325.
• Cardona, Alberto, et al. (2006) DYNAMICS OF AXIALLY MOVING BEAMS MADE OF FUNCTIONALLY GRADED MATERIALS. Mecánica Computacional 25: 1735-1749.
• Caughey, T. K., Fai, M. (1982) The exact steady state solution of a class of nonlinear stochastic systems. Int. J. of Nonlinear Mechanics, 17(3), 137-142.
• Chen, C.S., Chen, C.W. and Chen, W.R (2013) Dynamic Stability Characteristics of Functionally Graded Plates under Arbitrary Periodic Loads. International Journal of Structural Stability and Dynamics, 13(6), 98-118.
• Chen, L.W. and Yang, J.Y. (1990) Dynamic stability of laminated composite plates by the finite element method. Computers & Structures, 36(5), 845-851.
• Chen, L.Q., Wu, J., Zu, J.W. (2004) Asymptotic nonlinear behaviors in transverse vibration of an axially accelerating viscoelastic string. Nonlinear Dyn, 35(4), 347-360.
• Chen, L.Q., Wu, J., Zu, J.W. (2004) The chaotic response of the viscoelastic traveling string: an integral constitutive law. Chaos, Solitons & Fractals, 21(2), 349-357.
• Chen, L.Q., Zhang, N.H., Zu, J.W. (2003) The regular and chaotic vibrations of an axially moving viscoelastic string based on 4-order Galerkin truncation. J. Sound and Vibration, 261(4), 764-773.
• Chi, S. H. and Chung, Y. L. (2006). Mechanical behavior of functionally graded material plates under transverse load-Part I: Analysis. International Journal of Solids and Structures, 43(13), 3657-3674.
• Chi, Shyang-Ho, and Yen-Ling Chung. "Mechanical behavior of functionally graded material plates under transverse load-part II: numerical results. International Journal of Solids and Structures 43.13 (2006): 3675-3691.
• Dag, S. (2006) Thermal fracture analysis of orthotropic functionally graded materials using an equivalent domain approach. Eng. Fract. Mech. 73, 2802-2828.
• Fuller, A.T. (1969) Analysis of Nonlinear Stochastic System by Means of the Fokker-Planck Equation. Int. J. of Control, 9(6): 603-655.
• Fung, R.F., Huang, J.S., Chen, Y.C. (1997) The transient amplitude of the viscoelastic travelling string: an integral constitutive law. J. Sound and Vibration, 201, 153-167.
• Ghayesh, M. H., Amabili, M., & Païdoussis, M. P. (2013). Nonlinear dynamics of axially moving plates. Journal of Sound and Vibration, 332(2), 391-406.
• Ghayesh, M. H., Kafiabad, H. A., & Reid, T. (2012). Sub-and super-critical nonlinear dynamics of a harmonically excited axially moving beam. International Journal of Solids and Structures, 49(1), 227-243.
• Goodfellow (2015) available at: http://www.goodfellow.com/E/Carbon-Epoxy-Composite.html
  » http://www.goodfellow.com/E/Carbon-Epoxy-Composite.html
• Hatami, S., Azhari, M., Asnafi, A. (2009) Exact Supercritical vibration of travelling orthotropic plates using dynamic stiffness method. 8th International Congress on Civil Engineering May 11-13, Shiraz University, Shiraz, Iran.
• Hatami, S., Azhari, M., Saadatpour, M. (2007) Free vibration of moving laminated composite plates. Composite Structures, 80, 609-620.
• Lanhe, W., Hongjun, W. and Daobin, W. (2007) Dynamic stability analysis of FGM plates by the moving least squares differential quadrature method. Composite Structures, 77(3): 383-394.
• Pakdemirli M., Batan H.(1993) Dynamic stability of a constantly accelerating string. J. Sound and Vibration, 168(2), 371-378.
• Pakdemirli M., Ulsoy A.G., Ceranoglu A. (1994) Transverse vibration of an axially accelerating string. J. Sound and Vibration, 169(2), 179-196.
• Piovan, Marcelo T., and Rubens Sampaio. (2008) Vibrations of axially moving flexible beams made of functionally graded materials." Thin-Walled Structures 46.2: 112-121.
• Potapov, V.P. (1999) Stability of Stochastic Elastic and Viscoelastic Systems. John Wiley and sons.
• Rahmani H, Mahmoudi S H, Ashori A (2014) Mechanical performance of epoxy/carbon fiber laminated composites. Journal of Reinforced Plastics and Composites, 0731684413518255.
• Rao S S (2010) Mechanical Vibration. New York: Prentice Hall.
• Roberts, J.B., Spannos, P.D. (1990) Random Vibration and Statistical Linearization. John Wiley and sons.
• Saksa, T., Banichuk, N., Jeronen, J., Kurki, M., & Tuovinen, T. (2012). Dynamic analysis for axially moving viscoelastic panels. International Journal of Solids and Structures, 49(23), 3355-3366.
• Timoshenko S and Woinowsky-Krieger S (1959) Theory of plates and shells. New York: McGraw-Hill.
• Yang, X. D., Zhang, W., Chen, L. Q., & Yao, M. H. (2012). Dynamical analysis of axially moving plate by finite difference method. Nonlinear Dynamics, 67(2), 997-1006.
• Yong, Y., Lin, Y.K. (1987) Exact Stationary Response Solution for Second Order Nonlinear System under Parametric and External White Noise Excitations. ASME J. of Applied Mechanics, 54, 414-418.
• Zhang, N. H. (2008) Dynamic analysis of an axially moving viscoelastic string by the Galerkin method using translating string eigenfunctions. Chaos Solitons & Fractals, 35, 291-302.

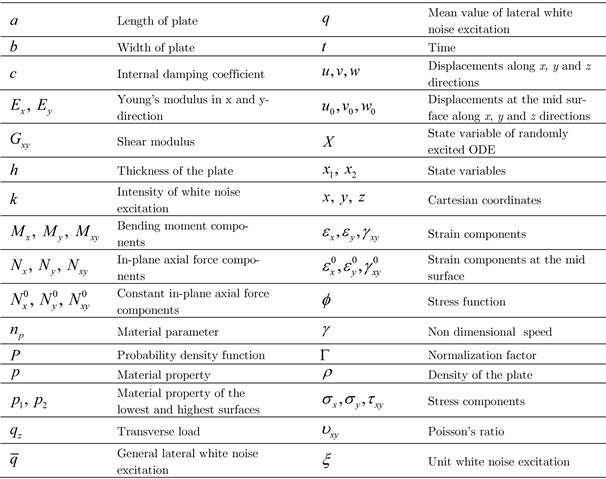
Nomenclature

Publication Dates

• Publication in this collection
  Jan 2016

History

• Received
  20 Jan 2015
• Reviewed
  01 July 2015
• Accepted
  30 Sept 2015