Two theorems by Helmholtz

Two theorems by Helmholtz

H.Fleming

Instituto de Física, Universidade de São Paulo

Recebido em 22/01/2001. Aceito em 21/02/2001

Why isitthat div and curl crop up everywhere in the study of vector fields? These theorems by Helmholtz explain.

Por que os operadores div e rot aparecem em toda parte, no estudo de campos vetoriais? Estes teoremas de Helmholtz explicam.

I Introduction

What is usually called Helmholtz theorem[1] is the fact that a vector field 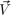which vanishes at infinity is completely determined by giving, everywhere, div 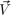and curl 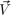. Helmholtz arrived at it in his study of vortices in fluids[4]. Nowadays it is mostly used in Electrodynamics, where the very Maxwell equations express its importance by being nothing else than the specification of what the div and curl of the electric and magnetic fields are.

II The First Theorem

Actually, the Helmholtz theorem¹ proves a slightly different thing, from which the statement above follows immediately: a vector field 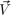which vanishes at the boundaries can be written as the sum of two terms, one of which is irrotational and the other, solenoidal (that is, divergenceless)[2]. Consider the following well-known identity for an arbitrary vector field () :

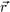If we now take our vector field to be

then it follows that

with

and

Equation(3) is Helmholtz's theorem, as

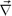
U is irrotational and

×

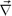
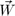
is solenoidal.

But, is it general? It assumes that our vector field can be written as the Laplacian of some other one. This constitutes, however, no problem if 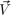vanishes at infinity fast enough, for, then, the equation

which is Poisson's equation, has always the solution

It is now a simple matter to prove, from Eq.(3), that

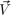
is determined from its

div and

curl. Taking, in fact, the divergence of Eq.(3), we have

which is, again, Poisson's equation, and, so, determines

U as

Take now the

curl of Eq.(3). We have

Now, 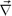. 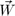= 0, as 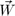= 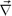× , so another Poisson equation determines 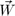. Using U and 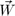so determined in Eq.(3) proves our contention.

III Applications

We start with a very simple one. Consider a homogeneous, ohmian conductor, and let the current density 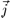vanish at the closed surface which encircles it. We want to inquire as to the possibility that a stationary current may exist in this conductor. We then have 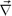. 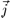= 0, as the current is supposed to be stationary, and 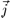= s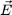, which is Ohm's law. Also, 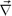× 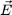= 0, for a static 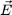. But then,

and so we have both

.

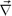
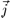
= 0 and

×

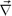
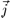
= 0. Besides,

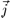
vanishes at the boundaries. It follows, then, from Helmholtz's theorem, that

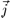
= 0. So, no stationary current can run under these conditions. Notice that this is true also for a torus and its continuous deformations, so that it applies to any closed circuit, proving the necessity that the condition

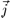
= s

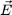
be broken somewhere in the circuit (where the electromotive force is located).

Consider now the electromagnetic potentials. The Maxwell equation

states that there exists a vector field

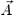
such that

this 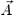being called the vector potential. We may assume that 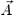vanishes at infinity. Now, what we know about 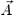is just its curl. Therefore, by Helmholtz's theorem, we are free to choose the value of its divergence. For instance, we may take 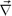. 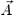= 0, determining completely 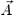. This is the so-called Coulomb gauge. But we can also put 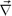. 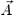= , f being the scalar potential. This is the Lorentz gauge.

IV The Second Theorem

There is another important result by Helmholtz in the same paper we mentioned above. It concerns the most general infinitesimal deformation of a plastic (that is, non-rigid) body.²

Consider a small volume element of a deformable body (a fluid, say). Putting the origin of the coordinates inside this volume element, let 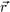be the position of a generic point P. The origin is denoted by O. After a deformation, the material point P has a new position vector, 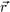+ 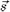. Also the point of the body located at the origin moved, its position now being given by 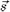₀. We assume, as physically reasonable, that 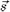is, as a function of position, continuous and differentiable to any order. In what follows, in order to get results of enough generality, we assume P very close to O, that is to say, we consider an infinitesimal volume of the body. Notice that 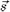itself does have to be small in what follows, though, in considering deformations, this is somewhat academic, as finite deformations can always be obtained from infinitesimal ones (for instance, by Lie group methods). This notwithstanding, the geometrical interpretation we will get is only clear for infinitesimal 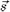. On the other hand, the application for the electric field which is done below would be impoverished by confining 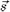to be infinitesimal.

A Taylor expansion for 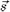gives

neglecting further corrections, what is allowed by the restriction to infinitesimal volume. Here we wrote

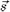
₀ for

(

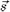
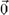
). In more detail, if

s

_i is the i-th component of

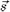
, one has

This can be abbreviated to

or,

where, obviously,

In order to analyse this deformation in terms of more basic ones, let us decompose

T

_li in the following way:

and consider separately the symmetric and the antisymmetric parts. The antisymmetric part is

The symmetric part is

S

_liº

(

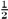
T

_li +

T

_il). It can be decomposed as follows:

where

S º

Tr(

S

_li) =

S

_ii. Now,

S

_li =

(¶

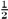
_l

s

_i + ¶

_i

s

_l), so that

We can therefore write Eq.(21) as

where

is a traceless symmetric tensor. Going now to Eq.(17), we can write

or,

where the last term is a vector whose

i-th component is

x

_l

. An object like

S

⁰ is sometimes called a

dyadic.It is a second-order tensor. Let us examine the meaning of the several terms of Eq.(25). The first term of the second member is a translation. The second is an infinitesimal rotation around the axis (

curl

)

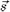
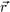
=0, and the remaining terms describe a dilatation of the volume element. To understand them better, let us suppose temporarily that the translation and the rotation vanish, so that we have, for a component of

:

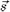
Now,

is a symmetric matrix, so it can be diagonalized. This means that we can change coordinate axes in such a way that, in the new ones, the matrix elements of

S

⁰ have the form

= d

_li

, where no sum is implied in this last expression. So, if the new coordinates are denoted by

X

_i, we have

so that

Consider the infinitesimal "cube" centered at

O, with

P as a vertex. (The "cube" may have curvilinear edges, at least after the deformation). Its volume before the deformation was, in the new coordinates,

V =

X

₁

X

₂

X

₃. After the deformation, it is

V¢ = (

X

₁ +

s

₁)(

X

₂ +

s

₂)(

X

₃ +

s

₃). As we have, considering only the dilatation,

then

and, for the volume,

which, to first order is

that is,

But, as

is traceless,

So, the

do not contribute to the change of volume, but do contribute to the change of the form of the little cube. Referring again to Eq.(25), we see that

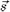
is written as a sum of a translation, plus a rotation, plus an isotropic dilatation, plus a volume-conserving deformation.

³

Notice that Eq.(25) was obtained using only Calculus. So, it should apply to any vector field whatsoever. To shed more light on the role of each term of the expansion, let us use it for the electric field. We then have:

As (

div

)

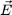
₀ = 4pr(

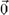
), the second term reads

Now, this is the field of a uniformly charged sphere of radius

r at a point of its surface. It is a radial field to be added to

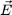
₀.

The second term vanishes if the fields are static. Otherwise,

and

Consider a uniform magnetic field of value

(

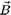
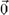
). A vector potential corresponding to it is

so that we have

This means that the third term of Eq.(35) is the contribution of the magnetic field at the origin, treated as follows: extend the value of 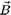at 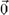to a uniform field. Compute its vector potential and then add the term . All the rest of the field at 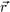(and that could be a lot!) comes from the term S⁰.

V Conclusion

The first Helmholtz theorem explains why the div and curl are so ubiquitous in vector fields. It also explains the structure of Maxwell equations, usually written in such a way that the first member of each is either a div or a curl. The second explains the meanings, and so also the names, of those operators. Considering that Hermann von Helmholtz graduated in Medicine, not in Physics, that was not a bad job at all!

I wish to thank Walter F. Wreszinski for enlightening comments.

²A beautiful treatment of this topic, as well as of the whole vector analysis, is found in Sommerfeld's Mechanics of Deformable Bodies[5].

³This is, in fact, the decomposition, following Weyl[3], of the tensor T_li into its irreducible components under rotations. This corresponds to analysing an infinitesimal deformation in terms of quantities which transform as irreducible representations of the rotation group. In particular, the traceless symmetric tensor "carries" an irreducible representation of dimension 5, an anisotropic object.

• [1] W.K.H. Panofsky and M. Phillips, Classical Electricity and Magnetism, New York, 1970.
• [2] D.H. Kobe, Am. J. Phys. 54, 552(1985).
• [3] H. Weyl, The Classical Groups, Princeton.
• [4] H.v. Helmholtz, Über Integrale der hydrodynamischen Gleichungen, welche den Wirbelbewegungen entsprechen, Crelles J. 55,25(1858).
• [5] A. Sommerfeld, Mechanics of Deformable Bodies New York (1959).
• [6] R. Aldrovandi, J.G. Pereira, An Introduction to Geometrical Physics, World Scientific (1995).

¹

In modern form, much generalized, this is the famous Kodaira-Hodge-De Rham decomposition theorem [6].

Publication Dates

• Publication in this collection
  20 May 2011
• Date of issue
  June 2001

History

• Accepted
  21 Feb 2001
• Received
  22 Jan 2001