Proposal of resilience indices for water mains subject to hydraulic transients and case study in Franca (Brazil)

Proposta de índices de resiliência para adutoras sujeitas a transitórios hidráulicos e caso de estudo em Franca (Brasil)

ABSTRACT

Water main bursts not only lead to financial losses, but also water losses. Climate change and water resources scarcity puts in perspective the need to understand the conditions of the water transportation infrastructure to prevent accidents. The objective of this work is to present resilience indices related to the operation of the water system and infrastructure operational limits to aid decision maker to evaluate risk. The resilience indexes were established based on four indexes arising from transient flows simulation: burst pressure, minimum transient pressure, maximum air volume and resultant forces. Decision making on a complex problem with many parameters based on a simple index is not straightforward, therefore we used a multicriteria decision technique to assist, the simplified three-scale Analytic Hierarchy Process (AHP). To test the proposed method, a case study of a trunk main from the municipality of Franca, Brazil is presented. To calculate the indexes a hydraulic model with transient flows of the referred system was simulated. For the case study, a few scenarios were evaluated. The scenario where no protection devices are present is the most critical.

Keywords:
Analytic hierarchy process; Resilience indices; Transient flows; Water main

RESUMO

Acidentes em adutoras de água, como rompimentos, não só provocam perdas financeiras, como também perdas de água. As mudanças climáticas e a escassez de recursos hídricos colocam como prioridade a necessidade de entender as condições da infraestrutura de transporte de água para prevenir estes prevenir acidentes. O objetivo deste trabalho é apresentar índices de resiliência relacionados com a operação do sistema de água e com os limites operacionais da infraestrutura, para auxiliar os tomadores de decisão na avaliação dos riscos. Os índices de resiliência foram estabelecidos com base em quatro índices decorrentes da simulação do escoamento transitório: pressão máxima, pressão mínima do transitório, volume máximo de ar e máxima força do transitório. A tomada de decisão sobre um problema complexo com muitos parâmetros com base num índice simples não é um processo direto, sendo assim foi utilizada uma técnica de decisão multicritério: o Processo de Analítico Hierárquico (AHP) simplificado de três escalas. Para testar os índices propostos, é apresentado um estudo de caso de uma adutora do município de Franca, Brasil. Para o cálculo dos índices foi simulado o modelo hidráulico do sistema com escoamento transitório. Para o estudo de caso, foram avaliados vários cenários. O cenário sem nenhum dispositivo de proteção ativo é o mais crítico.

Palavras-chave:
Processo analítico hierárquico; Índices de Resiliência; Transitórios hidráulicos; Adutoras

INTRODUCTION

In water distribution systems, trunk water mains are responsible for the transportation of raw water from sources to the water treatment site, and from there to the distribution network. Considering their large diameter and relevance for the distribution system, trunk mains must be carefully designed and built to avoid failures that could lead to water shortage. However, it is not rare to find trunk mains operating on flows greater than the designed, for different reasons. As consequence, the velocity increases and can maximize the effects of transient flows. Transient flows, as opposite to steady-state flows, will consider the velocity variation due to valve maneuver, quick demand changes, filling or emptying of the main, pump start / stop or failure. This change of fluid velocity causes kinematic head to be transformed into pressure head, although, part of it will be converted to acoustic energy and part of it into friction losses (Boulos et al., 2005). Greater the velocity variation, greater the pressure wave intensity that will propagate through the entire system (Crabtree & Oliphant, 2012). Although steady state may be restored after a while, consequences of transient flows can cause severe damage to the infrastructure and surrounding.

Transient flows are common in any hydraulic systems; however, they normally are small, occur gradually and the installation must be designed to endure this pressure. The maximum installation pressure should be determined based on emergency situations, as air valve failure, retention valve failure, hydropneumatics tank failure, pump failure and power failure. Moreover, it is important to predict and verifying the design for extreme events to offer a solution to provide safety measurements and prevent major damages. Extreme transient flow can damage the trunk main as it may cause a peak pressure, vacuum, cavitation, vibration and ultimately water column separation (caused by very low pressure, leading to the formation of vapor cavities that occupy the entire cross-section of the pipe) and pipe rupture (caused by very high pressure). Potential solutions are related to modifying the transient flow, the hydraulic system or the installation of protection mechanism (Boulos et al., 2005). Mathematical models are essential to simulate critical events with different solutions enabling the evaluate of the best protection mechanism (Walski et al., 2003). A few authors have presented works to detect failures or leaks based on hydraulic transients (Zhang & Wan, 2022; Xue et al., 2023; Wan et al., 2021)

Lately, the concept of resilience has been applied to many critical infrastructures systems. Originally introduced to define the ability of an ecosystem to absorb changes whilst maintain the same relationship between populations, this concept evolved and has been used in several areas including engineering (Guo et al., 2021; Yu et al., 2023; Ulusoy et al., 2022). Resilience can be defined as the capacity of the system to adapt to adverse situations whilst continues to develop the function it has been designed for, or even if the system stop functioning, it will restart very quickly (Guo et al., 2021; Klein et al., 2003). For water distribution systems, hydraulic reliability is a way to assess performance. Therefore, hydraulic reliability is the ability of a water distribution system to supply the demand required in adverse circumstances. Greater resilience indicates greater hydraulic reliability. A few authors (D’Ercole et al., 2018; Babayan et al., 2007; Jayaram & Srinivasan, 2008; Kapelan et al., 2005; Todini, 2000) have developed the concept of hydraulic reliability based on resilience. The most applied was presented by Todini (2000) as it measures the capability of the distribution system to overcome failure conditions. However, those concepts are complex for water mains and do not consider the possibility of failure due to dynamic phenomenon.

Resilience of a water distribution system can be measured with indexes that represents the effect of transient flow. The indexes can be applied based on hydraulic reliability and resilience to evaluate how much the trunk main is subject to failure.

However, decisions based on a simple index for a complex problem with different parameters is not always elementary. Hence, a few authors (Kaaviya; Devadas, 2021; Tornyeviadzi et al., 2021; Wang et al., 2020) have combined the concept of index calculation with the concept of Analytic Hierarchy Process (AHP) to evaluate a variety of complex problems. Proposed by Saaty (1980) to solve complex problem with many parameters the AHP method has already been applied in several fields of hydraulic engineering (Feng et al., 2021; Liao et al., 2020; Komolafe et al. 2021; Sutadian et al. 2017; Rajkumar et al., 2022). The process is a multicriteria decision technique effective on decision making. The method contemplates quantitative and qualitative aspects, organizing the critical criterions, for objectives or subjective problems. The scale of comparison ranges from 1-9 varying from “same importance” to “extremely more important”. The method was applied to projects of many different areas like government, health development, engineering, and business. A simplification has been proposed by Li et al. (2015). It is called the three-scale method, used to determine the element of the comparison matrix (A), the proposed scale is shown on Table 1.

Table 1
Three-scale of AHP method.

Numeric rating	AHP scale of importance for comparing pairs	Description
0	$a_i\text{is less importat than}{a}_j$	$a_j\text{has a greater contribution than}{a}_i$
1	Equal importance	$a_{i}and{a}_{j}havethesamecontributionlevel$
2	$a_i\text{is more importat than}{a}_j$	$a_{i}hasagreatercontribution\text{than}{a}_j$

Although the concept of resilience factor and AHP have been applied in some areas related water distribution resilience, to the best of the authors knowledge it has not been applied to evaluate water main resilience to transient flows events. Therefore, the objective of this paper was to develop indexes to replicate the operational conditions of hydraulic infrastructures to aid decision makers to evaluate and compare the risks related to the operation of the system. The proposed method was applied to one trunk water main of the municipality of Franca, Brazil.

CASE STUDY

The municipality of Franca has a population of approximately 335,564 inhabitants and a total of 128,337 water connections. As shown in Figure 1, it is located about 400 km inland from São Paulo city at one of the highest elevations of the state. In the region there are only small rivers with insufficient supply capacity for the city, meaning they need to redraw water from sources far and at lower elevation from consumption points. The method was applied on the trunk main that redraws water from Canoas’s River. This trunk main has a total of 14,706 m and it has two sections of 700 mm diameter, both in ductile iron with section of steel near the two pump stations, which are placed in series. Together the pumps have a capacity of 1,000 l/s, but they operate most of the time at 780 l/s. The total head loss is 430m. The trunk main has 7 one-way tanks (OWT), 5 check valves, 2 anti vacuo valves, 21 air valves and 13 discharge points.

Figure 1
Municipality of Franca located on the map.

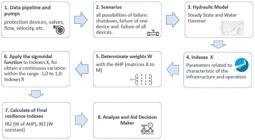
The pump stations (PS-1) and (PS-2) have three pumps each one. The information data is shown in Table 2. The table also presents some characteristics of the protection devices. The flowchart presented in Figure 2 steps of the process.

Table 2
Pump Data and One Way Tanks data.

Pump Data
Device	Distance	Elevation	Power(cv)	Rotational Speed (rpm)	Rotor Diameter (mm)	Inertia (kgm2)
PS-1 (3)	0	710	1350	1750	608	92.4
Booster 1	6740	825.5	600	890	659	45
PS-2 (3)	8240	850	1700	1750	665	117.4
Booster 2	14080	1000	550	890	619	39
One Way Tanks data
Device	Distance	Elevation	Diameter (m)	Loss head coefficient
OWT 1	920	782.2	1 – 1.5	5.85
OWT 2	2760	801.9	1	5.85
OWT 3	6740	825.4	1 – 1.5	5.85
OWT 4	10100	929.4	1	5.85
OWT 5	11940	970.6	1	5.85
OWT 6	12900	997.8	1	5.85
OWT 7	14300	1028.3	1	5.85

Figure 2
Proposed process flowchart.

Scenarios

To assess the pipeline, it is important to evaluate all possibilities of failure, even those with lower probabilities of occurrence, to calculate the stresses limit and provide high reliability. In the case study, multiple scenarios were evaluated, including the total failure of all devices at the same time, in a total of 37 scenarios. To elaborate he scenarios, it was considered a combination of failures of the OWTs, boosters and anti-vacuum valves with the simulation of transient flows from a selection of maneuvers like turning on / off the 3 pumps and booster for each of the two sections of the water main. The elements of the water main are presented on Figure 3. Some specific parameters, such as valve orifice diameters or head loss coefficient in the one-way tanks were estimated based on manufacturers catalogs as shown in Table 2.

Figure 3
Hammer Inputs Elements.

MATERIAL AND METHODS

To evaluate the resilience of trunk water mains normalized indexes were established. The normalized indexes (IR) range from -1 and 1 and are based on the risks classification proposed by (Wang et al., 2014).

Wang et al. (2014) proposed four aspects to describes hydraulic reliability, as presented on Equations 1 to 4, risk related to maximum pressure (1), risk related to minimum pressure and vacuum (2), risk related to maximum vapor volume (3) and risk related to the maximum transient forces (4).

$R_1=\frac{P_{max}-P_b}{P_b}$ (1)

where, $P_{max}$ is the maximum pressure for each node and each pipe for the scenario considered and $P_b$is the maximum design pressure for each node and pipe. In the case of $P_{max}$ <$P_b$; then $R_1<0$, and we must consider $R_1=0$

$R_2=\frac{P_{min}}{P_v}$ (2)

where, $P_{min}$ is the minimum pressure for each node and each pipe for the scenario considered and $P_v$is the vapor pressure. In the case of $P_{min}<0$; then $R_2<0$ and we must consider $R_2=0$

$R_3=\frac{V_{\max i}}{V_{max}}$ (3)

where, $V_{\max i}$ is the maximum vapor volume at nodes and pipes for the scenario i and $V_{max}$ is the maximum vapor volume at nodes or pipes considering all scenarios.

$R_4=\frac{F_{max}-F_b}{F_b}$ (4)

where, $F_{max}$ is the maximum force resultant in each node for the scenarios considered for the transient flows and $F_b$ is the base impact force for each node, estimated to be 25% greater than maximum for calculated for the steady state. If $R_4<\mathrm{0,}{R}_4=0$.

According to Wang et. al. (2014) the resilience index can be determined in two different ways. The first, is based on the maximum risk factor, Equation 5, and the second is based on combining all the factor weighted as Equation 6, with the sum of all weights equal to the unit (Equation 7).

$R=max\left(R_1,R_2\mathrm{,...,}{R}_n\right)$ (5)

where $R$ is the combined risk for a node for $n=3$ or for a pipe for $n=4$, as the risk factor associated with forces generated at the node cannot be applied to pipes.

$R={\displaystyle \sum }_{i=1}^n\left(W_i{R}_i\right)$ (6)

${\displaystyle \sum }_{i=1}^n{W}_i=1$ (7)

where $W_i$ are the weights associated with the risk factor. The weight should vary with pipe material or location of the distribution network.

The risks involve water distribution systems operation based on the structure and on phenomenon of transient flows. Negative index shows lack of resilience and positive values near one denotes elevated resilience conditions. A sigmoidal function was used as it is a continuous function with values between -1 and 1. The resilience was then established based in four indexes arising from transient flows: burst pressure, minimum transient pressure (vapor) established for the trunk main, maximum air volume established for vaporization and resultant forces. All indexes will define the resilience index IR as per Equations 8, 9 and 10.

$I{R}_1=min\left(R_1,R_2,\mathrm{...,}{R}_n\right)$ (8)

$I{R}_2={\displaystyle \sum }_{i=1}^n(W_1{R}_1,W_2{R}_2,\mathrm{...,}{W}_n{R}_n)$ (9)

$I{R}_3=\frac{{{\displaystyle \sum }}_{i=1}^n{R}_i}{4}$ (10)

${\displaystyle \sum }_{i=1}^n{W}_i=1$ (11)

where, $R_i$ is defined by the sigmoidal function:

$R_i=\frac{2}{1+e^{-4x_i}}-1$ (12)

The indexes $x_i$ on Equation 12 are the parameters related to characteristic of the infrastructure and operation of the system and can be determined with Equations 13 to 27.

$x_1=1-\frac{P_{max}}{P_{rup}}$ (13)

$x_2=-\frac{P_{min}}{P_{vapor}}<\mathrm{1,0}$ (14)

$x_3=1-\frac{V_{max}}{V_{pipe}}$ (15)

$x_4=1-\frac{F_{max}}{F_b}$ (16)

where $P_{rup}$ is the rupture pressure according to the supplier catalog or pipe material and thickness, $P_{max}$ is the maximum pressure obtained from the hydraulic simulation for scenario j, $P_{vapor}$ is the vapor pressure of the water, $P_{min}$ is the minimum pressure obtained from the hydraulic simulation for scenario j, $V_{pipe}$ is the volume of a section of the pipe considered on the discretization of the model, $V_{max}$ is the maximum volume of vapor obtained from hydraulic simulation for scenario j, $F_b$ is the resistance force of the pipe considering the thrust blocks, $F_{max}$ is de module of the maximum force obtained on the hydraulic simulation for scenario j for the section analyzed, and finally, $W_i$ are the relative weights regarding the relevance of each device.

Therefore, to determine $x_i$ it is imperative to run a hydraulic model considering the transient flows. In this case, Hammer ® Connect Edition from Bentley® was used. Data for the hydraulic model was made available by the local water company. However, some data had to be calculated, estimated, or extracted from catalogs and books. For instance, $F_b$was estimated, $V_{pipe}$was calculated with Equation 17, $P_{rup}$ was extracted from catalog and $P_{vapor}$ was extracted from a textbook.

$$V_{pipe}=\frac{a\Delta t{D}_i^2\pi }{4}$$ (17)

where a is the celerity of the wave (m/s), $D_i$ pipe internal diameter (m), $\Delta x$ distance travelled by the wave (m), $\Delta t$ time travelled by the wave (s).

The weights were than determined based on the AHP three-scale method as suggested by Li et al. (2015). The process of improved AHP is divided in six steps. The first step consists of defining the goal and factors to establish the hierarchy model. Step two establishes the pairwise comparison matrix A with elements defined according to the tree-scale method. Then, step three develops the judgment matrix B where the elements are defined according to Equation 18.

$b_{i,j}=\left\{\begin{array}{c}1+\left(\frac{r_{max}}{r_{min}}-1\right)\frac{r_i-r_j}{r_{max}-r_{min}},r_i\ge r_j\\ {\left(1+\left(\frac{r_{max}}{r_{min}}-1\right)\frac{r_i-r_j}{r_{max}-r_{min}}\right)}^{-1},r_i<r_j\end{array}\right.$ (18)

For Equation 18 $r_i$, $r_{max}$ and $r_{min}$ are defined per Equations 19, 20 and 21.

$r_i={\displaystyle \sum }_{j=1}^n{a}_{i,j}$ (19)

$r_{max}=max\left\{r_i\right\}$ (20)

$r_{min}=min\left\{r_i\right\}$ (21)

Step four consists in set the antisymmetric matrix C and optimal transfer matrix D with the elements of each matrix determined as per Equations 22 and 23.

$c_{i,j}={\log }_{10}{b}_{i,j}$ (22)

$d_{i,j}=\frac{1}{n}{\displaystyle \sum }_{k=1}^n\left(c_{i,k}-c_{j,k}\right)$ (23)

Step five consists of establishing the quasi-optimal consistent matrix E with terms determined as per Equation 24.

$e_{i,j}={10}^{d_{i,j}}$ (24)

At last, step six will establish the weighting vector solution by using Asymptotic Normalization Coefficient (ANC) as per Equations 25, 26 and 27.

$M_i={\displaystyle \prod }_{k=1}^n{e}_{i,k},\left(i=\mathrm{1,2,}\dots n\right)$ (25)

${\overline{W}}_l=\sqrt[n]{M_i}$(26)

$$W_i=\frac{{\overline{W}}_l}{{{\displaystyle \sum }}_{i=1}^n{\overline{W}}_l}$$ (27)

And finally, the weight vector can be written as Equation 28:

$W={\left(W_1{W}_2\mathrm{...}{W}_n\right)}^T$ (28)

The comparison matrix was created based on the user criterion. The hydraulic modeling was performed using the Hammer ® Connect Edition, which is widely applied in engineering offices and research (Xu et al., 2023; Tawfik, 2023; Hussain et al., 2021).

Hammer ® Connect Edition applies the method of characteristics (MOC) with the theoretical foundations defined in Wylie et al. (1993). The celerity is calculated using the Equation 29.

$c=\frac{\sqrt{\frac{k}{\rho }}}{\sqrt{1+\frac{CkD}{Ee}}}$ (29)

where $c$ is celerity (wave velocity in $m/s$), k is bulk modulus of elasticity (Pa), $\rho$ is the specific mass ($\frac{kg}{m^3}$), E is the Young´s modulus of elasticity for the pipe material, $e$ is the pipe thickness (m) and $C$ is defined by the anchoring condition, Tullis (1989), as a function of Poisson´s ratio.

In the Pump Attributes, “Shut Down after time delay” has been defined as the maneuver that produces the hydraulic transient, along with the instantaneous closing of the check valve downstream of the pump.

To calculate the phenomenon of cavitation, the HAMMER model employs a methodology wherein the volumes of air or vapor concentrated at a specific point along the pipe are represented. This methodology also allows for the calculation of extended air volumes, which occur when air enters the system at a high point in the pipe via an air valve. This latter phenomenon is referred to as the Combination Air Valve (CAV) methodology.

The following information was used for modeling: pipeline records (material, diameter, depth, elevations), topographies, existing protection devices, information about pumping equipment, and operating rules. The nodes used in the modeling correspond to inflection points or points with installed equipment. The initial reservoir in the case study was modeled as a large-dimension reservoir (fixed level). Figure 2 presents a flowchart summarizing the methodology outlined above.

RESULTS AND DISCUSSIONS

Hydraulic modeling results

To calculate the steady state the topologies shown in Figure 3 were inserted into Hammer Connect. The first section starts at pumping station 1 (PS-1) and goes to pumping station 2 (PS-2), while the second section goes from pumping station 2 (PS-2) to the water treatment plant (WTP). An initial result from the model shows the flow in steady state varying between $778l/s$ to $1249l/s$ depending on the scenario.

For modeling the transient flows, a simulation period of 60 seconds was defined. The software selected a time gap of $0.0334s$ for the first section and $0.0282s$ for the second section. Although the small-time gap was not essential, the value suggested by the software was maintained as the computational cost was not a problem in this case. The maximum pressure, minimum pressure, and velocity values correspond to critical values along each section for each scenario, and these values were directly obtained from Hammer software, which was constructed based on real data from Franca. On the other hand, the applied forces were obtained from the model processing. The maneuvers simulated to produce the hydraulic transient are: shutdown of one, two, or three sets of pumps or the booster; starting on all three pumps simultaneously; and shutdown of one or more pumps due to damaged shaft, reducing the inertia of the motor pump set. Table 3 shows the results of the modeling of the hydraulic transients in the different scenarios and indexes x_i determined based on Equations 13 to 16 for all scenarios. The most critical results for each pipe section are shown as it will represent the most adverse conditions that the pipeline can operate.

Table 3
Results transients modeling and indices xi.

No.	Section	Scenario	Pmax (m)	Pmin (m)	Vol max (l)	F (kN)	x1	x2	x3	x4
1	PS1 - PS2	Qop with Booster	183	-7	0	574	0.65	-0.70	1.00	0.33
2	PS1 - PS2	Qop with Booster - Shutdown one pump set	183	-1	0	135.1	0.64	-0.10	1.00	0.33
3	PS1 - PS2	Qop with Booster - Shutdown two pump set	183	-4	0	135.1	0.65	-0.40	1.00	0.33
4	PS1 - PS2	Qop with Booster - Shutdown tree pump set	183	-4	0	135.1	0.65	-0.40	1.00	0.33
5	PS1 - PS2	Qop with Booster - Shutdown Booster	193	-1	0	135.1	0.60	-0.10	1.00	0.33
6	PS1 - PS2	Qop without OWT 1	287	-10	1633.4	1607.9	0.39	-1.00	0.79	-0.22
7	PS1 - PS2	Qop without OWT 2	224	-10	807.4	1130.5	0.54	-1.00	0.94	0.15
8	PS1 - PS2	Qop without OWT 3	235	-10	380.4	1046.9	0.53	-1.00	0.95	0.21
9	PS1 - PS2	Qop without Valve 2	212	-10	41.2	668.2	0.58	-1.00	1.00	0.30
10	PS1 - PS2	Qop without protection devices	386	-10	2684.2	2155.6	0.19	-1.00	0.81	-0.64
11	PS1 - PS2	Qop - shutdown one pump set	191	2	0	135.1	0.62	0.20	1.00	0.33
12	PS1 - PS2	Qop - shutdown two pump set	191	-4	0	135.1	0.62	-0.40	1.00	0.33
13	PS1 - PS2	Qop - shutdown tree pump set	205	-7	0	878.8	0.59	-0.70	1.00	0.33
14	PS1 - PS2	Qop - Starting tree pump set	210	1	0	1250.2	0.55	0.10	1.00	0.22
15	PS1 - PS2	Qop - Damaged shaft	222	-10	32.8	959.8	0.57	-1.00	1.00	0.27
16	PS1 - PS2	Qop - without valves	211	-7	198.1	1585.2	0.58	-0.70	0.97	0.31
17	PS1 - PS2	Q = 1,5 Qop	362	-10	2626.9	1715	0.22	-1.00	0.66	-0.30
18	PS1 - PS2	Q = 1,5 Qop with booster	271	-10	3225.1	1222.8	0.34	-1.00	0.59	0.07
19	PS2 - WTP	Qop with booster	260	-10	65.2	904.6	0.55	-1.00	0.99	0.33
20	PS2 - WTP	Qop with booster - shutdown one pump set	260	-1	0	855.4	0.55	-0.10	1.00	0.33
21	PS2 - WTP	Qop with booster - shutdown two pump set	260	-1	0	854.2	0.55	-0.10	1.00	0.33
22	PS2 - WTP	Qop with booster - shutdown tree pump set	260	-10	65.2	855.8	0.55	-1.00	0.99	0.33
23	PS2 - WTP	Qop with booster - shutdown booster	271	1	0	1012.8	0.53	0.10	1.00	0.28
24	PS2 - WTP	Qop without valves	268	-10	4.7	1296.3	0.53	-1.00	1.00	0.08
25	PS2 - WTP	Qop without OWT 4	268	-10	34.8	877.2	0.53	-1.00	0.99	0.32
26	PS2 - WTP	Qop without OWT 5	268	-10	5	903.6	0.53	-1.00	1.00	0.28
27	PS2 - WTP	Qop without OWT 6	268	-10	43.2	967.5	0.53	-1.00	1.00	0.29
28	PS2 - WTP	Qop without OWT 7	268	-10	7.8	1140.7	0.53	-1.00	1.00	0.28
29	PS2 - WTP	Qop without devices	362	-10	689.6	1545.3	0.12	-1.00	0.94	-0.14
30	PS2 - WTP	Qop without check valve	284	-5	0	1583.8	0.51	-0.50	1.00	0.29
31	PS2 - WTP	Qop - shutdown one pump set	268	0	0	2062.3	0.53	0.00	1.00	0.33
32	PS2 - WTP	Qop - shutdown two pump set	268	0	0	2062.3	0.53	0.00	1.00	0.33
33	PS2 - WTP	Qop - shutdown tree pump set	268	-10	5	2062.3	0.53	-1.00	1.00	0.33
34	PS2 - WTP	Qop - Starting tree pump set	294	-10	0.3	1124.4	0.49	0.00	1.00	0.20
35	PS2 - WTP	Qop - Damaged shaft	283	-10	5.6	1594.6	0.51	-1.00	1.00	0.29
36	PS2 - WTP	Q = 1.5 Qop	308	-10	100.3	1146.4	0.47	-1.00	0.98	0.18
37	PS2 - WTP	Q = 1.5 Qop with booster	298	-10	169.5	1074.2	0.48	-1.00	0.97	0.23

The infrastructure parameters used for calculating the indexes were obtained from catalogs, literature or calculated. The rupture pressure used for steel is $576mH2O$ (Cemil, Tubos e Conexões Ltda, 2023) and for cast iron $K9$ is $410mH2O$ (Saint-Gobain Canalização Ltda, 2017). The vapor pressure at $20°C$ is $-9.8mH2O$ on the relative pressure scale. The volumes of the pipe sections were calculated based on the diameter, celerity, and time gap. The base resistance force $F_b$ was estimated with the base scenario using the project flow $Qo$, shutting down of all three pumps simultaneously and a safety coefficient of 1.5.

Results of the weights according AHP

After determining the indexes for each scenario, the weights were determined according to AHP method proposed by Li et al. (2015). Matrix A, shown on Figure 4, was constructed based on the three-scale method and a decision maker opinion to determine the hierarchy. Matrices B, C, D, E and $M_i$, also shown on Figure 3, were constructed based on Equations 18 to 28. They were then applied to determine the weights ($W_i^T$) vector presented in Equation 30. These weights are than used to calculate the resilience indexes $I{R}_1$, $I{R}_2$ and $I{R}_3$ based on Equations 8 to 11.

Figure 4
Matrices A, B, C, D, E and M_i obtained to determine the weights according to AHP for Franca case study.

$W_i^T=\left\{0.4100.1220.0570.410\right\}$ (30)

The results of applying the AHP indicates that for this case study the decision maker is more concerned with indexes $x_1$ and $x_4$, as the weights for those are higher. Therefore, the decision maker prioritized the maximum pressure and maximum force. These values can change according to the experience of the decision maker and the experience of the operators. Assuming that there is no information that privileges one index over the other, a value equal to the 4 weights can be assigned.

Results of the Partial and Final resilience Indexes

The sigmoidal function, Equation 12, was applied to the indexes $x_i$ of the Table 3 to obtain the partial resilience indices $R_i$ shown in Table 4. The sigmoidal function was applied to obtain a continuous variation within the range -1 to 1. Then, the final resilience index $I{R}_2$ was calculated with Equation 9 with the weights $W_i$ and $R_i$ values defined. $I{R}_3$ was calculated with Equation 9 as well, but with a constant value for the weights $W_i=0.25$ (equal weights).

Table 4
Partial and final resilience indexes.

No.	Section	Scenario	R1	R2	R3	R4	IR2	IR3
1	PS1 - PS2	Qop with Booster	0.86	-0.89	0.96	0.58	0.54	0.38
2	PS1 - PS2	Qop with Booster - Shutdown one pump set	0.86	-0.20	0.96	0.58	0.62	0.55
3	PS1 - PS2	Qop with Booster - Shutdown two pump set	0.86	-0.66	0.96	0.58	0.56	0.44
4	PS1 - PS2	Qop with Booster - Shutdown tree pump set	0.86	-0.66	0.96	0.58	0.56	0.44
5	PS1 - PS2	Qop with Booster - Shutdown Booster	0.83	-0.20	0.96	0.58	0.61	0.54
6	PS1 - PS2	Qop without OWT 1	0.65	-0.96	0.92	-0.41	0.03	0.05
7	PS1 - PS2	Qop without OWT 2	0.79	-0.96	0.95	0.29	0.38	0.27
8	PS1 - PS2	Qop without OWT 3	0.79	-0.96	0.96	0.40	0.42	0.29
9	PS1 - PS2	Qop without Valve 2	0.82	-0.96	0.96	0.54	0.49	0.34
10	PS1 - PS2	Qop without protection devices	0.36	-0.96	0.92	-0.86	-0.27	-0.13
11	PS1 - PS2	Qop - shutdown one pump set	0.85	0.38	0.96	0.58	0.69	0.69
12	PS1 - PS2	Qop - shutdown two pump set	0.85	-0.66	0.96	0.58	0.56	0.43
13	PS1 - PS2	Qop - shutdown tree pump set	0.83	-0.89	0.96	0.58	0.52	0.37
14	PS1 - PS2	Qop - Starting tree pump set	0.80	0.20	0.96	0.41	0.58	0.59
15	PS1 - PS2	Qop - Damaged shaft	0.81	-0.96	0.96	0.49	0.47	0.33
16	PS1 - PS2	Qop - without valves	0.82	-0.89	0.96	0.55	0.51	0.36
17	PS1 - PS2	Q = 1,5 Qop	0.41	0.96	0.87	-0.54	0.12	0.43
18	PS1 - PS2	Q = 1,5 Qop with booster	0.59	-0.96	0.83	0.14	0.23	0.15
19	PS2 - WTP	Qop with booster	0.80	-0.96	0.96	0.58	0.50	0.34
20	PS2 - WTP	Qop with booster - shutdown one pump set	0.80	-0.20	0.96	0.58	0.60	0.54
21	PS2 - WTP	Qop with booster - shutdown two pump set	0.80	-0.20	0.96	0.58	0.60	0.54
22	PS2 - WTP	Qop with booster - shutdown tree pump set	0.80	-0.96	0.96	0.58	0.50	0.34
23	PS2 - WTP	Qop with booster - shutdown booster	0.79	0.20	0.96	0.51	0.61	0.61
24	PS2 - WTP	Qop without valves	0.79	-0.96	0.96	0.16	0.32	0.24
25	PS2 - WTP	Qop without OWT 4	0.79	-0.96	0.96	0.56	0.49	0.34
26	PS2 - WTP	Qop without OWT 5	0.79	-0.96	0.96	0.51	0.47	0.32
27	PS2 - WTP	Qop without OWT 6	0.79	-0.96	0.96	0.52	0.47	0.33
28	PS2 - WTP	Qop without OWT 7	0.79	-0.96	0.96	0.51	0.47	0.32
29	PS2 - WTP	Qop without devices	0.24	-0.96	0.95	-0.27	-0.08	-0.01
30	PS2 - WTP	Qop without check valve	0.77	-0.76	0.96	0.52	0.49	0.37
31	PS2 - WTP	Qop - shutdown one pump set	0.79	0.00	0.96	0.58	0.61	0.58
32	PS2 - WTP	Qop - shutdown two pump set	0.79	0.00	0.96	0.58	0.61	0.58
33	PS2 - WTP	Qop - shutdown tree pump set	0.79	-0.96	0.96	0.58	0.50	0.34
34	PS2 - WTP	Qop - Starting tree pump set	0.75	0.00	0.96	0.38	0.52	0.52
35	PS2 - WTP	Qop - Damaged shaft	0.77	-0.96	0.96	0.52	0.47	0.32
36	PS2 - WTP	Q = 1,5 Qop	0.74	-0.96	0.96	0.35	0.38	0.27
37	PS2 - WTP	Q = 1,5 Qop with booster	0.74	-0.96	0.96	0.43	0.42	0.29

The value of $I{R}_1$, calculated as the minimum value among $R_i$, is too conservative and makes the analysis difficult, as also mentioned by Wang et al. (2014), so $I{R}_1$ was not included on the final analysis. The values of $I{R}_2$ and $I{R}_3$ are shown in Figures 4 and 5 decrescent order from the highest to lowest value of the resilience indexes. Remembering that positive values near one denotes elevated resilience conditions.

Figure 5
Final Resilience Index, section PS1-PS2.

When the booster is maintained operating the resilience indexes are higher, confirming the importance of using this equipment. The use of the booster creates a discontinuity in the piezometric line which helps to reduce the higher value of the overpressure wave transients. In addition, the initial head on the pumps is lower since the delivery point is the booster rather than the reservoir at the end of the pipeline.

From Figures 5 and 6, it is noticeable that the values are more homogeneous for $I{R}_2$ whilst $I{R}_3$ has a superior variation. However, both indexes present the same tendencies (lower values in the same scenarios). The lowest resilience indexes correspond to the scenarios where all protection devices fail or the flow rate increases by 50%, which corresponds to the physical reality and the theory, since when there is no protection, the pressures exceed the system's capacity and failure is highly likely. An increase in flow also leads to an increase in velocity, which increases the peak pressure wave of the transient.

Figure 6
Final Resilience Index, section PS2-WTP.

OWT’s (one-way tanks) varies in importance at each section. In the first section it is more critical to remove OWT1 than any of the others since the pressure is higher at the beginning of the pipeline. In the second section the resilience index for the OWT’s is more homogeneous, as the variation in heights is smaller.

CONCLUSIONS

Often the analysis of hydraulic transients is neglected in the design of pipelines, and only evaluated for longer water mains with larger diameter and steep locations. The lack of analysis in medium and small projects leads to ruptures and economic losses for companies and users.

To complement the methodology of Wang et al. (2014), the calculation of the weights using the hierarchical analytical process (AHP) was implemented. This does not require a large amount of data and it considers the experience of the decision maker. If the calculations are not clear to the user, or information is missing, it is possible to assume an equal value to the weights which maintains a similar trend to the AHP.

The indexes developed in this work can be applied to the identification of critical scenarios, identification of piping stretches at higher risk, prioritization of transient damping devices, prioritization of preventive maintenance actions, among other applications in research, projects, and pipeline operation.

For instance, the case study presented here, trunk main of Rio Canoas in Franca/SP, had an evaluation of the transients hydraulic in the design stage, but currently operates under different conditions as several modifications were undertaken. Therefore, resilience indexes were applied to estimate the susceptibility of the pipeline to extreme conditions. The resilience indexes were calculated using parameters related to infrastructure capacity, fluid characteristics, operational effects, and transient flow conditions. Given the three ways evaluated to calculate the final resilience index (IR) it is recommended to apply the methodologies that consider all parameters even if equal weights are assigned. The safety coefficient for parameter undermining was not implemented in the IR calculations to avoid the loss of sensitivity when comparing scenarios, since the index tends to show a more homogeneous result.

ACKNOWLEDGEMENTS

This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brasil (CAPES) – Finance Code 001.

REFERENCES

• Babayan, A. V., Savic, D. A., Walters, G. A., & Kapelan, Z. S. (2007). Robust least-cost design of water distribution networks using redundancy and integration-based methodologies. Journal of Water Resources Planning and Management, 133(1), 67-77. http://doi.org/10.1061/(ASCE)0733-9496(2007)133:1(67)
  » http://doi.org/10.1061/(ASCE)0733-9496(2007)133:1(67)
• Boulos, P. F., Karney, B. W., Wood, D. J., & Lingireddy, S. (2005). Hydraulic transient guidelines for protecting water distribution systems. Journal - American Water Works Association, 97(5), 111-124. http://doi.org/10.1002/j.1551-8833.2005.tb10892.x
  » http://doi.org/10.1002/j.1551-8833.2005.tb10892.x
• Cemil, Tubos e Conexões Ltda. (2023). Catálogo de Produtos da Cemil Tubos e Conexões São Paulo. Retrieved in 2023, December 13, from https://www.cemiltubos.com.br/pdf/catalogo-cemil.pdf
  » https://www.cemiltubos.com.br/pdf/catalogo-cemil.pdf
• Crabtree, A., & Oliphant, K. (2012). Resistance of PE4710 Piping to Pressure Surge Events in Force Main Applications. In Plastic Pipes Conference Association 2012 Barcelona. Retrieved in 2023, December 13, from https://www.pe100plus.com/PPCA/Resistance-of-PE4710-Piping-Materials-to-Pressure-Surge-Events-in-Force-Main-Applications-p475.html
  » https://www.pe100plus.com/PPCA/Resistance-of-PE4710-Piping-Materials-to-Pressure-Surge-Events-in-Force-Main-Applications-p475.html
• D’Ercole, M., Righetti, M., Raspati, G. S., Bertola, P., & Maria Ugarelli, R. (2018). Rehabilitation planning of water distribution network through a reliability: based risk assessment. Water (Basel), 10(3), 277. http://doi.org/10.3390/w10030277
  » http://doi.org/10.3390/w10030277
• Feng, Y. X., Zhang, H., Rad, S., & Yu, X. Z. (2021). Visual analytic hierarchical process for in situ identification of leakage risk in urban water distribution network. Sustainable Cities and Society, 75, 103297. http://doi.org/10.1016/j.scs.2021.103297
  » http://doi.org/10.1016/j.scs.2021.103297
• Guo, D., Shan, M., & Owusu, E. K. (2021). Resilience assessment frameworks of critical infrastructures: state-of-the-art review. Buildings,11(10), 464. https://doi.org/10.3390/buildings11100464.
  » https://doi.org/10.3390/buildings11100464.
• Hussain, A., Mustafa, M., Warsi, S. A., & Kumar, S. (2021). Water hammer analysis for pipeline network using HAMMER V8i. In R. Jha, V.P. Singh, V. Singh, L.B. Roy and R. Thendiyath (Eds.), Water Resources Management and Reservoir Operation: Hydraulics, Water Resources and Coastal Engineering (Water Science and Technology Library, pp. 117-127). USA: Springer.
• Jayaram, N., & Srinivasan, K. (2008). Performance‐based optimal design and rehabilitation of water distribution networks using life cycle costing. Water Resources Research, 44(1), 2006WR005316. http://doi.org/10.1029/2006WR005316
  » http://doi.org/10.1029/2006WR005316
• Kaaviya, R., & Devadas, V. (2021). Water resilience mapping of Chennai, India using analytical hierarchy process. Ecological Processes, 10, 71. http://doi.org/10.1186/s13717-021-00341-1
  » http://doi.org/10.1186/s13717-021-00341-1
• Kapelan, Z. S., Savic, D. A., & Walters, G. A. (2005). Multiobjective design of water distribution systems under uncertainty. Water Resources Research, 41(11), 2004WR003787. http://doi.org/10.1029/2004WR003787
  » http://doi.org/10.1029/2004WR003787
• Klein, R. J., Nicholls, R. J., & Thomalla, F. (2003). Resilience to natural hazards: how useful is this concept?Global Environmental Change Part B: Environmental Hazards,5(1), 35-45.
• Komolafe, A. A., Olorunfemi, I. E., Akinluyi, F. O., Adeyemi, M. A., & Ajayi, J. A. (2021). Enhanced flood hazard modelling using hydraulic, analytical hierarchical process and height above nearest drainage models in Ogunpa river basin, Ibadan, Southwestern Nigeria.Modeling Earth Systems and Environment,7, 967-981. https://doi.org/10.1007/s40808-020-01037-9
  » https://doi.org/10.1007/s40808-020-01037-9
• Li, S., Wang, R., Wu, W., Sun, J., & Jing, Y. (2015). Non-hydraulic factors analysis of pipe burst in water distribution systems. Procedia Engineering, 119, 53-62. http://doi.org/10.1016/j.proeng.2015.08.853
  » http://doi.org/10.1016/j.proeng.2015.08.853
• Liao, R., Jin, Z., Chen, M., & Li, S. (2020). An integrated approach for enhancing the overall performance of constructed wetlands in urban areas. Water Research, 187, 116443. http://doi.org/10.1016/j.watres.2020.116443.
• Rajkumar, H., Naik, P. K., & Rishi, M. S. (2022). A comprehensive water quality index based on analytical hierarchy process. Ecological Indicators, 145, 109582. http://doi.org/10.1016/j.ecolind.2022.109582
  » http://doi.org/10.1016/j.ecolind.2022.109582
• Saaty, T. L. (1980). The analytic hierarchy process: planning, priority setting, resource allocation New York: Mcgraw-Hill.
• Saint-Gobain Canalização Ltda. (2021). Catálogo Saint-Gobain Canalização Rio de Janeiro. Retrieved in 2023, December 18, from https://sic.cagepa.pb.gov.br/_lib/file/doc/licitacao/CAT%C3%81LOGO%20GERAL%20SAINT%20GOBAIN.pdf
  » https://sic.cagepa.pb.gov.br/_lib/file/doc/licitacao/CAT%C3%81LOGO%20GERAL%20SAINT%20GOBAIN.pdf
• Sutadian, A. D., Muttil, N., Yilmaz, A. G., & Perera, B. J. C. (2017). Using the Analytic Hierarchy Process to identify parameter weights for developing a water quality index. Ecological Indicators, 75, 220-233. http://doi.org/10.1016/j.ecolind.2016.12.043
  » http://doi.org/10.1016/j.ecolind.2016.12.043
• Tawfik, A. (2023). Air vessel sizing approach for pipeline protection using artificial neural networks. Journal of Engineering and Applied Sciences (Asian Research Publishing Network), 70(1), 1-19. http://dx.doi.org/10.1186/s44147-023-00206-8
  » http://dx.doi.org/10.1186/s44147-023-00206-8
• Todini, E. (2000). Looped water distribution networks design using a resilience index based heuristic approach. Urban Water, 2(2), 115-122. http://doi.org/10.1016/S1462-0758(00)00049-2
  » http://doi.org/10.1016/S1462-0758(00)00049-2
• Tornyeviadzi, H. M., Neba, F. A., Mohammed, H., & Seidu, R. (2021). Nodal vulnerability assessment of water distribution networks: an integrated Fuzzy AHP-TOPSIS approach. International Journal of Critical Infrastructure Protection, 34, 100434. http://doi.org/10.1016/j.ijcip.2021.100434
  » http://doi.org/10.1016/j.ijcip.2021.100434
• Tullis, J. P. (1989).Hydraulics of pipelines: pumps, valves, cavitation, transients Hoboken: John Wiley & Sons. http://doi.org/10.1002/9780470172803
  » http://doi.org/10.1002/9780470172803
• Ulusoy, A. J., Mahmoud, H. A., Pecci, F., Keedwell, E. C., & Stoianov, I. (2022). Bi-objective design-for-control for improving the pressure management and resilience of water distribution networks. Water Research, 222, 118914. http://doi.org/10.1016/j.watres.2022.118914.
• Walski, T. M., Chase, D. V., Savic, D. A., Grayman, W., Beckwith, S., & Koelle, E. (2003). Advanced water distribution modeling and management Civil and Environmental Engineering and Engineering Mechanics Faculty Publications. Paper 18. Retrieved in 2023, December 18, from http://ecommons.udayton.edu/cee_fac_pub/18
  » http://ecommons.udayton.edu/cee_fac_pub/18
• Wan, W., Chen, X., Zhang, B., & Lian, J. (2021). Transient simulation and diagnosis of partial blockage in long-distance water supply pipeline systems. Journal of Pipeline Systems Engineering and Practice, 12(3), 04021016. http://doi.org/10.1061/(ASCE)PS.1949-1204.0000562
  » http://doi.org/10.1061/(ASCE)PS.1949-1204.0000562
• Wang, R., Wang, Z., Wang, X., Yang, H., & Sun, J. (2014). Pipe burst risk state assessment and classification based on water hammer analysis for water supply networks. Journal of Water Resources Planning and Management, 140(6), 04014005. http://doi.org/10.1061/(ASCE)WR.1943-5452.0000404
  » http://doi.org/10.1061/(ASCE)WR.1943-5452.0000404
• Wang, Z., He, X., Zhang, C., Xu, J., & Wang, Y. (2020). Evaluation of geological and ecological bearing capacity and spatial pattern along du-wen road based on the analytic hierarchy process (AHP) and the technique for order of preference by similarity to an ideal solution (TOPSIS) method. ISPRS International Journal of Geo-Information, 9(4), 237. http://doi.org/10.3390/ijgi9040237
  » http://doi.org/10.3390/ijgi9040237
• Wylie, E. B., Streeter, V. L., & Suo, L. (1993).Fluid transients in systems(Vol. 1, pp. 464). Englewood Cliffs: Prentice Hall. http://doi.org/10.1017/S0022112094210716
  » http://doi.org/10.1017/S0022112094210716
• Xu, S., Zhu, X., Tan, Y., & Chen, C. (2023). Water hammer protection measures and calculation analysis of reservoir water pipelines. Journal of Physics: Conference Series, 2441(1), 012049. http://doi.org/10.1088/1742-6596/2441/1/012049
  » http://doi.org/10.1088/1742-6596/2441/1/012049
• Xue, Y., Yue, L., Ding, R., Zhu, S., Liu, C., & Li, Y. (2023). Influencing mechanisms of gas bubbles on propagation characteristics of leakage acoustic waves in gas-liquid two-phase flow. Ocean Engineering, 273, 114027. http://doi.org/10.1016/j.oceaneng.2023.114027
  » http://doi.org/10.1016/j.oceaneng.2023.114027
• Yu, X., Wu, Y., Zhou, X., & Liu, S. (2023). Resilience evaluation for water distribution system based on partial nodes’ hydraulic information. Water Research, 241, 120148. http://doi.org/10.1016/j.watres.2023.120148
  » http://doi.org/10.1016/j.watres.2023.120148
• Zhang, B., & Wan, W. (2022). A transient-features-based diagnostic method of multi incipient cracks in pipeline systems. International Journal of Pressure Vessels and Piping, 199, 104701. http://doi.org/10.1016/j.ijpvp.2022.104701
  » http://doi.org/10.1016/j.ijpvp.2022.104701

Edited by

• Editor-in-Chief:
  Adilson Pinheiro

• Associated Editor:
  Fábio Veríssimo Gonçalves

Publication Dates

• Publication in this collection
  09 Dec 2024
• Date of issue
  2024

History

• Received
  09 Jan 2024
• Reviewed
  08 Aug 2024
• Accepted
  17 Sept 2024