Application of the first canonical variable in the evaluation of animal production trials

Aplicação da primeira variável canônica na avaliação de experimentos de desempenho produtivo com animais

RUMINANTES

Application of the first canonical variable in the evaluation of animal production trials

Aplicação da primeira variável canônica na avaliação de experimentos de desempenho produtivo com animais

Edenio Detmann^I; Paulo Roberto Cecon^II; Marcelo de Oliveira Andreotti^III,*; Flávio Dutra de Resende^IV; Daniel de Paula Sousa^V; Niraldo José Ponciano^VI; José Maurício de Souza Campos^VII; Paulo Marcelo de Souza^VI; Andrea Vittori^VIII

^IZootecnista, D.Sc., Professor Adjunto, Departamento de Zootecnia, Universidade Federal de Viçosa, Viçosa-MG, Brazil, 36571-000, Bolsista do CNPq ([e-mail])

^IIEngº. Agrônomo, D.Sc., Professor Adjunto, Departamento de Informática, UFV, Bolsista do CNPq ([e-mail])

^IIIZootecnista, D.Sc., Professor Adjunto, Departamento de Produção Animal, Universidade Federal de Mato Grosso do Sul, Campo Grande-MS

^IVZootecnista, D.Sc., Pesquisador, Instituto de Zootecnia do Estado de São Paulo, Colina-SP, Brazil

^VZootecnista, M.Sc., Estudante de Doutorado, Departamento de Zootecnia, ESALQ-USP

^VIEngº. Agrônomo, D.Sc., Professor Associado, LEAG-UENF, Campos dos Goytacazes-RJ

^VIIEngº. Agrônomo, D.Sc., Professor Adjunto, DZO-UFV

^VIIIEngª. Agrônoma, D.Sc

ABSTRACT

The objective of this work was to evaluate the inter treatment discrimination according to feed conversion efficiency in several animal performance experiments. The variables investigated were: feed conversion ratio (FCR = intake: production ratio), feed efficiency index (FEI = production: intake ratio) and bio-nutritional index (BNI). The BNI was constructed from the first canonical variable obtained based on the multivariate analysis of variance of the intake and animal production (weight gain or milk production) variables. The results indicated that FCR and FEI reciprocated each other at experimental plot level but did not reciprocate at animal group or treatment level. This fact implicates distortions on the descriptive levels of probability of type I error for hypotheses tests and compromises the statistical and animal production inferences. On the other hand, the BNI index guarantees the maximum discrimination among experimental groups and allows to identify significant differences, which were not observe with FCR or FEI indexes. This fact can be associated to the incorporation of animal production intensity characteristics using BNI.

Key Words: bio-nutritional index, cattle, feed conversion ratio, feed efficiency index, multivariate statistical analysis, poultry

RESUMO

Objetivou-se avaliar os aspectos de discriminação da eficiência de transformação alimento:produto entre tratamentos em um grupo de experimentos de desempenho produtivo animal utilizando-se os índices conversão alimentar (CA = consumo/produção), eficiência alimentar (EA = produção/consumo) e índice bionutricional (IBN). O IBN foi constituído a partir da primeira variável canônica obtida pela análise de variância multivariada do consumo e da produção animal (ganho de peso ou produção de leite). Os resultados evidenciam que CA e EA, embora recíprocos em nível de unidade experimental, não apresentam a mesma tendência em nível de grupo experimental, o que implica distorções sobre os níveis descritivos de probabilidade para o erro tipo I associados aos testes de hipóteses e compromete as inferências estatísticas e produtivas. Por outro lado, o IBN garantiu máxima discriminação entre grupos experimentais, permitindo a identificação de diferenças significativas, não perceptíveis por CA e EA, o que parece ser conseqüência da incorporação de características de intensidade de produção, associada à aplicação do IBN.

Palavras-chave: análise multivariada, aves, bovinos, conversão alimentar, eficiência alimentar, índice bionutricional

Introduction

Research in animal feeding and nutrition is a dynamic process that search continuously for alternative diets that fullfill economical and/or nutritional requirements (Crampton, 1934; Guidoni, 1994).

Although the list of response-variables in animal nutrition and performance studies is large and particular to each animal species, voluntary feed intake and production variables (e.g. weight gain, and milk, egg, and wool yields, etc) are the most studied topics in the majority of animal research.

However, inferences in animal nutrition usually require a index that indicates the efficiency of feed conversion to animal product. Therefore, these indexes can be generated by dividing feed intake per animal product unit (intake:production ratio), called feed conversion ratio (FCR) or by dividing animal production per feed intake unit (production: intake ratio), called feed efficiency index (FEI).

The FCR and FEI are response-variables largely used in researches associated with both animal nutrition and production. However, some important aspects in which statistics and animal variables interact are commonly disregard and as result may compromise inferences from FCR and FEI.

Voluntary feed intake and animal product are mutually correlated continuous random variables that follow the normal probability distribution (Guidoni, 1994). If this is true, the formation of a new variable from intake:production ratio, consisting of a non-linear combination, will lead to distortions on the statistical procedures and inferences in situations where strict conditions are not achieved. Among these conditions are a positive linear relationship with a null intercept and heterogeneous variances that must be proportional to the magnitudes of both original variables (Weill Jr., 1962). Furthermore, the ratio between two variables with normal distribution may not show normal distribution. In this case, it approaches the non-parametric distribution of Cauchy. In this context, the majority of statistical methods employed in the discrimination among experimental groups are applicable only to variables that are normally distributed and with homogeneous intra-group variances. Thus, the comparative evaluation through ratios may result in sophisms about statistical inferences.

Generation of a variable using either the intake: production or production: intake ratios implies that all ingested feed is converted to animal product. However, this assumption does not take into account that a significant portion of feed is utilized for maintenance requirements. Thus, variations in the portion of feed used for maintenance of basal metabolism will imply in biases that may not be easily detected if animal production inferences are made from FCR or FEI.

Furthermore, the use of both FCR and FEI seems to have limited application in conditions where extremely low intakes or absent or negative productions are observed. In the case of negative production, the situation is worse because negative weight gains imply in incoherent biological values for FCR and FEI. In addition, lack of production generates a mathematical indetermination about the FCR estimates.

On the other hand, different from FCR and FEI, the linear combination of two normally distributed variables produces a new variable with normal distribution (Fonseca & Martins, 1982). Thus, any linear combination between animal production and voluntary feed intake will result in a new one-dimensional and normally distributed random variable that will encompass their characteristics. In this way, the linear combination between these variables, which is made under certain statistical principles has been indicated as an analytical alternative to the ratio indexes in comparative evaluation of nutritional efficiency. This variable is called first discriminant canonical variable or just first canonical variable (FCV) (Guidoni, 1994).

The FCV is composed of an optimized linear combination of a multiple measures group that is better than any other linear combination allowing the discrimination among classes or groups (Fisher, 1938). This maximizes the variations among classes or groups and minimizes the intra-group variation (residual variance) (Fisher, 1936).

The FCV composed of voluntary feed intake and animal production was named the bio-nutritional efficiency by Euclides Filho et al. (2001) and then bio-nutritional index (BNI) in the present work. In spite of its statistical advantages over the FCR and FEI, application of FCV has been restricted to few studies with poultry (Guidoni, 1994) and beef cattle (Euclides Filho et al., 2001, 2002; Gesualdi Jr. et al., 2003) in Brazil. Thus, few comparative data among these different indexes are present in the literature, which restrict the knowledge and the methodological and discursive divulgation about using BNI in animal trials.

Therefore, the objective of this work was to compare the efficiency of feed conversion to animal products in several production trials using FCR, FEI and BNI. It was of particular interest to discuss some methodological and inference aspects associated to using the BNI.

Material and Methods

Data used in the statistical analyses were obtained from two different experiments with poultry (Andreotti, 2002) and from three trials with cattle (Resende et al., 2000; Vittori et al., 2001; Sousa et al., 2002), that reported dry matter intake and weight gain or milk production. It is important to emphasize that the statistical analyses done in the present work preserved the majority of the original analyses. Refer to the original references for more details about the experimental procedures and the biological interpretation of the results.

Experimental descriptions summary

Experiment 1 - Andreotti (2002)

The experiment was conducted with 1200 twenty-one-days-old Cobb breed male chickens with initial average weight of 868 g. Animals were housed in 30 boxes equipped with semi-automatic tubular feedbins and pendular water source and had ad libitum access to feed.

Diets were formulated to be isonitrogenous and isoenergetic, all containing corn grains and soybean meal plus one of six lipid sources: T1 - pork oil; T2 - canola oil; T3 - chicken oil; T4 - sunflower oil; T5 - corn oil; or T6 - soybean oil. Both feed intake and weight gain were measured from day 21 to 42.

The experiment was analyzed as a completely randomized design with six treatments and five replications each (box with 30 birds).

Experiment 2 - Andreotti (2002)

The experiment was carried out with 840 twenty-one-days-old Cobb breed male chickens, with average initial weight of 870 g. Animals were housed in 24 boxes equipped with semi-automatic tubular feedbins and pendular water source and had ad libitum access to feed. Diets were formulated to be isonitrogenous and isoenergetic and had different concentrations of soybean oil on as-fed basis: T1 - 0%, T2 - 3.3%, T3 - 6.6%, and T4 - 9.9%.

Both feed intake and weight gains were measured from day 21 to 42. The experiment was analyzed as a completely randomized design with four treatments and six replications each (box with 35 birds).

Experiment 3 - Resende et al. (2000)

The experiment was conducted using 56 young bulls from the following genetic groups: Nellore, Guzera, Gyr and Caracu. With the exception of one out of two Nellore groups, all other genetic groups were submitted to selection based on the body weight at 378 days of age.

Animals were fed isonitrogenous diets containing corn silage and concentrate that were fed in two forage: concentrate ratios on a dry matter basis (60:40 or 40:60). Animals were slaughtered when they achieved 4 mm of fat thickness in the 12^th/13^th rib height that was estimated by ultra-sonography.

The experiment was carried out as a completely randomized design with a 2 x 5 factorial arrangement (two forage:concentrate ratios and five genetic groups). Bulls were stall housed either individually or in pairs. When in pairs, both feed intake and average weight gain were collectively computed. Thus, stall was the experimental unit. Replications for the different treatments ranged from two to four leading to a total of 30 experimental plots.

Experiment 4 - Vittori et al. (2001)

The trial was done using 86 bulls or steers from the following genetic groups: Nellore, Guzera, Gyr, and Caracu. With the exception of one out of two Nellore groups, all other genetic groups were submitted to selection based on the body weight at 378 days of age. Animals had free acess to a diet containing a corn silage to concentrate of 60:40. Animals were slaughtered when they achieved 4 mm of fat thickness in the 12^th/13^th rib height that was estimated by ultra-sonography.

A completely randomized design with a 5 x 2 factorial arrangement (five genetic groups and bulls or steers) was used in Vittori el al. (2001) trial. Animals were stall housed either individually or in pairs. When in pairs, both feed intake and average weight gain were collectively computed. Thus, stall was the experimental unit. Replications for the different treatments varied from three to five leading to a total of 41 experimental plots.

Experiment 5 - Sousa et al. (2002)

Twelve Holstein dairy cows were blocked by days in milk and randomly assigned to three 4 x 4 Latin squares with 21 days period (14 days for diet adaptation and 7 days for sample collection). Cows were individually fed twice a day after milkings. Diets were formulated to be isonitrogenous containing (dry matter basis) a forage to concentrate ratio of 60:40. The following treatments were used: corn silage (T1), all sugar cane (T2) and replacement of sugar cane with 7% (T3) and 14% (T4) by whole cotton seed. Urea and ammonium sulphate (9:1) were mixed with sugar cane in a proportion of 100:1 (as-fed basis).

The multivariate analyzis of variance (MANOVA) (Johnson & Wichern 1998) was used to analyze all five trials. The experimental design of each trial was mantained except in experiments 3 and 4 where the factorial arrangment was removed from the analysis. The following models were used:

where: = vector of response variables (weight gain detmann et al. and feed intake); = vector of general constants; _i = vector of i^th treatment effects; _j = vector of j^th Latin square effects; = vector of effects of the k^th period nested to the j^th Latin square; _(j)l = vector of effects of the l^th animal nested to the j^th Latin square; q_ij = vector of interaction effects between the i^th treatment and the j^th Latin square; and _(i)j or _ijkl = vector of random errors which were presupposed of the bivariated normal distribution with vector of averages and variances and co-variances matrix S.

From the information generated by the MANOVA, the eingenvalues associated with the "treatments" sums of squares matrix were obtained by the characteristic equation (Harris 1975; Cruz & Regazzi, 2001):

where: E^-1 = common inverse matrix of the residual sums of squares; H = matrix for the "treatments" sums of squares; l = canonical eingenvalue; and I = identity matrix.

From the higher canonical eingenvalue obtained through the characteristic equation (3), the correspondent non-normalized eigenvector was estimated through the solution of the following equation system (Searle, 1966):

where: l₁ = higher canonical eigenvalue; 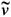= non-normalized eigenvector associated to the higher canonical eingenvalue; a and b = canonical coefficients; and E^-1, H e I = as defined before.

Afterwards, the normalization of the eingenvector obtained in (4) was obtained according to the restriction:

where:

_n = normalized eingenvector associated to the higher canonical eigenvalue; a' and b' = canonical coefficients of the normalized eingenvector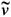 ; and E = matrix of residual sum of squares.

From the normalized canonical eingenvector coefficients defined in (5) a new variable named FCV or BNI was produced:

where: DMI = dry matter intake; PROD = animal production (weight gain or milk production); and a' and b' = as defined before.

The BNI, FCR and FEI were all submitted to a univariate analysis of variance according to the models described in (1) and (2) taking into account the factorial arrangement of experiments 3 and 4.

Results and Discussion

According to the assumptions of the performance experiments, the equivalence between the ratio indexes of the feed transformation efficiency to animal product is verified through the relation:

Although this relation can be easily verified at experimental unit level such equivalence cannot be maintained at the group or treatment level evaluation.

Thus, the computation of the individual observations for FCR and FEI can provide different productive efficiency estimates. This fact can be proven by verifying the divergences between the arithmetic mean of FEI observations and the reciprocal of arithmetic mean of FCR (Table 1). These divergences seem to be more evident in the experiments done with cattle (possibly caused by the lower experimental precision of cattle trials compared to poultry trials) suggesting that the ratio indexes are not able to evaluate production trials similarly.

The evaluation based on the reciprocal equivalence between FCR and FEI (Equation 7) does not consider the fact that the point estimator for FCR is the arithmetic mean but it will not be for its reciprocate, which is correctly estimated by the harmonic mean (Guidoni, 1994). This relation is supported by the exact convergence between the FEI estimates obtained through the reciprocate of FCR arithmetic mean and by the harmonic mean of the observations in all experimental results presented in Table 1.

Therefore, according to Guidoni (1994) if the harmonic mean is smaller than the arithmetic mean the use of FCR will underestimate whereas the use of FEI will overestimate animal performance. Such behavior can compromise the productive inferences obtained from these indexes.

The coefficients used in the BNI for each experiment and the relative importance of the higher eingenvalues (RIE) are shown in Table 2. The RIE indicates the fraction of total discrimination power among experimental treatments/groups, which was kept after reduction of Euclidian space of comparison from two (feed intake and animal production) to one dimension only (BNI).

Thus, the high discrimination power associated with the BNI in all experiments can be confirmed (Table 2) generating an initial prerogative over the BNI based on the small information lost in the transition to the univariated context, that is associated with an elevated analytical gain.

To better understand coefficients presented in Table 2, a short analytical approach must be done.

The majority of animal performance experiments has a complex experimental structure with factorial arrangements (e.g. Experiments 3 and 4) or by using decomposition of the treatments sum of squares in orthogonal components (e.g. Experiment 5). Under these circumstances and in an analytical point of view, more than one sums of squares matrix associated with the known sources of variation with experimental interest (matrix H - Equation 3) can be evaluated (e.g. principal factors, interactions, orthogonal contrasts, etc). As a consequence, each matrix will allow the building of a FCV that will be applicable to the maximum discrimination among groups according to the evaluated source of variation (Harris, 1975).

Therefore, an experimental-analytical problem is to identify the source of variation that will provide the basic matrix to obtain the BNI. The use of several BNI associated with each source of variation originated from the decomposition of the treatments sums of square does not constitute a rational solution and have no contribution to the operational gain obtained with the reduction of the Euclidian space of discrimination from two to one dimension.

On the other hand, an alternative analytical approach is the use of the matrix associated with the "treatments" source of variation to estimate BNI (Harris, 1975). In this case, only the basic structure of the statistical design (e.g. completely randomized design, Latin square design, randomized complete block design, etc) is used to estimate BNI rather than the complex experimental structures (e.g. factorial arrangement and orthogonal contrasts). The statistical arrangement would be used only after obtaining BNI estimates in univariate analysis. This was adopted to interpret the experiments described in this study. In this context, the utilization of the matrix of "treatments" sums of squares as the H matrix (Equation 3) allows higher discrimination among experimental groups according to the design adopted to the experiment. Thus, global tendencies about the other sources of variation would consequently be emphasized by the estimated discriminating function if their effects were significant.

These arguments support a pattern to the general analytical proposal to obtain BNI. However, some authors have estimated the BNI based on the interaction sums of squares matrix in experiments with factorial arrangements (Euclides Filho et al., 2001, 2002). It is obvious that such option does not compose an analytical sophism but emphasizes that a standard analytical procedure becomes necessary to guarantee better precision in the comparison of inferences obtained in different trials.

The statistical results for the Experiments 1, 2, 3, 4 and 5 are shown in Tables 3, 4, 5, 6, and ⁷, respectively. Overall, independent of the experiment analyzed, it were observed divergences among the descriptive probability levels for the type I error in the different sources of variation evaluated using the FCR and FEI (Tables 3 to 7). Such behavior associates one more incoherent interpretation of the pre-supposed similarity among these indexes.

Guidoni (1994) affirmed that this fact constitutes enough argument to establish that the statistical hypotheses tested by FCR and FEI are different and can interfere in the inference making when the descriptive levels of probability put themselves near the established critical limit (a).

Although the structure of the hypotheses for FCR and FEI is done similarly in an individual context, data restructuring caused by the reciprocate transformation can imply in an alteration of the residual structure, deviating the probability levels, causing the hypothesis tests to be statistically not equivalent. These aspects add to the list of compromising inferences to be obtained based on ratio indexes.

On the other hand, the results obtained in Experiment 1 (Table 3) permit to initially illustrate two important aspects associated with the BNI.

First, the high retention of discrimination aspects among groups associated with the BNI allowed the verification of differences among treatments that was not observed when using FCR and FEI (Table 3). A similar behavior was also observed for the results of Experiments 4 and 5 (Tables 6 and ⁷, respectively).

Then, it becomes important to bring into prominence that the discrimination by using BNI does not give an inter-groups difference, but only equalizes the linear combination among the original variables so that one can obtain the maximum value of calculated F statistic (Harris, 1975). This optimizes the discrimination based exclusively on the original information and makes Application of the First Canonical Variable in the Evaluation of Animal Production Trials clear the real divergences among the groups.

Second, the information obtained from the results in Experiment 1 allows to point out another apparent animal production advantage associated with BNI. Considering the treatments 2 and 5, opposite extremes of multiple comparisons profile for BNI (Table 3), it can be observed that, although it shows distinctions in relation to this variable, they have a numerical similarity with FCR and FEI. A more detailed analysis of the information on Table 1 reveals that although the feed is converted in a similar ratio, the animals on treatment 5 showed greater intake and weight gain characterizing greater production intensity.

In a hypothetical example, two animal groups with intakes of X and 2X, and weight gain of Y and 2Y, respectively, would have same FCR and FEI but different BNI. This discriminating aspect in relation to the production intensity associated with BNI has direct consequences to the interpretation from an animal production point of view. Even using feed similarly, animals with greater production intensity will be more productive per units of time and physical space. In the long term, differentiation in other productive efficiency aspects through a possible dilution of maintenance requirements in a systemic may be verified. Therefore, the discrimination through BNI is wider than FCR and FEI because it incorporates animal development intensity elements not perceptible by using these ratio indexes.

In Experiment 2 there were similarities in the inference based on the hypothesis associated to the "treatments" effect and their orthogonal components from different indexes with a convergence to the second order effect of soybean oil levels in the diets (Table 4). However, the evaluation of the data through least square regressions indicated distinct critical points for each index. These were over the 7.92%, 8.03%, and 9.41% of soybean oil concentrations for the FCR, FEI and BNI, respectively.

Once more the different critical points observed between FCR and FEI, emphasize the fact that these indexes, although considered equivalent may produce divergent inferences (Guidoni, 1994). On the other hand, the oil concentration of the more elevated critical point for BNI can possibly be supported by the incorporation of discriminating elements associated with the animal production intensity (Table 1). However, more physiological details need to be added to better support this behavior.

The behavior observed in the Experiment 3 (Table 5) showed itself to be similar to the aspects observed in the Experiment 1. The high discriminatory capacity associated to the BNI (Table 2) allowed verify the significance associated with the principal effects of factorial arrangement.

From the results obtained in the Experiment 4 (Table 6), a discussion about other aspects related to BNI estimation and interpretation becomes necessary. As it can be seen from Table 6, the behavior of BNI was inverse from that observed in other trials, that is, the greatest BNI estimate indicated the least productive efficiency.

In heuristic terms, the linear combination of intake and production equalized from the MANOVA information has the objective of maximizing the discrimination among the experimental groups (Harris, 1975). Assuming this, it can be verified that the index generated by the linear combination cannot be considered, in any situation, an absolute comparison measurement since such value is dependent on the behavior and structure of the evaluated data. Therefore, variations in dimension and dispersion of intake and production variables as well as in the discrimination power among the groups shown for each of these variables will influence directly the new variable dominium. However, the maximum intra-experimental discrimination is guaranteed.

Thus, inversions in the direction and differences in the BNI modulus are common; however, they do not disqualify the obtained inferences because its use has an exclusive discrimination aim. In this context, it should be pointed out that the BNI should be seen only as a discriminatory index and never as an absolute measure of the productive efficiency. In this situation, the maintenance of either FCR or FEI plus BNI will identify more clearly the new variable direction and will provide, yet under the light of the experimental methodologies adopted an inter-experiment confrontation element.

However, it is important to consider that the inferences should be preferably based on the BNI, because it gives more statistical security in the identification of the most efficient groups, treatments or factor levels.

On the other hand, the variation of values and modulus of BNI from different data sets was the reason for it not been called bio-nutritional efficiency (Euclides Filho et al., 2001) in this work. The efficiency term should be used when a mathematical scale and reference values for comparison among groups or experiments are defined. Therefore, the mathematical inter-experimental variation of the first canonical variable does not characterize a true efficiency value, but only a discriminatory index.

Furthermore, the results shown in Table 6 indicated that even obtaining similar inference from analysis of variance based on FEI, FCR and BNI, the discriminatory power of this last index is also observed in additional statistical procedures. In this way, among the genetic groups evaluated, the discrimination by multiple comparisons based on FCR and FEI allowed the identification of two groups whereas three groups were distinguished from the information provided by BNI (Table 6).

The results obtained in Experiment 5 (^{Table 7}) once more emphasize the high discriminatory power associated with the BNI. This was already observed in the results of Experiments 1, 2 and 4. The use of FCR and FEI did not imply in a detection of a significant result associated with the different orthogonal contrasts. However, applying the BNI approach allowed not only to differentiate the roughage sources (corn silage versus sugar cane) but also to detect a quadratic effect related to the replacement of sugar cane with cottonseed (^{Table 7}).

Conclusions

The feed conversion ratio and feed efficiency index do not provide similar inference about efficiency of animal production and may compromise experimental conclusion.

Conversely, the use of the first canonical variable, called bio-nutritional index, guarantees the maximum discrimination among the experimental groups.

Furthermore, the bio-nutritional index concept showed to be broader than those applied to the feed conversion ratio or feed efficiency index because it also incorporates elements related to the animal production intensity. Thus, the application of this index is recommended with the objective of discriminate experimental groups in relation to the animal production efficiency.

Acknowledgments

The authors would like to thanks Professors José Fernando Coelho da Silva (UENF), Ricardo Ferreira Garcia (UENF), and Renato Ribeiro de Lima (UFLA), and the post-graduate student Jathinder Singh. Multani (UENF) for translating and providing technical suggestions in preparing the manuscript.

To Marcelo, dear friend. God bless your soul.

Literature Cited

Recebido em: 08/03/05

Aceito em: 06/07/05

• ANDREOTTI, M.O. Valor nutricional de diferentes fontes lipídicas para frangos de corte Jaboticabal:Universidade Estadual Paulista, 2002. 74p. Tese (Doutorado em Zootecnia) - Universidade Estadual Paulista, 2002.
• CRAMPTON, E.W. Analysis of the comparative feeding trial by the variance and covariance methods. Journal of Nutrition, v.7, p.305-319, 1934.
• CRUZ, C.D.; REGAZZI. A.J. Modelos biométricos aplicados ao melhoramento genético Viçosa, MG: Universidade Federal de Viçosa, 2001. 390p.
• EUCLIDES FILHO, K.; EUCLIDES, V.P.B.; FIGUEIREDO, G.R. et al. Eficiência bionutricional de animais nelore e seus mestiços com simental e aberdeen angus, em duas dietas. Revista Brasileira de Zootecnia, v.30, p.77-82, 2001.
• EUCLIDES FILHO, K.; FIGUEIREDO, G.R.; EUCLIDES, V.P.B. et al. Eficiência bionutricional de animais da raça nelore e seus mestiços com caracu, angus e simental. Revista Brasileira de Zootecnia, v.31, p.331-334, 2002.
• FISHER, R.A. The use of multiple measurements in taxonomic problems. Annals of Eugenics, v.7, p.179-188, 1936.
• FISHER, R.A. The statistical utilization of multiple measurements. Annals of Eugenics, v.8, p.376-386, 1938.
• FONSECA, J.S.; MARTINS, G.A. Curso de estatística São Paulo: Editora Atlas, 1982. 286p.
• GESUALDI JR., A.; QUEIROZ, A.C.; RESENDE, F.D. et al. Desempenho produtivo de bovinos nelore e caracu selecionados para peso aos 378 dias de idade e nelore comum. In: REUNIÃO ANUAL DA SOCIEDADE BRASILEIRA DE ZOOTECNIA, 40., 2003, Santa Maria. Anais...Santa Maria: Sociedade Brasileira de Zootecnia, 2003 (CD-ROM/Seção de Nutrição de Ruminantes).
• GUIDONI, A.L. Alternativas para comparar tratamentos envolvendo o desempenho nutricional animal Piracicaba: Escola Superior de Agricultura "Luiz de Queiroz", 1994. 105p. Tese (Doutorado em Agronomia) - Escola Superior de Agricultura "Luiz de Queiroz", 1994.
• HARRIS, R.J. A primer of multivariate statistics New York: Academic Press, 1975. 332p.
• JOHNSON, R.A.; WICHERN, D.W. Applied multivariate statistical analysis New Jersey: Prentice Hall, 1998. 816p.
• RESENDE, F.D.; NARDON, R.F.; RAZOOK, A.G. et al. Desempenho e características de carcaça de zebuínos e caracu selecionados para peso aos 378 dias de idade, submetidos a dois níveis de energia na terminação. In: REUNIÃO ANUAL DA SOCIEDADE BRASILEIRA DE ZOOTECNIA, 37., 2000, Viçosa, MG. Anais... Viçosa, MG: Sociedade Brasileira de Zootecnia, 2000 (CD-ROM, Seção Oral, Nutrição de Ruminantes, arquivo 0507).
• SEARLE, S.R. Matrix algebra for the biological sciences New York: John Willey & Sons, 1966. 296p.
• SOUSA, D.P.; CAMPOS, J.M.; VALADARES FILHO, S.C. et al. Produção e composição do leite de vacas alimentadas com silagem de milho ou cana-de-açúcar parcialmente substituída por caroço de algodão. In: REUNIÃO ANUAL DA SOCIEDADE BRASILEIRA DE ZOOTECNIA, 39, 2002, Recife. Anais... Recife: Sociedade Brasileira de Zootecnia, 2002 (CD-ROM, arquivo 06sbz821).
• VITTORI, A.; QUEIROZ, A.C.; RESENDE, F.D. et al. Desempenho e características de carcaça de animais Zebu e Caracu castrados e não castrados. In: REUNIÃO ANUAL DA SOCIEDADE BRASILEIRA DE ZOOTECNIA, 38, 2001, Piracicaba. Anais... Piracicaba: Sociedade Brasileira de Zootecnia, 2001. p.580-582.
• WEILL JR., W.B. Adjustment for size - a possible misuse of ratios. American Journal of Clinical Nutrition, v.11, p.249-252, 1962.

*

(in memoriam)

Publication Dates

• Publication in this collection
  23 Feb 2006
• Date of issue
  Dec 2005

History

• Received
  08 Mar 2005
• Accepted
  06 July 2005