Modelos de cointegração com um ou dois limiares: uma aplicação para o preço do frango inteiro resfriado em mercados atacadistas no Brasil

Modelos de cointegração com um ou dois limiares: uma aplicação para o preço do frango inteiro resfriado em mercados atacadistas no Brasil¹

Leonardo Bornacki de Mattos^I; João Eustáquio de Lima^II; Viviani Silva Lirio^III; Antônio Carvalho Campos^IV

^IProfessor Adjunto do Departamento de Economia Rural da Universidade Federal de Viçosa. E-mail: [e-mail]

^IIProfessor Titular do Departamento de Economia Rural da Universidade Federal de Viçosa. E-mail: [e-mail]

^IIIProfessora Associada do Departamento de Economia Rural da Universidade Federal de Viçosa. E-mail: [e-mail]

^IVProfessor do Departamento de Economia Rural da Universidade Federal de Viçosa. E-mail: [e-mail]

RESUMO

A maioria dos estudos de integração de mercados que utiliza a técnica de cointegração com threshold não se preocupa em testar qual o número de regimes de ajustamento de preços é o mais adequado. Neste estudo, utiliza-se um procedimento para determinar o número de regimes estatisticamente indicado para diferentes mercados regionais de carne de frango no Brasil, no período de janeiro de 1998 a junho de 2007. Os resultados mostram que, para um grupo de mercados, o modelo com dois regimes é o mais indicado, enquanto para os demais mercados, o modelo com três regimes é o que melhor se ajusta. Constata-se a presença de significativas barreiras à transmissão de choques de preços entre os mercados, o que provavelmente resulta de custos de transação não desprezíveis na comercialização da carne de frango.

Palavras-chaves: Integração de mercados, cointegração com threshold, custos de transação, teste de linearidade, carne de frango.

ABSTRACT

Most studies about market integration that use threshold cointegration do not usually test the number of regimes of price adjustment. In this study, we use a testing procedure to determine the number of statistically significant regimes for regional markets of poultry in Brazil in the period of January 1998 to June 2007. Results show that, for some markets, two regimes are adequate, whereas for others, the model should have three regimes. We also conclude that there are important barriers to price transmission among the markets which may come from the existence of high transaction costs regarding trades involving poultry.

Key-words: market integration, threshold cointegration, transaction costs, linearity test, poultry.

Classificação JEL: F15; C32.

1. Introdução

Os primeiros estudos que testaram a integração de mercados se basearam nas correlações entre os preços para descrever a maneira com que os mercados são relacionados, o que confere um caráter estático às análises. O modelo proposto por Ravallion (1986), ao incorporar as defasagens temporais das séries de preços, foi o primeiro a considerar o caráter dinâmico do processo de ajustamento dos preços. Desde então, os procedimentos de testes apresentaram várias sofisticações, culminando na ampla utilização das técnicas de cointegração.

Entre os modelos desenvolvidos a partir das técnicas de cointegração, os modelos vetoriais de correção de erro (VEC) têm sido os mais utilizados. Entretanto, ao se usar um modelo VEC, há uma pressuposição implícita. Os ajustamentos de preços, que são induzidos por desvios do equilíbrio de longo prazo, são considerados uma função contínua e linear de tal desvio. Mesmo desvios muito pequenos conduziriam a um processo de ajustamento em cada mercado.

Os custos de transação dificultam a comercialização. Isto gera faixas nas quais os ajustamentos de preços ocorrem com diferentes intensidades, a depender da magnitude desses custos. Essas faixas são denominadas regimes, que são delimitados por limiares (thresholds)².

Recentemente, o reconhecimento da importância de custos de transação, quase sempre negligenciados, tem levado à aplicação de novas metodologias que explicitamente reconhecem a influência de tais custos sobre a ligação econômica entre mercados espacialmente separados.

A classe dos modelos autorregressivos com threshold (TAR models) tem ocupado posição de destaque na literatura especializada em análises de integração de mercados. Nessa classe de modelos, as observações que compõem a amostra são divididas em grupos, ou regimes, e o critério adotado para tal divisão é o valor assumido por determinada variável, que é conhecida como variável de threshold. A cada um dos grupos corresponde uma autorregressão. Os modelos autorregressivos (AR) tradicionais, incorporados da variável de threshold, dão origem aos autorregressivos não lineares, denominados TAR models, em que a inicial "T" se refere à presença do threshold.

Entre as técnicas derivadas da classe dos modelos TAR, a cointegração com threshold (Threshold Cointegration), inicialmente proposta por Balke e Fomby (1997), tem sido a mais utilizada, sobretudo na literatura internacional³. No Brasil, embora existam várias pesquisas sobre integração de mercados, apenas o estudo de Mattos et al. (2009), que analisou a integração dos mercados de boi gordo nos estados de Minas Gerais e São Paulo, utilizou modelos de cointegração com threshold.

Entretanto, como ressaltado por Meyer (2004), a maioria dos estudos que utilizam a cointegração com threshold, inclusive o de Mattos et al. (2009), não se preocupa em testar se o número de regimes adotado nas análises é de fato o mais adequado. Modelos cujo número de regimes seja determinado a partir de testes apropriados devem apresentar resultados estatisticamente mais satisfatórios.

Neste estudo, utiliza-se o procedimento proposto por Lo e Zivot (2001) para determinar o número de regimes de ajustamento de preços em cada um dos modelos de cointegração com threshold estimados para a análise de integração dos mercados regionais de carne de frango no Brasil, no período de janeiro de 1998 a junho de 2007.

O procedimento desenvolvido por Lo e Zivot (2001), ao contrário do adotado por Mattos et al. (2009), permite a análise de assimetrias no processo de transmissão de preços, além de utilizar um método de simulação para aproximação da distribuição assintótica da estatística de teste da hipótese de linearidade, o que se apresenta como outro importante avanço em relação ao estudo de Mattos et al. (2009).

Há de se ressaltar, também, a importância dos mercados de carne de frango para o agronegócio no Brasil. A carne de frango representa cerca de 50% das exportações brasileiras de carnes, percentual esse superior ao das carnes bovina (38,4%) e suína (9,2%). Em 2007, o Brasil respondeu por cerca de 15% da produção mundial de carne de frango, atrás apenas dos Estados Unidos (23,9%) e da China (17%). Nesse mesmo ano, o Brasil manteve-se como o maior exportador mundial de carne de frango, participando de 45% das vendas destinadas ao mercado internacional⁴.

Além dessa Introdução, este estudo inclui outras quatro seções. Na seção 2, apresenta-se uma breve revisão da literatura, com o objetivo de apontar os critérios adotados em alguns dos principais estudos de integração de mercados para definição do número de regimes. Na seção 3, apresentam-se o modelo analítico, o modelo empírico, o procedimento de estimação e os dados utilizados na análise da integração dos mercados regionais de carne de frango no Brasil. Na seção 4, são apresentados os resultados obtidos. A seção 5, reservada às conclusões, finaliza o estudo.

2. Revisão de literatura

O estudo de Goodwin e Holt (1999) foi um dos primeiros a utilizar a técnica de cointegração com threshold, desenvolvida por Balke e Fomby (1997), para análises empíricas de integração de mercados. A principal contribuição do estudo de Goodwin e Holt (1999) foi o fato de considerarem a possibilidade de os processos de transmissão de preços serem não lineares, o que ainda não havia sido feito. Esses autores estimaram modelos de correção de erros com threshold (modelos TVEC), com três regimes de ajustamento de preços, para investigar de que modo choques de preços são transmitidos entre produtor, atacado e varejo na cadeia de carne bovina nos Estados Unidos. Os autores não utilizaram nenhum procedimento estatístico para a definição do número de regimes. A partir de então, muitos outros estudos passaram a utilizar a cointegração com threshold para análises de integração de mercados.

Goodwin e Piggott (2001) analisaram a relação entre os preços em vários mercados regionais de milho e soja na Carolina do Norte, Estados Unidos. Esses autores, assim como Goodwin e Holt (1999), utilizaram autorregressões com três regimes sob a justificativa de que essa especificação possibilita a análise de assimetrias no processo de ajustamento de preços. Entretanto, nenhum teste foi realizado para confirmar se essa especificação é, estatisticamente, a mais indicada.

Outro estudo que ocupou posição de destaque foi o realizado por Lo e Zivot (2001), que pesquisaram a natureza não linear do ajustamento à Lei do Preço Único. Esses autores desenvolveram uma sistemática para especificação, teste e estimação do ajustamento à Lei do Preço Único.

O procedimento adotado por Lo e Zivot (2001) foi similar ao de duas etapas sugerido por Balke e Fomby (1997), com a diferença de que os primeiros autores concentraram-se em procedimentos de estimação e de testes multivariados. Lo e Zivot (2001) ainda acrescentaram uma terceira etapa na análise, que procurou avaliar a especificação dos modelos com threshold a partir de testes de hipóteses baseados em modelos aninhados, conforme o estudo de Hansen (1999). A metodologia desenvolvida foi empregada na análise de cointegração com threshold para uma gama muito grande de preços de 41 bens e serviços, em 29 cidades dos Estados Unidos.

Sephton (2003) procurou estender a análise de Goodwin e Piggott (2001) em algumas direções, por considerar que a análise realizada por aqueles autores está sujeita a potenciais erros de especificação⁵. Sephton (2003) considerou importante determinar se o teste multivariado de cointegração com threshold proposto por Hansen e Seo (2002) confirmaria os resultados obtidos por Goodwin e Piggott (2001). Sephton (2003) adotou o teste univariado de Hansen (1999) para determinar o número de regimes nos modelos de cointegração com threshold estimados. Os resultados indicaram que a especificação com dois regimes é a mais indicada para a base de dados utilizada.

Meyer (2004) estudou os efeitos dos custos de transação sobre a integração espacial dos mercados de suínos na Alemanha e na Holanda, a partir de um modelo de cointegração com threshold com dois regimes. Esse autor ressaltou que, na maior parte dos estudos que utilizaram essa técnica, não foi apresentada nenhuma justificativa para o número de thresholds adotado. Embora Meyer (2004) tivesse apresentado uma discussão sobre o número de regimes a ser considerado, não realizou nenhum teste estatístico para tal finalidade.

Ben-Kaabia et al. (2005) estudaram o mecanismo de transmissão de preços na cadeia produtiva de aves na Espanha, caracterizada por elevado grau de integração vertical e forte concentração horizontal, a partir de modelos TVEC com três regimes. O número de regimes foi determinado por meio do procedimento proposto por Lo e Zivot (2001). Ben-Kaabia et al. (2005) analisaram tanto a relação entre os preços da ração e os preços pagos aos produtores de aves, como a relação entre os preços pagos aos produtores e aqueles observados no varejo.

3. Metodologia

3.1. Cointegração com threshold

O estudo de cointegração com threshold foi inicialmente desenvolvido por Balke e Fomby (1997) como meio de combinar cointegração e não linearidade. Esta última é atribuída à presença de custos de transação. No contexto de cointegração, choques que perturbam o equilíbrio de longo prazo são corrigidos pelo sistema por meio do Mecanismo de Correção de Erros (MCE), que influencia o comportamento de curto prazo das variáveis de modo a existir uma relação entre as dinâmicas de curto e longo prazos.

Dois mercados hipotéticos, a e B, por exemplo, estarão em equilíbrio de longo prazo se houver uma combinação linear entre os seus respectivos preços, P_tª e P_t^B, tal que:

em que

sendo um termo de erro ruído branco.

A análise da relação de equilíbrio entre P_tª e P_t^B recai sobre a natureza do processo Z_t, que representa o desvio da relação de equilíbrio de longo prazo, apresentada em (1). Se, em Z_t = ρ Z_{t -1} + E_t , o coeficiente autorregressivo de primeira ordem (ρ) for tal que ρ = 1, Z_t segue um passeio aleatório, que é não estacionário. Nesse caso, P_tª e P_t^B não são cointegrados e não há relação de equilíbrio de longo prazo entre os preços⁶. Entretanto, se ρ< 1, o processo Z_t é estacionário, de modo que os preços são cointegrados e apresentam relação de equilíbrio de longo prazo.

A incorporação dos efeitos dos custos de transação fornece uma justificativa para o uso de modelos de ajustamento de preços com a inclusão de uma variável threshold. Nesse tipo de modelo, a extensão em que desvios do equilíbrio de longo prazo são responsáveis por ajustamento de preços depende da magnitude de tal desvio. O processo de ajustamento pode ser diferente, caso o desvio esteja acima ou abaixo de um valor específico, ou seja, de um threshold. Tal situação é ilustrada na Figura 1.

A Figura 1(a) ilustra o processo de ajustamento de preços (ΔP_t) como função linear dos desvios do equilíbrio de longo prazo, equivalentes ao termo de correção de erro (Z _t-1), e corresponde ao uso de um modelo VEC sem o efeito threshold.

A Figura 1(b) ilustra o processo de ajustamento de preços correspondente a um modelo TVEC com um único threshold (γ₁). Desvios do equilíbrio de longo prazo, inferiores a γ₁, conduzem a um processo de ajustamento, delimitado pelo regime 1, diferente do processo de ajustamento induzido por desvios superiores a γ₁ (regime 2). Segundo Meyer (2004), essa especificação pode ser adequada quando se espera que o ajustamento ocorra em uma única direção, sendo transmitidos ou choques positivos ou choques negativos de preços.

A Figura 1(c) ilustra um modelo de ajustamento com três regimes. Um deles está abaixo do termo de equilíbrio de longo prazo (regime 3), e outro, acima (regime 1). A região entre e γ₁ (regime 2) pode ser interpretada como os desvios do equilíbrio de longo prazo, que são tão pequenos comparados aos custos do ajustamento, que possivelmente não induzirão ajustamento nos preços relativos, ou seja, uma região de "não ajustamento", em que os preços não são cointegrados. Além disso, um modelo com dois thresholds é consistente com desvios tanto positivos quanto negativos em relação ao equilíbrio de longo prazo. Essa especificação permite, portanto, a investigação de assimetrias, uma vez que a dinâmica induzida por choques negativos pode ser comparada àquela provocada por choques positivos.

Embora um modelo com três regimes seja mais flexível e apresente maior facilidade para interpretação dos resultados quando comparado a um modelo com dois regimes, não há, na literatura especializada, indicação de que o primeiro seja superior ao segundo. Os estudos de Hansen (1999) e Lo e Zivot (2001) sustentam que a definição deve seguir critérios estatísticos, devendo ser adotada a especificação que melhor se ajusta à base de dados utilizada. Os resultados dos testes estatísticos propostos por esses autores podem, inclusive, indicar que a melhor especificação é a de um modelo com um único regime, sem nenhum threshold, como aquele apresentado na Figura 1(a).

3.2. Modelo Empírico: especificação, estimação e teste do número de regimes

Neste estudo, os procedimentos propostos por Lo e Zivot (2001) são adotados para determinar, estatisticamente, o número adequado de regimes em modelos bivariados de cointegração com threshold. O procedimento requer a estimação de modelos referentes a três especificações a serem testadas: modelo vetorial de correção de erros com um único regime (VEC); modelo vetorial de correção de erros com dois regimes (TVEC₂); e modelo vetorial de correção de erros com três regimes (TVEC₃). Os modelos a serem estimados seguem as seguintes especificações:

Modelo VEC:

Modelo TVEC₂:

Modelo TVEC₃:

em que, em (3),(4) e (5): P_t é o vetor dos logaritmos naturais dos preços em cada um dos dois mercados; Δ é o operador de primeira diferença; µ^{( j )} são vetores-coluna (2 x 1) de termos constantes; Γ^{( j )} (i = 1,2,...) são matrizes (2 x 2) de parâmetros; α ^(j) são vetores-coluna (2 x 1) dos coeficientes de ajustamento; Z_t-1 são os desvios da relação de equilíbrio de longo prazo entre os pares de preços, defasados em um período, utilizados como termo de correção de erro; u_t^(j), v_t^(j) e ε_t^(j) são vetores-coluna (2 x 1) dos termos de erro; k indica o número de defasagens do vetor P_t; j=1, 2 e 3 indica o regime de ajustamento dos preços; e γ₁e γ₂ são os parâmetros de threshold que delimitam os diferentes regimes de ajustamento de preços.

Lo e Zivot (2001) combinam o método de estimação de modelos autorregressivos univariados com threshold (TAR models), com dois e três regimes, desenvolvido por Hansen (1999), com a estratégia adotada por Tsay (1998) para a estimação de modelos autorregressivos multivariados com threshold (TVAR models). O procedimento completo, que envolve a estimação e o teste da significância estatística do efeito threshold, é realizado em três etapas principais.

A primeira etapa corresponde a testes de raízes unitárias para se identificar a ordem de integração das séries de preços. Posteriormente, procura-se verificar se os pares de preços são cointegrados. A hipótese nula de não cointegração é testada contra a hipótese alternativa de cointegração linear, ou seja, sem o efeito threshold.

A segunda etapa consiste na obtenção dos parâmetros de threshold, que determinam os limites entre os diferentes regimes de ajustamento de preços. A determinação dos parâmetros γ₁ e γ₂ segue o procedimento proposto por Balke e Fomby (1997) e aprimorado por Lo e Zivot (2001). Inicialmente, ordenam-se os dados de acordo com o valor da variável de threshold, ou seja, Z_t-1, em vez de ordená-los através do tempo, dando origem ao que é conhecido na literatura como uma autorregressão "ordenada", que é útil devido ao fato de o modelo TVEC ter sua estrutura alterada de acordo com o valor Z_t-1.

Posteriormente, seguindo Lo e Zivot (2001), os parâmetros γ₁ e γ₂ são obtidos de maneira a solucionar o seguinte problema de minimização:

em que:

e é a matriz de covariâncias dos resíduos do modelo TVEC com j regimes.

A minimização de (7) é feita por meio de um procedimento padrão, que consiste na construção do que é conhecido na literatura especializada como "grade de busca bidimensional", dado que S_j(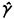₁,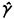₂) não é diferenciável em γ₁ (i=1,2). Num eixo horizontal, são plotados os valores referentes ao parâmetro a ser obtido, γ₁ ou γ₂, e, num eixo vertical, os valores referentes à variável a ser minimizada. A partir de então, são realizadas estimações sequenciais do modelo TVEC, condicionadas aos diferentes valores assumidos pelo parâmetro γ₁, até que S_j (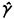₁,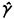₂)seja minimizada.

No procedimento adotado para determinação de

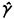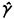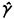₁, são consideradas apenas as observações para as quais Z_t-1< 0, enquanto para a busca de ₂, apenas as observações para as quais Z_t-1> 0⁷. Depois de encontrados os parâmetros de threshold, os modelos TVEC especificados em (4) e (5) são estimados pelo método dos Mínimos Quadrados Ordinários de maneira condicional aos valores de ₁e ₂.

A terceira etapa realizada na estimação dos modelos TVEC consiste em testar o número adequado (estatisticamente) de regimes. A adoção de tal procedimento neste estudo visa superar um dos pontos críticos observados em grande parte dos estudos de cointegração com threshold. Segundo Meyer (2004), a maioria desses trabalhos não se preocupa em testar se o número de regimes considerado é de fato o mais adequado.

O procedimento consiste em, inicialmente, testar a hipótese nula de linearidade contra a hipótese alternativa de não linearidade com três regimes, por meio da estatística LR₁₃ proposta por Lo e Zivot (2001):

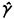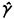em que (₂) e ₃ (₁, 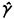₂) são as matrizes de covariâncias dos resíduos dos modelos VEC (linear) e TVEC₃, respectivamente, e T é o tamanho da amostra. A rejeição da hipótese de linearidade indica que o processo de ajustamento de preços é mais bem descrito por um modelo não linear, comparativamente aos tradicionais modelos VEC lineares. Não se pode, entretanto, afirmar que o modelo TVEC₃ é o mais adequado.

A definição do número exato de regimes deve, segundo Lo e Zivot (2001), ser feita em um procedimento adicional, no qual um modelo TVEC₃ é comparado a um TVEC₂. Essa argumentação tem como ponto de partida o estudo de Hansen (1999), onde são propostos testes sequenciais baseados em modelos aninhados, envolvendo, portanto, a estimação de modelos autorregressivos com threshold (TAR) restritos e irrestritos.

Lo e Zivot (2001) argumentam que, ao ser rejeitada a hipótese nula de linearidade, deve ser testada a hipótese de um modelo com dois regimes (TVEC₂) contra a alternativa de um modelo com três regimes (TVEC₃), para o que os autores propõem o uso da estatística LR₂₃:

em que

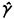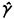₂ (₂) e ₃ (₁, 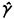₂) são as matrizes de covariâncias dos resíduos dos modelos TVEC₂ e TVEC₃, respectivamente.

Ocorre que, como ressaltado por Lo e Zivot (2001), as distribuições assintóticas das estatísticas LR₁₃ e LR₂₃ são não convencionais, uma vez que envolvem parâmetros que estão presentes apenas sob as hipóteses alternativas. Nesse caso, métodos de bootstrap devem ser utilizados para que os p-valores possam ser computados. Lo e Zivot (2001) adaptaram, para análises multivariadas, o algoritmo utilizado por Hansen (1999) para o caso univariado. O algoritmo para o bootstrap é o seguinte:

1. Gera-se uma amostra aleatória (t = 1, 2,... ), por amostragem com reposição, para o vetor dos resíduos _t obtidos na estimação do modelo VEC linear.

2. Gera-se, recursivamente, o vetor bivariado (t = 1, 2,... ) de preços, usando os parâmetros obtidos na estimação do modelo VEC linear.

3. Com o vetorsimulado, calcula-se a estatística LR* utilizando o mesmo método empregado para o cálculo de LR.

4. Repetem-se as etapas anteriores n vezes⁸.

5. Considera-se como p-valor de bootstrap o percentual da estatística LR*(simulada) que excede o LR(observado).

3.3. Descrição e fonte dos dados

Neste estudo, são utilizadas séries de preços diários do frango inteiro resfriado no mercado atacadista, uma vez que a arbitragem espacial, que é o fator que conduz os mercados regionais à integração, ocorre nesse nível.

Na cadeia agroindustrial da carne de frango, a função do atacadista é exercida pelo próprio produtor, que são as empresas processadoras da carne. Na outra ponta do canal de distribuição está o varejo. No tocante à carne de frango, as atividades de varejo são desempenhadas, na maior parte dos casos, pelos supermercados⁹. Portanto, assume-se como "preço no atacado" aquele estabelecido no processo de negociação entre as empresas processadoras e os supermercados¹⁰.

Foram consideradas as praças que apresentam maior potencial de comercialização e para as quais existem dados disponíveis da carne de frango resfriado no mercado atacadista: São Paulo (SP), Descalvado (SP), Porto Alegre (RS), Litoral Catarinense (SC), que inclui os municípios de Itajaí e Florianópolis, Oeste Paranaense (PR), que inclui as cidades de Toledo, Cascavel, Palotina e Medianeira, Ponta Grossa (PR), Belo Horizonte (MG), Goiânia (GO), Fortaleza (CE), Recife (PE) e Belém (PA). Em conjunto, os estados dessas praças respondem por cerca de 90% da produção de carne de frango no Brasil.

Os dados, considerados nos seus logaritmos naturais, são de periodicidade diária e cobrem o período para o qual são disponíveis, de 2 de janeiro de 1998 a 20 de junho de 2007, totalizando 2.339 observações. A fonte dos dados é a Consultoria Safras & Mercado (http://www.safras.com.br).

Aos sábados, domingos e feriados, não há coleta de dados. Assim, a série temporal é formada a partir do "empilhamento" das observações referentes aos preços coletados de segunda a sexta-feira. Faz-se necessário assumir a hipótese de que a variação de preços entre dois dias consecutivos, como por exemplo, terça e quarta-feira, quinta e sexta-feira, etc., é sistematicamente igual à variação que ocorre entre sexta e a segunda-feira seguinte. Embora essa seja uma limitação do estudo, imposta pelo uso de dados diários, a opção por dados semanais ou mensais reduziria significativamente o número de observações, resultando em limitação ainda maior. A estimação de modelos autorregressivos, sobretudo com mais de um regime, requer um número elevado de observações devido à perda de graus de liberdade referente ao elevado número de parâmetros a serem estimados.

4. Resultados e discussão

Inicialmente foi feita a determinação da ordem de integração das variáveis a partir do teste de raiz unitária de Dickey-Fuller Aumentado (ADF). Os resultados apontaram que todas as séries são integradas de primeira ordem, ou seja, I(1).

A análise de cointegração requer, previamente, a determinação do mercado central formador de preços. A escolha do mercado que apresenta o maior volume de comercialização conduziria às praças localizadas no estado do Paraná, maior produtor de carne de frango, segundo dados do Anualpec (2007)¹¹, e no estado de São Paulo, onde se concentra a maior parcela de estabelecimentos supermercadistas do País. A favor do estado de São Paulo está o fato de o segmento supermercadista ter posição privilegiada nas negociações com as empresas produtoras.

Em complemento ao critério de maior volume de comercialização, seguindo Asche et al. (1999), realizou-se teste de exogeneidade fraca. Os resultados apontaram a praça da cidade de São Paulo como fracamente exógena, o que ratificou a escolha do mercado de maior volume de comercialização como formador de preços.

Identificado o mercado central, testou-se, a partir dos testes de cointegração propostos por Engle e Granger (1987) e Johansen (1988), a cointegração entre os dez pares formados pelos preços praticados em São Paulo e em cada um dos demais dez mercados considerados na análise. Os resultados de ambos os testes indicaram que os preços em todas as praças, com exceção de Fortaleza, são cointegrados com o preço em São Paulo. Em função desses resultados Fortaleza foi excluída da análise.

Obtidas as relações de cointegração e seus respectivos resíduos, deu-se prosseguimento à estimação dos modelos VEC, TVEC₂ e TVEC₃ especificados nas equações (3), (4) e (5), respectivamente. Em seguida, foram realizados os testes para definição do número adequado de regimes. Inicialmente, testou-se, através do teste de linearidade (estatística LR₁₃), a hipótese nula de um único regime (modelo VEC) contra a hipótese alternativa de três regimes (modelo TVEC₃). Os resultados são apresentados na Tabela 1.

Quanto à análise de significância estatística do efeito threshold, conclui-se, a partir das estatísticas LR₁₃ presentes na Tabela 1, que a hipótese nula de linearidade apenas não pode ser rejeitada para o mercado do Litoral Catarinense, para o qual a especificação linear (VEC) é mais adequada que a não linear imposta pelo TVEC₃. Para todos os demais mercados, entretanto, conclui-se que os modelos não lineares são os que melhor se ajustam aos dados, uma vez que a hipótese nula pode ser rejeitada nos níveis de significância de 1%, 5% ou 10%.

Uma vez confirmada a significância estatística do efeito threshold, torna-se relevante determinar, para o caso específico dos dados utilizados, se um modelo com dois regimes é estatisticamente mais adequado do que um com três, o que é feito a partir da estatística LR₂₃. Se esse for o caso, a estatística deve indicar a não rejeição da hipótese nula de um TVEC₂ contra a hipótese alternativa de um TVEC₃. Os resultados obtidos são apresentados na Tabela 1.

Os resultados indicam que a hipótese nula pode ser rejeitada, a 1%, apenas para a praça de Belo Horizonte. Nesse nível, portanto, os modelos TVEC₂ são mais adequados que os modelos TVEC₃ para todas as demais praças. Para os mercados de Belém, Descalvado, Oeste Paranaense, Ponta Grossa e Litoral Catarinense, os valores obtidos para as estatísticas LR₂₃ indicam que a hipótese nula não deve ser rejeitada nem mesmo a 10% e, portanto, que o modelo TVEC₂ é mais adequado que o TVEC₃.

Quando considerado o nível de 5% para as praças de Goiânia, Porto Alegre e Recife, a estatística indica rejeição da hipótese de o modelo adequado ser o TVEC₂. Para essas praças, portanto, o número adequado de regimes depende do nível de significância assumido, 1% ou 5%. Adotando- se o nível de 5%, define-se que o modelo TVEC₂ é o mais indicado para as praças de Belém, Descalvado, Litoral Catarinense, Oeste Paranaense e Ponta Grossa, enquanto o modelo TVEC₃ é o que melhor se ajusta às praças de Belo Horizonte, Goiânia, Porto Alegre e Recife. É possível que uma faixa na qual os preços não respondam aos desvios do equilíbrio de longo prazo, tal como sugere um modelo TVEC₃, também exista para as praças nas quais a hipótese nula não pôde ser rejeitada. Entretanto, as informações contidas nos dados utilizados não são suficientes para detectar a existência dessa faixa.

Determinado o número de regimes para os diferentes mercados, passa-se a analisar as estimativas dos parâmetros de threshold, dos coeficientes de ajustamento e o teste de significância estatística da não linearidade, referentes aos modelos TVEC₂ e TVEC₃ estimados, cujos resultados são apresentados na Tabela 2.

Quanto aos resultados referentes aos modelos TVEC₂, verifica-se que as observações estão concentradas, com exceção da praça de Ponta Grossa, no regime 1. Para os mercados nos quais 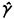₁ é positivo, o regime 1 inclui tanto os choques negativos, independentemente de suas magnitudes, quanto os choques positivos que são inferiores ao valor do parâmetro de threshold. Para esses mercados, no regime 2 estão apenas as observações relacionadas aos choques maiores que os valores de 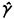₁. Uma vez que são esperados ajustamentos de preços em apenas uma direção, pode-se dizer que para todas as praças, exceto para Ponta Grossa, somente aumentos de preços em São Paulo são transmitidos entre os mercados. Os parâmetros de threshold, com a exceção de Descalvado, são elevados e ratificam a presença de significativos custos de transação, que provavelmente inviabilizam a arbitragem e, portanto, a transferência de produtos de um mercado a outro. Além disso, para todos esses mercados, os desvios do equilíbrio são eliminados a partir de ajustes nos preços das praças e não no valor do mercado central, o que é coerente com os resultados do teste de exogeneidade fraca, realizado para determinar o mercado central.

Entre as praças para as quais foram estimados modelos TVEC₂, Ponta Grossa é a única cujas observações não estão concentradas no regime 1. Esse resultado estabelece que, geralmente, os choques transmitidos entre os mercados estão associados a reduções de preços em São Paulo, que é o mercado central. Diferente do que ocorre com os demais mercados, esses choques são eliminados tanto por ajustes no preço dessa praça quanto por ajustes na cotação de São Paulo, o que põe em dúvida a exogeneidade de São Paulo em comparação à praça de Ponta Grossa. A proximidade de Ponta Grossa em relação à capital paulista, bem como o fato de essa praça estar localizada no estado responsável pelo maior volume de produção de carne de frango, podem explicar, pelo menos em parte, esse resultado.

A última coluna da Tabela 2 traz os resultados do teste de linearidade, a partir do qual é testada a hipótese nula de linearidade (VEC) contra a alternativa de não linearidade em dois regimes (TVEC₂). Como foi constatado, a hipótese nula pode ser rejeitada, a 1%, para Descalvado e Ponta Grossa; a 5%, para o Litoral Catarinense e o Oeste Paranaense; e, a 10%, para Belém.

Quanto aos modelos TVEC₃, os resultados referentes ao mercado de Belo Horizonte indicam que tanto os preços em São Paulo quanto em Belo Horizonte se ajustam a eventuais desequilíbrios, uma vez que os coeficientes de ajustamento, nos três regimes, são estatisticamente significativos. Não há uma faixa neutra, de maneira que mesmo os choques relativamente pequenos são transmitidos entre os mercados. Entretanto, os coeficientes de ajustamento são menores no regime 3, o que representa resposta mais lenta dos preços em ambos os mercados, quando os choques são positivos, ou seja, quando há reduções nos valores em São Paulo. Por outro lado, o maior coeficiente de ajustamento está no regime 1, o que indica que a elevação dos preços em São Paulo, superior a 3,2%, é rapidamente transmitida aos preços observados na capital mineira.

A região neutra é identificada para o mercado de Goiânia, onde o preço do frango inteiro resfriado se ajusta a desequilíbrios apenas quando há aumentos do preço em São Paulo (choques negativos) superiores a 1,7%. Quando o choque na relação de equilíbrio de longo prazo é positivo, não há resposta por parte do preço praticado na capital de Goiás. Vale ressaltar que a maior parcela das observações, cerca de 52%, se concentra no regime 2, no qual não há cointegração entre os preços. Outros 42% estão no regime 1, correspondentes à transmissão de aumentos de preço em São Paulo, enquanto apenas 6% estão no regime em que há transmissão de reduções de valor na capital paulista.

Os resultados referentes ao mercado de frango resfriado em Porto Alegre indicam que diminuições de preços em São Paulo, superiores a 11,3% do valor médio praticado na capital gaúcha, não são transmitidas entre as praças. Por outro lado, quando ocorrem aumentos em São Paulo superiores a 8,5%, apenas o preço em Porto Alegre se ajusta. As reduções e os aumentos de preços inferiores a esses percentuais são eliminados por ajustes em ambos os valores, embora os reduzidos coeficientes de ajustamento indiquem que tal ajuste requer tempo elevado.

Quanto ao mercado de frango inteiro resfriado em Recife, verifica-se que reduções de preço em São Paulo, mesmo maiores que 13,2% do preço médio dessa carne na capital pernambucana, não são transmitidas entre os mercados. Além do mais, nota-se que essa situação é a que ocorre com menor frequência. Na maior parte dos casos, os desequilíbrios, ou estão associados a aumentos de preços em São Paulo, que ultrapassam cerca de 1,5% do preço em Recife, quando apenas esse último mercado se ajusta, ou a choques, positivos e negativos, que são eliminados por meio de ajustes em ambos os preços.

5. Conclusões

Este estudo procurou determinar o número adequado de regimes de ajustamento de preços para os modelos utilizados na análise de integração dos mercados regionais de carne de frango no Brasil, no período de janeiro de 1998 a junho de 2007. Foram estimados modelos vetoriais de correção de erro com threshold, condicionados ao número de regimes determinado através de teste baseado em modelos aninhados.

Os procedimentos adotados indicaram São Paulo como o mercado central, a partir do qual choques de preços são transmitidos aos demais mercados regionais. Verificou-se, também, que o preço da carne de frango praticado na praça de Fortaleza não possui relação de equilíbrio de longo prazo com o preço praticado na capital paulista. Assim, com base nos dados utilizados na pesquisa, não é possível afirmar que Fortaleza faz parte do mercado interno desse tipo de carne.

Os testes utilizados para determinar o número adequado de regimes de ajustamento de preços definiram que o modelo TVEC₂ é o mais indicado para as praças de Belém, Descalvado, Litoral Catarinense, Oeste Paranaense e Ponta Grossa, enquanto o modelo TVEC₃ é o que melhor se ajusta aos valores referentes às praças de Belo Horizonte, Goiânia, Porto Alegre e Recife. É possível que a especificação com três regimes, cuja interpretação é mais intuitiva sob o ponto de vista econômico, também seja válida para o primeiro grupo de mercados. Entretanto, os dados disponíveis não permitiram detectá-la. O fato de a especificação indicada não ser a mesma para todas as praças analisadas ratifica a importância dos testes utilizados na determinação do número de regimes.

De maneira geral, os resultados indicam a presença de barreiras significativas à transmissão de choques de preços entre os mercados, o que provavelmente ocorre em função de custos inerentes ao processo de ajustamento, ou seja, custos de transação não desprezíveis na comercialização da carne de frango.

6. Referências Bibliográficas

• ANUALPEC 2007. Anuário da pecuária brasileira São Paulo: Instituto FNP, abr. 2007. 368 p.
• ASCHE, F.; BREMNES, H.; WESSELLS, C. R. Product aggregation, market integration, and relationships between prices: an application to world salmon markets. American Journal of Agricultural Economics, v. 81, n. 3, p. 568-581, august 1999.
• BALKE, N.S.; FOMBY, T.B. Threshold cointegration. International Economic Review, v. 38, n. 3, p. 627-645, Aug. 1997.
• BEN-KAABIA, M.; GIL, J.M.; AMEUR, M. Vertical integration and non-linear price adjustments: the Spanish poultry sector. Agribusiness, v. 21, n. 2, p. 253-271, 2005.
• ENGLE, R.F.; GRANGER, C.W. Co-integration and error-correction: representation, estimation and testing. Econometrica, v. 55, p. 251-276, 1987.
• GOODWIN, B.K.; HOLT, M.T. Price transmission and asymmetric adjustment in the U.S. beef sector. American Journal of Agricultural Economics, v. 81, n. 3, p. 630-637, Aug. 1999.
• GOODWIN, B.K.; PIGGOTT, N.E. Spatial market integration in the presence of threshold effects. American Journal of Agricultural Economics, v. 83, n. 2, p. 302-317, May 2001.
• HANSEN, B.E. Testing for linearity. Journal of Economic Surveys, v. 13, n. 5, p. 551576, 1999.
• HANSEN, B.E.; SEO, B. Testing for two-regime threshold cointegration in vector error-correction models. Journal of Econometrics, v. 110, n. 9, p. 293-318, 2002.
• JOHANSEN, S. Statistical analysis of cointegrating vectors. Journal of Economics Dynamics and Control, v. 12, p. 231-254, 1988.
• LO, M.C.; ZIVOT, E. Threshold cointegration and nonlinear adjustment to the law of one price. Macroeconomic Dynamics, v. 5, n. 4, p. 533-576, 2001.
• MATTOS, L. B.; LIMA, J. E.; LIRIO, V. S. Integração espacial na presença de custos de transação: um estudo para o mercado de boi gordo em Minas Gerais e São Paulo. Revista de Economia e Sociologia Rural, v. 47, n. 1, 2009.
• MEYER, J. Measuring market integration in the presence of transaction costs: a threshold vector error correction approach. Agricultural Economics, v. 31, n. 21, p. 327-334, 2004.
• RAVALLION, M. Testing market integration. American Journal of Agricultural Economics, v. 68, n. 1, p. 102-109, Feb. 1986.
• SEPHTON, P.S. Spatial market arbitrage and threshold cointegration. American Journal of Agricultural Economics, v. 85, n. 4, p. 1041-1046, Nov. 2003.
• TSAY, R.S. Testing and modeling multivariate threshold models. Journal of the American Statistical Association, v. 93, p. 1188-1202, 1998.

1

Artigo extraído da tese de doutorado do primeiro autor.

2

Explicação mais detalhada sobre o significado de "regimes" é apresentada na seção 3.1.

3

Alguns exemplos de estudos que fizeram opção por esse método são: Goodwin e Holt (1999), Goodwin e Piggott (2001), Lo e Zivot (2001), Sephton (2003), Meyer (2004), Ben-kaabia et al. (2005), entre outros.

4

Dados da Associação Brasileira dos Produtores e Exportadores de Frangos (Abef,

http://abef.com.br).

5

Em seu estudo, Sephton (2003) utilizou os mesmos dados que os usados por Goodwin e Piggott (2001).

6

Se

ρ

>Z_t, Z_t é uma série explosiva e, portanto, não estacionária.

7

Seguindo Goodwin e Holt (1999), a busca por

₁ é feita entre 5% e 95% dos maiores (em valores absolutos) termos

Z_t-1 negativos, e a busca por

₂, entre 5% e 95% dos maiores termos

Z_t-1 positivos.

8

Assim como Hansen (1999), adota-se

n = 2.000.

9

Referências feitas aos supermercados incluem, também, os hipermercados.

10

Normalmente, as negociações entre esses dois agentes estão associadas a quantidades significativas de carne de frango. Não há, entretanto, uma medida que estabeleça o limite a partir do qual as atividades passam a ser classificadas como atacadistas.

11

O Paraná respondeu por cerca de 22,2% da produção nacional de carne de frango em 2006.

Datas de Publicação

• Publicação nesta coleção
  07 Jul 2011
• Data do Fascículo
  Dez 2010