Free vibration response of a multilayer smart hybrid composite plate with embedded SMA wires

Free vibration response of a multilayer smart hybrid composite plate with embedded SMA wires

K. Malekzadeh^I; A. Mozafari^II; Faramarz Ashenai GhasemiIII,^*

^IDepartment of Structural Analysis and Simulation, Space research institute, Tehran-Karaj Highway, Post box: 13445-768, Tehran, IRAN

^IIDepartment of Mechanical Engineering, K. N. Toosi University of Technology, Vafadar East Ave, 4th Tehran pars Sq., Tehran, Iran

^IIIDepartment of Mechanical Engineering, Shahid Rajaee Teacher Training University (SRTTU), Lavizan, Postal Code 16788-15811,Tehran, Iran

ABTRACT

In this paper, free vibration response of a hybrid composite plate was studied. Effects of some geometrical, physical and material parameters on response of the composite plates embedded with shape memory alloy (SMA) wires were investigated, which have not been reported in the literature thus far. Some of these parameters included important factors affecting free vibration response of the smart hybrid composite plates. The SMA wires were embedded within the layers of the composite laminate. First-order shear deformation theory (FSDT) was utilized to obtain the governing equations of hybrid composite plates. Transverse shear and rotary inertia effects of the plate were taken into consideration. For simply-supported boundary conditions, systematic closed form solutions were obtained by Navier's technique. It was established that dynamic behavior of the smart hybrid composite plate depended on various parameters such as volume fraction, temperature dependent recovery stress and tensile pre-strain of SMA wires and aspect ratio of the laminated hybrid plate.

Keywords: Free vibrations, Smart hybrid composite, SMA wires, Recovery stress.

1 INTRODUCTION

Shape memory alloys (SMAs) are characterized by their large internal forces, unique ability of changing their material properties, wide range of operational temperature, excellent damping properties and high durability. Using shape memory alloys as fiber reinforcement gives numerous adaptive capabilities to structures (Zhang et al., 2006 and Ni et al., 2007), one of which is controlling motion and vibration of structures.

NOTATIONS

A_ij, B_ij, D_ij

matrices of extensional, coupling and bending stiffness

A_rs(t), B_rs(t), W_rs(t)

time dependent coefficients for Fourier transform

a, b, h

length, width and thickness of the plate

G₁₂, G₁₃, G₂₃

shear modulus in principal directions of composite plate

h^(p)

composite lamina thickness of the pth lamina

I

inertia moment of plate

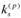
volume fraction of SMA wires of the pth lamina

k_s, k_c

volume fraction of SMA wires and composite medium

k_sh shear correction factor [K] symmetric stiffness matrix [M] symmetric mass matrix N, M tensile force and moment per unit length Nⁱ_x, Nⁱ_y tensile force per unit length in x and y direction N^r, M^r tensile recovery force and recovery moment per unit length N^T, M^T tensile thermal force and thermal moment per unit length Q_ij reduced stiffness matrices of the SMA hybrid composite reduced stiffness matrices of composite medium [Q^(p)_ij] reduced stiffness matrix of the lamina in the principal material coordinates q load function transformed reduced stiffness components u⁰, v⁰, w⁰ plate displacements in x, y and z directions at plate mid-plane Δ T temperature difference between current and reference temperatures. [T] transformation matrix α ^c(p) coefficient of thermal expansion of composite medium in the pth lamina α ^c_i(i=l,t) longitudinal and transverse thermal expansion coefficients of composite medium β ^(p) angle of SMA wires of the pth lamina θ ^(p) angle of fiber of the pth lamina γ₁₂, γ_13,γ₃₂ principal shear strains of plate γ_xy, γ_yz, γ_zx shear strains of plate in xy , yz and zx planes ε, χ; midplane strains and curvatures ε₁, ε₂ principal normal strains of the plate ε_xx, ε_y principal normal strains of the plate in the x, and y directions ε_xz, ε_yz shear strains of plate in xz, yz planes ν _ij Poisson's ratio in principal directions of composite plate ρ density of the whole plate ρ ₀ ^(p) density of the pth lamina of the plate σ₁, σ₂ principal normal stresses of plate σ_xz, σ_yz shear stresses of plate in xz, yz planes σ _r tensile recovery stress τ₁₂, τ₁₃, τ₂₃ principal shear stresses of plate ψ_x, ψ_y shear rotations in the x and y directions ω _rs fundamental frequencies of the plate

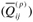
A limited number of papers concerning natural vibration of SMA fiber-reinforced composite plates can be found in the present literature. Zhong et al. (2006) proposed an experimental test procedure in order to measure fundamental natural frequency of smart plates. Two types of laminated composite plates with unidirectional and woven SMAs were fabricated and their vibration characteristics were investigated by both impact vibration tests and theoretical analysis. Stiffness and vibration characteristics of SMA/ER3 composites with shape memory alloy short fibers were experimentally investigated by Ni et al. (2007) experimentally. Lau (2002) investigated vibration characteristic of SMA composite beam in different boundary conditions using finite element method (FEM) and showed that increasing temperature in the composite beam with pre-strained SMA fibers caused increase of natural frequency and damping ratios of smart composite beams. Vibration of thermally post-buckled composite plates embedded with shape memory alloy fibers was studied by Park et al. (2004) using FEM and first shear deformation theory.

Numerical results representing critical temperature increased and thermal large deflection decreased using SMA fibers. Ostachowicz and Kaczmarczyk (2001) analyzed the dynamic response of composite laminated plate with a delamination defect subjected to aerodynamic loads using FEM. The results demonstrated that flutter boundaries can be modified using SMA fibers embedded in the plate. Ostachowicz et al. (1999) studied the influence of SMA fibers upon natural frequencies of the plate using FEM. The results of numerical calculations showed that SMA fibers can greatly influence natural frequencies of the plate. Ostachowicz et al. (2000) illustrated influence of SMA fibers upon changes in natural frequencies and thermal buckling of a composite multilayer plate with SMA components.

Birman et al. (1996) demonstrated that, if SMA wires were embedded in traditional polymer composites, tensile stresses could be generated inside the structures. Hence, impact resistance of the structures would be increased. He also demonstrated that, if some SMA wires were embedded in different layers of the structure, the global deflection of the structure would be reduced in low velocity impacts. Khalili et al. (2007) also studied effect of smart stiffening procedure on low-velocity impact response of smart structures.

In the present research, free vibration response of a rectangular smart hybrid composite plate was studied. The effect of some geometrical, physical and material parameters on the response of the composite plate embedded with SMA wires was also investigated. Some of the numerical results (which have not been reported in the literature so far) are presented in this paper.

2 CONSTITITIVE EQUATIONS

Constitutive equations of principal stress-strain relationship for a SMA hybrid laminated composite are as follows (Ostachowicz et al., 2000, Birman et al. 1996 and Khalili et al., 2007):

In the above equation, {σ} and {ε} represent stresses and strains in the principle directions, respectively. Q_ij and are reduced stiffness matrices for the SMA hybrid composite and composite medium (without the SMA wires), respectively. σr represents the recovery stress which can be determined analytically or experimentally (Birman et al. 1996 and Khalili et al., 2007). α^c_i (i = l , t) shows thermal expansion coefficients of the composite medium, calculated based on the temperature difference ΔT between the current and reference temperatures. Because of discontinuity function of stresses through the thickness between the layers, it is possible to determine constitutive equations considering the force-couple resultants in terms of stresses using integration of Equation (1) through the plate thickness, which yields:

whereN and S are vectors of forces and M is vector of moments, respectively. N ^r and M ^r are vectors of recovery stress resultants and the stress moments generated in the SMA wires, respectively. N ^T and M ^Tare vectors of the thermal stress resultants and the moments in the structure, respectively. Also, ε⁰ and γ are the mid-plane and shear strains and χ is the curvatures. In addition, ksh is the shear correction factor (Khalili et al., 2005, Whitney and Pagano, 1970 and Mindlin, 1951). In symmetrically laminated cross-ply plates:

Also, in Equation (2) (Khalili et al., 2007):

is the transformed reduced stiffness matrix of the p^th layer, defined as: where:

in which [T₁]_K and [T₂]_K are transformation matrices for the k^th layer and [Q^(p)_ij] is the reduced stiffness matrix of the lamina in the principal material coordinates, as given in Reddy (1997). In this paper, in all of the SMA embedded composite laminas, fibers of composite lamina and SMA wires can be in different. σ_r directions. is recovery stress and a function of temperature and pre-strain of the SMA wires.

Figure 1 (see Ostachowicz et al., 1999 and Ostachowicz et al., 2000) is used in a tabulated form in the computation and dynamic analyses. In Equation (5), α^c(p) and are coefficients of thermal expansion and volume fraction of composite medium in the pth ply, calculated in the following equations (Reddy, 1997 and Altenbach et al., 2004):

In plies with no SMA fibers, V_c^(k) = 1. In Equation (7), θ^(p) is the angle of fiber of the p^th lamina without embedded SMA wires.

3 GOVERNING EQUATIONS AND NAVIER'S SOLUTION

The plate equations developed by Whitney and Pagano (1970) were used since they included effect of transverse shear deformations (Figure 2). The assumed displacement field was:

Reducing the equation to a specially symmetric, cross ply orthotropic form (B_ij = 0, A₁₆ = A₂₆ = D₁₆ = D₂₆ = 0) and adding the uniform in-plane initial stress resultants and (see Equations (4-5)) resulted in (Mindlin, 1951and Reddy, 1997):

k_sh is the shear correction factor introduced by Mindlin (1951), normally taken to be π²/12. In addition, q is the dynamic normal load (transverse impact) over the plate and:

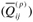(i, j = 1, 2, 6) are transformed reduced in-plane stiffness components and 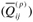(i, j = 1, 4, 5) are the transformed reduced transverse shear stiffness components, defined in Reddy (1997) and Altenbach et al. (2004).

In this work, attention was focused upon a simply supported rectangular plate with dimensions of a and b. Hence, the boundary conditions were as follows:

Figure 2 shows a SMA hybrid composite plate Khalili et al. (2007). The free vibration solution for a rectangular plate with simply supported boundary conditions at the upper and the lower face sheets was assumed to be of the following form:

The above double Fourier series of Dirichlet type functions can satisfy boundary conditions of the plate.In Equation (12), W_rs, A_rs and B_rs are unknown Fourier coefficients, r and s are half wave numbers in x and y directions, respectively, and ω is the vibration angular frequency. Hence, closed form solutions of the governing equations for free vibration of simply-supported rectangular composite plates with cross ply face sheets were obtained by applying Navier's technique. A 3x3 array of eigenvalue equations was also obtained. Since each coefficient of the Fourier series was independent, a one-term solution existed. Thus, the eigenvalue problem (Wilkinson, 1992) yielded only 3 eigen-frequencies for specified values of r and s. Then, Equation (9) could be reduced to the following eigenvalue equation:

where:

Equation (13) can be written as:

where:

The eigenvalue problem of Equation (15) is known as the standard eigenvalue problem (Khalili et al., 2005 and Reddy, 1997). By solving Equation (16), the eigenvalues can be analytically obtained (Khalili et al., 2007, Khalili et al., 2005 and Reddy, 1992):

Then, eigenvectors {X} can be analytically calculated using Equation (15). The shape modes of the plate can be calculated using Equation (12). In addition, using the following equations as discussed earlier (Khalili et al., 2005), values of strains (ε_x, ε_y, γ_xy, γ_xz and γ_yz) would be easily calculated:

In the above equations, z is thickness coordinate of the structure. Using Equation (6), stress-strain relations for any lamina in the laminated plate with respect to x, y and z axes are given by:

4 RESULTS AND DISCUSSION

In order to validate the present method and demonstrate its capability in predicting the free vibration response of composite plates with and without SMA wires, the results obtained from the present method were compared with those determined in Ostachowicz (1999) and Khalili et al. (2005).

4.1 Verifying of the Present Results

First, a ten-layered carbon/epoxy plate with size of 20cm×20cm and each layer's thickness of h = 0.269mm was analyzed. The material properties were as follows:

Stacking sequence of laminate was: [0 / θ 0 / –θ / 0]_s.The role of fibers' orientation of laminas in the plate was obtained considering a sequence 0 / θ / 0 / –θ ... of the fiber' orientations with respect to x axis.

First, the dynamic analysis was carried out to evaluate natural frequencies of vibrations of the plate without SMA wires, using the present method as well as the method in Khalili et al. (2005). The results are compared in Figure 3. It is observed that the maximum difference between the frequencies obtained by two methods was less than 2%. Because the effect of temperature on the composite medium and the SMA wires were considered in the present results, there was small discrepancy in the results. Second, the dynamic analysis was carried out to evaluate natural frequencies of vibrations of the plate embedded SMA wires, using the present method as well as the FEM in Ostachowicz (1999). Mechanical and physical properties of the shape memory alloys strongly depend on temperature and initial stresses (Ostachowicz, 1999).

Changes in temperature and initial stresses involve changes in the volume fraction of martensite in the alloys. During the martensite transformation, recovery stresses appear. These recovery stresses are not only a function of the temperature of the alloys but also depend on initial strains. In Figure 1, the SMA wires recovery stresses versus the temperature for four different initial strains are presented (Ostachowicz, 1999). It can be easily noticed that increase in the initial strains involved higher recovery stresses in the SMA wires and simultaneous changes in the temperatures of phase transformation were observed.

In this study, only a uniform temperature distribution in the plate was considered. The following material properties for the SMA wires were also used: austenite start temperature T_s = 37.8ºC and austenite finish temperature T_f = 62.8ºC. As an example, a simply supported square graphite-epoxy plate was investigated. The eight layer plate had the following orientation of graphite fibers [0/90/90/0]_S. Dimensions and material properties of the plate and SMA wires are given in Table 1.

The properties of graphite fibers are shown by index (f) and properties of epoxy matrix and SMA wires are shown by indices (m) and (s), respectively. The plate was modeled with 64 plate elements and the mesh size was 8 X 8 in (Ostachowicz, 1999). The volume fraction of graphite fibers in each layer was 0.2. In the present example, the SMA wires covered only 5% of the cross-sectional area of the plate. They were embedded in the neutral plane of the plate. It should be noticed that the relationship between the area and the internal forces was linear.

Certainly, the relationship between changes in natural frequencies and internal forces was not linear. In this paper, ω and are natural frequencies of plates with and without SMA wires, respectively. Also, NF = ω / is the dimensionless frequency parameter. All results of the presented numerical calculations were related to those obtained for the same plate without the SMA wires at room temperature of 20º C. Comparison of the present results of the variations of dimensionless natural frequency parameter ω / versus different temperatures of the SMA wires with results of Ostachowicz (1999) is shown in Table 2.

In addition, variation of the second and third dimensionless natural frequency parameters ω / versus different temperatures of the SMA wires obtained from the present method are presented in the table. The agreement between the results was quite good. The results of numerical investigations illustrated the influence of temperature of the SMA wires upon changes in bending natural frequencies of the plate. It can be clearly observed that the activation process of the SMA wires involved increase in the bending natural frequencies. This effect incaresed when both temperature and tensile pre-strains were higher.

The results obtained in this work demonstrated potential effectiveness of SMA fiber-reinforcement in composite structural elements in the control of vibrations. However, it must be noticed that the speed of response of changes in natural frequencies using the SMA wires was low. For this reason, SMA actuators can be used when high frequency controlling is not required. Nevertheless, internal forces generated in the SMA wires were much higher than those in other classes of smart materials, which allows for their application in these engineering applications.

Figures 4(a) and 4(b) show the first nine three dimensional transverse mode shapes and strains of the bottom layer of hybrid composite plate. The SMA temperature was constant and equal to austenite finish temperature T_f = 62.8ºC. These figures demonstrate that the lowest natural frequency was ω₁₁ = 669.32rad / sec.

4.2 Parametric Studies of the Free Vibration Problem

The effect of some of the geometrical, physical and material parameters on dynamic response of the hybrid composite plates was studied in this section. These parameters were some of the important factors affecting dynamic response and design of the smart structures. It was established that the dynamic behavior of the smart hybrid composite plate depended on various parameters such as volume fraction, temperature and tensile pre-strain of the SMA wires and the aspect ratio and fiber orientation of the laminated hybrid plate. Some of numerical results (which have not been reported in the literature thus far) were presented in this section. The used hybrid composite plate was symmetric. In all of the parametric studies, other than studying temperature effect, the SMA temperature was constant and equal to austenite finish temperature T_f = 62.8ºC.

The plate boundary conditions were simply supported. The plate consisted of eight layers of composite material with the angle of graphite fibers [0/90/90/0]_S. The dimensions and material properties of the plate and SMA wires are presented in Table 1. In order to study influence of stacking sequence of laminas, angle of plies of the composite plate was assumed to be [SMA(0) / θ / –θ / 0]_s and the effect of D₁₆ and D₂₆ was negligible. In all of parametric studies other than studying pre-strain effect, the initial strain was assumed ε_L = 4%.

4.2.1 Effect of SMA Temperature on Natural Frequencies

Effect of temperature of the SMA wires on dimensionless natural frequency parameter (NF) is shown in Figure 5. In this figure, relative changes in the first to the fifth bending natural frequencies are presented. The results of numerical investigations illustrated influence of the SMA fibers' temperature upon changes in bending natural frequencies of the analyzed plate. Figure 5 shows that effect of increasing SMA temperature on dimensionless fundamental NF was at the highest level.

The figure also shows that the variation of NF at temperatures between T_s < T < T_f (austenite transformation range) was larger than the variation of NF at other temperatures. It can be clearly observed that the activation process of the SMA wires involved increase in the bending natural frequencies. This effect increased when both temperature and initial strains were higher.

4.2.2 Effect of Tensile Pre-strain and Temperature of the SMA Wires on Free Vibration Response of Composite Hybrid Plate

Influence of tensile pre-strain of the SMA wires (at the final temperature of austenite transformation T = 62.8ºC) upon the relative changes of the first nine natural frequencies is shown in Figure 6. It can be clearly observed that the initial strain of SMA wires involved increase in the bending natural frequencies. Effect of both temperature and initial tensile pre-strain of the SMA wires on dimensionless natural frequency parameter (NF) is shown in Figure 7. This figure shows that the variation of NF at temperatures between T_s < T < T_f (austenite transformation range) was larger than the variation of NF at other temperatures. It can be clearly observed that the activation process of the SMA wires involved increase in the bending natural frequencies. This effect was intensified when both temperature and initial strains were higher.

As shown in Figure 7, with thermal expanding of the composite graphite epoxy plate and the austenite phase of SMA wires (αΔT), the fundamental frequency of the plate considerably decreased as the SMA temperature increased (for ε_L = 1% to ε_L < 3% and T > T_f). This reduction of the fundamental frequency could be considerably compensated for by increasing tensile pre-strain of the SMA wires (ε_L > 3%).

4.2.3 Effect of Tensile Pre-strain of the SMA Wires and the Plate Aspect Ratio on Fundamental Natural Frequency of the Plate

Figure 8 shows that fundamental natural frequency increased with the increased aspect ratio a/b. Because, as aspect ratio (a/b) increased, length of plate increased and the plate was closer to a beam. However, boundary conditions were applicable on all four edges, which resulted in the decrease of vertical and shear deformations and increase of stiffness of the plate as well as coupling effects between the membrane, bending and shear terms. Therefore, the bending stiffness and fundamental natural frequency increased with the increased aspect ratio a/b.

Effect of both aspect ratio of the composite plate and tensile pre-strain of the SMA wires on the first natural frequency is shown in Figure 8. It can be clearly observed that the activation process of the SMA wires involved increase in the bending natural frequencies only for a/b<2.4. The SMA wires were embedded along the x axis (along length of the plate). As the volume fraction of SMA wires decreased with the increase of the plate's aspect ratio a/b, the effect of tensile pre-strain and activation process of the SMA wires on increase of the first natural frequency was slight and negligible, especially for a/b>2.4. Since the increase of the aspect ratio represented decreased wire volume fraction in the composite plates, therefore, the recovery force acted into the plate became insignificant.

4.2.4 Effect of Volume Fraction and Temperature of SMA Wires on Fundamental Natural Frequency of the Plate

Effect of temperature and volume fraction of SMA wires on fundamental natural frequency is illustrated in Figure 9. The results of numerical investigations illustrated the influence of the SMA volume fraction upon changes in bending natural frequencies of the analyzed plate. The figure shows that the variation of fundamental natural frequency at temperatures between T_s < T < T_f (austenite transformation range) was larger than the variation of fundamental natural frequency at other temperatures. The volume fractions of the SMA wires were considered 0.005 to 0.095. The wires were placed only along the x direction. It is evident in Figure 9 that, by increasing volume fraction of the SMA wires, the fundamental natural frequency increased. As shown in the figure, with thermal expansion of composite graphite epoxy plate and austenite phase of the SMA wires (αΔT), the fundamental frequency of the plate decreased considerably as the SMA temperature increased (for V_s = 0.005 to V_s = 0.035 and T > T_f). This reduction of the fundamental frequency could be considerably compensated for by increasing volume fraction of the SMA wires (V_s = 0.035).

5 CONCLUSIONS

In this research, free vibration response of smart hybrid composite structures was studied using the simultaneous application of FSDT and Fourier series to analytically solve system of the governing differential equations of the plate. The results of the present research demonstrated that:

1) Using of the SMA wires inside the hybrid composite plates changed natural frequencies as well as global behavior of the structure.

2) Some of the geometrical, physical and material parameters like volume fraction and tensile pre-strain of the SMA wires and the plate's aspect ratio were important factors affecting free vibrations response and design of the structures.

3) The variation of dimensionless natural frequency parameter (NF) at temperatures between T_s < T < T_f (austenite transformation range) was larger than the variation of NF at other temperatures.

4) Activation process of the SMA wires involved increase in the bending natural frequencies. This effect was intensified when both temperature and initial strains were higher.

5) Tensile pre-strain of the SMA wires involved increase in the bending natural frequencies.

6) The bending stiffness and fundamental natural frequency increased with the increase in the plate's aspect ratio a/b.

7) Activation process of the SMA wires involved increase in the bending natural frequencies only for a/b<2.4.

8) As the volume fraction of SMA wires decreased with the increase of the plate's aspect ratio a/b, effect of tensile pre-strain and activation process of the SMA wires on increase of the first natural frequency was slight and ignorable, especially for a/b>2.4.

9) By increasing volume fraction of the SMA wires, the fundamental natural frequency increased.

10) With thermal expansion of the composite graphite epoxy plate and the austenite phase of SMA wires (αΔT), the fundamental frequency of the plate decreased considerably as the SMA temperature increased (For V_s = 0.005 to V_s = 0.035 and T > T_f). This reduction of the fundamental frequency could be considerably compensated for by increasing volume fraction of the SMA wires (V_s = 0.035).

Received in 28 Feb 2013

In revised form 10 Jun 2013

• Altenbach, H., Altenbach, J. and Kissing, W., (2004). Mechanics of composite structural elements, Springer, 122-297.
• Birman, V., Chandrashekhara, K. and Sain., S., (1996). An Approach to Optimization of Shape Memory Alloy Hybrid Composite Plates Subjected to Low-velocity Impact, Composites: Part B, 27B: 439-446.
• Khalili, M. R., Malekzadeh, K. and Mittal, R. K., (2005). A new approach to static and dynamic analysis of composite plates with different boundary conditions, Composite Structures, 69: 149-155.
• Khalili , S. M. R., Shokuhfar, A. and AshenaiGhasemi, F., (2007). Effect of smart stiffening procedure on low-velocity impact response of smart structures, Journal of Materials Processing Technology, 190: 142152.
• Lau, K. T. (2002). Vibration characteristics of SMA composite beams with different boundary conditions, Materials and Design. 23: 741749.
• Mindlin, R. D. (1951). Influence of rotary inertia and shear on flexural motions of isotropic elastic plates, J. of Appl. Mech., 18: 31-38.
• Ni, Qing-Q., Zhang, Run-xin., Natsuki, T. and Iwamoto, M., (2007). Stiffness and vibration characteristics of SMA/ER3 composites with shape memory alloy short fibers, Composite Structures, 79: 501507.
• Ostachowicz, W. M., Krawczuk, A. Zak., (1999). Natural frequencies of a multilayer composite plate with shape memory alloy wires, Finite Elements in Analysis and Design, 32: 71-83.
• Ostachowicz, W. M., Krawczuk, A. Zak., (2000). Dynamics and buckling of a multilayer composite plate with embedded SMA wires, Composite Structures, 48: 163-167.
• Ostachowicz, W. M., Kaczmarczyk, S., (2001). Vibration of composite plate with SMA fibers in a gas stream with defect of the type of delamination, Composite Structures, 54: 305311.
• Park, J. S., Kim, J. H., Moon, S. H., (2004). Vibration of thermally post-buckled composite plates embedded with shape memory alloy fibers, Composite Structures, 63: 179188.
• Reddy, J. N. (1997). Introduction to composite materials, Mechanics of laminated composite plates and shells, Second Edition, 88, CRC Press, United States of America.
• Whitney, J. M. and Pagano N. J., (1970). Shear deformation in heterogeneous anisotropis plates, J. Appl. Mech., 37: 1031-1036.
• Wilkinson, J. H. (1992). The algebraic eigenvalue problem, Clarendon Press. Oxford. in : S.S. Rao., Mechanical Vibrations. Pergamon Press. Oxford, 285-300.
• Zhang, Run-xin, Ni, Qing-Q., Masuda, A., Yamamura, T. and Iwamoto, M., (2006). Vibration characteristics of Laminated Composite Plates with embedded Shape memory alloys, Composite Structures, 74(4): 389-398.

Publication Dates

• Publication in this collection
  30 July 2013
• Date of issue
  Mar 2014

History

• Received
  28 Feb 2013
• Accepted
  10 June 2013