Abstract
The thermal entry region in laminar forced convection of Herschel-Bulkley fluids is solved analytically through the integral transform technique, for both circular and parallel-plates ducts, which are maintained at a prescribed wall temperature or at a prescribed wall heat flux. The local Nusselt numbers are obtained with high accuracy in both developing and fully-developed thermal regions, and critical comparisons with previously reported numerical results are performed.
Integral transform technique; internal forced convection; Herschel-Bulkley fluids
INTEGRAL TRANSFORM SOLUTION FOR THE FORCED CONVECTION OF HERSCHEL-BULKLEY FLUIDS IN CIRCULAR TUBES AND PARALLEL-PLATES DUCTS
J. N. N. QUARESMA1 and E. N. MACÊDO2
1Chemical Engineering Department - CT - Universidade Federal do Pará - UFPA, Campus Universitário do Guamá, Rua Augusto Corrêa, 01 - 66075-900, Belém, PA, Brazil.
e-mail: quaresma@marajo.ufpa.br
2Mechanical Engineering Department - CT - Universidade Federal do Pará - UFPA, Campus Universitário do Guamá, Rua Augusto Corrêa, 01 - 66075-900, Belém, PA, Brazil
(Received: July 6, 1997; Accepted: February 17, 1998)
Abstract - The thermal entry region in laminar forced convection of Herschel-Bulkley fluids is solved analytically through the integral transform technique, for both circular and parallel-plates ducts, which are maintained at a prescribed wall temperature or at a prescribed wall heat flux. The local Nusselt numbers are obtained with high accuracy in both developing and fully-developed thermal regions, and critical comparisons with previously reported numerical results are performed.
Keywords: Integral transform technique, internal forced convection, Herschel-Bulkley fluids.
INTRODUCTION
The analysis of convection heat transfer to non-newtonian fluids inside ducts is of great importance in the design of thermal equipment in the pharmaceutical, food and petrochemical industries. This non-newtonian behavior is encountered in materials such as: solutions or melts of polymeric materials, oils and greases, cosmetics, toothpaste, soap and detergents, paints, cement and drilling muds. During the drilling operation, particularly in the petroleum industry, certain drilling muds and cements are of fundamental importance in providing a good operation and the well cementing. These drilling muds follow a non-newtonian behavior based on the Herschel-Bulkley model, a power-law fluid model with yield-stress, and their rheological properties are sensitive to the temperature. Therefore, the determination of the temperature distributions in such fluids are necessary for the complete control of these properties during the drilling operation.
Thus, in this context, the present work deals with the thermal problem in both the entry and fully-developed regions of fluids that follow the Herschel-Bulkley model, inside circular and parallel-plates ducts. The solution of this problem is obtained by applying the integral transform technique.
The analytic solution in the thermal entry region for both laminar and turbulent forced convection inside ducts involves difficulties due to the related auxiliary eigenvalue problem (Özisik et al., 1989). Previous works have employed purely numerical techniques to solve the eigenvalue problem (Sellars et al., 1956; Shibani and Özisik, 1977), such as the Runge-Kutta method, but only the first few eigenvalues can be determined by this technique. Consequently, it is not feasible to calculate heat transfer results in regions which are very close to the duct inlet because a large number of eigenvalues are needed for the computation of the series expansion based on the eigenfunctions.
In the 80s, Mikhailov and Vulchanov (1983) and Mikhailov and Özisik (1984) advanced the so-called Sign-Count Method based on the approaches of Wittrick and Williams (1971, 1974), in order to solve the related Sturm-Liouville type eigenvalue problem, which permits the automatic and .highly accurately .determination .of .as .many eigenvalues .and .eigenfunctions .as are needed.
More recently, Cotta (1993) and Mikhailov and Cotta (1994), also developed an approach to solve eigenvalue problems based on the ideas of Generalized Integral Transform Technique (GITT) which was demonstrated to be as efficient and safe as the sign-count method.
Therefore, to alleviate such difficulties pointed out in the solution of this heat transfer problem, and to be able to perform heat transfer calculations in regions very close to the duct inlet with a high degree of accuracy, the ideas on Integral Transform Technique in conjunction with the well-established sign-count method and GITT are used in the present work, aimed at establishing benchmark results for this problem.
ANALYSIS
(1.a)
(1.b)
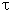
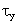
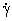
For the fully-developed region of a circular or a parallel-plates duct, the momentum equation in the axial coordinate z, is simplified to yield:
, (2.a)
in 0 < r < b, z > 0
subjected to the following boundary conditions
(2.b)
(2.c)
where the exponent p denotes the channel geometry and is written as:
(3.a, b)
Then, introducing equations (1) in equation (2.a), noting that 
and after the integrations are performed, the fully-developed velocity profile for Herschel-Bulkley fluids is given by:
(4.a)
and,
(4.b)
where bo represents the radius of the plug-flow region defined as:
(5)
The velocity profile given by equations (4) for a Herschel-Bulkley fluid is split in two distinct regions, one for 
which denotes the plug-flow region where 
, and the fluid behaves like a solid plug, and another region for 
where 
, and refers to that part of the fluid which is in shear flow (Forrest and Wilkinson, 1973).
In the analysis of the thermal problem, we consider steady-state laminar forced convection heat transfer to hydrodynamically developed flow in the thermal entry region of an incompressible non-newtonian fluid that follows the Herschel-Bulkley model, described by equations (1) and (4), inside both circular and parallel-plates ducts maintained at a prescribed wall temperature Tw, or at a prescribed wall heat flux qw. The fluid enters the channels with a constant uniform temperature To.
Axial heat conduction and viscous dissipation are neglected and the physical properties are considered temperature independent.
Then, the mathematical formulation of this heat transfer problem in dimensionless form is defined by:
(6.a)
subjected to the boundary and inlet conditions:
;
(6.b, c)
(6.d)
where in the boundary conditions (6.c), the coefficient m identifies whether the duct wall is subjected to a prescribed temperature or to a prescribed heat flux, in the following form:
(7.a, b)
In equations (6) above the following dimensionless groups were used:
(8.a-g)
where Dh is the hydraulic diameter, defined as:
(9)
The velocity profile given by equations (4) is written in dimensionless form by introducing the groups (8), or:
(10.a)
and,
(10.b)
where the additional groups employed in the above equations are Ro (the dimensionless radius of the plug-flow region), Y (the yield number) and f (the Fanning friction factor), i. e.,
(11.a-c)
The Fanning friction factor and the dimensionless radius of the plug-flow region are functions of the Reynolds and yield numbers. The determination of both quantities is obtained by resolution of a simple transcendental equation, and due to space limitations is not described here. Table 1 below shows some results for the product f Re.
The problem given by equations (6) can be solved by the classical integral transform technique (Mikhailov and Özisik, 1984; Cotta, 1993). In order to make the boundary conditions (6.c) homogeneous, so as to obtain a better computational performance in the series expansion, a splitting-up procedure is proposed as (Mikhailov, 1977; Mikhailov and Özisik, 1984):
(12)
is the average temperature, defined as:
(13)
and, for the case of a prescribed wall heat flux, when we have all boundary conditions of the second kind, the average temperature is given a priori in the form:
(14)
Now, introducing equation (12) into equations (6), the following problems for the potentials 
and 
are obtained:
(15.a)
(15.b, c)
with its respective solution:
(16)
and,
(17.a)
with initial and boundary conditions:
(17.b)
(17.c, d)
The homogeneous problem defined above by equations (17) can also be solved by the classical integral transform technique. Then, following the procedures of this technique, the appropriate eigenvalue problem needed for its solution is given by:
(18.a)
(18.b,c)
where 
and 
are, respectively, the eigenfunctions and eigenvalues. The eigenvalue problem allows for the development of the
following integral transform pair:
, (19.a,b)
where the normalization integral is given by:
(20)
Then, taking the integral transform of the system given by equation (17), these equations are operated with 
, and we obtain the following ordinary differential equation for the transformed potential, 
:
(21.a)
with the transformed inlet condition given by:
(21.b)
The solution for the transformed potential given by equations (21) is readily obtained in the form:
(22)
Therefore, introducing equation (22) into the inversion formula (19.a), the solution for is determined as:
(23)
Thus, equation(23) in conjunction with equation (16) for complete the solution for the potential 
defined in equation (12). For the case of a prescribed wall heat flux, the average temperature is given by equation (14). For the case
of a prescribed wall temperature, when it isnt determined a priori, it may be readily obtained by substituting the solution for , equation (12), with m = 0, into equation (13) to yield:
(24)
The local Nusselt number for both situations is defined as:
(25)
after substituting equation (12) for 
, and equation (24), for the case of a prescribed wall temperature, into equation (25) above, the two distinct situations result:
, (26)
for m = 0
the asymptotic Nusselt number, 
,for this case, is obtained from equation (26), by considering only the first term in the summation, to yield:
(27)
while,
, (28)
for m = 1
where, 
is obtained from equation (16) in the form
(29)
and in this case the asymptotic Nusselt number, , is given by equation (28), making 
, so that
(30)
To complete the solution it is necessary to evaluate the eigenvalues, , the eigenfunctions 
and the normalization integral 
of the eigenvalue problem (18). Here, for instance, we have used both the sign-count method established in references (Mikhailov and Vulchanov, 1983; Mikhailov and Özisik, 1984) and the generalized integral transform technique (Cotta, 1993; Mikhailov and Cotta, 1994) to determine the eigenvalues and other related eigenquantities necessary to compute the average temperature and the local Nusselt numbers from equations (24) and (26-30).
RESULTS AND DISCUSSION
First, the eigenvalues and other related eigenquantities were obtained by the two approaches cited above. The results obtained through the two approaches are in perfect agreement. Due to space limitations they are not listed here. Then, the average temperature, 
, and the local Nusselt numbers, 
, were calculated.
In Tables 2.a to 2.d, the present results are validated against previous results for power-law fluids presented by Cotta and Özisik (1986a, 1986b), in the thermal entry region, for the case of Y = 0 and n = 1/3, 1 and 3. From these tables it can be noticed that the results are in excellent agreement, providing a direct validation of the numerical code developed in this work.
Table 3.a shows the asymptotic Nusselt number from the present analysis and its comparison with those computed by Lin and Shah (1978) for various power-law exponents and yield numbers for both circular tubes and parallel-plates channels and considering a prescribed wall temperature. A similar analysis is also shown in Table 3.b for the case of a prescribed wall heat flux. An excellent agreement between the results can be observed from these tables.
* - Cotta and Ozisik (1986a)
(prescribed wall temperature)
+ - Present work
* - Cotta and Özisik (1986b)
+ - Present work
*- Lin and Shah (1978)
+ - Present work
* - Lin and Shah (1978)
For the case of prescribed wall heat flux in a circular duct, Figure 1 shows the evolution of the local Nusselt number as a function of the axial coordinate, Z, in the thermal entry region. The power-law exponent here considered was n = 1 (newtonian situation) and the yield numbers were Y = 0, 5, 10 and 20. The analysis permits the comparison among the results from the present work and those obtained by Lin and Shah (1978) over the range 5x10-3
1, and those by Nouar et al. (1994) over the range of 5x10-6 10-1. From this figure only a reasonable agreement is observed between the results obtained by the two analyses, with a better agreement for increasing axial coordinate Z, i.e., only in the vicinity of the fully-developed region. Therefore, the two previous works, that have employed finite-differences schemes could not obtain numerical results with high accuracy in the thermal entry region.
In Figures 2 and 3 the local Nusselt numbers are shown in the thermal entry region for the case of prescribed wall temperature for both adopted geometries and for various power-law exponents and yield numbers. The increase of the power-law exponent shows a Nusselt number decrease, while for an increasing yield number there is an increase in the Nusselt number. These results are systematically larger for parallel-plates channels than for circular tubes.
Figures 4 and 5 present a similar analysis for the case of a prescribed wall heat flux and the same observations are noted in relation to the parameters studied, i.e., power-law exponents, yield numbers and geometries of the channels. Finally, from these figures it is also observed that the Nusselt numbers for the case of a prescribed wall heat flux are larger than those for the case of a prescribed wall temperature.
Figure 1: Comparison of the Nusselt number in the thermal entry region for prescribed wall heat flux in a circular tube.
- Local Nusselt number in the thermal entry region for prescribed wall temperature in a parallel-plates channel; (a) n = 0.5; (b) n = 1.5
- Local Nusselt number in the thermal entry region for prescribed wall temperature in a circular tube; (a) n = 0.5; (b) n = 1.5
- Local Nusselt number in the thermal entry region for prescribed wall heat flux in a parallel-plates channel; (a) n = 0.5; (b) n = 1.5
- Local Nusselt number in the thermal entry region for prescribed wall heat flux in a circular tube; (a) n = 0.5; (b) n = 1.5
CONCLUSIONS
The problem of laminar convective heat transfer in the thermal entry and fully-developed flow regions of a Herschel-Bulkley fluid, for both prescribed wall temperature and prescribed wall heat flux, and for circular and parallel-plates channel, has been analyzed, with excellent computational performance, through the Integral Transform Technique in conjunction with the Sign-Count method and Generalized Integral Transform Technique (GITT) approaches for the solution of the related eigenvalue problem.
Benchmark results are then tabulated and graphically presented for various power-law exponents and yield numbers.
NOMENCLATURE
b Radius of circular duct or one half the spacing between parallel-plates, m
bo Radius of plug-flow region, m
Dh Hydraulic diameter, m
f Fanning friction factor
h (z) Local heat transfer coefficient, W/m2.K
k Thermal conductivity, W/m.K
K Consistency index of the fluid, N.sn/m2
m Coefficient defined in equations (7)
n Power-law exponent
Ni Normalization integral
Nu (Z) Local Nusselt number
Asymptotic Nusselt number
p Parameter of channel geometry or pressure
Pr Prandtl number
qw Prescribed wall heat flux, W/m2
r, R Radial coordinate, dimensional and dimensionless
Re Reynolds number
Ro Dimensionless radius of plug-flow region
To Inlet temperature (K)
Tw Prescribed wall temperature, K
um Average flow velocity, m/s
u(r), U(R) Velocity distribution, dimensional and dimensionless
W (R) Defined by equations (8)
Y Yield number
z, Z Axial coordinate, dimensional and dimensionless
Greek Symbols
a Fluid thermal diffusivity, m2/s
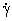Shear rate, s-1
Eigenvalues of problem (18)
Eigenfunctions of problem (18)
Density, Kg/m3
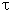Shear stress, N/m2
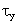Yield stress, N/m2
Dimensionless temperature distribution
Dimensionless average temperature
- Cotta, R. M., Integral Transforms in Computational Heat and Fluid Flow, CRC Press, Boca Raton (1993).
- Cotta, R. M. and Özisik, M. N., Laminar Forced Convection to Non-Newtonian Fluids in Ducts with Prescribed Wall Heat Flux, Int. Comm. Heat Mass Transfer, 13, 325-334 (1986a).
- Cotta, R. M. and Özisik, M. N., Laminar Forced Convection of Power-Law Non-Newtonian Fluids Inside Ducts, Wärme-und Stoffübertragung, 20, 211-218 (1986b).
- Forrest, G. and Wilkinson, W. L., Laminar Heat Transfer to Temperature-Dependent Bingham Fluids in Tubes, Int. J. Heat Mass Transfer, 16, 2377-2391 (1973).
- Lin, T. and Shah, V. L., Numerical Solution of Heat Transfer to Yield Power Law Fluids Flowing in the Entrance Region, Proc. of the 6th International Heat Transfer Conference, 5, 317-322, Toronto (1978).
- Mendes, P. R. S. and Naccache, M. F., Heat Transfer to Herschel-Bulkley Fluids in Laminar Fully Developed Flow through Tubes, Proc. of the 13th Brazilian Congress of Mechanical Engineering, XIII COBEM, Belo Horizonte, Brazil, December (1995).
- Mikhailov, M. D., Splitting Up of Heat-Conduction Problems, Letters Heat Mass Transf., 4, 163-166 (1977).
- Mikhailov, M. D. and Cotta, R. M.., Integral Transform Method for Eigenvalue Problems, Comm. Num. Meth. Eng., 10, 827-835 (1994).
- Mikhailov, M. D. and Özisik, M. N., Unified Analysis and Solutions of Heat and Mass Diffusion, John Wiley, New York (1984).
- Mikhailov, M. D. and Vulchanov, N. L., Computational Procedure for Sturm-Liouville Problems, J. Comp. Phys., 50, 323-336 (1983).
- Nouar, C.; Devienne, R. and Lebouche, M., Convection Thermique pour un Fluide de Herschel-Bulkley dans la Région dEntrée dune Conduite, Int. J. Heat Mass Transfer, 37, 1-12 (1994).
- Özisik, M. N.; Cotta, R. M. and Kim, W. S., Heat Transfer in Turbulent Forced Convection Between Parallel-Plates, Can. J. Chem. Eng., 67, 771-776 (1989).
- Sellars, J. R.; Tribus, M. and Klein, J. S., Heat Transfer to Laminar Flow in a Round Tube or a Flat Conduit - The Graetz Problem Extended, Trans. Am. Soc. Mech. Eng., 78, 441-448 (1956).
- Shibani, A. S. and Özisik, M. N., A Solution to Heat Transfer in Turbulent Flow Between Parallel Plates, Int. J. Heat Mass Transfer, 20, 565-573 (1977).
- Wittrick, W. H. and Williams, F. W., A General Algorithm for Computing Natural Frequencies of Elastic Structures, Quart. J. Mech. Appl. Math., 24, 263-284 (1971).
- Wittrick, W. H. and Williams, F. W., Buckling and Vibrations of Anisotropic or Isotropic Plate Assemblies under Combined Loading, Int. J. Mech. Sci. , 16, 209-239 (1974).
Publication Dates
-
Publication in this collection
09 Oct 1998 -
Date of issue
Mar 1998
History
-
Accepted
17 Feb 1998 -
Received
06 July 1997
