Small amplitude oscillations of sine-gordon vortex states in planar magnets in three dimensions

a25v32n3

Small Amplitude Oscillations of Sine-Gordon Vortex States in Planar Magnets in Three Dimensions

A . R. Pereira

Departamento de Física, Universidade Federal de Viçosa,

Viçosa, 36571-000, MG, Brazil

Received on 10 June, 2002

We investigate the spectrum of small amplitude oscillations of the sine-Gordon vortex-antivortex pair in layered ferromagnetic systems described by the anisotropic three-dimensional XY-model. In the case of a small interlayer coupling constant, vortex-pairs can be formed independently in each plane. Analytical expressions for two discrete modes with zero frequency are obtained. These zero modes are associated with the two-dimensional motion of the excitation on an individual plane and are important because the interference between them and a vortex-pair gives rise to contributions to the central peak. The continuum states, which contribute to EPR linewidth, are derived using the Born approximation.

As it is well known, two-dimensional magnetic systems having a XY-like continuous symmetry at finite temperature and for zero magnetic field exhibit a topological long-range order and a phase transition involving the unbinding of vortex-pairs at a critical temperature T_KT, the Kosterlitz-Thouless temperature [1]. However, effects of relevant perturbations, such as a magnetic field applied along the plane or the presence of an inter-plane coupling J_z , change this picture dramatically. For the three-dimensional XY-model with a layered structure, even for a very small coupling between the planes, the system will show the conventional long-range order at low temperatures and an usual second-order transition at a temperature T_c which is higher than T_KT of the isolated layer. The vortex-antivortex interaction does not grow logarithmically with the distance between the vortex centers as in the ideal two-dimensional model, but becomes linear for large distances of separation [2,3]. The same happens to the two-dimensional XY-model in the presence of a magnetic field applied along the plane [4,5]. In fact, it has been shown that this two-dimensional XY-model with an in-plane magnetic field can be viewed as a mean-field theory of the anisotropic three-dimensional XY-model with a very weak coupling between the planes [4]. This is because the correlations of the fluctuations between the layers are small owing to the smallness of the interlayer coupling.

The linear large distance dependence for the vortex-antivortex interaction, E_v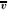µ E₂R, where R is the distance between the vortex centers, indicates that there are no free vortices in the XY-model in the presence of an external magnetic field applied along one of the in-plane axis. However, in the three-dimensional case, Minnhagen and Olsson [3] have suggested that the effective interplane coupling E₂(T), at a critical temperature T_c, renormalizes to zero, leading to the correspondence of a Kosterlitz-Thouless transition. This critical temperature has been determined in recent Monte Carlo calculations and its value, for very small interlayer couplings (J_z

J, where J is the intra-plane coupling between spins S), is estimated in the range 0.725JS² < T_c £ 0.90JS² [6] depending on the values of the anisotropy (0 < J_z/J < 0.1), while for the isotropic three-dimensional XY-model (J_z = J), it was estimated as T_c = 1.54JS² in Refs.[6,7] and T_c = 1.5518JS² in Ref. [8]. Our worry is with the case J_z

J, in which vortex-pairs can be formed independently in each layer and E₂ can be renormalized. This renormalization is due to spin waves and vortices in the plane that the vortex-antivortex pair belongs to, as well as to spin waves and vortices in the surrounding planes [3,6,9]. While the static properties of these systems were studied in some detail, the dynamical behavior is not well developed. One point of fundamental importance to study in the dynamics of this three-dimensional model, and which may also be related to the mechanism of renormalization of the inter-plane coupling, is the interaction between spin waves and topological excitations in the plane that the topological excitation belongs to. These interactions can lead to relevant information about the properties of the system and can also be used in the perturbations theories involving non-linear excitations response to external perturbations or forces, quantization procedures for soliton states, as well as in statistical mechanics [10]. The presence of a topological excitation in the system provides a localized potential seen by linear solutions (magnons) in the sense that small deviations from the static topological structure must satisfy a Schrödinger-like equation in which the potential well is due to the presence of the topological excitation. Recently, local modes and scattering states of vortices were calculated [11,12] for pure two-dimensional magnetic materials and used to propose possible experimental confirmations of solitons [13] and vortices [14]. Since the vortex-pairs are essential to understand the XY-models with perturbations, then, in this paper we consider the vortex-pair interacting with magnons in the three-dimensional XY ferromagnetic model with weak coupling between the planes. We start defining the Hamiltonian of the three-dimensional classical ferromagnetic model with predominant interaction J in the plane of the layer and weak interaction J_z between layers (J_z

J)

where the index n numbers different planes of the layer and the sum i,j is only over nearest neighbors of the lattice sites in the planes. The classical spin vector localized at layer n and site i, _n,i = can be parametrized by two scalar fields q_n,i, f_n,i and written as _,i = S(cosq_n,icosf_n,i,cosq_n,isinf_n,i, sinq_n,i). At low temperatures T T_c, we can adopt a mean field approximation for the interlayer coupling assuming that ád_n·d_n+1ñ áñ² and then, Hamiltonian (1) can be approximated by [4]

In Eq.(2) we define a reduced magnetic field (mean field) 2J_z|áñ| with direction parallel to the x-axis in the spin space. Using the continuum approximation to Hamiltonian (2) on each layer

where we have taken S = 1 and a₀ is the lattice spacing, we get the followings equations of motion

Static in-plane solutions of these equations are those which solve the two-dimensional sine-Gordon equation

and then, below T_c this system reveals a quite interesting behavior, which is due to the vortex-antivortex pair formations in the plane of the layer, since the sine-Gordon equation possess vortex solutions. In fact, Hikami and Tsuneto [15] first showed that the vortex pairs can also be formed in the layered system of XY-model and then they proved that, in certain circumstances, it is energetically favorable for the vortex pairs in different layers to become independent instead of making a vortex ring. An exact vortex solution for equation (6) was obtained by Hudák [16], but we cannot be sure that this solution can be applied directly to the discrete lattice, since the vortex and antivortex vorticities in a pair are 4 and -4 respectively. Cataudella and Minnhagen [2] have shown that, in the study of vortex excitations, when we are interested in the analytical description of topological excitations, it is more convenient to consider that, for weak couplings, the coupling between adjacent layers leads to small deviations, at low temperatures, from the vortex-pair solution for the ideal planar ferromagnet. It is equivalent to approximate sin f f in the sine-Gordon equation and the vortex-antivortex solution obtained from this approximation is given by

where K₀ is the modified Bessel function and the vortex is located at (0,a) and the antivortex at (0,-a). The energy of this excitation is [2,3]

where R = 2a, E₀ is the creation energy of a vortex pair, E₁ = 2pJ and E₂ = p². The coefficient of the linear term in the energy decreases as the temperature increases, vanishing at T = T_c and here, it is indicated by the mean magnetization áñ present in E₂ [6]. The contribution of the structures (7) to the dynamical correlation functions in these layered classical ferromagnet was studied by Pires et al. [17].

The object now is to study what effect such topological structures have on the associated long wavelength ferromagnetic spin waves propagating on the layer n. To this end, we assume that the deviations from the static configuration (7) due to the presence of spin waves, are small with harmonic time dependence

with q_v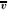(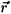) = 0 for a planar pair and a ,b 1. Substituting Eqs. (9) into the equations of motion and linearizing in the small quantities, we obtain for the in-plane spin wave oscillations, a Schrödinger-like differential equation with zero eigenvalue

and with a frequency dependent potential not cylindrically symmetric given by

The out of plane spin wave oscillations are obtained from the in-plane oscillations through

In the mean field approximation, the essential effect of the adjacent planes on the spin wave propagation on a layer is to introduce a finite activation dispersion law given by 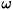2 = 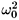+ ^k2, due to the mean magnetization áñ where 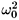= J_z J | áñ | (4/-J_z | áñ |/J), = J² (4/-J_z | áñ |/ J ) and k² = + is the wave vector modulus. The lowest-order effect of an inhomogeneous vortex-pair background is to produce an elastic scattering center for the spin waves, since the potential (11) has a finite range of the order of the size of the pair configuration R. Thus, in polar coordinates (r,j), asymptotic solutions to Eq. (10) for the continuum states (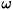²³ 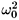), are given by phase-shifted cylindrical spin waves

where D_{n n¢} is the phase-shift matrix coupling the different angular momentum channels n and n¢ and , denotes the Hanckel functions. Since the potential V(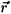, 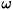) is no longer cylindrically symmetric, the angular momentum is no longer a good quantum number, nor is the phase-shift matrix D_{n n¢} any longer diagonal. There are transitions between the various angular momentum channels due to the coupling between the angular dependence of the spin wave and the angular dependence of the scattering potential.

Besides the continuum states with

²³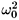 , equation (10) has two discrete levels with zero-frequency. The zero modes are associated with the fact that the spectrum of small oscillations must contain zero-mode translation modes to restore the translation invariance broken by the presence of a pair into the system. The wave functions of these translation modes, which we denote by b₀₁(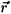) and b₀₂(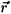), are proportional to the partial derivatives ¶f_v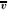/ ¶x and ¶f_v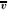/ ¶y respectively, and hence, the zero mode with 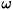= 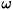₀₁ =0 is associated with a translation along the x-direction and analogously, the zero mode with 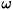= 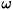02 = 0 is associated with the translation along the y-direction. They are given by a₀₁(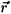) = a₀₂(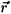) = 0 and

These local modes govern the motion of the pair on the layer n and are of fundamental importance in the study of dynamics of topological excitations in the presence of external perturbations. Local modes, specially zero modes, are of paramount importance in the derivation of a topological excitation thermodynamics [10,18]. In fact, the number of magnons states must be decreased by a number equal to the number of bound states. One way to view this decrease is that topological excitation traps magnon states due to its presence and thus, the degrees of freedom (or free energy, etc) are shared between modes of a non-linear system. Besides, the local modes may be related to the resonance phenomena in vortex-antivortex collisions because the pair internal interaction due to E_n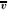µ E₂R may have energy exchange with the pair translational modes during the collisions.

The continuum states with frequencies 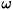³ 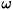₀ can be found using the Born approximation. Based on the asymptotic behavior of the scattering equation, we can rewrite Eq. (10) as Ѳb+k²b = U(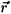, 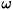)b, where U(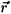, 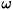) = V(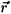,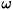)+k². The Green function associated to the Helmholtz operator Ѳ+k² in two dimensions is (i/4)H₀⁽¹⁾(k|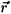- |) and hence, the formal solution of Eq.(10) is

Using the Born approximation we can take b() b⁽⁰⁾() = e for the first order Born term and so on. In general this integral can only be calculated numerically, but equations (10) and (12) can be written as

and then, we can approximate the spatial dependence of the oscillations substituting b⁽⁰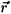⁾() into Eq.(18) to find a⁽¹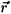⁾() and substituting a⁽¹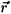⁾() into Eq.(17) to find b⁽¹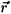⁾() and so on. Assuming that the potential is small, we neglect terms of order higher than 2 in the potential to obtain

The out-of-plane oscillations can be written from Eq.(19) using the relation (12). Of course, as we should expect, the scattered states as well as the local modes are not radially symmetric.

As it was discussed in Ref. [13], these scattering states provide an indirect method to experimentally detect topological excitations, through EPR linewidth measurements. The linewidth is the temporal integral of the four-spin correlation function and the structure factor used to calculate them contains a static contribution from the static pair solution and a time-dependent contribution from pair-magnon scattering. As this three-dimensional system is more realistic than the ideal two-dimensional models, we believe that our results may also be relevant for future investigations on the non-linear excitations contribution to EPR linewidth in quasi-two-dimensional magnetic materials.

We have investigated the interactions between spin waves and vortex-antivortex pair and found exact solutions for zero modes and approximated solutions for the continuum states in a layered three-dimensional XY-model. Zero modes become apparent in inelastic neutron scattering experiments and essentially contributes in central peak due to interference between ones and vortex-pair. The vortex-antivortex interaction is linear for large distances of separation and the effective interplane coupling E₂(T) decreases with the temperature T, vanishing at T = T_c [3,6,9]. This mean that the interplane coupling effectively ceases to be felt by the vortices for T > T_c, the model effectively reducing to a two-dimensional planar model and free vortices start to exist and the discrete modes disappear giving rise to zero frequency states as the lower limit of a continuum of frequencies (Goldstone modes [19]). We believe that the local modes and the scattered modes obtained here may contribute to the renormalization of the vortex interaction. In fact, as it was shown in Ref. [20], the lowest order effect of vortex spin wave interactions can be described as a renormalization of the exchange constant. Besides, zero modes may be coupled to internal interaction of the vortices in a pair. Our calculations can be applied to any layered system with small interlayer coupling in which small oscillations and independent vortex pairs are present, such as in superconductors [21].

Acknowledgement

This work was partially supported by CNPq and FAPEMIG (Brazil).

• [1] J.M. Kosterlitz and D.J. Thouless, J. Phys. C 6 ,1181 (1973).
• [2] V. Cataudella and P. Minnhagen, Physica C 166, 442 (1990).
• [3] P. Minnhagen and P. Olsson, Phys. Rev. B 44, 4503 (1991).
• [4] M. Ito, Prog. Theor. Phys.66, (1981) 1129 (1981).
• [5] G.M. Wysin, M.E. Gouvęa, A.S.T. Pires, Phys. Rev. B 57, 8274 (1998).
• [6] B.V. Costa, A.R. Pereira, A.S.T. Pires, Phys. Rev. B 54, 3019 (1996).
• [7] S.K. Oh, C.N. Yoon, J.S. Chung, Phys. Rev. B 56 ,13677 (1997).
• [8] K. Nho and E. Manousakis, Phys. Rev. B 59, 11575 (1999).
• [9] A.R. Pereira, A.S.T. Pires, M.E. Gouvęa, Phys. Rev. B 51, 16413 (1995).
• [10] J.F. Currie, J.A. Krumhansl, A.R. Bishop, S.E. Trullinger, Phys. Rev. B 22, 477 (1980).
• [11] B.A. Ivanov, A.K. Kolezhuk, G.M. Wysin, Phys. Rev. Lett. 76, 511 (1996).
• [12] A.R. Pereira, F.O. Coelho, A.S.T. Pires, Phys. Rev. B 54, 6084 (1996).
• [13] C.E. Zaspel, J.E. Drumheller, Int. J. Mod. Phys. B 10, 3649 (1996).
• [14] A.R. Pereira and A.S.T. Pires, Phys. Rev. B 60, 6226 (1999).
• [15] S. Hikami and T. Tsuneto, Prog. Theor. Phys. 63, 387 (1980).
• [16] O. Hudák, Phys. Lett. A 89, 245 (1982).
• [17] A.S.T. Pires, A.R. Pereira, M.E. Gouvęa, Phys. Rev. B 49, 9663 (1994).
• [18] S.E. Trullinger and R.M. Deleonardis, Phys. Rev. A 20, 2225 (1979).
• [19] R. Rajaraman, Solitons and Instantons (North-Holland, Amsterdam, 1984).
• [20] A.R. Pereira, A.S.T. Pires, M.E. Gouvęa, Solid St. Commun. 86, 187 (1993).
• [21] O. Hudák, Phil. Magazine B 81, 1533 (2001).

Publication Dates

• Publication in this collection
  04 Dec 2002
• Date of issue
  Sept 2002

History

• Received
  10 June 2002