Higher derivative quantum gravity near four dimensions

Abstract

We investigate the role of the Gauss-Bonnet term for the n = 4 and n = 4-e renormalization group, for both conformal and general versions of the theory. The cancellation of the quantum effects of the Gauss-Bonnet term in the n = 4 limit represents an efficient test for the correctness of previous calculations and also resolves two long-standing problems concerning quantum corrections in quantum gravity. In the case of n = 4-epsilon renormalization group there is a number of new nontrivial fixed points, that may indicate to a rich nonperturbative structure of the theory. At the same time, if we do not treat e as a small parameter, the renormalization group is spoiled by an extensive gauge fixing ambiguity.

Higher derivative quantum gravity near four dimensions

Guilherme de Berredo-Peixoto; Ilya L. Shapiro^*

Departamento de Física – ICE, Universidade Federal de Juiz de Fora, Juiz de Fora, CEP: 36036-330, MG, Brazil

ABSTRACT

We investigate the role of the Gauss-Bonnet term for the n = 4 and n = 4-e renormalization group, for both conformal and general versions of the theory. The cancellation of the quantum effects of the Gauss-Bonnet term in the n = 4 limit represents an efficient test for the correctness of previous calculations and also resolves two long-standing problems concerning quantum corrections in quantum gravity. In the case of n = 4-e renormalization group there is a number of new nontrivial fixed points, that may indicate to a rich nonperturbative structure of the theory. At the same time, if we do not treat e as a small parameter, the renormalization group is spoiled by an extensive gauge fixing ambiguity.

It is well known that the conventional way of quantization of General Relativity leads to a non-renormalizable theory [1-3]. An alternative way of quantizing gravity is to introduce some higher derivative terms into a classical action, treating them at the same footing as the lower-derivative (Einstein-Hilbert and cosmological) terms, in such a way that the new quantum theory is renormalizable [4] (see also [5]). The renormalizability of higher derivative quantum gravity (HDQG) enables one to establish the asymptotic freedom in the UV limit [6-9] and explore the possible role of quantum gravity in the asymptotic behavior for GUT-like models [10] (see [11] for the general introduction to the subject).

The price for the renormalizability of HDQG is the unphysical pole in the spin-two sector of the tree-level propagator of the renormalizable quantum gravity. The pole corresponds to a state with negative kinetic energy or with a negative norm in the state space. Such unphysical states (massive ghosts) [4] have masses with a magnitude of the Planck order, still they spoil unitarity of the S-matrix, making the whole approach of HDQG rather doubtful. A number of attempts to overcome the problem of massive ghosts has been undertaken. In particular, one can construct ghost-free models of R²-type gravity with torsion [12], but the renormalizability is lost in these models [13]. A very interesting possibility is to investigate the non-perturbative structure of the theory, e.g., through the resummation of quantum corrections to the graviton propagator or through the 1/N approximation [14, 15]. Unfortunately none of these approaches can give definite answer related to the presence of ghost in the asymptotic states of the exact propagator [16]. However, due to the importance of the problem, it looks reasonable to consider other possible non-perturbative approaches to HDQG, in particular the n = 4-e renormalization group which proved to be a powerful tool in statistical mechanics [17], quantum field theory [18] and also in quantum gravity, where the n = 2-e approach was quite fruitful [19-22].

The classical action of HDQG in n = 4-e dimensions has the form

where µ is a dimensional parameter,

is the square of Weyl tensor, is the integrand of the Gauss-Bonnet term, which is topological (Euler characteristic) in n = 4, k² = 16pG, where G is the Newton constant, L is the cosmological constant and l, r, x, t are independent parameters in the higher derivative sector of the action. Without R²-term, the higher derivative sector of the theory possesses (in n = 4 case) local conformal invariance, hence this version represents special interest.

As far as our purpose is n = 4-e renormalization group, it is not correct to ignore the role of the Gauss-Bonnet term. Indeed this term is topological in four dimensions, but still it may play some important role at the quantum level, becoming very important for n ¹ 4. In the previous publications [23, 24] we have performed an explicit calculations taking this term into account and clarified this issue. Here we present, without much technical details, the general review of these works.

The nontrivial role of the Gauss-Bonnet term is known since the work of Capper and Kimber [25]. The topological nature of this term at n = 4 is closely related to its diffeomorphism invariance. However, when theory is quantized using the Faddeev-Popov procedure, this symmetry is broken such that the vector space extends beyond physical degrees of freedom. After quantization, not only spin-2, but also spin-1 and spin-0 components of quantum metric become relevant, and the topological term creates new vertices of interaction between these components. Therefore, the loops may be, in principle, affected by the presence of the topological term. One can expect that after including the topological term, the gauge-fixing condition should modify and eventually compensate the new vertices. Indeed, this is exactly what happens in n = 4 but of course not for 4-e, where we meet a non-trivial effect of the Gauss-Bonnet term in both conformal and general HDQG theories [23, 24].

The renormalization group equations in both n = 4 and n = 4-e cases are completely defined by the trace of the coincidence limit of the coefficient a₂(x,x') of the Schwinger-DeWitt proper-time expansion. However, in both cases these equations demonstrate an essential gauge-fixing ambiguity. In the framework of the background field method g_mn ® = g_mn+h_mn we introduce the general linear gauge fixing condition, such that the one-loop effective action is given by the expression [8]

where is bilinear (in the quantum fields) form of the action (1), taken together with the gauge-fixing term

_gh is bilinear form of the action of the Faddeev-Popov ghosts, µ is the renormalization parameter in dimensional regularization.

The gauge fixing condition c^m and and the weight operator Y_mn have the form

where a_i = (a, b, g, d) are arbitrary gauge-fixing parameters. The action of the Faddeev-Popov ghosts is

The gauge-fixing dependence of the effective action in HDQG has been considered in [8, 24, 26]. We denote G(a_i) the effective action corresponding to arbitrary values of gauge parameters a_i and G_m = G() calculated for special values of these parameters, . Our purpose is to evaluate the expression for the difference between the two effective actions G(a_i)-G_m. Despite this expression may be rather complicated [26], the local part of it (which is the only one relevant for the renormalization group in the -scheme which we use here) may be easily evaluated without special calculations. For this end we remember that the gauge dependence of counterterms has to disappear on the classical mass-shell. Hence we can write

where f_mn (a_i) is some unknown function. The integration is taken over n-dimensional space, because our target is the renormalization group in n = 4-e dimensions.

The object of our interest here is the local part of the effective actions G_m and G(a_i), both have the same dimension as the classical equations of motion dS/dg_mn. Therefore f_mn (a_i) is a symmetric dimensionless tensor and the unique choice for it is f_mn (a_i) = g_mn·f(a_i) where f(a_i) is a numerical quantity. Thus we arrive at the relation

The gauge-fixing dependence is proportional to the trace of classical equations of motion. Simple calculation [24] for an arbitrary n yields the following result:

For n = 4 the coefficients of the E, C² and R² terms are gauge-fixing invariant [26]. Consequently the corresponding renormalization group equations are universal, providing information about the UV limit of the theory. At the same time, (R)-type pole is gauge-fixing dependent and therefore the parameter t in (1) is not an essential one. The immediate conclusion is that there is no much interest to calculate the renormalization of t, especially if the calculation is done for a particular gauge-fixing. The renormalization of Einstein-Hilbert and cosmological terms is gauge-fixing dependent, but the dimensionless combination k²L is an essential coupling constant with invariant renormalization relation.

In the n = 4-e case the situation is more complicated. An important consequence of the eq. (8) is that neither one of the parameters x,y,z,t,k,L is essential in the n = 4-e case. However, gauge-fixing dependence is concentrated in a single numerical function f(a_i) and therefore we can easily extract combinations of the couplings which are essential parameters.

The calculational details can be found in [23] for the conformal quantum gravity and in [24] for the general version including the Einstein-Hilbert sector. The expression for the divergent part of the 1-loop effective action is

functions of n, different for the conformal [23] and general [24] cases of HDQG.

In the conformal case, after taking the n ® 4 limit in the coefficient of the pole term, we obtain

The coefficients in the above expression coincide with the ones Fradkin and Tseytlin [8] and later on by Antoniadis, Mazur and Mottola [27]. At the same time we observe there is no ò

R²-type divergence [8] and hence there is no need to apply the conformal regularization [28, 29] in order to obtain multiplicatively renormalizable conformal theory at one loop order.

Despite the one-loop divergences are conformal invariant, this symmetry is broken at the one-loop level in the finite part of the effective action. The divergences of the ò

C² and ò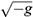E-type produce the anomalous violation of the Noether identity,

where and a' = a'(a_i,...) is some function of arbitrary gauge fixing parameters [26], which contains also an additional arbitrariness [30]. At the level of one-loop effective action we meet the well-known form of the quantum correction to the classical action of conformal HDQG [26, 31]

Here D₄ = 2+ 2R^mnÑ_mÑ_n - R + (Ñ^m R)Ñ_m is the four derivative conformal invariant operator acting on the dimensionless scalars and the two such scalars j and y are auxiliary fields.

An interesting question is whether the renormalizability of the conformal invariant version of HDQG will be broken at higher loops. In this respect the mentioned arbitrariness in the one-loop ò

R²-type contribution gains special importance. The remarkable difference between this case and the standard semiclassical one is that in the last case the ò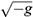R² belongs to the action of external field and one is always free to introduce this term with an arbitrary coefficient already at the classical level. In conformal quantum gravity, introducing such term would completely change the physical content of the theory. Hence we can not fix the arbitrariness by fixing the renormalization condition for the ò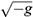R² term and therefore higher loop non-conformal counterterms (except leading log's, of course) are also arbitrary. It is difficult to make definite conclusion concerning renormalizability in this situation.

Our results show, anyway, that the conformal quantum gravity can be regarded as a good approximation. The corresponding procedure means that one can start from the theory with a very small coefficient of the ò

R² term. Due to the one-loop renormalizability of the conformal theory this coefficient will remain very small at the quantum level. If we consider the conformal quantum gravity in this framework, the problem of ambiguity of the anomalous ò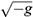R² term is irrelevant and we can regard this theory as a useful particular example of the higher derivative quantum gravity models.

In the general non-conformal case of HDQG the n ® 4 limit, the pole term has the form

This result perfectly agrees with the one of Avramidi and Barvinsky [9]. This coincidence shows that the effect of the Gauss-Bonnet term is not relevant for the one-loop renormalization.

Despite the r-dependence cancels out in the e ® 0 limit, the 4-e renormalization group equations do not assume exactly the form of the known equations in four dimensions, and the e-dependence is not simple, because the 4-e b-functions are sensitive to (e)-corrections which depend on r. In fact, the situation with 4-e renormalization group equations is even more complex, because one has to account for the arbitrariness coming from the choice of a gauge-fixing condition. Taking the gauge-fixing arbitrariness (8) into account, we arrive at the complete form of 4-e renormalization group equations for the three parameters

Our strategy concerning the issue of gauge fixing dependence will be as follows. We construct two essential parameters - some combinations q and w of the effective charges (l,r,x). Let us take q = l/r , w = - 3l/x. The coefficient -3 in the second expression provides correspondence with the notations of [8, 9]. The renormalization group equations for these parameters are free from the gauge-fixing ambiguity. The equations for the charges q and w will be explored in order to establish the UV stable fixed points. After that we shall consider the equation for the remaining effective charge, with the invariant combinations q and w at the fixed point. In this way we can learn the asymptotic UV behaviour corresponding to a given fixed point.

According to (14), the renormalization group equations for q and w are independent on the gauge arbitrariness and have the following universal form:

Here t(t) is a new parameter defined by

where l(t) is a solution of the renormalization group equations (see [24]). For a while we assume that the limit t ® ¥ corresponds to the UV limit t ® ¥ , as it was in the standard n = 4 renormalization group.

The numerical investigation of the equations (15) has been performed for a special small values of e. This analysis has shown a number of new fixed points, which do not have place in the four dimensional case. We can meet non-Gaussian new fixed point which are stable in both UV and IR and also saddle point - type fixed points. One can consider this as an indication to a possible rich non-perturbative structure of the theory. We present the fixed points for one particular case in Table 1.

The physical interpretation of these fixed points is not a simple matter. In order to understand the situation better, let us consider the analytical form of l(t) in the vicinity of some fixed point (w₀,q₀). For this end, the expression b₂ must be rewritten in terms of w and q, which should be further replaced by w₀ and q₀. After performing this, independent on the values of w₀ and q₀ we arrive at the equation

where

Let us remark that the parameter b in the last equation depends only on the values (w₀ ,q₀), while the parameter a depends also on the choice of a gauge-fixing condition and therefore can be made arbitrary.

The solution of eq. (17) is straightforward

Starting from this relation, we integrate (16) and arrive at the explicit form of t

where C is an irrelevant integration constant. It is easy to see that the assumption of t ® ¥ in the UV is not correct, for it depends on the gauge fixing here. Indeed, this means that the physical interpretation of the 4-e renormalization group is not a simple matter, obviously it can not be achieved through the calculations only.

Let us remember that the successful application of the 4-e renormalization group is essentially non-perturbative and therefore it is not a trivial issue to combine this approach with the one-loop approximation. Indeed the consideration of this sort may be justified only in case there are no other more reliable access to a non-perturbative regime (HDQG is exactly the case) and it is not a surprise it requires an additional input anyway. If we want consider 4-e renormalization group simultaneous with the one-loop approximation, the quantity e must be considered small by definition and only linear effects in e can be taken into account. If we accept this view, the problem of "total" gauge fixing dependence gets solved and we meet an asymptotically free theory with nontrivial fixed points. Only a real non-perturbative treatment, however, can help to give definite answer about whether these new fixed points really take place or whether the quantum corrections to the graviton propagator has desirable form. The situation is, therefore, quite similar to the one with another "nonperturbative" approaches to HDQG.

Acknowledgments

One of the authors (G.B.P.) is grateful to Departamento de Física at the Universidade Federal de Juiz de Fora for kind hospitality. The work of the authors has been supported by the fellowship from CAPES (G.B.P.) and various research grants from CNPq and FAPEMIG.

References

[1] G. t'Hooft and M. Veltman, Ann. Inst. H. Poincare. A 20, 69 (1974).

[2] S. Deser and P. van Nieuwenhuisen, Phys. Rev. D 10, 401 (1974); D10, 411 (1974).

[3] M. H. Goroff and A. Sagnotti, Nucl. Phys. 266B, 709 (1986).

[4] K. S. Stelle, Phys. Rev. D 16, 953 (1977).

[5] B. L. Voronov and I. V. Tyutin, Sov. J. Nucl. Phys. 39, 998 (1984).

[6] J. Julve and M. Tonin, Nuovo Cim. B 46, 137 (1978).

[7] A. Salam and J. Strathdee, Phys. Rev. D 18, 4480 (1978).

[8] E. S. Fradkin and A. A. Tseytlin, Nucl. Phys. B 201, 469 (1982).

[9] I. G. Avramidi and A. O. Barvinsky, Phys. Lett. B 159, 269 (1985); I. G. Avramidi, Sov. J. Nucl. Phys. 44, 255 (1986); I. G. Avramidi, (Ph.D. thesis, Moscow University, 1986); [hep-th/9510140].

[10] I. L. Buchbinder and I. L. Shapiro, Sov. J. Nucl. Phys. 44, 1033 (1986); I. L. Buchbinder, O. K. Kalashnikov, I. L. Shapiro, V. B. Vologodsky, and Yu.Yu. Wolfengaut, Phys. Lett. B 216, 127 (1989); I. L. Shapiro, Class. Quant. Grav. 6, 1197 (1989).

[11] I. L. Buchbinder, S. D. Odintsov, and I. L. Shapiro, Effective Action in Quantum Gravity (IOP, Bristol, 1992).

[12] D. E. Neville, Phys. Rev. D 18, 3535 (1978); D21, 867 (1980); E. Sezgin and P. van Nieuwenhuizen, Phys. Rev. D 21, 3269 (1981); E. Sezgin, Phys. Rev. D 24, 1677 (1981).

[13] I. L. Shapiro, Phys. Repts. 357, 113 (2002); [hep-th/0103093].

[14] E. T. Tomboulis, Phys. Lett. B 70, 361 (1977).

[15] E. T. Tomboulis, Phys. Rev. Lett. 52, 1173 (1984); Phys. Lett. B 97, 77 (1980); I. Antoniadis and E. T. Tomboulis, Phys. Rev. D 33, 2756 (1986).

[16] D. A. Johnston, Nucl. Phys. B 297, 721 (1988).

[17] K. G. Wilson and M. E. Fisher, Phys. Rev. Lett. 28, 240 (1972); K. G. Wilson and J. B. Kogut, Phys. Rept. 12, 75 (1974).

[18] K. G. Wilson, Phys. Rev. D 7, 2911 (1973).

[19] R. Gastmans, R. Kallosh, and C. Truffin, Nucl. Phys. B 133, 417 (1978).

[20] S. M. Christensen and M.J. Duff, Phys. Lett. B 79, 213 (1978).

[21] S. Weinberg, in: General Relativity. ed: S. W. Hawking and W. Israel (Cambridge. Univ. Press. 1979).

[22] H. Kawai and M. Ninomiya, Nucl. Phys. B 336, 115 (1990).

[23] G. de Berredo-Peixoto and I. L. Shapiro, Phys. Rev. D 70, 044024 (2004).

[24] G. de Berredo-Peixoto and I. L. Shapiro, Phys. Rev. D 71, 064005 (2005).

[25] D. M. Capper and D. Kimber, Journ. Phys. A 13, 3671 (1980).

[26] I. L. Shapiro and A.G. Jacksenaev, Phys. Lett. B 324, 286 (1994).

[27] I. Antoniadis, P. O. Mazur, and E. Mottola, Nucl. Phys. B 388, 627 (1992).

[28] F. Englert, C. Truffin, and R. Gastmans, Nucl. Phys. B 117, 407 (1976).

[29] E. S. Fradkin and G. A. Vilkovisky, Phys. Lett. B 73, 209 (1978).

[30] M. Asorey, E. V. Gorbar, and I. L. Shapiro, Class. Quant. Grav. 21, 163 (2003).

[31] R. J. Reigert, Phys. Lett. B 134, 56 (1980); E. S. Fradkin and A. A. Tseytlin, Phys. Lett. B 134, 187 (1980).

Received on 13 October, 2005

*

Also at Tomsk State Pedagogical University, Russia

Publication Dates

• Publication in this collection
  16 Jan 2006
• Date of issue
  Dec 2005

History

• Received
  13 Oct 2005