Electron trajectories in a helical free-electron laser

a21v32n3

Electron Trajectories in a Helical Free-Electron Laser

Riadh EL-BAHI, Mohamed Nazih Rhimi, and Abdel Wahab Cheikhrouhou

Department of Physics, Faculty of Sciences,

University of Sfax, B.P 802, Sfax 3018, Tunisia

Received on 8 November, 2001. Revised version received on 9 May, 2002.

A description is made of electron trajectories in a magnetic field consisting of helical wiggler and a uniform axial guide field. The explicit motion of particles for which the quadratic approximation to the Hamiltonian was carried out in some previous publications is now presented. The transverse position as a function of time is essentially the superposition of three circular motions of different frequency; one corresponds to the fixed point, the second to the cyclotronic motion, while the third is a very slow motion of the center of gyration. Electrons in this model swept out the x - y plane with elliptical and circular orbits that characterize the group I, the normal and reversed-field group-II configurations. Several illustrative examples are discussed in detail.

I Introduction

The calculation of the trajectories of electrons in a Free Electron Laser (FEL) with a helical wiggler field and a uniform axial guide field has been the subject of many researches [1-11], in particular when the spatial dependence of the wiggler field is included. It was established in early works that a particular case of steady motion exists, in which the electrons follow an axially centred helical path with constant axial velocity in such a way that the transverse velocity vector of the electron is parallel or anti-parallel to the transverse magnetic field at each point. Of course, now electron is likely to follow this ideal trajectory, and the question of what the non-ideal trajectories look like arises. Freund and Ganguly [3] have studied the equations of motion in the neighborhood of the ideal trajectory, and have obtained two squared frequencies, which characterize the oscillations of the electrons about it. Rhimi et al [1] have extended this work by using guiding centers coordinates showing that the transformed linear momentum is conserved along any trajectory as a consequence of the screw-displacement symmetry of the magnetic field. For a given electron, one determines its value from the initial conditions, and provided certain conditions are met, a fixed point of the Hamiltonian exists. The Hamiltonian is then expanded about the fixed point, and its quadratic term may be reduced by the use of the properties of the "rotational'' variable to two uncoupled harmonic oscillators of characteristic frequencies _± and constant amplitudes | _± ( = 0 ) |².

In this paper, we continue the work of Refs. [1] and [11] with the study of the trajectories described by those harmonic oscillators. In order to investigate the performance of FELs, we have developed a theoretical study of the trajectories then written a code based on the former works, that evaluates numerically the orbits of the particle in both space and velocity configurations. The code HOTA (Harmonic Oscillator Trajectory Approximation) [12] using the theoretical approach of Refs. [1] and [11] is a MAPLE V (Release-4) program that given the initial conditions of both the FEL and the beam parameters, gives the electron trajectory as output.

This introduction is followed by a section devoted to the calculation of the orbits. In Section III, a simple Approximative description of the trajectories is given. Before the conclusion comes Section IV, which brings out the essence of the theoretical work with a numerical application.

II Calculation of the orbits

The explicit calculation of the motion of an electron for which the quadratic approximation to the Hamiltonien is adequate proceeds as follows. It is necessary to compute its axial position 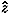( 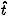). The axial velocity is found to be [1] :

First, we insert into Eq. (1) the explicit time dependence of the variables

_f and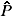 _y . Second, a subsequent integration yields the axial position as a function of time,

In this expression, b_z0 is the value of the axial velocity at the fixed point, and the quantities db_z (time-independent correction) and E_k may be written as follows :

where we follow the same notation of Ref. [11] for homogenity reasons.

The expression of

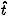given by Eq. (2) shows that if any of the three quantities _– , ₊± _– are very small, the deviation from the ideal position coordinate may become appreciable even if the amplitudes | _± | are acceptably small. Consequently, the operating conditions should be chosen so as to avoid this difficulty. Since _– vanishes at the limits of stability, it is clear that operation too close to the limits is likely to be unsuccessful. The difference ₊ – _– becomes small in the region where the frequencies attempt to cross hence this is also an unsuitable operating region.

Once the longitudinal coordinate 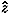(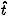) of Eq. (2) has been computed, Eq. () of Ref. [1] provides us with explicit expression for the transverse position:

where by

_± we mean the time dependent values | _± | e ⁱ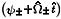. We observe that the transverse motion consists of linear superposition of five circular motions, one that corresponds to the ideal axially centered helical motion 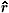₀ , and four that are linear in the oscillator amplitudes. The phase of the principal circular motion is 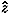(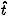). Since Eq. (2) has oscillatory pieces in addition to the term linear in time, the true time dependence of 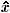+ 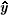is quite complex, and the Fourier spectrum involves several frequencies.

The transverse velocity of the electron may be evaluated. Computing the time derivative of the transverse position coordinate (Eq.(10)), we obtain the following expression:

III Simple approximate description of the trajectories

The preceding treatment has considered in great detail the most general motion, which our model can predict. In this section we present a simplified approximate description of the trajectories. We obtain this by setting equal to zero a certain number of quantities, which are numerically quite small over a certain domain of parameters. What emerges, at least in the favorable situations, is a quantitatively correct but quite simple description of the trajectories in term of the ideal helical motion accompanied by a very slow rotation of the instantaneous center of gyration as well as a parasitic cyclotronic motion. The axial velocity of an electron oscillates about its ideal value at a single frequency, giving rise to a fairly simple Fourier spectrum for the transverse motion. In Ref. [3], Freund and Ganguly have presented a thorough description of these orbits, and of the perturbed trajectories, which remain in their vicinities. They establish the essential relation between the longitudinal and transverse velocities. Writing | | = n_^/n_z, they find:

where I₁ denotes the modified Bessel function of order 1. Positive corresponds to trajectories of group II, with [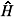₀b_z0 < ₀ , whereas negative corresponds to trajectories of group I, with 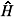₀b_z0 > ₀ .

Although the motion we predict in general may be quite complex, inspection of our Figs. 1-4 of Ref. [11] shows that for certain ranges of scaled radius | 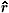₀ |, all but two of the coefficients a_±f , etc., are quite small. Next, we note that in general

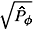, and it might be reasonable to neglect it. If we also take into account the fact that one of the frequencies _± is almost equal to the axial velocity at the fixed point, we obtain a greatly simplified description of motion. Two cases can be presented:

First case: If

₀b_z0 > ₀ we may use +» b_z0 ,

and all others zero. For the shift in mean longitudinal velocity we find:

which implies that increasing the oscillator amplitude

₊ produces a small increase in speed, while increasing _– has the opposite effect.

All the quantities E_k are zero expect

which implies that the ripple in longitudinal speed is caused by the

_– amplitude, and has the frequency _– . The axial position is given by:

The transverse position is then given by :

which corresponds to a superposition of three circular motions, one of which is the projected ideal helical motion of scaled radius |

₀ |, while the other two have scaled radii of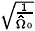 | ₊ | and 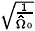| _– |, respectively. If we neglect the ripple and shift of b_z0 , then the three circles are swept out uniformly in time at the respective frequencies b_z0 , b_z0 – ₊ and b_z + _– . Taking into account the near equality of b_z0 and ₊ , we see that the amplitude ₊ corresponds to an extremely slow rotation. This has been described in the literature as the guide center motion [3], about which the more rapid circular motions occur. 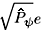The radius of the circle described by the guide center is determined by |₊ |, which is essentially the modulus of the initial value of our dynamical variable e^iy – i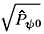 . The desired FEL motion then occurs about this displaced guide center, and is accompanied by the additional circular motion at the frequency b_z0 + _– . 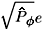The radius of this cyclotronic motion is thus determined by _– , which is essentially given by the modulus of the initial value of ^if 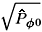– . Thus our simple description leads to an interpretation of the transverse motion as a superposition of three circular movements: first the ideal helical motion; second, a very slow motion of the guide center; and third, a cyclotron motion, this being also the cause of the ripple in the longitudinal velocity. This description applies to both group I and that part of group II above the transition region, the only difference being that _– is negative in the former and positive in the latter.

Second case: If

₀b_z0 < ₀ , which occurs typically for small positive values of 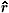₀ , we have _–» b_z0 , a _{+ f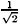} = , a _{– y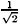} = – , and all others zero. Now the shift in mean longitudinal velocity is given by

which shows that the oscillator amplitude

_– always contributes a positive shift, whereas the contribution of the amplitude ₊ produces a negative shift when b_z0 > 0, but can have either sign when b_z0 < 0. The effect on the mean longitudinal speed of increasing | _– | is thus an increase in normal group II operation. Increasing | [₊ | always reduces mean speed in normal group-II operation. In the reversed-field configuration an increase in | ₊ | reduces the mean speed if the quantity b_z0

₊£ - 1/2 and increases it otherwise.

All E_k are zero except

which mean that the ripple in b_z0 is caused mainly by the + amplitude, and has the frequency + . The axial position is given by

The transverse position is then given by :

which again corresponds to a superposition of three circular motion just as in the previous case. If we again neglect the ripple and shift of b_z0 , then the three circles are traced out at the respective frequencies b_z0 , b_z0 + ₊ and b^z₀ – _– . Taking into account the near equality of b_z0 and _– , we see that now the amplitude _– corresponds to the slow rotation of the guide center. Here | _– | is essentially the modulus of the initial value of our dynamical variable 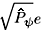e^iy - i 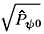. 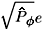The radius of the cyclotronic motion is now determined by | ₊ |, which is again given by the modulus of the initial value of ^if 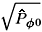– . We thus find essentially the same description as in the previous case, except that here bz₀ can be negative. The validity of this description, which applies to group-II motion below the transition region, is somewhat greater than in the preceding case, since here the stability limits are not approached. However, the helical orbits have rather small radii, which means that the transverse motion caused by the parasitic cyclotron and guide center amplitudes may be of the same order of magnitude as the desirable FEL motion.

IV Particle orbits

This section is a numerical application of precedent theoretical treatment. Four examples were chosen to sweep the different group configurations. Figure 1 illustrates the reversed field group-II mode with the following parameters (the electron beam kinetic energy is 1.05 ( in units mc² ) ,B_w / B₀ = 0.05 and 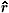₀ =0.05 ). In Fig. 1a the behavior is exceedingly simple, in fact the nearly circular projection of the trajectory on the transverse plane corresponds to a superposition of three circular motions giving then a nearly ideal trajectory. In particular, the rotation of the guiding center is due to the near equality of the oscillator frequency ( _– =-0.002809) and the frequency of the fixed point (-0.002813). In this favorable situation we show in Figs. 1b and 1c that the oscillations of longitudinal and transverse velocities are regular. However, the helical orbits have rather small radii, which means that the transverse motion caused by the parasitic cyclotron and guiding center amplitudes may be of the same order of magnitude as a desirable FEL motion. Consequently, the trajectories in the reversed-field mode are recognized to be quite well behaved.

The second example shows in Fig. 2 an electron whose initial conditions are far from the ideal trajectory illustrating the experimental results obtained by Conde and Bekefi [13], who have studied the reversed field configuration. In this case, the beam kinetic energy is 1.75 (in units mc²), and the ratio B_w / B₀ =0.118. It should be mentioned that the exceedingly small ripple in the axial velocity db_z = 0.012 in Fig.2.a may be attributed partly on the one hand to the small oscillator amplitude ( | ₊ |=0.1, ₊ =1.39 ) and on the other hand to the smallness of the dimensionless radius of the fixed-point helical orbit in the reversed-field configuration (0.0489). However, the transverse velocity v_x (Fig.2b) is not a simple oscillation, and the trajectory in the transverse plane does not resemble a circle. The transverse position as a function of time is essentially the superposition of three circular motions of different frequency: One is the fixed-point motion, the second is the ₊ oscillator which sweeps out a circle at effective frequency ₊ +b_z0 while the third is the _– oscillator which sweeps out a circle at effective frequency _z0 – _– . Since b_z0 = - 0.814, ₊ =1.39 and _– =-0.817, we are in the second case ( _–» b_z0 ), the effective frequencies are -0.814, 0.576, 0.003, respectively. The third frequency is so small that nothing is swept out and the only effect is that the center of the fixed point circle is displaced from the center of the wiggler.

In the normal group II, beyond

₀ = 1, for B_w/B₀ = 0.2, near the limits of stability, where _– vanishes, the simple approach of Ref. [11] is not even approximately valid. Certainly, all the coefficients of the normal mode become significant, a _{+ f} = 0.506, a ₊ f^_* = 0.205, a _{+ y} = 0.540 et a ₊ y^_* = - 0.078 (see Ref. [11]). Under these circumstances, the full complexity of our general treatment is needed to describe the trajectories. The ripple in the axial speed becomes more complex (Fig. 3a) while an additional circular motion complicates the transverse motion. However, the longitudinal velocity v_z in Fig. 3a is not a simple oscillation, and the transverse velocity v_x is roughly regular (Fig. 3b), the trajectory in the transverse plane of Fig. 3c does not resemble a circle. Taking into account the rough equality between the dimensionless frequency of fixed point 0.4330 and the oscillator frequency ₊ =0.4427 , then ₊» b_z0 , the motion is but a rapid rotation of the guiding center. This result confirms the first case (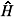0b_z0 > ₀ ).

On the basis of Fig. 4, we infer that group-I motion presents no particular difficulties since the transverse plane describe/ a pseudo-circular motion (quasi-constant gyroradius = -0.35) (see Fig. 4a). This advantageous situation requires either high energy 3 (in units mc²) or high wiggler field B_w / B₀ = 0.5. In this case, the fixed point frequency 0.8921 is roughly equal the oscillator frequency ₊ = 0.9520, the quasi-circular guiding center transverse motion is preferable since the trajectory is close to the steady-state orbits and the axial (Fig. 4b) and transverse (Fig. 4c) velocities have less ripple.

V Conclusion

The aim of this paper is to point out that, while a powerful calculation of the trajectory is certainly needed to investigate the details of the interaction between the electrons and the non magnetic effects in an FEL, the approximate but analytical approach of Refs. [1] and [11] is capable of providing a good description of trajectories, and its results can be easily interpreted.

• [1] M. N. Rhimi, R. El-Bahi, and A. W. Cheikhrouhou, Can. J. Phys. 78, 1069 (2000).
• [2] R. E. Aamodt, Phys. Rev. A 28, 2895 (1983).
• [3] H. P. Freund and A. K. Ganguly, IEEE J. Quant. Electr. 7, 1073 (1985).
• [4] J. Fajans, D. A. Kirkpatrick, and G. Bekefi, Phys. Rev. A 32, 3448 (1985).
• [5] C. Chen and R. C. Davidson, Phys. Fluids B 2, 171 (1990).
• [6] C. Chen and R. C. Davidson, Phys. Rev. A 43, 5541 (1991).
• [7] L. Wang. D. L. Bosley and J. Kevorkian, Physica D 88, 87 (1995).
• [8] L. Wang and J. Kevorkian, Phys. Plasmas 3, 1162 (1996).
• [9] V. L. B. de Jesus, A. P. Guimraes, and I. S. Oliveira, Braz. J. Phys. 29, 541(1999).
• [10] P. W. Milloni and J. H. Eberly, Lasers (Wiley, New York, 1998).
• [11] R. El-Bahi, M. N. Rhimi, and A. W. Cheikhrouhou, Braz. J. Phys. 31, 473 (2001).
• [12] R. El-Bahi, Ph. D. Thesis, University of Sfax, 2002 (unpublished).
• [13] M. E. Conde and G. Bekefi, Phys. Rev. Lett. 67, 3082 (1991).

Publication Dates

• Publication in this collection
  04 Dec 2002
• Date of issue
  Sept 2002

History

• Received
  08 Nov 2001
• Accepted
  09 May 2002