Shot noise in the presence of spin-flip scattering

Abstract

Shot noise is a time-dependent current uctuation due to the discrete character of the electron charge. Here we address shot noise in a spin-resolved tunneling system under the influence of spin-flip scattering within a master equation approach. We find that the average current <FONT FACE=Symbol>á</font>I<FONT FACE=Symbol>ñ</FONT> and Fano factor gamma("normalized noise") present contrasting behavior for differing spin-flip time ratios: <FONT FACE=Symbol>á</FONT>I<FONT FACE=Symbol>ñ</FONT> decreases while gamma increases for <img src="http:/img/fbpe/bjp/v32n2a/a20img03.gif" align="absMiddle"> > <img src="http:/img/fbpe/bjp/v32n2a/a20img01.gif" align="absMiddle"> as compared to the <img src="http:/img/fbpe/bjp/v32n2a/a20img03.gif" align="absMiddle"> = <img src="http:/img/fbpe/bjp/v32n2a/a20img01.gif" align="absMiddle"><FONT FACE=Symbol> </FONT>case and vice versa for <img src="http:/img/fbpe/bjp/v32n2a/a20img03.gif" align="absMiddle"><FONT FACE=Symbol> </FONT>< <img src="http:/img/fbpe/bjp/v32n2a/a20img01.gif" align="absMiddle">.

a20v322a

Shot Noise in the Presence of Spin-Flip Scattering

F.G. Brito and J.C. Egues¹

Departamento de Física e Informática, Instituto de Física de São Carlos,

Universidade de São Paulo, 13560-970 São Carlos, São Paulo, Brazil

Received on 23 April, 2001

Shot noise is a time-dependent current uctuation due to the discrete character of the electron charge. Here we address shot noise in a spin-resolved tunneling system under the influence of spin-flip scattering within a master equation approach. We find that the average current áIñ and Fano factor g ("normalized noise") present contrasting behavior for differing spin-flip time ratios: áIñ decreases while g increases for > as compared to the = case and vice versa for < .

Spin-dependent transport in tunneling structures is a fascinating subject. So far the bulk of experimental and theoretical investigations has been on metallic layered systems. This focus in now turning to more versatile semiconductor heterostructures. More specifically, spin-polarized transport - an obvious possibility in spin-dependent geometries [1] - has just recently been achieved in Mn-based II-VI and III-V doped semiconductor diodes [2,3,4]. These seminal experiments open up new venues for further advances in the emerging field of spintronics in semiconductors - where the spin of the carrier, rather than its charge, runs the show [5,6].

So far spin injection [2,3,4] has been demonstrated only at low temperatures and in the diffusive limit[7]. Spin injection at room temperatures, relevant for real device applications, remains a challenge. However, investigations at low temperatures are fundamentally important for understanding general features/properties of spin-polarized transport which may turn out relevant at high temperatures. Conceivably, some detrimental spin-flip effects contaminating low temperature transport may very well survive at higher temperatures.

Here we investigate spin-flip effects on transport through a spin-resolved tunneling system [8], Fig. 1. More specifically, we are interested in spin-flip effects on shot noise. Shot noise is a dynamic current fluctuation arising from the particular (or granular) nature of the electron charge. Shot noise investigations have become a major subject of research in the last decade or so [9,10]. Common wisdom has it that shot noise measurements supplement information contained in the average current. Here in particular we find that spin-flip processes affect the average current and shot noise in a contrasting fashion; in a limited parameter range, while shot noise is suppressed the average current is enhanced and vice versa, Fig. 2.

Physical system. We consider a II-VI double-barrier tunneling structure with a Manganese-based quantum well/dot. In the presence of an external magnetic field, the s-d exchange interaction between a traversing electron and the d electrons of the Mn gives rise to a spin-dependent quantum well/dot potential. This in turn lifts the spin-up/spin-down degeneracy of the resonant level. Each exchange-split resonant level accepts electrons with only a well-defined spin component. Fig. 1 schematically shows the system geometry. In Fig. 1, the many possible electron transitions connecting the emitter, spin-split levels ("islands" up and down) and collector are described by transition rates proportional to 1/t, where t is, roughly speaking, the respective transition time. Observe that the hops between spin-resolved levels in Fig. 1 involve spin flip. Here we use distinct spin-flip times for the up-to-down and down-to-up transitions between the islands, i.e.,¹ ; this is certainly the case when the relevant spin-flip mechanism connecting the islands is the s-d exchange interaction [11]. Our description, however, does not rely on any specific form of the spin-flip mechanism.

Semiclassical description. We model spin-resolved tunneling through a quantum well/dot in terms of classical hops among emitter, spin-split levels and collector as shown in Fig. 1 (see also inset in Fig. 2). Our approach is based on rate equations for the ensemble averaged number of electrons n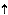(t) and n_¯(t) in the islands up and down, respectively. These equations are directly derived from the system population master equation describing the probability p(n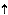,n_¯,t) of finding n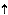and n_¯electrons in the islands at time t. Island up (down) holds at most N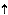(N_¯). Our transition rates take into account that no electrons can hop into a full island ("Pauli principle") or out of an empty one. This type of correlation does affect current fluctuations arising from the discreteness of the electron charge.

Average current and its fluctuations. From the rate equations mentioned above we can easily determine the average current through the system. In the steady state áIñ = eán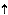ñ/t_c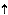+eán_¯ñ/t_c¯ (e: electron charge) and the average occupations án,_¯ñ = n

_,¯(t® ¥) depend on the several hoping times t's and N

_,¯. The current fluctuation is defined in terms of the ensemble average current-current correlation function á di(t+t^¢) di( t^¢) ñ . Experimentally, the relevant quantity is the spectral power of the shot noise measured (usually) at zero frequency, i.e., S(0) = 2ò ádi( t+t^¢) di( t^¢) ñ dt. By introducing appropriate "hop-hop" correlation functions, which describe how likely a particular hop follows a previous one, we can relate S(0) to the variance matrix of the system [12]. This 2×2 matrix is directly obtained from the master equation of the system. 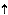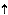The resulting expressions for the zero-frequency shot noise S(0) and the elements of the variance matrix (ádndn_¯ñ=ádn_¯ dn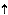ñ,á(dn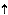)²ñ, and á( dn_¯) ²ñ) are too lengthy to be shown here [13].

Results and discussions.Fig. 2 displays curves for both áIñ/e (symbols) and the Fano factor g = S(0)/2eáIñ (lines) for the resonant-tunneling system in Fig. 1, with differing spin-flip time ratios. The normalizing factor 2eáIñ, usually called 'classical or full' shot noise (Schottky), denotes the shot noise power spectral density for a stream of uncorrelated electrons with average current áIñ. The Fano factor is a convenient means to assess how correlations affect shot noise. In Figure 2 both average current and Fano factor are strongly affected by spin-flip processes. This can be more clearly observed for t_c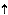/t_e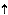in the range 1 to 10 (or, equivalently, 0 to 1 in the horizontal log axis of Fig. 1) in which the flow of electrons from 'island-up' to the collector is suppressed. In this case, to arrive at the collector an electron has to necessarily go through 'island-down' thus undergoing spin flip. In this particular range, shot noise (Fano factor) and average current exhibit contrasting behavior for differing /ratios; áIñ decreases while g increases for > as compared to the = case and vice versa for < . This trend is reversed in the [-1,0] range. Hence shot noise and the average current are distinctively sensitive to spin flip.

Sumarizing, we have discussed spin-flip effects on spin-dependent transport in semimagnetic junctions with spin-split resonant levels. Our semiclassical description in terms of rate and master equations allows us to calculate both the average current and shot noise; the latter in terms of the variance matrix of the system. Interestingly enough, we find that the average current and shot noise are sensitive to spin flip (between the spin-split levels) in a contrasting way. In a limited parameter range, while the average current decreases (increases) the shot noise increases (decreases) as function of the ratio/.

This work has been supported by FAPESP. F. G. Brito acknowledges a fellowship from CNPq.

Present address: University of Basel, Institute of Physics, Klingelbergstrasse 82, CH-4056 Basel, Switzerland.

References

[1]J. C. Egues, Phys. Rev. Lett. 80, 4578 (1998). For recent related works see Y. Guo et al., J. Appl. Phys. 88, 6614 (2000); Y. Guo et al., Phys. Rev. B 63, 214415 (2001); P. F. Farinas, Phys. Rev. B 64, 161310(R) (2001); K. Chang and F. M. Peeters, Solid State Commun. 120, 181 (2001); and Ref. [7] below.

[2]R. Fiederling M. Kleim, G. Reuscher, W. Ossau, G. Schmidt, A Waag, and L. W. Molenkamp, Nature 402, 787 (1999).

[3]Y. Ohno D. K. Young, B. Beschoten, F. Matsukura, H. Ohno, and D. D. Awschalom, Nature 402, 790 (1999).

[4]B. T. Jonker Y. D. Park, B. R. Bennett, H. D. Cheong, G. Kioseglou, and A. Petrou, Phys. Rev. B 62, 8180 (2000).

[5]G. Prinz, Science 282, 1660 (1998).

[6]N. Samarth and D.D. Awschalom, Quantum Devices and Circuits, edited by Ismail, K.; Bandopadhyay, S.; Leburton, J.P.; (1997).

[7]For a theoretical discussion of possible unique signatures for coherent spin filtering in connection with magnetoresitance, see J. C. Egues, C. Gould, G. Richter, and L. W. Molenkamp, Phys. Rev. B 64, 195319 (2001)

[8]F. G. Brito, J. F. Estanislau, and J. C. Egues J. Magn. Magn. Mater. 226-230, 457 (2001).

[9]R. Landauer, Nature 392, 658 (1998).

[10]Ya. M. Blanter and M. Büttiker, Phys. Rep. 336, 1 (2000).

[11]J. C. Egues and J. W. Wilkins, Phys. Rev. B 58, R16012 (1998).

[12]J. C. Egues, S. Hershfield, and J. W. Wilkins, Phys. Rev. B 49, 13517 (1994).

[13]A detailed account of our calculation, along with expressions for the relevant quantities will be published elsewhere (F. G. Brito and J. C. Egues, in preparation).

Publication Dates

• Publication in this collection
  26 Nov 2002
• Date of issue
  June 2002

History

• Received
  23 Apr 2001