Abstract
In this paper, we consider a Cauchy problem for the Helmholtz equation at fixed frequency, especially we give the optimal error bound for the ill-posed problem. Within the framework of general regularization theory, we present some spectral regularization methods and a modified Tikhonov regularization method to stabilize the problem. Moreover, Hölder-type stability error estimates are proved for these regularization methods. According to the regularization theory, the error estimates are order optimal. Some numerical results are reported.
inverse problems; Helmholtz equation; spectral regularization; Tikhonov regularization; error estimate
Two approximate methods of a Cauchy problem for the Helmholtz equation
Xiang-Tuan Xiong; Chu-Li Fu
School of Mathematics and Statistics, Lanzhou University, Lanzhou 730000, P.R. China, E-mail: fuchuli@lzu.edu.cn
ABSTRACT
In this paper, we consider a Cauchy problem for the Helmholtz equation at fixed frequency, especially we give the optimal error bound for the ill-posed problem. Within the framework of general regularization theory, we present some spectral regularization methods and a modified Tikhonov regularization method to stabilize the problem. Moreover, Hölder-type stability error estimates are proved for these regularization methods. According to the regularization theory, the error estimates are order optimal. Some numerical results are reported.
Mathematical subject classification: 35R25, 35R30.
Key words: inverse problems, Helmholtz equation, spectral regularization, Tikhonov regularization, error estimate.
1 Introduction
The Cauchy problem for Helmholtz equation arises from inverse scattering problems. Specific backgrounds can be seen in the existing literature, we can refer to [1]-[6] etc. A number of numerical methods for stabilizing this problem are developed. Several boundary element methods combined with iterative, conjugate gradient, Tikhonov regularization and singular value decomposition method are compared in [6]. However, these numerical methods are short of stability analysis and error analysis. Recently, in [5] many applications for a model of Helmholtz equation are introduced, a Fourier regularization method [7] (also is known as a method by cutting off high frequency directly) is applied for solving a Cauchy problem for Helmholtz equation, some error estimates are also obtained. In [8], for sideways heat equation we connect the Fourier regularization method with general regularization theory, we discover that Fourier regularization method can be considered as the 'generalized' TSVD method [9]. Based on some ideas of [8], in this paper, we use some spectral methods [10] to solve the Cauchy problem. In addition, a revised Tikhonov regularization method is also considered. Since the numerical implementation for our methods is similar to the method provided by [5], we only give some numerical results.
This aim of this paper is to give some regularization methods within the framework of general regularization theory, which are different from "Approximate solution of a Cauchy problem for the Helmholtz equation" by T. Reginska and K. Reginski [5], where Fourier regularization method is only an 'isolated' method. Moreover, we find that for the Cauchy problem Fourier regularization method is one of the considered spectral methods.
2 Model problem and optimal error bound
Let W =
2 × (0, d) Ì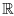 3. The first two variable are denoted by r = (x, y). In addition, there are two boundaries: G0 = {(r,0), r Î
3. The first two variable are denoted by r = (x, y). In addition, there are two boundaries: G0 = {(r,0), r Î 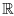 2} Ì ¶W, G = {(r, d), r Î
2} Ì ¶W, G = {(r, d), r Î 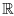 2} Ì ¶W. Let us consider the following problem for Helmholtz equation
2} Ì ¶W. Let us consider the following problem for Helmholtz equation
where Du = (¶2u)/(¶x2) + (¶2u)/(¶y2) + (¶2u)/(¶z2) and k > 0 is the wavenumber(real constant). We want to obtain the solution u(r, z) for 0 < z < d. Since the data g(·) are based on (physical) observations and are not known with complete accuracy, we assume that g(·) and gd(·) satisfy
where g(·) and gd(·) belong to L2(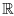 2), gd(·) denotes the measured data and d denotes the noise level, ||·|| denotes the L2(
2), gd(·) denotes the measured data and d denotes the noise level, ||·|| denotes the L2(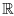 2)-norm.
2)-norm.
In order to use Fourier transform technique with respect to variable r Î 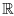 2, we define the Fourier transform
2, we define the Fourier transform
The problem (2.1) can be reformulated in the frequency space as
If u is the solution of (2.1), then its Fourier transform û is the solution to problem (2.4) and is given by
where x = (x1, x2), |x|2 =  +
+  .
.
From (2.5) and Parseval identity, we will see that if  (x) decays rapidly at |x|® ¥ in frequency domain, then the solution of problem (2.1) lies in L2(W).
(x) decays rapidly at |x|® ¥ in frequency domain, then the solution of problem (2.1) lies in L2(W).
If |x| < k, then |x|2 - k2 < 0, cosh((d - z) ) = cos((d - z)
) = cos((d - z) ). Thus, (2.5) becomes
). Thus, (2.5) becomes
If |x| > k, then |x|2 - k2 > 0, it is easy to see that if
then
Obviously cosh((d - z) ) ® ¥ as |x| ® ¥, this factor can amplify the error d arbitrarily.
) ® ¥ as |x| ® ¥, this factor can amplify the error d arbitrarily.
In (2.5), setting z = 0, we have
As usual, in order to obtain convergence rate, we assume that there exists an a-priori bound for problem (2.1):
where E is a given constant, throughout this paper, we use the same notation E.
Due to ill-posedness, problem (2.1) is unstable in numerical simulation and requires regularization methods. What is the optimal error bound for solving problem (2.1) by all regularization methods? In order to answer this question, we review some results on optimality theory for ill-posed problems.
Consider an ill-posed inverse operator equation [9], [11], [12], [13]
where A : X ® Y is a bounded linear operator between infinite-dimensional Hilbert spaces X and Y. Let ydÎ Y be the available noisy data with ||yd - y|| < d. Any operator Â: Y ® X can be seen as a special method for solving (2.9), the approximate solution to (2.9) is then given by Âyd.
Let M Î X a bounded set. Define the worst case error according to
The worst case error characterizes the maximal error of the method  if the solution x of (2.9) varies in the set M. A method Â0 is called
(i) optimal on the set M if D(d, Â0) = inf : Y ® X D(d, Â);
(ii) order optimal on the set M if D(d, Â0) < c inf : Y ® XD(d, Â) with c > 1.
Let the "source set" M be given by
where the operator function j(A* A) is well defined via spectral representation j(A* A) =  j(l)d El where A* A =
j(l)d El where A* A =  ld El is the spectral decomposition of A* A, {El} denotes the spectral family of the operator A* A and a is a constant with ||A* A|| < a. In addition,
ld El is the spectral decomposition of A* A, {El} denotes the spectral family of the operator A* A and a is a constant with ||A* A|| < a. In addition,
Assumption 2.1. The function j : (0,a] ® (0,¥) in (2.11) is continuous and satisfies
(i) liml ® 0 j(l) = 0
(ii) j(l) is strong monotonically increasing on (0,a]
(iii) r(l) = lj-1(l) : (0, j(a)] ® (0, aj(a)] is convex.
Theorem 2.2. [12] Let M be given by (2.11), let Assumption 2.1 be satisfied and d2/(E2) Î s(A* Aj(A* A)) where s(A* A) denotes the spectrum of the operator A* A. Then
Based on Theorem 2.2, we can obtain the following results:
Theorem 2.3. Let d2/E2< 1. Then under the assumption (2.8) we have the following optimal error bound for problem (2.1)
As for the proof of Theorem 2.3, we can refer to the Appendix Appendix .
Most regularization operators can be written in the form,
with some function ga satisfying
where a > 0 plays the role of regularization parameter. Then for the regularization solution with noisy data, we have  : = Âa yd. For example,
: = Âa yd. For example,
Spectral method 1.
Spectral method 2.
Spectral method 3 (TSVD method).
Tikhonov method.
In general, the exact solution xÎ X is required to satisfy a so-called source condition, otherwise the convergence of the regularization method approximating the problem can be arbitrarily slow. For problem (2.1), the condition (2.8) is assumed for the above reason.
3 Error estimates on the Cauchy problem for the Helmholtz equation
In this section, we will analyze the error estimates by different regularization methods.
By the similar method in [14], (2.1) can be formulated as an operator equation in frequency domain
obviously, the multiplication operator Â(z) is given by
and
Now we give a new interpretation for the Fourier regularization method provided by [5]. Applying the TSVD method for solving problem (2.1), we have
The inequality  < a is equivalent to
< a is equivalent to
If |x| > k, the (3.4) is equivalent to
Obviously, regularization method (3.3) stabilize problem (2.1) by cutting off high frequency.
If the spectral method 1 is devoted to solving problem (2.1), then we get
Because the three spectral methods in Section 2 are very similar, we only give the approximation properties of the first spectral method.
Theorem 3.1. Supposed that u(r, z) is exact solution with exact data g and that
(r, z) is approximate solution by spectral method 1 with noisy data gd. If we have an a-priori bound ||u(·, 0)|| < E and the data functions satisfy ||g - gd||< d, and if we choose
then we can obtain the following error estimate for d ® 0:
Proof. For the subsequent analysis, we define two sets: W: = {x : |x| < k} and I: = {x : |x| > k}. Due to Parseval identity, we have
According to
2 = W È I, there holds
Case I: |x|2 - k2 > 0, i.e., x Î I.
First define two sets
and
due to the inequality
<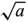 +
+ 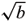 , fora a, b > 0, we have
, fora a, b > 0, we have
where
For I1, by noting the definition of the set A, we obtain
For I2, according to the triangle inequality
||a - c + c - b|| < ||a - c|| + ||b - c||
and the formula (2.7), we have
where
Noting that the set B is equivalent to {h | 1/ cosh((d - z)h) <  }, where h :=
}, where h :=  , we have
, we have
As for I4, via the formula (2.8), there holds
It is easy to see that the elements in the set B satisfy
1 - a| cosh((d - z)  |2 < 0.
|2 < 0.
So by neglecting the negative term -  , we have
, we have
On the one hand f(h): = cosh((d - z)h)/ cosh(dh) is decreasing with respect to h for 0 < z < d, on the other hand, the set B is equivalent to
hence
According to the selection (3.6) of a, cosh ( arccosh (
arccosh ( )) = E/d holds. Thus
)) = E/d holds. Thus
Combination of (3.12) and (3.16) gives
Hence by (3.9) (3.10) and (3.17), we get
According to the asymptotic expression d cosh (t arccosh  ) = Et(
) = Et( )1-t (1+o(1)), for d ® 0, 0 < t < 1 in [14], we have
)1-t (1+o(1)), for d ® 0, 0 < t < 1 in [14], we have
Case II: |x|2 - k2< 0, i.e., x Î W.
In this case, we note that cosh((d - z) ) = cos((d - z)
) = cos((d - z) ). It is easy to establish the following error estimate
). It is easy to establish the following error estimate
Therefore, via (3.8), (3.19), (3.20), we get the error estimate (3.7).
Remark 3.2. For the other two spectral methods, if the regularization parameter a is properly chosen, we can establish the error estimates similarly. We formulate it as follows:
where C is a positive constant without depending on d and E. From the theory of Section 2, we can conclude that these three spectral regularization methods are order optimal.
Now we will devote to the Tikhonov regularization method. According to Section 2, similarly we have the following regularized solution in the frequency domain:
If the 1 + a| cosh((d - z) )|2 is replaced by a faster filter 1 + a|cosh((d)
)|2 is replaced by a faster filter 1 + a|cosh((d) )|2, we have the revised Tikhonov approximate solution [15, 16]
)|2, we have the revised Tikhonov approximate solution [15, 16]
Lemma 3.3. Let 0 < z < d, |x| > k, a > 0. Then
Proof. First we prove (3.24). Let h: =  and note that cosh((d - z)h) < exp((d - z)h), we have
and note that cosh((d - z)h) < exp((d - z)h), we have
Denote z(h): =  . Differentiating z and setting z¢ (h0) = 0, we find
. Differentiating z and setting z¢ (h0) = 0, we find
moreover, for
h > h0, z¢ (h) < 0; for h < h0, z¢ (h) >0,
hence z(h) attains its unique maximum zmax = z(h0) at the point h0. Since (3.27),
So
Due to (3.26), we have
< z(h) < z(h0).Noting (3.28), we have the inequality (3.24).
As for (3.25), noting cosh(dh) < exp(dh) and (3.26), we obtain
Repeating the process in the case of (3.24) for b(h) yields the inequality(3.25).
Theorem 3.4. Supposed that u(r, z) is exact solution with exact data g and that
, RTik(r, z) is approximate solution by revised Tikhonov method with noisy data gd. If we have an a-priori bound ||u(·, 0)|| < E and the data functions satisfy ||g - gd|| < d, and if we choose a = (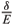 )2, then we can obtain the following error estimate for d ® 0:
)2, then we can obtain the following error estimate for d ® 0:
Proof. Due to Parseval identity, we have
Similar to the proof of Theorem 3.1, there holds
Case I: |x|2 - k2 > 0, i.e., x Î I.
In this case, noting the inequalities (3.24) and (3.25), we have
Thus we take
a = (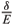 )2.
)2.
Hence we have
Case II: |x|2 - k2< 0, i.e., x Î W.
In this case, we have
Thus, according to (3,31), (3.33), (3.34), it yields (3.30).
4 Numerical experiments
In this section, some numerical results are reported in order to show how the regularization method works. In section 3, we have seen that the Fourier regularization method in [5] is also the Spectral method 3 (TSVD). Since some numerical results on Fourier regularization method has been investigated, here we only provide numerical results for the revised Tikhonov regularization method. For sake of comparison, we take the same numerical example as the one in [5]. The numerical experiments are accomplished by Matlab.
In our test problem d = 1 and k = 4 are fixed. We take the function
as an exact data function on G := (-p, p)2. For creating gd, a normally distributed noise of variance e is added to g. A matrix Gd containing samples from gd on an equidistant grid  for n = 64 is created firstly. Using the 2D fast Fourier transform (FFT2) to the matrix Gd, we can obtain a new matrix approximating the Fourier transform of gd. Next, this new matrix is multiplied by the matrix
for n = 64 is created firstly. Using the 2D fast Fourier transform (FFT2) to the matrix Gd, we can obtain a new matrix approximating the Fourier transform of gd. Next, this new matrix is multiplied by the matrix
finally the 2D inverse FFT (IFFT2) is applied. The results are shown as follows:
From the above results, we can see that the revised Tikhonov regularization works well. Furthermore from Fig. 1 to Fig. 2, from Fig. 3 to Fig. 4, we find that the regularization parameter a cannot be too small. Certainly a can not be too large. This accords with the regularization theory.
5 Concluding remark
In this paper, we obtained order optimal error estimates by spectral regularization methods and a revised Tikhonov regularization method for a Cauchy problem for the Helmeholtz equation. The Fourier regularization method in [5] can be considered as the spectral method 3 (TSVD). Numerical results show that the methods work well.
Acknowledgements. The authors would like to thank the referees for their carefully reading and valuable comments and suggestions on the manuscript, which led to an improvement version. The work is supported by the National Natural Science Foundation of China (Nos. 10671085, 10571079), the Natural Science Foundation of Gansu Province of China (No. 3ZS051-A25-015) and the Fundamental Research Fund for Physics and Mathematics of Lanzhou University (No. Lzu05005).
Received: 21/VII/06. Accepted: 26/III/07.
#675/06.
Appendix: proof of theorem 2.3
In order to prove the Theorem 2.3, we formulate the problem of identifying u(r, z) from (unperturbed) data g(r) as an operator equation
with a linear operator A(z) Î L2( 2) ® L2(
2) ® L2( 2). Equation (A.1) is equivalent to the operator equation
2). Equation (A.1) is equivalent to the operator equation
where F : L2(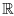 ) ® L2(
) ® L2(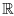 ) is the Fourier operator. From (2.5), the multiplication operator Â(z) is given by
) is the Fourier operator. From (2.5), the multiplication operator Â(z) is given by
i.e.,
with
Thus,
Obviously, Â-1(z) is an unbounded multiplication operator in that cosh((d - z)h) ® ¥ as h ® ¥. Hence we can call the the set I: = {x | |x| > k} is the ill-posed part of problem (A.2). For treating the ill-posed part, we need to transform the source condition (2.8) into an equivalent condition in the frequency. First the condition (2.8) is equivalent to
Proposition A.1.Consider the operator equation (A.2). Then the set M given by (A.7) is equivalent to the general source set
where j(l) is given by (in parameter representation)
where 1 < h < ¥.
Proof. Noting that (A.7) and (A.8), we can obtain (A.9) easily.
Proposition A.2.The function j(l) given by (A.9) is continuous and satisfies the properties:
(i) liml ® 0 j(l) = 0;
(ii) j(l) is strong monotonically increasing;
(iii) r(l) = lj-1(l) is strong monotonically and possesses the parameter representation
(iv) r-1(l) is strong monotonically increasing and possesses the parameter representation
(v) for the inverse function r-1of r there holds for any fixed z Î (0, d)
Proof. Consider l(h) given by (A.9), we have
We can see that l(h) is strong monotonically decreasing with limh ® ¥ l(h) = 0. So,
 j(l) =
j(l) = 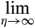 cosh2 ((d - z)h)/ cosh2 (dh) = 0, for d > z.
cosh2 ((d - z)h)/ cosh2 (dh) = 0, for d > z.
Thus conclusion (i) holds. Noting that the function f(x) = x tanh(x) is a strong monotonically increasing, we have
From (A.13) and (A.14), it is easy to see j¢(l) =  > 0. Thus, we proved (ii). Obviously j-1(l) is strong monotonically increasing, consequently, r(l) is strong monotonically increasing. (A.10) can be obtained by
> 0. Thus, we proved (ii). Obviously j-1(l) is strong monotonically increasing, consequently, r(l) is strong monotonically increasing. (A.10) can be obtained by
l(h) = cosh2 ((d - z)h) / cosh2 (dh), j-1 (h) = 1/(cosh2 ((d - z)h)).
Now (iv) is a direct conclusion of (iii). In order to prove (v), we need to prove that liml ® 0 F(l) = 1 where F(l) is given by
F(l) = r-1 (l)(1/l)z/d.
We use (A.11), note that l(h) is strong monotonically decreasing with limh ® ¥ l(h) = 0, we have
F(l) =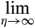 [cosh2 ((d - z)h)/ cosh2 (dh)] (cosh2 (dh))z/d = 1.
[cosh2 ((d - z)h)/ cosh2 (dh)] (cosh2 (dh))z/d = 1.
Thus, we proved (v).
Proposition A.3. The function r(l) given by (A.10) is strong convex.
Proof. From r" =  and
and  < 0 we get that r" > 0 is equivalent to
< 0 we get that r" > 0 is equivalent to 
 <
< 
 . Noting that l(h) = r(h)f(h) with f(h) = cosh2((d - z)h), hence r" > 0 is equivalent to the inequality
. Noting that l(h) = r(h)f(h) with f(h) = cosh2((d - z)h), hence r" > 0 is equivalent to the inequality
Let x = dh and t = (d - z)/d, by elementary calculations we find that (A.15) is equivalent to the inequality
where
Since h(x) = x coth(2x) is strong monotonically increasing on 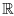 +, we find that y(x) > 0 holds for any x > 0 and 0 < t < 1. Hence (A.15) always holds, i.e., r is strong convex.
+, we find that y(x) > 0 holds for any x > 0 and 0 < t < 1. Hence (A.15) always holds, i.e., r is strong convex.
Now we apply Theorem 2.1 to our problem in the frequency domain. According to Proposition A.1-Proposition A.3, the conditions in Assumption 2.1 are satisfied for the operator Â(z). Due to (A.9),
s(Â* Âj(Â*Â)) = s(1/ cosh2 (dh)) = (0,1]
holds. If d2/E2< 1, then obviously d2/E2Î s(Â* Âj(Â*Â)) holds. Noting
where the supremum is taken over gd(r) Î L2(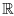 2),
2),  < d and u(r, z) Î M, we define
< d and u(r, z) Î M, we define
where the supremum is taken over
d(x) Î L2(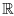 2),
2), 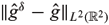 < d and û(x, z) Î
< d and û(x, z) Î 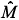 . According to Parseval identity, we have w(d, Â) =
. According to Parseval identity, we have w(d, Â) = 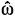 (d,
(d, 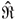 ). Moreover, according to the definition of
). Moreover, according to the definition of 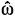 (d,
(d, 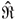 ),
), 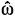 (d,
(d, 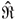 ) =
) = 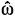 I(d,
I(d, 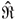 ) +
) + 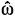 W(d,
W(d, 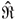 ), where
), where 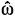 I(d,
I(d, 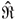 ) and
) and 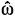 W(d,
W(d, 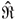 ) denotes the optimal error boundson the sets I and W, repectively.
) denotes the optimal error boundson the sets I and W, repectively.
For I Ì 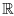 2, the best possible error bound in the frequency domain
2, the best possible error bound in the frequency domain
For W Ì 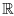 2, a regularized multiplication operator satisfies ||
2, a regularized multiplication operator satisfies ||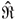 || < c where c is a constant depending on regularization parameter. Moreover, there holds
|| < c where c is a constant depending on regularization parameter. Moreover, there holds
but
from Section 3, for spectral cut-off method, the error estimates for  and
and  is d and 0, respectively. Hence in W the best possible error bound
is d and 0, respectively. Hence in W the best possible error bound 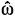 W(d,
W(d, 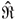 ) = d.
) = d.
Obviously d = o( ), for d ® 0, hence we obtain Theorem 2.3.
), for d ® 0, hence we obtain Theorem 2.3.
- [1] A. Kirsch, An Introduction to the Mathematical Theory of Inverse Problems, New York: Springer-Verlag, 1996.
- [2] I. Harari, P.E. Barbone, M. Slavutin and R. Shalom, Boundary infinite elements for the Helmholtz equation in exterior domains. International Journal for Numerical Methods in Engineering, 41 (1998), 1105-1131.
- [3] L. Marin, L. Elliott, P.J. Heggs, D.B. Ingham, D. Lesnic and X. Wen, An alternating iterative algorithm for the Cauchy problem associated to the Helmholtz equation. Computer Methods in Applied Mechanics and Engineering, 192 (2003), 709-722.
- [4] L. Marin, L. Elliott, P.J. Heggs, D.B. Ingham, D. Lesnic and X. Wen, Conjugate gradient-boundary element solution to the Cauchy problem for Helmholtz-type equations. Computational Mechanics, 31 (2003), 367-377.
- [5] T. Reginska and K. Reginski, Approximate solution of a Cauchy problem for the Helmholtz equation. Inverse Problems, 22 (2006), 975-989.
- [6] L. Marin, L. Elliott, P.J. Heggs, D.B. Ingham, D. Lesnic and X. Wen, Comparison of regularization methods for solving the Cauchy problem associated with the Helmholtz equation. Int. J. Numer. Meth. Engng., 60 (2004), 1933-1947.
- [7] L. Eldén, F. Berntsson and T. Reginska, Wavelets and Fourier methods for solving the sideways heat equation. SIAM J. Sci. Comput., 21 (2000), 2187-2205.
- [8] Xiang-Tuan Xiong, Chu-Li Fu and Hong-Fang Li, Fourier regularization method of a sideways heat equation for determining surface heat flux. J. Math. Anal. Appl., 317 (2006), 331-348.
- [9] H.W. Engl, M. Hanke and A. Neubauer, Regularization of Inverse Problems, Kluwer Academic Publisher, Dordrecht Boston London, 1996.
- [10] U. Tautenhahn Optimal stable approximations for the sideways heat equation. J. Inv. Ill-Posed Problems, 5 (1997), 287-307.
- [11] T. Hohage, Regularization of exponentially ill-posed problems. Numer. Funct. Anal. Optim., 21 (2000), 439-464.
- [12] U. Tautenhahn, Optimality for linear ill-posed problems under general source conditions. Numer. Funct. Anal. Optim., 19 (1998), 377-398.
- [13] P. Mathé and S. Pereverzev, Geometry of ill-posed problems in variable Hilbert Scales. Inverse Problems, 19 (2003), 789-803.
- [14] U. Tautenhahn, Optimal stable solution of Cauchy problems of elliptic equations. J. Analysis and its Applications, 15(4) (1996), 961-984.
- [15] A. Carasso, Determining surface temperature from interior observations. SIAM J. Appl. Math., 42 (1982), 558-574.
- [16] C.L. Fu, Simplified Tikhonov and Fourier regularization methods on a general sideways parabolic equation. J. Comput. Appl. Math., 167 (2004), 449-463.
Appendix
Publication Dates
-
Publication in this collection
24 July 2007 -
Date of issue
2007
History
-
Accepted
26 Mar 2007 -
Received
21 July 2006
































































































