Abstract
We show that the solutions of a thermoelastic system with a localized nonlinear distributed damping decay locally with an algebraic rate to zero, that is, given an arbitrary R > 0, the total energy E(t) satisfies for t > 0: E(t) < C (1 + t)-γ for regular initial data such that E(0) < R, where C and γ are positive constants. In the two-dimensional case, we obtain an exponential decay rate when the nonlinear dissipation behaves linearly close to the origin.
thermoelastic system; nonlinear localized damping; algebraic decay rate; exponential decay rate
Stabilization of a locally damped thermoelastic system
Jáuber C. Oliveira* * Corresponding author. ; Ruy C. Charão
Departamento de Matemática, Universidade Federal de Santa Catarina 88040-900 Florianópolis, SC, Brasil E-mails: jauber@mtm.ufsc.br, charao@mtm.ufsc.br
ABSTRACT
We show that the solutions of a thermoelastic system with a localized nonlinear distributed damping decay locally with an algebraic rate to zero, that is, given an arbitrary R > 0, the total energy E(t) satisfies for t > 0: E(t) < C (1 + t)γ for regular initial data such that E(0) < R, where C and γ are positive constants. In the two-dimensional case, we obtain an exponential decay rate when the nonlinear dissipation behaves linearly close to the origin.
Mathematical subject classification: 35B40, 35L70.
Key words: thermoelastic system, nonlinear localized damping, algebraic decay rate, exponential decay rate.
1 Introduction
In this work we study decay properties of the solutions of the following initial boundary-value problem associated with the thermoelastic system:
where Ω is a bounded domain in
N, N > 2. u(x, t) = (u1 (x, t), ..., uN (x, t)) is the vector displacement, Δ u = (Δ u1 (x, t), ..., Δ uN (x, t)) is the Laplacian operator of u, div u is the divergence of u and ∇ is the gradient operator. θ represents the temperature distribution. The vector function ρ is a dissipative term, localized in a neighborhood of part of the boundary of Ω. The coefficients a and b are related to the Lamé coefficients of Elasticity Theory and b2 > a2 > 0.In this paper, we show the uniform stabilization of the total energy for the system (1.1)-(1.4) with algebraic rates, where the dissipative term ρ(x, ut) is strongly nonlinear and effective only in a neighborhood of part of the boundary. When the nonlinear dissipative term ρ(x, s) behaves linearly for small s and the dimension is two, we obtain an exponential decay rate for the total energy of the system. If the dimension N > 3 and ρ(x, s) behaves linearly for all s, then the decay rate is also exponential. To prove these results we use ideas of [10], [8] and [13] to obtain some energy identities associated with localized multipliers in order to construct special difference inequalities for the associated energy. The main estimates in this work are obtained using Holmgren's Uniqueness Theorem and Nakao's Lemma.
Regarding works on the stabilization of thermoelastic systems, Dafermos [2] investigated the existence, uniqueness, regularity and stabilization (without rates) of the solution for the linear system in one dimension. Racke [17] considered a Cauchy problem for the three-dimensional nonlinear thermoelasticity equations and proved the global existence of smooth solutions for sufficiently small and smooth initial data. It was necessary to assume that certain nonlinear terms are quasilinear and have cubic nonlinearity.
Pereira-Perla Menzala [15] proved that the total energy of the linear thermoelastic system in an isotropic, non-homogeneous (bounded, n-dimensional) medium, with a linear dissipative term effective in the whole domain, decays to zero in an exponential rate. Rivera [23] later proved that the energy of the classical one-dimensional thermoelastic system decays to zero exponentially. Also, Henry-Lopes-Perisinotto [5] showed, using spectral analysis, that the three parts of the energy of that system decay exponentially to zero in the one-dimensional case, but such decay does not occur in higher dimensions.
Racke [18] used the energy method to prove the exponential decay to zero of displacement and temperature for the three-dimensional equations of linear thermoelasticity in bounded domains for inhomogeneous and anisotropic media assuming a linear damping force. Racke-Shibata-Zheng [20] considered the Dirichlet initial-boundary value problem in one-dimensional nonlinear thermoelasticity to prove that if the initial data are closed to the equilibrium then the problem admits a unique global smooth solution. They proved that as time tends to infinity, the solution is exponentially stable. They also used techniques based on the work of Rivera [23] to improve previous results of Racke-Shibata [19], which were based on spectral analysis to obtain decay rates for solutions of nonlinear thermoelasticity in one dimension. Rivera-Barreto [24] improved further the global in time unique existence result with exponential decay of the energy obtained by Racke-Shibata-Zheng [20] by assuming more general smoothness hypothesis on the initial data.
Rivera [22] considered the linear, inhomogeneous thermoelasticity equations in one dimension for a bounded domain with several boundary conditions considered. It is proved that the solution (u, θ) has some partial derivatives decaying exponentially to zero in the L2-norm. Rivera [21] investigated the linear homogeneous and isotropic thermoelasticity equations with homogeneous Dirichlet boundary conditions in a general n-dimensional domain. The author shows that the curl-free part of the displacement and the thermal difference decay exponentially to zero as times goes to infinity. It is also proved that the divergence-free part of the displacement conserves its energy, which implies that if the divergence-free part of the initial data is not zero, then the total energy does not decay to zero uniformly.
Jiang, Rivera and Racke [7] proved the exponential decay for solutions of the linear isotropic system of thermoelasticity in bounded two- or three-dimensional domains with the hypothesis that the rotation of the displacement vanishes.
Lebeau-Zuazua [9] studied the linear system of thermoelasticity in two- and three-dimensional smooth bounded domain. They analyzed whether the energy of solutions decays exponentially to zero. They also prove that when the domain is convex, the decay rate is never uniform. Liu-Zuazua [12] established explicit formulas for the decay rate of the energy of a body in the framework of linear thermoelasticity when some part of the boundary of the body is clamped and on the rest there is some nonlinear velocity feedback. This result was obtained using the theory of semigroups, Lyapunov methods and multiplier techniques. Qin and Rivera ([16]) established the global existence, uniqueness and exponential stability of solutions to equations of one-dimensional nonlinear thermoelasticity with relaxation kernel and subject to Dirichlet boundary conditions for the displacement and to Neumann boundary conditions for the temperature difference.
Irmscher-Racke [6] obtained explicit sharp decay rates for solutions of the system of classical thermoelasticity in one dimension. They also considered the model of thermoelasticity with second sound and compared the results of both models with respect to the asymptotic behavior of solutions.
Our work generalizes, in the context of pure elasticity, the previous work of Bisognin-Bisognin-Charão ([1]), where it is proved a stabilization theorem with polynomial decay rate for the total energy of the system only in three-dimensions. We should mention that the work of Bisognin-Bisognin-Charão ([1]) generalized the work of Guesmia ([3]) that proved the stabilization of the total energy for pure system of elasticity with a nonlinear localized dissipation which does not couple the system of equations and behaves linearly far from the origin. Our work also generalizes the previously mentioned work of Pereira-Perla Menzala ([15]). Regarding the work of Jiang-Rivera-Racke ([7]), instead of assuming their condition that the rotation of the displacement vanishes and the dimension is two or three, we consider in the system a nonlinear localized weak dissipation in any dimension N > 2. Furthermore, according to the previous mentioned works, only part of the energy of the free thermoelastic system decays uniformly if N > 2. Thus, in this sense, our work also improves those results and other previous results for the thermoelastic system due to the fact that we have obtained exponential decay for the total energy when N = 2 and polynomial decay rate when N > 3 by including a weak localized nonlinear dissipative term ρ(x, s) in the system.
2 Hypotheses and Notation
Throughout this work the dot ( ∙ ) will represent the usual inner product betweentwo vectors in
N. Let V1 =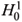 (Ω)N, V2 =
(Ω)N, V2 = 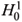 (Ω), U1 = V1∩ H2 (Ω)N, U2 = V2∩ H2 (Ω). || denotes the norm of a vector in
(Ω), U1 = V1∩ H2 (Ω)N, U2 = V2∩ H2 (Ω). || denotes the norm of a vector in 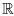 N, |∇u(x, t)|2 =
N, |∇u(x, t)|2 = 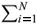 |∇ui(x, t)|2, ( , ) represents the inner product in L2(Ω)N and || || denotes the corresponding norm. Also, ||∇u||2 =
|∇ui(x, t)|2, ( , ) represents the inner product in L2(Ω)N and || || denotes the corresponding norm. Also, ||∇u||2 = 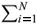 ||∇ui||2 and
||∇ui||2 and 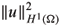 =
= 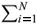
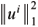 , where || ||1 denotes the usual norm in H1(Ω). We use |Ω| to represent the measure of Ω.
, where || ||1 denotes the usual norm in H1(Ω). We use |Ω| to represent the measure of Ω.
Now, we list the hypotheses which we use to establish existence and uniqueness of solutions.
(H0) Ω ⊂
N is a bounded open set with smooth boundary (at least of class C2);(H1) uoЄ U1, u1Є V1; θoЄ U2
(H2) ρ:
×
N→
N is a function such that:
(a) ρ(x, s) ∙ s > 0, s Є
N, x Є
;
(b) ρ and
are continuous functions in
×
N;
(c)
uk > 0, ∀u Єui
N, ∀x Є
, ∀s Є
N, i.e.,
is positive semi-definite.
(d) There exist positive constants K0, K1, K2 and K3 and numbers p, r, -1 < r < +∞, -1 < p <
if N > 3 and -1 < p < +∞ if N = 1 or 2, such that: K2a(x) |s|r+2< ρ(x, s) ∙ s and |ρ(x, s)| < K0a(x) (|s|r+1 + |s|), for |s| < 1, K3a(x) |s|p+2< ρ(x, s) ∙ s and |ρ(x, s)| < K1a(x)(|s|p+1 + |s|), for |s| > 1, where the function a = a(x) is such that a:
→
+ belongs to L∞ (Ω).
Remark 1. If a(x) is a continuous function on  , then ρ(x, s) = a(x)|s|ps, s Є
, then ρ(x, s) = a(x)|s|ps, s Є 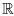 N, is an example of a function which satisfies (a)-(d) with r = p.
N, is an example of a function which satisfies (a)-(d) with r = p.
In order to study the stabilization of the total energy for this system, we specify where the damping is effective in the domain, that is, where the dissipative term is localized. We choose xo in 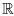 N and we define
N and we define
Γ (xo) = {x Є ∂ Ω: (x - xo) ∙ η(x) > 0},
where η(x) denotes the outward unit normal vector at x Є ∂Ω.
Now, let ω ⊂  be a neighborhood of Γ (xo). Then, in addition to the hypothesis (H2)(d) that the function a = a(x) is nonnegative, we also assume that
be a neighborhood of Γ (xo). Then, in addition to the hypothesis (H2)(d) that the function a = a(x) is nonnegative, we also assume that
a(x) >ao > 0 , in ω.
The energy E(t) of the system (1.1) is defined by
where {u = u(x, t), θ = θ(x, t)} is the solution of (1.1)-(1.4). We denote the energy difference E(t) - E(t + T) by ΔE. Also, let E1 denote the part of E without the term 1/2 ∫Ωθ2, and E2 = E - E1.
In order to reduce the size of the formulas, we use the following notation.
Remark 2. The multiplication of (1.1) by ut, (1.2) by θ followed by adding the resulting equations and integrating over Q (t) produces:
The hypothesis H2(a) implies that the energy is a nonincreasing functionof t.
3 Results
Regarding the existence and uniqueness of solution for the problem (1.1)-(1.4), the following result holds.
Theorem 3.1 (Existence and Uniqueness). Under the hypotheses of the previous section, the initial-boundary value problem (1.1)-(1.4) has a unique solution u = u(x, t), θ = θ(x, t) such that for each T > 0, u Є C([0, T], U1), utЄ C([0, T], V1), uttЄ C([0, T], L2(W)N), Є θ C([0,T], U2) and θ' Є C([0,T], V2).
Proof. We sketch the proof based on Semigroups for the nonlinear case. We consider the operator A defined by
where A1u = -a2Δ u - (b2 - a2) ∇ div u, A2θ = -Δθ, B θ = -∇θ, and C v = -div v. The domain of A : D(A) ⊂ H → H is given by
U1 × V1 × U2,
where
H = V1 × L2(Ω)N × L2(Ω)
is a Hilbert space with the inner product
〈(z1, z2, z3),(w1, w2, w3)〉 = ∫Ω{z2w2 + a2
+ (b2 - a2) div (w1) div (z1) + z3w3} dx.
Then, the original problem is equivalent to
where
F (w1, w2, w3) = (0, ρ(∙, w2), 0)
We use the theorem of Hille-Yosida to prove that the operator A (densely defined) generates a Cº-semigroup of contractions. The hypotheses of the Hille-Yosida are verified after proving that for each positive λ, there exists (λI - A)-1Є  (H) and ||(λI - A)-1 || <
(H) and ||(λI - A)-1 || <  .
.
Next, using hypothesis H2(b), it is easy to prove that F : H → H is Lipschitz continuous on bounded sets. As a consequence, one obtains a local (generalized) solution on a interval [0, Tmax]. Then, by proving that ||U||X< C E(0), where is used the fact that the total energy of the system is decreasing due to hypothesis (H2)(a), it is possible to show that the solution can be extended to the interval [0, ∞). Finally, by using hypothesis (H2)(b), one proves that F is continuously differentiable. It follows that the generalized solution of (3.2)-(3.3) is a classical solution on [0, ∞). The uniqueness follows from the hypothesis (H2)(c) on the function ρ.
□
3.1 Boundedness of the Laplacian L 2 -norm
In the previous section, we proved the existence of a unique solution (u, θ) for the thermoelastic system in the class
u Є C ([0, ∞); H2(Ω)N∩ 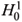 (Ω)N) ∩ C1 ([0, ∞);
(Ω)N) ∩ C1 ([0, ∞); 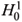 (Ω)N) ∩ C2 ([0, ∞); L2 (Ω)N)
(Ω)N) ∩ C2 ([0, ∞); L2 (Ω)N)
and
θ Є C ([0, ˞); H2(Ω) ∩ 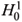 (Ω)) ∩ C1 ([0 ∞);
(Ω)) ∩ C1 ([0 ∞); 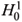 (Ω))
(Ω))
In order to prove that
we write
where Lu is the differential operator defined by
Lu = -a2Δu - (b2 - a2) ∇ div u.
To show (3.4), we only need to show that each term in the right-hand side of the equation (3.5) is in L∞ (0, ∞; L2(Ω)N). This is proved in the next Lemmas. Then, the uniform boundedness of L2-norm of the Laplacian of u follows from the elliptic regularity of the operator L.
Lemma 3.2. The L2-norm of ρ(∙, u1) is bounded by a constant that depends only on the initial data u0, u1, θ0.
Proof. We have ||ρ (x, u1)||2<  |ρ(x, u1)|2dx +
|ρ(x, u1)|2dx +  |ρ(x, u1)|2dx, where
|ρ(x, u1)|2dx, where
Ω1: = {x Є Ω : |u1| < 1}
and
Ω2 = Ω - Ω1.
If r > 0, then, due to our hypothesis on the function ρ,
which is bounded (u1Є L2(Ω)N).
Let N > 3 and 0 < p <  , then due to the hypotheses on the function ρ
, then due to the hypotheses on the function ρ
The last estimate is due to facts that 2 < 2 p + 2 <  and
and 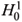 (Ω) is continuously embedded in Lq (Ω) for q Є [2,
(Ω) is continuously embedded in Lq (Ω) for q Є [2,  ]. Thus, the lemma holds for the case 1: N > 3, r > 0 and 0 < p <
]. Thus, the lemma holds for the case 1: N > 3, r > 0 and 0 < p <  .
.
The proof of the other cases is similar.
□
Now, we obtain an estimate for the L2-norm of ||utt(0)||.
Lemma 3.3. There is a positive constant C = C(u0, u1, θ0) such that ||utt(0)||< C and ||θt(0)|| < C.
Proof. We take L2 inner-product between the first equation in the thermoelastic system with utt(t) and evaluate at t = 0 to obtain
Since utt(0) Є L2(Ω)N, u0Є H2(Ω)N and θ0 Î H2(Ω), we have the following estimate
The result follows now from the previous lemma and our hypothesis on the initial data. The proof of the estimate for θ is similar.
□
Lemma 3.4.
(i) utt belongs to L∞(0, ∞; L2(Ω)N) and for each t the L2-norm of utt(t) is bounded by a constant that depends only on the initial data u0, u1, θ0.
(ii) For all t Є (0, ∞),
Proof. We differentiate once the first equation of the thermoelastic system with respect to t, multiply each member of the resulting equation by utt and integrate over Ω. Therefore, we have
By the hypothesis on the initial data (u1Є 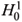 (Ω)N), it follows that a2
(Ω)N), it follows that a2 + (b2 - a2) div u1 belongs to L2(Ω)N. So, after integrating this equation over [0, t], we obtain
+ (b2 - a2) div u1 belongs to L2(Ω)N. So, after integrating this equation over [0, t], we obtain
Now, differentiating the second equation of the thermoelastic system withrespect to t, multiplying by θt and integrating over Ω, we obtain
 ||θt||2 + 2 ||∇θt||2 - 2 (∇θt, utt) = 0.
||θt||2 + 2 ||∇θt||2 - 2 (∇θt, utt) = 0.
Integrating over [0, t], we obtain
Adding equations (3.10) and (3.11) and using (H2)(c), we obtain
The result follows from the Lemma 3.3.
□
Lemma 3.5. The L2-norm of ρ(., u(t)) is bounded by a constant that depends only on the initial data u0, u1, θ0.
Proof. This proof is similar to the proof of Lemma 3.2, therefore we present the proof for the three-dimensional case only.
||ρ(x, u)||2<  |ρ(x, u)|2dx +
|ρ(x, u)|2dx +  |ρ(x, u)|2dx, where for each t,
|ρ(x, u)|2dx, where for each t,
Ω1(t) := {x Є Ω: |ut(t)| < 1}
and
Ω2(t) = Ω - Ω1(t).
Let
and
In order to prove the result, it is sufficient to estimate I1(t) considering the cases r > 0 and -1 < r < 0, and estimate I2(t) considering the cases 0 < p < 2 and -1 < p < 0. If r > 0, then, due to H2(d),
The last inequalities are due to the fact that ||ut||2 is part of the energy and the fact that the energy is decreasing.
If 0 < p < 2, then due to H2(d),
The last term in this estimate is bounded for all t due to the previous lemma.
where the last inequality follows from Hölder's inequality. If -1 < p < 0, then
Lemma 3.6. ∇ θ Є L∞ (0, ∞; L2(Ω )N).
Proof. We use the fundamental identity:
Then, due to the hypothesis H2(a), we have
However,
Therefore, using Cauchy-Schwartz's inequality, we obtain
The terms ||ut||2, ||∇u||2, ||div u||2, ||θ||2 are all bounded by a constant (independent of t) times the initial energy, since they are part of the energy and the energy is bounded by the initial energy. The remaining terms are boundeddue to Lemma 3.4. We conclude that ||∇ θ|| is bounded for all t, which concludes the proof.
□
In summary:
< C with C a positive constant which does not depend on t and depends only on the initial data, ||a(.)||∞ and |Ω|.3.2 Theorem on stabilization
From now on, we will study the asymptotic behavior of the total energy of the system. Under certain hypothesis we will obtain exponential decay of the energy, which means that there exist positive constants M0 and k0 such that E(t) < M0 exp(-k0t) if t > 0.
The main result of this paper is the following theorem of stabilization for the total energy of the system.
Theorem 3.7 (Stabilization). Let R > 0 and initial data in D(A) satisfying E(0) < R. Then, under the previous hypotheses, the total energy for the solution u = u(x, t), θ = θ (x, t) of the problem (1.1)-(1.4) has the following asymptotic behavior in time
where C = C(R, r, p) is a positive constant (which depends on the initial data, ||a||∞ and |Ω|) and the decay rate γ is given according to the following cases:
Case 1. If N = 2 and
(a) -1 < r < 0 and -1 < p < +∞ then γ =
;
(b) r > 0 and -1 < p < +∞, then γ =
.
Case 2. If N > 3 and
(a) r > 0 and 0 < p <
, then γ = min
;
If r = 0 and 0 < p <  , then γ =
, then γ =  ;
;
If r > 0 and p = 0, then γ =  ;
;
(b) r > 0 and -1 < p < 0, then γ = min
;
If r = 0 and -1 < p < 0, then γ =  ;
;
(c) -1 < r < 0 and 0 < p <
, then
If -1 < r < 0 and p = 0, then γ =  ;
;
(d) -1 < r < 0 and -1 < p < 0, then
The decay rate is exponential in the following cases:
(a) N = 2 , r = 0 and -1 < p < +¥,
(b) N > 3 and r = p = 0.
4 Energy identities
In the next lemma, we obtain energy identities that will be used in the following sections to obtain estimates in terms of energy differences.
Next, we use the notation
where h is a vector field in 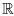 N.
N.
Lemma 4.1 (Energy identities). Let u(x, t), θ(x, t) be the solution of (1.1)-(1.4), m Є W1,∞ (Ω) and h:  →
→ 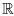 N a vector field of class C1. Then, the following identities hold.
N a vector field of class C1. Then, the following identities hold.
where η = η(x) is the outward unit normal at x Є ∂ Ω.
Proof. Equations (4.4), (4.1) and (4.2) are proved by multiplying (1.1), respectively, by the following multipliers M(u) = u, M(u) = m(x)u and M(u) = h : ∇u, followed by integration over Q(t). Equation (4.3) is a special case of equation (4.2) for h = x - xo. We used the fact that u = 0 on ∂Ω × [0, ∞) and, as a consequence, the following vector identity:
□
on ∂Ω × [0, ∞).
5 Energy estimates
In this and the next sections, the symbol C may denote different positive constants. These constants depend on, at most, |Ω|,|a|∞ and the initial data.
The idea to obtain the stabilization of the energy (to zero) is to show an estimate for the energy, as follows:
 E(s)1+δ < C (E(t) - E(t + T)) for all t > 0,
E(s)1+δ < C (E(t) - E(t + T)) for all t > 0,
for some positive δ and a fixed T > 0, which may be large.
Then the asymptotic behavior is obtained using the following Lemma:
Lemma 5.1 (Nakao [13]). Let Φ(t) be a nonnegative function on 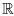 + satisfying
+ satisfying
 Φ(s)1+δ < C1 {Φ(t) - Φ(t + T)}
Φ(s)1+δ < C1 {Φ(t) - Φ(t + T)}
with T > 0, δ > 0 and C1 a positive constant. Then Φ(t) has the decay property
Φ(t)< C1Φ(0) (1+t)-1/δ, t > T
where C 1 is a positive constant.
If δ = 0, then Φ(t) has the decay property (exponential decay)
Φ(t) < C1Φ(0) exp-κ t,
for positive constants κ and C 1 .
We also include the following lemma, which will be used to estimate an integral involving the dissipative term ρ.
Lemma 5.2 (Gagliardo-Nirenberg). Let 1 < r < p < ∞, 1 < q < p and 0 < m. Then,
for v Î Wm,p (Ω) ∩ Lr(Ω), Ω ⊂ 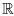 N, where C2 is a positive constant and
N, where C2 is a positive constant and
provided that 0 < q < 1.
Now, we begin the estimates for the energy of (1.1).
Lemma 5.3. Let β > 0 such that  -1 > 0 and γ = 2 min{γ1, γ2}, where γ1 = (
-1 > 0 and γ = 2 min{γ1, γ2}, where γ1 = ( - 1) and γ2 = (1 + β (1 -
- 1) and γ2 = (1 + β (1 -  )). Then,
)). Then,
for all t> 0, T > 0, where Mo =  |x - xo|.
|x - xo|.
The proof is obtained multiplying the identity (4.3) by β and adding with the identity (4.4). The details are similar to Oliveira-Charão ([14]) for an incompressible vector wave equation.
It is necessary to estimate the boundary integral which appear in the above lemma.
Lemma 5.4. There exists a constant C > 0 such that
Proof. Let h : 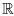 N→
N→ 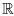 Nbe a vector field of class C1over
Nbe a vector field of class C1over  which satisfies:
which satisfies:
where η = η(x) is the outward unit normal vector at x Є ∂ Ω,  ⊂
⊂ 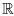 N is an open set such that Γ(xo) ⊂
N is an open set such that Γ(xo) ⊂  ∩
∩  ⊂ w ⊂
⊂ w ⊂  .
.
Let m Є W1,∞ (Ω) be a function such that
For the existence of such functions, see [4, 10].
Using identity (4.2), the properties of h, m and the summation convention, we have:
Therefore,
Since, by Poincare's inequality,
we estimate ∫Q(t) m(x) [a2 |∇u|2 + (b2 - a2) (div u)2] dxds using identity (4.1) and the properties of m:
Now, using Young's inequality in the last integral, the fact that  isbounded and absorbing the term with the divergence in the left-hand side, we obtain
isbounded and absorbing the term with the divergence in the left-hand side, we obtain
For the last estimate we have also used the inequality:
Combining the previous estimates, the proof of Lemma 5.4 follows.
□
Lemma 5.5. Let u(x, t) be the solution of (1.1)-(1.4). There exists a constant T > 0, which depends on E(0), such that
for all t > 0.
Proof. It follows from the identity in Remark 2 that
This fact allows us to get an estimate for the total energy E(t).
Because the energy decreases, we have: T E(t + T) <  E(s) ds.
E(s) ds.
These facts and the last two lemmas imply that:
Thus, if we choose a fixed T such that T > 2 C1 + 1, the lemma is proved.
Lemma 5.6. Let (u, θ) be the solution of (1.1)-(1.4). Then, for T given by the previous lemma, we have:
If r > 0, 0 < p <  and N > 3, then
and N > 3, then
If N = 2, the estimate (5.9) holds for r > 0, p > 0.
If r > 0, -1 < p < 0 and N > 3, then
If r > 0, -1 < p < 0 and N = 2, then
If -1 < r < 0, 0 < p <  and N > 3, then
and N > 3, then
If N = 2, the estimate (5.12) holds for -1 < r < 0, p > 0.
If -1 < r < 0, -1 < p < 0 and N > 3, then
If -1 < r < 0, -1 < p < 0 and N = 2, then
The numbers r and p appear in hypothesis (H2)(d) on the growth of the functionρ.
Proof. By hypotheses on the growth of ρ, we have
for t > 0, where
Ω1 = Ω1(t) = {x Є Ω, |ut(x, t)| < 1}, Ω2 = Ω\Ω1.
We will use the following estimate as a consequence of Gagliardo-Nirenberg's Lemma, Poincare's inequality and the boundedness of the L2-norm of Δu,
with θ =  .
.
Case 1: Estimating I1 for r > 0, N > 2:
Using Poincare's inequality we obtain
because
where C depends on |Ω|,  and the fixed number T. We have used the fact that E(t) is a non increasing function of t.
and the fixed number T. We have used the fact that E(t) is a non increasing function of t.
Using the hypotheses H2(a), H2(d) and identity (2.2) in Remark 2, it follows that
Case 2: Estimating I1 for -1 < r < 0, N > 2:
Using Hölder's inequality, Poincaré's inequality in  (Ω)N and hypotheses H2(a), H2(d), we obtain
(Ω)N and hypotheses H2(a), H2(d), we obtain
Case 3: Estimating I2 for 0 < p <  , N > 3 ( or p > 0 if N = 2):
, N > 3 ( or p > 0 if N = 2):
where we have used Poincaré's inequality in  (Ω)N, Hölder's inequality and the hypothesis in (H2)(d) on the boundedness of a(x).
(Ω)N, Hölder's inequality and the hypothesis in (H2)(d) on the boundedness of a(x).
Now, the hypothesis H2(d), identity (2.2) in Remark 2 and estimate (5.15) imply
Case 4a: Estimating I2 for -1 < p < 0, N > 3:
Thus,
where l' is the conjugate exponent of l.
Now, choosing
we have l' =  and
and
since ut Є L∞ ([0, ∞); 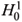 (Ω)N)
(Ω)N)  L∞ ([0, ∞);
L∞ ([0, ∞);  (Ω)N) due to Lemma 3.4 and Sobolev's inequality. The positive constant C depends also on the initial data.
(Ω)N) due to Lemma 3.4 and Sobolev's inequality. The positive constant C depends also on the initial data.
Case 4b: Estimating I2 for -1 < p < 0, N = 2:
Then, using Poincaré's inequality for u Є  (Ω) and the hypotheses on the function ρ(x, s), it follows that
(Ω) and the hypotheses on the function ρ(x, s), it follows that
Now, using the inequality of Gagliardo-Nirenberg (Lemma 5.2) with θ =  it follows that
it follows that
Then, by Remark 2 and the boundedness of Δu (proved in a previous section), we obtain
6 Main estimates for stabilization
Using Young's inequality and Lemmas 5.5, 5.6, we obtain the next result.
Proposition 6.1. The energy for the solution of problem (1.1)-(1.4) satisfies
i = 1,2,3,4, where
Now, using Poincare's and Young's inequalities, we obtain (with ∈0 =  )
)
In the last inequality we have used the identity mentioned in Remark 2.
Using the above estimate in (6.1), we obtain
Thus, the natural dissipation of the system reduced the proof of the theorem of stabilization to the following estimate.
Proposition 6.2. Let R > 0 fixed and {u, θ} be the solution of the problem (1.1)-(1.4). Let uo, u1 and θo be such that E(0) < R. Then, there exists a constant C > 0 such that
where T > 0 is given by Lemma 5.5, the constant C depends on R. Here i = 1, 2, 3, 4 according to the cases previously described.
Proof. We present the proof by contradiction for N > 3 (the proof for N = 2 is easier). Suppose there exists a sequence of solutions  with the following corresponding initial data
with the following corresponding initial data  and a sequence
and a sequence  Ω
Ω  + such that
+ such that
Let
and
Then, from (6.4), we obtain
Let vn (x, t) =  and ηn(x, t) =
and ηn(x, t) =  , 0 < t < T. Furthermore, from (6.5), we have that
, 0 < t < T. Furthermore, from (6.5), we have that
for all n Є  .
.
The estimate (6.1) together com (6.7) and (6.8) imply that
But, In(tn) is bounded due to (6.7). Therefore, we obtain that
for all 0 < t < T and for all n Є  , where C > 0 does not depend on t and n. Therefore,
, where C > 0 does not depend on t and n. Therefore,
for all 0 < t < T and for all n Є  . However, from Poincaré's inequality and from the estimate (6.9), it follows that
. However, from Poincaré's inequality and from the estimate (6.9), it follows that
for all 0 < t < T and for all n Є  .
.
Thus, there exists a constant C > 0 such that
for all 0 < t < T and for all n Є  .
.
We conclude that
for all n Є  .
.
Now, we claim that
First we prove this claim for the case where r > 0 and 0 < p <  .
.
For the case r > 0 and 0 < p <  , proceeding as we did previously when we defined regions Ω1(t), Ω2(t) to estimate I1 and I2, we obtain
, proceeding as we did previously when we defined regions Ω1(t), Ω2(t) to estimate I1 and I2, we obtain
where C depends on T, |Ω| and ||a||∞. Now, using the definition of D1(t)
By (6.6),
where
However, {λn}n> 1 is a bounded sequence:
Hence, (6.7) and the definition of In imply that
as m goes to ∞.
The remaining cases are treated similarly. We have proved that
Thefore, (6.12) is proved.
At this point, we shall prove that
To prove (6.16), we use Cauchy-Schwarz's inequality to obtain
Then,
when n → ∞.
Then, (6.16) holds.
Also, we need to show that
From (6.7) we have that
then
since vn → v weak- in L2(0, T; [L2(Ω)]N).
in L2(0, T; [L2(Ω)]N).
So, (6.19) is proved.
Finally, we prove that
From Cauchy-Schwarz's inequality, we have that
Therefore, (6.20) holds.
Now, we pass to the limit of  . From (6.11) it follows that there are function v(t), η(t) and subsequences of the sequences vn and ηn, which we continue to represent by vn and ηn such that
. From (6.11) it follows that there are function v(t), η(t) and subsequences of the sequences vn and ηn, which we continue to represent by vn and ηn such that
vn (t)  v(t) weak
v(t) weak  in W1, ∞ (0, T; [L2 (Ω)]N) ∩ L∞ (0, T;
in W1, ∞ (0, T; [L2 (Ω)]N) ∩ L∞ (0, T;  (Ω)]N)
(Ω)]N)
ηn (t)  η(t) weak
η(t) weak  in L∞(0, T; L2 (Ω)).
in L∞(0, T; L2 (Ω)).
Therefore, the functions v(t) and η(t) satisfy:
i) v Є W1, ∞ (0, T; [L2 (Ω)]N) ∩ L∞ (0, T;
(Ω)]N) and η Є L∞(0, T; L2 (Ω));
ii) vtt - a2Δv - (b2 - a2) ∇(div v) = 0,
iii) ηt - Δη + div vt = 0,
iv)
|vt|2dxds = 0,
v)
|v|2dxds = 1.
We observe that {η, vt} is also solution of equations ii), iii). Since vt = 0 a.e. in ω × (0, T) and (vt)" -a2Δ(vt) - (b2 - a2) ∇(div vt) = 0 with homogeneous Dirichlet boundary conditions, it follows from a consequence of Holmgren's Uniqueness Theorem ([11], p. 88) that vt = 0 in Ω × (0, T), therefore v(x, t) = F(x) a.e. in Ω × (0, T). Thus, v satisfies -a2Δv -(b2 - a2) ∇¸ v = 0 with homogeneous Dirichlet boundary conditions. From the uniqueness of this Dirichlet problem, it results that v = 0 a.e. in (0, T) × Ω. This contradicts the item (v).
□
The following estimate is a consequence of the previous proposition.
Proposition 6.3.
where Di(t) (i = 1,2,3,4) are given in Proposition 6.1.
7 Proof of the theorem of stabilization
Now, it remains to estimate the integral ∫Qω(t)|ut|2dx ds in terms of ΔE (energy difference).
Proof. Case a:r> 0 and 0 < p <  if N > 3 (r > 0, p > 0 if N = 2):
if N > 3 (r > 0, p > 0 if N = 2):
Using the hypothesis on ω in (H2)(d), Hölder's inequality and the definitions of Ω1, Ω2, we obtain
where the last C depends on |Ω|, T and ||a||∞.
Then, due to Remark 2, we have
From estimates (6.21) and (7.1), and the expression for D1(t) we obtain
Then, using the fact that E(t) is nonincreasing function of t, we obtain that
where
is such that 0 < K1< 1 and C is a positive constant which depends on the initial data.
We have obtained the following inequality
If we set 1 + γ =  , then γ =
, then γ =  and applying Nakao's Lemma to (7.3) we obtain for N > 3 that
and applying Nakao's Lemma to (7.3) we obtain for N > 3 that
with We see from (7.2) that if r = p = 0, then according to Nakao's Lemma, the decay rate is exponential. If r = 0, p > 0, then the decay rate depends only on p : γ1 =  ; and if r > 0, p = 0, then the decay rate depends only on r : γ1 =
; and if r > 0, p = 0, then the decay rate depends only on r : γ1 =  .
.
If N = 2, r > 0 and p > 0 then γ1 =  . If N = 2, r = 0 and p > 0 then the decay rate is exponential.
. If N = 2, r = 0 and p > 0 then the decay rate is exponential.
Case b: r> 0 and -1 < p < 0 and N > 2:
In this case we have
Then, in the same way as in case (a), we get
Now, assuming that N > 3 and considering (6.21), (7.5) and the definition of D2(t) we have
If we define
then we have 0 < K2 < 1 and
 .
.
Similarly to the case (a), using Nakao's Lemma, we obtain
with
From (7.6), it follows that if r = 0 then γ2 =  .
.
When N = 2, (6.21), (7.5) and the definition of D2(t) imply that
If r = 0, then E(t) < C ΔE. Thus, by Nakao's Lemma, we obtain exponential decay of the energy.
If r > 0, we obtain
with
Applying Nakao's Lemma, we obtain
with γ2 =  .
.
Case c: -1 < r < 0 and 0 < p <  (-1 < r < 0, p > 0 if N = 2):
(-1 < r < 0, p > 0 if N = 2):
We have
and it follows that
Thus, from (6.21), (7.8) and the definition of D3(t), we get
Therefore
with
is such that 0 < K3 < 1.
We conclude by Nakao's Lemma,
with
From (7.10) it follows that γ3 =  if p = 0 and N > 3 or N = 2 and p > 0.
if p = 0 and N > 3 or N = 2 and p > 0.
Case d: -1 < r < 0, -1 < p < 0 and N > 2:
We have
Assuming that N > 3, it follows from (6.21), the definition of D4(t) and the previous inequality that
Thus, we get
with
Then, using Nakao's Lemma, we obtain
with
Now we consider N = 2. It follows from (6.21), the definition of D4(t) and the inequality at the beginning of this case that
Thus,
with K4 =  .
.
Then, using Nakao's Lemma, we obtain
with γ4 =  .
.
Now, the proof of the Theorem 3.7 is complete.
□
Acknowledgments. The authors would like to thank the referees for thevaluable comments and important suggestions which have substantially improved this paper.
Received: 21/IX/07. Accepted: 22VII/08.
#735/07.
- [1] E. Bisognin, V. Bisognin and R.C. Charão, Uniform stabilization for elastic waves system with highly nonlinear localized dissipation Portugaliae Mathematica, 60 (2003), 99-124.
- [2] C.M. Dafermos, On the existence and asymptotic stability of solution to the equation of linear thermoelasticity Arch. Rat. Mech. Anal., 29 (1968), 241-247.
- [3] A. Guesmia, On the decay estimates for elasticity systems with some localized dissipations Asymptotic Analysis, 22 (2000), 1-13.
- [4] A. Haraux, Semigroupes linéaires et équations d'évolution linéaires périodiques Université Pierre et Marie Curie, Paris, (1978) number 78011.
- [5] D. Henry, O. Lopes and A. Perisinotto, Linear thermoelasticity asymptotic stability and essential spectrum Nonlinear Analysis, Theory and Applications, 21(1) (1993), 65-75.
- [6] T. Irmscher and R. Racke, Sharp decay rates in parabolic and hyperbolic thermoelasticity IMA Journal of Applied Mathematics, 71 (2006), 459-478.
- [7] S. Jiang, J.E. Muñoz Rivera and R. Racke, Asymptotic stability and global existence in thermoelasticity with symmetry Quart. Appl. Math., 56(2) (1998), 259-275.
- [8] V. Komornik, Exact controllability and stabilization, the multiplier method John Wiley & Sons - Masson, (1994), Paris.
- [9] G. Lebeau and E. Zuazua, Decay rates for the three-dimensional linear system of thermoelasticity Arch. Rat. Mach. Anal., 148 (1999), 179-231.
- [10] J.L. Lions, Exact controllability, stabilization and perturbations for distributed systems SIAM Rev., 30 (1988), 1-68.
- [11] J.L. Lions, Contrôlabilité Exacte Perturbations et Stabilization de Systèmes Distribués. Tome 1: Contrôlabilité Exacte RMA 8, Masson, Paris, 1988.
- [12] W.J. Liu and E. Zuazua, Uniform stabilization of the higher-dimentional system of thermoelasticity with nonlinear boundary feedback Quart. Appl. Math., 59(2) (2001), 269-314.
- [13] M. Nakao, Decay of solutions of the wave equation with a local nonlinear dissipation Math. Ann., 305 (1996), 403-417.
- [14] J.C. Oliveira and R.C. Charão, Stabilization of a locally damped incompressible wave equation J. Math. Anal. Appl., 303 (2005), 699-725.
- [15] D.C. Pereira and G.P. Menzala, Exponential decay of solutions to a coupled system of equations of linear thermoelasticity Mat. Aplic., 8(3) (1989), 193-204.
- [16] Y. Qin and J.E.M. Rivera, Global existence and exponential stability of solutions to thermoelastic equations of hyperbolic type J. Elasticity, 75(2) (2004), 125-145.
- [17] R. Racke, On the Cauchy problem in nonlinear 3-d thermoelasticity Math. Z., 203(4) (1990), 649-682.
- [18] R. Racke, Exponential decay for a class of initial-boundary value problems in thermoelasticity Mat. Apl. Comput., 12(1) (1993), 67-80.
- [19] R. Racke and Y. Shibata, Global smooth solutions and asymptotic stability in one-dimensional nonlinear thermoelasticity Arch. Rational Mech. Anal., 116(1) (1991), 1-34.
- [20] R. Racke, Y. Shibata and S.M. Zheng, Global solvability and exponential stability on one-dimensional nonlinear thermoelasticity Quart. Appl. Math., 51(4) (1993), 751-763.
- [21] J.E.M. Rivera, Asymptotic behaviour in n-dimensional thermoelasticity Appl. Math. Lett., 10(5) (1997), 47-53.
- [22] J.E.M. Rivera, Asymptotic behaviour in inhomogeneous linear thermoelasticity Appl. Anal., 53(1-2) (1994), 55-65.
- [23] J.E.M. Rivera, Energy decay rates in linear thermoelasticity Funkcialaj Ekvacioj, 35(1) (1992), 19-30.
- [24] J.E.M. Rivera and R.K. Barreto, Existence and exponential decay in nonlinear thermoelasticity Nonlinear Anal., 31(1) (1998), 149-162.
Publication Dates
-
Publication in this collection
29 Oct 2008 -
Date of issue
2008
History
-
Received
21 Sept 2007 -
Accepted
22 July 2008










































































































































