A 1D-FDM Transmission Line Model for Partial Discharge Current Simulations Validated Against Needle-Plate HVDC Laboratory Experiments: Calculations of Ionized Air Conductivity

Abstract

In this paper, we present a novel numerical model for simulating partial discharges (PDs) transient currents excited by high-voltage DC (HVDC) systems. The model is based on the telegraph equations, which are solved in the time domain via the finite-difference method (FDM). With the proposed model, one can simulate air ionization through its distinct phases based on the electric field’s magnitude. This study specifically provides effective electrical conductivity of ionized air over time and space, calculated in the discharge channel also as a function of voltage and gap distance in a needle-plate setup. Validation is performed against experimental results from our laboratory experiments, demonstrating agreement despite the model’s one-dimensional nature. The simplicity of the model leads to much smaller simulation times (up to two minutes) compared to more complex three-dimensional models (typically requiring hours to complete), highlighting its potential for efficient PD analysis and future developments of general PD models based on effective plasma conductivity.

Index Terms
Effective Electrical Conductivity; Finite-Difference Method; High-Voltage Direct Current (HVDC); Partial Discharges.

I. INTRODUCTION

The reliable operation of high-voltage equipment such as synchronous generators heavily relies on the integrity of their insulation systems. However, continuous operation inevitably leads to insulation degradation. Irregularities within the insulation, whether inherent during manufacturing or acquired through usage (e.g., delamination, thermal stress, erosion, electrical stress), can give rise to partial discharges (PDs) [¹]. PDs are localized electrical breakdowns that occur within the insulation of highvoltage equipment when subjected to high electric fields.

The adoption of high-voltage direct current (HVDC) technology has witnessed a surge in recent years, leading to increased focus on the significance of DC partial discharges (DC-PDs) [²]. While HVDC applications have historically received less attention than their alternating current (AC) counterparts [²], the importance of DC-PDs is becoming increasingly evident. These discharges can act as indicators of insulation defects, contributing to insulation aging and degradation [³].

Although PD monitoring in AC systems has been extensively studied and widely implemented for predictive maintenance [⁴], research on PDs under DC conditions remains relatively sparse [³]. A key difference in PD phenomena under DC lies in the unidirectional flow of current, resulting in PDs typically exhibiting the same polarity [⁵]. Furthermore, the accumulation of charges within insulation materials or at interfaces can temporarily suppress PD activity, leading to less frequent PD occurrences compared to AC conditions [³]. Despite their less frequent nature, DC-PDs remain indicative of potential insulation weaknesses, highlighting the crucial need for effective techniques to interpret DC-PD activity [³], [⁵].

While controlled laboratory environments might appear distinct from the intricate nature of real-world HVDC systems, they provide a valuable foundation for understanding and mitigating partial discharge (PD) phenomena. A classic example is the needle-plate configuration, often studied to gain insights into PD behavior [⁶]. This setup, based standard needles with micrometric tips, offers a well-defined geometry with controllable parameters, enabling researchers to isolate and investigate the fundamental mechanisms governing PD initiation and evolution [⁶], [⁷].

Numerical methods have been proposed to represent PD phenomena [⁸]-[¹⁰]. For instance, Hoshino et al. [⁹] utilized a precise finite-difference time-domain (FDTD) model of a gas-insulated switchgear (GIS) to analyze the transient electromagnetic pulses from PDs, enabling the evaluation and calibration of ultra-high frequency (UHF) couplers. Oliveira et al. [¹⁰] developed a novel model for locating PDs in hydrogenerators’ stator bars. Their numerical model, based on the FDTD method, determined the resonance frequencies of propagation channels between the PD source and a voltage sensor within the hydrogenerator coil, producing a probability map of PD occurrence which was used for PD pinpointing. Streamer discharge models generally combine electrostatic principles with the dynamics of charged particles, including electrons and positive and negative ions. This combination forms a system of equations where convection-diffusion-reaction equations for particle transport are coupled with the stationary Poisson equation for the electric field. Even with advanced supercomputing resources, the computational demands for simulating streamer propagation are substantial due to the nonlinear behavior of ionized materials, the presence of source terms, and the complex interactions between electron density and the electric field. In [⁶], an extended Sato equation [¹¹] was applied to simulate air ionization, but electromagnetic wave behavior was not explored. The original Sato equation [¹²] was designed to compute currents under a constant applied voltage based on energy balance. Its extended form, however, allows for current calculations with time-dependent voltages. In [¹³], discharge current equations were derived from Ampere’s law, Gauss’s divergence theorem, and the Poynting vector, allowing simulations of currents and sound waves produced by partial discharges under high continuous voltages through coupling with the Navier-Stokes equations. Two-dimensional modeling of a needle-plate configuration using finite elements was performed in [¹⁴], where the electric field was determined by solving the Poisson equation. Similarly, air ionization in corona discharges was modeled using the recursive least squares (RLS) approach in [¹⁵], where the plasma channel was represented by a resistor and capacitor in series, capturing the ionization in the air gap. In [¹⁶], a magnetohydrodynamic model was employed for plasma filament modelling, accounting for constant electrical conductivities as well as the arc’s growth both parallelly and perpendicularly to a composite weave. The transient current profile in partially ionized air was influenced by the time-dependent diameter of the plasma filament, temperature, and pressure. Lastly, Loubani et al. [¹⁷] utilized the finite-difference time-domain (FDTD) method to model electromagnetic fields emitted by a partial discharge source. This source was represented by a basic current source filament.

Despite all the complexities of the physical phenomena, the described multi-physics problem, involving thermodynamics, fluid dynamics and electromagnetics, ultimately results in an effective electric conductivity σ of the ionized material. Therefore, the goal of this work is the calculation of effective electric conductivity of ionized air, over time and space, which is a function of gap distance and applied voltage for the needle-plate problem [⁶]. Effective electrical conductivity was numerically obtained over time and space as a function of gap distance and voltage, based on experimental data produced in this work. Our numerical model is based on an one-dimensional transmission line formulation based on the telegraph equations [¹⁸]. The simulations were performed using a custom-developed C program, employing a central finite-difference scheme [¹⁹] to solve the telegraph equations in the time domain. Specifically, the ionized air conductivity is calculated to replicate our experimental conditions of a steel needle with tip diameter measuring 40 µm, and by varying the gap distance (the range 4 mm - 8 mm was considered). The experiments were carefully designed to ensure consistent relative humidity levels and temperature, minimizing variability in the measured waveforms. Finally, our fast processing transmission line model can help to perform fast parametric studies and support development of plasma conductivity models.

II. A BRIEF REVIEW ON PHYSICS OF PARTIAL DISCHARGES

Partial discharges in air are significantly influenced by the reduced electric field E/n, where E represents the electric field strength and n denotes the local gas density [²⁰]. When the reduced electric field surpasses a critical value (E/n)_crit, the ionization coefficient of air becomes larger than the attachment coefficient, leading to a rapid increase in the number of free electrons and the initiation of a discharge [²⁰].

In the context of the needle-plane electrode configuration used in this study, the electric field is highly non-uniform, with a pronounced concentration near the tip of the anode needle electrode. This field intensification facilitates the initiation of a discharge at voltages lower than those required for a uniform field breakdown. Fig. 1 illustrates the different stages of streamer formation and propagation. The graph on the left of each sub-figure (blue line) depicts the reduced electric field along the gap longitudinal axis, while the images on the right provide a visual representation of the discharge development. Streamer formation in a non-uniform electric field involves several sequential phases, illustrated schematically in Figs. 1(a) to 1(h). Initially, a high voltage is applied, creating a strong electric field near the anode (Fig. 1(a)). This field accelerates free electrons, causing collisions with neutral gas molecules and generating ion pairs (Fig. 1(b)). Electrons, being lighter, drift rapidly towards the anode, enhancing the local field at the channel tip and leading to further ionization (Fig. 1(c)). This creates a thin ionization region, or streamer head, that propagates towards the cathode (Fig. 1(d)). As the ionization front advances, it leaves behind a quasi-neutral plasma channel of cations and electrons, with a reduced internal field (Figs. 1(e)-1(g)). However, the propagating streamer accumulates space charge, specially as the channel head reaches the cathode, subjecting the channel to high voltage, thus sustaining increasing and propagating electric field necessary for continuous fast ionization for a while (Figs. 1(e)-1(h)). Subsequently, as more and more electrons are released from gas molecules, electric field diminishes, and eventually it is is under the ionization threshold (critical electric field). Remaining ions and electrons eventually recombine, electrically neutralizing the channel [²⁰].

Fig. 1
Streamer formation and its propagation in a non-uniform electric field (needle-plate setup). The blue line shows E/n along the gap axis. High voltage near the anode needle accelerates electrons, generating ion pairs (a-b). Electrons drift, enhancing streamer tip fields and ionization (c). Streamer head moving towards the cathode plate (c)-(d). Channel is subjected to high voltage (d)-(h), thus promoting fast increasing of E/n and of electric conductivity of ionized air.

Therefore, the discharge process in a needle-plane gap under a positive applied voltage can be broadly categorized into several stages:

1. Pre-Ionization: Initially, a small number of free electrons are present in the air gap mainly due to background radiation [²¹]. As the voltage is applied, these electrons accelerate due the electric field and gain sufficient energy to ionize neutral gas molecules, generating additional electron-ion pairs.

2. Streamer Formation: As the ionization process intensifies, an electron avalanche develops, leading to a rapid increase in the local electron density. This concentrated region of charged particles, known as a streamer, propagates towards the grounded plane. The streamer’s propagation is driven by the high electric field at streamer tip, which further enhances ionization [⁶], [²⁰], [²²].

3. Breakdown Streamer (BS): When the streamer reaches the grounded plane, a conductive channel is established between the high voltage electrodes and electric field increases during a small amount of time, leading to a sudden increase in electric conductivity and discharge current. This stage is characterized by a subsequent rapid drop in the voltage across the gap and the formation of a conducting plasma channel [⁶], [²⁰], [²²].

4. Deionization: Following the breakdown, the electric field in the gap redistributes, and the energy input into the plasma channel decreases. As a result, the plasma cools down, and the electrons and ions recombine, leading to a progressive decrease in conductivity. This deionization process eventually extinguishes the discharge [⁶], [²⁰], [²²].

III. THE EXPERIMENTAL SETUP AND RESULTS

Aiming at validation of the proposed numerical model, our experimental setup comprises a needleplane electrode arrangement housed within a controlled environment to regulate air humidity. Constant high voltage is applied to a steel needle, designated as the high-voltage electrode, while a copper plane serves as the grounded electrode.

The employed standard steel needle is an Ogura X-253-7 model, identical to that one utilized by Eichwald et al. in [⁶]. The needle model features a cylindrical body with a diameter of 1 mm and a conically shaped tip culminating in a spherical end with a radius of curvature of 20 µm. The ground plane consists of a 5.0 cm diameter copper-plated disc fabricated from an FR4 PCB blank. Figs. 2 and 3 respectively provide a photographic view of the needle and a magnified image of the needle tip obtained using a scanning electron microscope (SEM).

Fig. 2
Photograph of our Ogura X-253-7 standard needle and measurement of its length.

Fig. 3
SEM image of our Ogura standard needle tip and its diameter evaluation.

The experiments are conducted within an enclosed container, as depicted in Fig. 4, to maintain a relative humidity level of approximately 2% and temperature of 20^◦C under sea-level atmospheric pressure throughout the measurements. A schematic representation of the experimental setup circuit is presented in Fig. 5.

Fig. 4
Experimental setup enclosed within a controlled environment (humidity level of 2% and temperature of 20^◦C).

Fig. 5
Schematic representation of the experimental setup circuit excited by HVDC system.

The current flowing through the discharge channel is measured indirectly by monitoring the voltage drop across a 50 Ω resistor connected in series with the ground plane. A high-voltage resistor of 25 MΩ, controllably acting as a dielectric barrier, is also incorporated into the circuit to limit the discharge current and prevent the power supply’s over-current protection mechanism from triggering. We have calculated the normalized power spectrum P(f) of the experimental PD current obtained with the 8 mm gap and the applied voltage of 9347V, as Fig. 6 shows. The maximum significant frequency with appreciable power is approximately 6MHz. Additionally, we have measured the capacitance and inductance of the 50Ω resistor using the instrument Agilent E4980A LCR meter. The obtained values are L = 177.74nH and C = 56.48pF. Thus, at 6MHz, we have the stray reactances Z_L = ωL = 6.70Ω and Z_C = (ωC)^-1 = 469.65Ω. As widely known [²³], stray impedances -jZ_C and jZ_L for resistors in equivalent resistor circuits are considered to be in parallel and in series arrangements, respectively, with the resistor and with the impedance R ∥ (-jZ_C) (see the Fig. 7). Therefore, as one can see, the calculated stray reactances Z_L and Z_C are not of major concern for our case.

Fig. 6
Normalized power spectrum P(f) of experimental PD current (8 mm gap and 9.347 kV).

Fig. 7
Equivalent high-frequency resistor representation with lumped circuit elements [²³].

Current waveforms are acquired for various gap distances, specifically 4, 5, 6, 7 and 8 mm, as shown respectively by Fig. 8(a), Fig. 8(b), Fig. 8(c), Fig. 8(d) and Fig. 8(e). Table I summarizes the applied DC voltages for each gap distance and The obtained waveforms exhibit the characteristic sharp rise time associated with streamer formation and propagation, followed by a slower decay as the discharge extinguishes. These experimental results serve as reference data for evaluating the numerical model’s ability to accurately capture the dynamic behavior PD currents.

TABLE I
APPLIED DC VOLTAGES FOR DIFFERENT ELECTRODE GAP DISTANCES IN OUR LABORATORY EXPERIMENTS.

Gap (mm)	V1 (V)	V2 (V)	V3 (V)	V4 (V)	V5 (V)
8	9347	8900	8455	7818	-
7	8600	8200	7820	7180	-
6	8323	7778	7408	7048	6486
5	7314	6816	6510	6178	6025
4	6198	5801	5525	5248	4851

Fig. 8
Experimentally obtained current pulses for gap distances of: (a) 4 mm, (b) 5 mm, (c) 6 mm, (d) 7 mm, and (e) 8 mm at a relative humidity of approximately 2%.

IV. NUMERICAL FORMULATION OF TRANSMISSION LINES USING FINITE DIFFERENCES

The numerical model developed in this study is based on the telegraph equations [¹⁸] to represent the electrical behavior of the discharge channel. The telegraph equations, which are derived from Maxwell’s differential equations, describe voltage and current distributions along a transmission line over time. In their general form, the telegraph equations are given by

(1) $$\frac{\partial V(x,t)}{\partial x}=-L\frac{\partial I(x,t)}{\partial t}-RI(x,t)$$

and

(2) $$\frac{\partial I(x,t)}{\partial x}=-C\frac{\partial V(x,t)}{\partial t}-GV(x,t),$$

where V (x,t) and I(x,t) represent the voltage and current at position x and time t, respectively. The parameters R, L, C, and G denote the local per-unit length resistance, inductance, capacitance, and conductance in the transmission line, respectively.

To solve (1) and (2) numerically, the transmission line is discretized into consecutive cells of length ∆_x, as illustrated in Fig. 9 (physical cell of a transmission line) and Fig. 10 (the developed finitedifference computational cell structure). Thus, voltage and current are then computed at discrete domain points in space (separated by ∆_x) and time using a time step of ∆_t.

Fig. 9
Representation of a physical cell of a transmission line.

Fig. 10
The developed computational cell structure in our finite-difference scheme.

Fig. 11
Schematic representation of the proposed 1D discharge channel model. Finite-difference cell indexed by i_m is the last cell to which updating equations are applied.

The temporal derivatives in (1) and (2) are approximated using the central difference scheme [¹⁹]

(3) $$\frac{\partial I(x,t)}{\partial t}\approx \frac{I^{n+0.5}[i+0.5]-I^{n-0.5}[i+0.5]}{{\mathrm{\Delta }}_t}$$

and

(4) $$\frac{\partial V(x,t)}{\partial t}\approx \frac{V^{n+1}[i]-V^n[i]}{{\mathrm{\Delta }}_t},$$

where the superscript n represents the time index and the subscript i denotes the spatial index, in such a way that t = n · ∆_t and x = i · ∆_x. Space derivatives are approximated in similar way (with finite-differences) as time derivatives. Substituting finite-difference approximations into (1) and (2) and rearranging the terms, we obtain the finite-difference equations for updating current and voltage over space and time, which are given by

(5) $$I^{n+0.5}[i+0.5]=(\frac{I^{n-0.5}[i+0.5]}{{\mathrm{\Delta }}_t}-\frac{R}{L}\frac{I^{n-0.5}[i+0.5]}{2}+-\frac{1}{L}\frac{V^n[i+1]-V^n[i]}{{\mathrm{\Delta }}_x})\cdot {(\frac{1}{{\mathrm{\Delta }}_t}+\frac{R}{2L})}^{-1}$$

and

(6) $$V^{n+1}[i]=(-\frac{1}{C}\frac{I^{n+0.5}[i+0.5]-I^{n+0.5}(i-0.5)}{{\mathrm{\Delta }}_x}\frac{V^n[i]}{{\mathrm{\Delta }}_t}-\frac{G}{C}\frac{V^n[i]}{2})\cdot {(\frac{1}{{\mathrm{\Delta }}_t}+\frac{G}{2C})}^{-1}$$

Equations (5) and (6) form the basis of the numerical algorithm developed to calculate the voltage and current distribution along the discharge channel as a function of time and space.

V. CALCULATION OF ELECTRICAL CONDUCTIVITY OF DISCHARGE CHANNELS

A critical aspect of simulating PDs is accurately modeling the air ionization process, which directly affects the electrical conductivity of discharge channels. The discharge ionized channel conductivity update algorithm developed in this work is based on the approaches described in [²⁴] [²⁵]. It comprises four distinct phases: pre-ionization, Formation of Breakdown Streamer (FBS), Breakdown Streamer (BS), and deionization.

A. Pre-Ionization

Before the ionization of air, its conductivity is σ₀ ≈ 10^-9 S/m, which typically is the conductivity of non-ionized air (it can vary with environmental conditions) [²¹]. As the electric field increases, the points where the absolute magnitude of electric field exceeds a critical value E_c1 experience increase of electrical conductivity during the initial ionization phase of air molecules. The conductivity during the pre-ionization phase is modeled as a time-dependent exponential function given by

(7) $$\sigma (i,t)={\sigma }_0\cdot e^{(t-T_1[i])/{\tau }_1},$$

where σ(i,t) is the conductivity of cell i at time t, T₁[i] is the time instant when the electric field in cell i surpasses E_c1, and τ₁ is the time constant governing the conductivity rise during the first phase of FBS.

B. Formation of Breakdown Streamer (FBS)

As the conductivity increases and reaches a threshold value σ₁^T, ionization transitions to the second phase of FBS. In this second phase, the conductivity continues to increase exponentially, but with a different time constant τ₂, and the conductivity is governed by

(8) $$\sigma (i,t)={\sigma }_2[i]\cdot e^{(t-T_2[i])/{\tau }_2},$$

where σ₂[i] is the conductivity at cell i at time T₂[i], the instant when σ(i,t) surpasses σ₁^T.

C. Breakdown Streamer (BS)

The FBS phase continues until the conductivity across the entire discharge channel reaches a second threshold σ₂^T. At this moment, the breakdown streamer phase begins, characterized by a rapid increase of current due to the formation of a highly conductive plasma channel. During the BS phase, the ionized channel conductivity is governed by

(9) $$\sigma (i,t)={\sigma }_3[i]\cdot e^{(t-T_3)/{\tau }_3},$$

where σ₃[i] is the conductivity at cell i at time T₃, the instant when the entire channel conductivity exceeds σ₂^T, and τ₃ is the time constant for the BS phase.

During the BS phase, the critical electric field for streamer propagation is dynamically adjusted based on the conductivity of the neighboring cells. When the conductivity of cell i reaches or exceeds 40% of the conductivity of cell i - 1, the critical electric field E_c[i] at cell i is updated according to

(10) $$E_c[i]=E_{c1}+(E_{c2}-E_{c1})\cdot \left(\frac{t-T_3}{m}\right),$$

where E_c2 is the final critical electric field and 1/m represents the temporal growth rate of the critical field [²²].

D. Deionization

As the discharge progresses, the electric field in the gap redistributes, and the energy supplied to the plasma channel diminishes. Consequently, the plasma cools down and the electrons and ions start to recombine, leading to a decrease in the channel’s conductivity. This marks the beginning of the deionization phase.

The deionization process is modeled as an exponential decay of conductivity towards its initial value, i.e., the non-ionized air conductivity σ₀. The deionization time constant τ_d(i,t) varies dynamically to account for the varying recombination rates at different plasma temperatures. The conductivity update equation during deionization is given by

(11) $$\frac{1}{\sigma (i,t)}=\frac{1}{{\sigma }_d[i]}+(\frac{1}{{\sigma }_0}-\frac{1}{{\sigma }_d[i]})\cdot (1-e^{\frac{t-T_d[i]}{{\tau }_d(t,t)}}),$$

where σ_d[i] is the conductivity at cell i at the beginning of the deionization phase at time T_d[i]. The time-dependent deionization time constant τ_d(i,t) is calculated by

(12) $${\tau }_d(i,t)={\tau }_{d2}+({\tau }_{d1}-{\tau }_{d2})\cdot (1-\frac{1}{e^{c_1(t-T_d[i]-c_2)}}),$$

where τ_d1 and τ_d2 are the limits of the time constant τ_d, and c₁ and c₂ control the temporal evolution rate of τ_d [¹⁰].

VI. NUMERICAL MODELING

The numerical model developed in this work aims to represent a one-dimensional (1D) discharge channel, as illustrated in Fig. 11. The channel is divided into computational cells with a spatial step ∆_x = 0.2 mm. Two additional cells at the boundaries of the computational domain represent the anode and cathode electrodes.

The time step ∆_t is chosen to ensure numerical stability based on the Courant-Friedrichs-Lewy (CFL) condition [²⁶]

(13) $${\mathrm{\Delta }}_t\le \frac{{\mathrm{\Delta }}_x}{V_{max}},$$

where V_max represents the maximum wave propagation speed within the simulation domain. For the transmission line model, the maximum propagation speed is determined by

(14) $$V_{max}=\frac{1}{\sqrt{LC}}.$$

Using the parameters listed in Table II, a time step of ∆_t ≈ 660.46 fs is used for the simulations. The model parameters, including the distributed resistance, inductance, capacitance and conductance of the discharge channel are carefully selected to represent the physical properties of the experimental setup. The parameters for the anode cell are determined based on the experimental work of [⁶] to ensure consistency. The self-inductance of the rods used in the experiment is calculated using the formula for a cylindrical rod [²⁷] given by

TABLE II
CALCULATED AND OPTIMIZED PARAMETERS USED TO NUMERICALLY SOLVE THE TELEGRAPH EQUATIONS.

Parameter	Description	Numeric Value
∆x	Length of computational cell	0.20 mm
∆t	Time step	660.456908 fs
Rcirc	Distributed resistance (circuit equivalent)	5.0 MΩ/m
Lcirc	Distributed inductance (circuit equivalent)	215.86 µH/m
R 0	Initial distributed resistance of the gap	31.83099 GΩ/m
L	Distributed inductance of the gap	3.236329 µH/m
G	Distributed conductance	0.3 nS/m
C	Distributed capacitance	3.4380 pF/m

(15) $$L_{\mathrm{eq}}=\frac{2}{1000}l\cdot ({\log }_e\left(\frac{4l}{D}\right)-\frac{3}{4}),$$

in which L_eq is given in µH, and where l denotes the total length of the rods (cm), D is the diameter of the rods (cm). The distributed inductance L_circ used in the anode cell is obtained by considering l = 4.25 cm and D = 0.05 cm and by dividing the equivalent inductance L_eq by the cell length ∆_x = 0.20 mm. Therefore, we have L_eq ≈ 0.043171 µH and L_circ ≈ 215.86 µH/m.

The distributed gap resistance R is a time-varying parameter determined by the conductivity equations given in the previous section. The remaining model parameters, including R_circ, L, G, and C, are determined through optimization to obtain the best agreement between the simulation results and the experimental data. These parameters are listed in Table II.

VII. ALGORITHM DESCRIPTION, RESULTS AND DISCUSSION

In the proposed algorithm, we employ the developed finite-difference telegraph equations (5) and (6) for calculating current and voltage over space and time and we update the conductivity of the discharge channel using (7)-(12). The parameters given by (13)-(15) and Table II are used in all simulations.

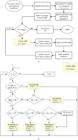
Two state variables, S and V_e, are used to control and track the simulation stages. These state variables, along with their functionalities, are listed in Table III. The state ’0’ represents ’no,’ while ’1’ represents ’yes.’ To monitor the ionization phase of each cell, a flag variable flag[i] is assigned to each cell i. The flag values associated to the various phases are summarized in Table IV. Fig. 12 presents a flowchart of the implemented algorithm (the programming language C has been used). Fig. 12(a) presents a general overview of the algorithm, which is similar to the classical FDTD method [¹⁹]: instead of electric and magnetic fields, voltages and currents are calculated and σ(t) is updated over space each time step during ionization and deionization phases. Fig. 12(b) shows the algorithmic details on calculation of σ(t), which implements the different ionization phases, just as previously described in Section V.

TABLE III
STATE VARIABLES.

Variable	Description
S	Indicates whether σ[i] ≥ σ2 for all cells
Ve	Indicates whether the ionization phase has started

TABLE IV
VALUES ASSUMED BY FLAG[I] AS DEFINED FOR THE VARIOUS IONIZATION PHASES AT EACH CELL INDEXED BY I.

Flag Value	Ionization Phase
0	Non-ionized
1	FBS 1
2	FBS 2
3	BS
4	Deionization

Fig. 12
The proposed method: (a) the general algorithm and (b) calculation of conductivity over space (k_c = 0.40).

The developed numerical model is used to simulate PDs for various gap distances and applied voltages, matching the experimental conditions described in Section III. The electric field and resistance in each cell are calculated respectively using

(16) $$E^n[i]=\frac{V^n[i]}{{\mathrm{\Delta }}_x}$$

and

(17) $$R^n[i]=\frac{{\mathrm{\Delta }}_x}{(1.087\times {10}^5{\sigma }^n[i])\cdot \pi {\left({\mathrm{\Delta }}_x/2\right)}^2\cdot {\mathrm{\Delta }}_x},$$

where Eⁿ[i] is the electric field in cell i at time t, V ⁿ[i] is the voltage at cell i, Rⁿ[i] is the per-unit length resistance at cell i at time t. Equation (17) is based on the classic resistance formula, where the effective channel conductivity is 1.087×10⁵σⁿ[i]. We may say that σⁿ[i] is a scaled conductivity, since the parameter 1.087×10⁵ is included to take into account the effects of the plasma channel diameter. In our numerical model, the applied high-voltage is that defined in [⁶], a sigmoid-like function, therefore assuming a constant value during its steady-state period corresponding to the experimental voltage applied across the electrodes in this work for each case, as listed in Table I. The ionization parameters for each gap distance and applied voltage are determined via simplex parametric optimization [²⁸] and they are presented in Tables V-IX. In order to obtain the ionization parameters, the simplex optimization guiding criteria is the absolute difference between the experimental current curves and the numerically obtained results computed over time for each gap length and the corresponding applied voltage. Thus, for each case, a combination of tuned ionization parameters minimizing the maximum absolute current difference over time has been selected. L and C were also included in the optimization process, but they were tied together by (14) for properly characterizing propagation speed of voltage (which depends on electric field traveling at the speed of light). L and C obtained for every case converged to the values given in Table II. The initial distributed gap resistance R₀ is dependent on the initial air conductivity, which is approximately 1.0 nS/m [²¹].

TABLE V
OPTIMIZED IONIZATION PARAMETERS OBTAINED FOR THE GAP DISTANCE OF 4 MM.

V[0] (V)	τ1 (ns)	τ2 (ns)	τ3 (ns)	τd1 (µs)	τd2 (ns)	c1 (Ms)	c2 (ns)	σ1 (nS)	σ2 (µS)	Ec1 (kV/m)	Ec2 (MV/m)	m (ns)
4851	6.3	29.0	2.30	5.50	60.0	10.0	10.0	440.0	1.17	967.0	24.50	4.56
5248	4.5	20.0	2.10	8.00	60.0	10.0	10.0	510.0	1.50	967.0	26.50	4.56
5525	2.7	12.5	1.85	9.00	60.0	10.0	10.0	560.0	2.00	967.0	27.90	4.56
5801	2.3	11.0	1.73	11.0	60.0	10.0	10.0	645.0	2.20	967.0	29.30	4.56
6198	2.2	8.50	1.53	13.50	60.0	10.0	10.0	755.0	2.35	967.0	31.30	4.56

TABLE VI
OPTIMIZED IONIZATION PARAMETERS OBTAINED FOR THE GAP DISTANCE OF 5 MM.

V[0] (V)	τ1 (ns)	τ2 (ns)	τ3 (ns)	τd1 (µs)	τd2 (ns)	c1 (Ms)	c2 (ns)	σ1 (nS)	σ2 (µS)	Ec1 (kV/m)	Ec2 (MV/m)	m (ns)
6025	5.7	26.0	3.10	10.0	60.0	10.0	10.0	700.0	1.90	967.0	30.40	4.56
6178	4.0	20.0	2.30	12.5	60.0	10.0	10.0	770.0	2.10	967.0	31.20	4.56
6510	2.3	18.0	2.25	14.5	60.0	10.0	10.0	780.0	2.32	967.0	32.90	4.56
6816	1.8	15.5	2.17	15.0	60.0	10.0	10.0	790.0	2.55	967.0	34.40	4.56
7314	1.7	11.3	1.95	17.0	60.0	10.0	10.0	850.0	3.10	967.0	36.90	4.56

TABLE VII
OPTIMIZED IONIZATION PARAMETERS OBTAINED FOR THE GAP DISTANCE OF 6 MM.

V[0] (V)	τ1 (ns)	τ2 (ns)	τ3 (ns)	τd1 (µs)	τd2 (ns)	c1 (Ms)	c2 (ns)	σ1 (nS)	σ2 (µS)	Ec1 (kV/m)	Ec2 (MV/m)	m (ns)
6486	4.00	25.0	3.30	11.0	60.0	10.0	10.0	650.0	2.10	967.0	32.8	4.56
7048	3.45	22.5	3.10	15.0	60.0	10.0	10.0	875.0	2.50	967.0	35.6	4.56
7408	2.95	19.0	2.80	18.0	60.0	10.0	10.0	950.0	2.90	967.0	37.4	4.56
7778	2.70	18.5	2.55	20.0	60.0	10.0	10.0	1200.0	3.15	967.0	39.3	4.56
8323	1.70	15.0	2.30	21.0	60.0	10.0	10.0	1300.0	3.57	967.0	42.0	4.56

TABLE VIII
OPTIMIZED IONIZATION PARAMETERS OBTAINED FOR THE GAP DISTANCE OF 7 MM.

V[0] (V)	τ1 (ns)	τ2 (ns)	τ3 (ns)	τd1 (µs)	τd2 (ns)	c1 (Ms)	c2 (ns)	σ1 (nS)	σ2 (µS)	Ec1 (kV/m)	Ec2 (MV/m)	m (ns)
7180	3.80	28.50	4.20	16.60	60.0	10.0	10.0	949.92	2.70	967.0	36.30	4.56
7820	3.00	23.50	3.85	19.00	60.0	10.0	10.0	1100.0	3.20	967.0	39.50	4.56
8200	2.80	21.50	3.45	20.00	60.0	10.0	10.0	1150.0	3.45	967.0	41.40	4.56
8600	2.70	19.00	3.40	22.00	60.0	10.0	10.0	1250.0	3.60	967.0	43.40	4.56

TABLE IX
OPTIMIZED IONIZATION PARAMETERS OBTAINED FOR THE GAP DISTANCE OF 8 MM.

V[0] (V)	τ1 (ns)	τ2 (ns)	τ3 (ns)	τd1 (µs)	τd2 (ns)	c1 (Ms)	c2 (ns)	σ1 (nS)	σ2 (µS)	Ec1 (kV/m)	Ec2 (MV/m)	m (ns)
7818	3.70	29.50	5.10	15.50	60.0	10.0	10.0	800.00	2.75	967.0	39.50	4.56
8455	3.50	27.00	4.60	20.00	60.0	10.0	10.0	1000.0	3.20	967.0	42.70	4.56
8900	3.20	25.50	4.00	23.00	60.0	10.0	10.0	1250.0	3.60	967.0	44.90	4.56
9347	3.00	23.00	3.32	25.00	60.0	10.0	10.0	1400.0	3.90	967.0	47.20	4.56

Figs. 13-17 present comparisons between the simulated and experimentally obtained current waveforms for each gap distance and applied voltage. The transient current results are organized as it follows: Fig. 13(a), Fig. 13(b), Fig. 13(c), Fig. 13(d) and Fig. 13(e) show comparison of currents obtained with gap distance of 4 mm with the respective DC voltages of 4.851 kV, 5.248 kV, 5.525 kV, 5.801 kV and 6.198 kV.

Fig. 13
Comparison of experimentally obtained and simulated currents for a gap distance of 4 mm and applied DC voltages of (a) 4851 V, (b) 5248 V, (c) 5525 V, (d) 5801 V, and (e) 6198 V.

Fig. 14
Comparison of experimentally obtained and simulated currents for a gap distance of 5 mm and applied DC voltages of (a) 6025 V, (b) 6178 V, (c) 6510 V, (d) 6816 V, and (e) 7314 V.

Fig. 15
Comparison of experimentally obtained and simulated currents for a gap distance of 6 mm and applied DC voltages of (a) 6486 V, (b) 7048 V, (c) 7408 V, (d) 7778 V, and (e) 8323 V.

Fig. 16
Comparison of experimentally obtained and simulated currents for a gap distance of 7 mm and applied DC voltages of (a) 7180 V, (b) 7820 V, (c) 8200 V, and (d) 8600 V.

Fig. 14(a), Fig. 14(b), Fig. 14(c), Fig. 14(d) and Fig. 14(e) were obtained with the 5 mm gap distance with DC voltages of 6.025 kV, 6.178 kV, 6.510 kV, 6.816 kV and 7.314 kV; Fig. 15(a), Fig. 15(b), Fig. 15(c), Fig. 15(d) and Fig. 15(e) show numerical and experimental currents calculated and measured with the gap distance of 6 mm by applying the DC voltages of 6.486 kV, 7.048 kV, 7.408 kV, 7.778 kV and 8.323 kV, respectively; Fig. 16(a), Fig. 16(b), Fig. 16(c) and Fig. 16(d) bring comparisons of FDTD and experimental transient currents obtained by employing the gap distance of 7 mm and the respective voltages of 7.18 kV, 7.82 kV, 8.2 kV and 8.6 kV; and, finally, in Fig. 17(a), Fig. 17(b), Fig. 17(c) and Fig. 17(d) we compare numerical and experimental transient currents obtained with 7.818 kV, 8.455 kV, 8.9 kV, and 9.347 kV, respectively, by setting electrodes apart by 8 mm.

Fig. 17
Comparison of experimentally obtained and simulated currents for a gap distance of 8 mm and applied DC voltages of (a) 7818 V, (b) 8455 V, (c) 8900 V, and (d) 9347 V.

A general analysis of the figures reveals that, in agreement, both experimental and numerical peak currents tend to increase with increasing applied voltage for a given gap distance. Similarly, for a fixed voltage, a smaller gap distance generally leads to higher peak currents. This behavior is consistent with the physics of partial discharges, where higher electric fields (due to higher voltages or smaller gaps) result in more intense ionization and consequently larger discharge currents.

From Tables V-IX and from Figs. 13-17, we see that τ₁, τ₂ and τ₃ tend to be reduced as voltage increases, which is expected since the higher the voltages are, the faster tend to be the ionization processes. On the other hand, τ_d1 tend to increase with voltage, demonstrating that, as voltage increases, deionization tend to last longer. Since ionization levels increase with voltage, naturally the number of free charges that need to reattach increase, requiring more time on the deionization process as a consequence. As also one would expect, σ₁ and σ₂ tend to increase with voltage.

The obtained results demonstrate good agreement between the numerical model results and the experimental measurements, particularly in capturing the peak current and the overall waveform shape. This agreement highlights the effectiveness of the proposed 1D transmission line model and the conductivity update algorithm in replicating the essential characteristics of PD currents. However, some small discrepancies between the simulated and experimental results are observed, particularly in the rising time of the current pulse and the oscillations during the deionization phase. Those differences can be attributed to the limitations of the 1D model, which at the present time cannot fully capture the three-dimensional nature of the discharge process, including phenomena such as electromagnetic coupling, streamer branching and radial expansion. Those limitations can be addressed and possibly overcome in further research.

Finally, Figs. 18, 19 and 20 show the effective conductivities obtained for the plasma channel for the gaps measuring 4 mm, 6 mm and 8 mm, for each applied voltage, respectively. As expected, as voltage increases ionization levels rise, as calculated peak conductivities show for any given gap distance. Moreover, ionization conductivities strongly diminish from the needle (i = 1) to the plate (i = i_m). For voltages on the same level of magnitude, we see in Figs. 18-20 that by increasing the gap distance, since electric field is distributed across larger space, its local magnitudes reduce and, as a consequence, conductivity also diminishes (for instance, see Figs. 18(e) and 19(a) and Figs. 19(e) and 20(b)).

Fig. 18
Numerically obtained effective conductivities for gap distance of 4 mm for the applied voltages: (a) 4851 V, (b) 5248 V, (c) 5525 V, (d) 5801 V, and (e) 6198 V.

Fig. 19
Numerically obtained effective conductivities for gap distance of 6 mm for the applied voltages: (a) 6486 V, (b) 7048 V, (c) 7408 V, (d) 7778 V, and (e) 8323 V.

Fig. 20
Numerically obtained effective conductivities for gap distance of 8 mm for the applied voltages: (a) 7818 V, (b) 8455 V, (c) 8900 V, and (d) 9347 V.

VIII. CONCLUSION

In this work, we presented a numerical model for simulating partial discharges in air, excited by DC voltage, using a one-dimensional transmission line representation based on the telegraph equations solved with the finite-difference time-domain method. The model incorporates a comprehensive conductivity update algorithm that simulates the different stages of air ionization, including pre-ionization, streamer formation, breakdown streamer propagation, and deionization.

The model’s accuracy was validated against experimental data obtained in this work from a needleplane electrode configuration, specifically a steel needle (high-voltage electrode) and a copper plane (ground), for various gap distances and applied voltages, where effective electrical conductivity was calculated as a function of these parameters. The laboratory experiments were conducted under controlled atmospheric conditions, with consistent relative humidity levels and temperature, ensuring repeatability and minimizing environmental variability in the measured discharge current pulses. The simulation results demonstrated good agreement with the experimental measurements, particularly in capturing the peak current and the overall waveform shape, indicating the effectiveness of the proposed 1D transmission line model and the conductivity update algorithm in replicating the essential characteristics of PDs.

Despite its inherent limitations, the proposed one-dimensional model offers a computationally efficient approach to simulating PDs compared to more complex three-dimensional models. Typically, our model requires up to two minutes of processing time on a typical single computer core and about 50 MB of RAM, while 3D models often require several hours under similar conditions. For instance, in the work [²²], by using eight cores of a 64-bit 3.7 GHz processor running the Linux operating system, our FDTD-3D simulator, written in the programming language C, requires approximately two hours to complete a single PD simulation by employing 16 processing threads and requiring 4112 MB of RAM. This advantage of the proposed method makes it a valuable tool for preliminary investigations, parametric studies and developing more general PD conductivity models.

A possible application is the use of PD current waveforms as a source for generating 3D models of electric fields and charge distributions within insulation systems. By including the transient characteristics of PD currents into spatially resolved models, engineers can visualize and analyze the complex interactions between electric fields and insulating materials, leading to optimized designs for enhanced dielectric performance and reliability.

Other geometries and PD sources can also be represented by the proposed model, such as stator bar PDs or transformer PDs. The ionization parameters can be determined for those ends. Additionally, PD current waveforms or ionization parameters can be employed in the development of advanced machine learning algorithms for predictive maintenance and fault detection in high-voltage systems.

While the 1D transmission line model provides valuable insights into partial discharge behavior, future work can also be directed toward extending the model to incorporate three-dimensional effects, like electromagnetic coupling, and further enhance its accuracy in predicting the dynamic behavior of PDs in more complex scenarios, i.e., our 1D model may be limited in scenarios involving strong electromagnetic coupling with surrounding objects or ionizing fields from nearby devices. These complex interactions would require more advanced modeling approaches to possibly achieve 3D-equivalent coupling results.

Finally, our TL-FDTD model for partial discharges is adaptable to other environmental conditions, as ionization parameters can be recalculated to account for changes in temperature and humidity. Future work can focus on providing experimental data that detail the effects of these factors and recalculating the model’s parameters, enabling the development of even more general PD conductivity models based on first principles to obtain effective conductivity for diverse conditions.

REFERENCES

• ^[1] A. Haddad and D. F. Warne, Eds., Advances in High Voltage Engineering, ser. Energy Engineering. Stevenage, England: Institution of Engineering and Technology, 2004.
• ^[2] A. Gavrilovic, “32 - HVDC,” in Electrical Engineer’s Reference Book (Sixteenth Edition), sixteenth edition ed., M. Laughton and D. Warne, Eds. Oxford: Newnes, 2003, pp. 32-46, DOI: 10.1016/B978-075064637-6/50032-0.
  » https://doi.org/10.1016/B978-075064637-6/50032-0.
• ^[3] J. Guo, Z. Zheng, and A. Caprara, “Partial Discharge Tests in DC Applications: A Review,” in 2020 IEEE Electrical Insulation Conference (EIC), pp. 225-229, 2020, DOI: 10.1109/EIC47619.2020.9158747.
  » https://doi.org/10.1109/EIC47619.2020.9158747.
• ^[4] G. C. Stone, A. Cavallini, G. Behrmann, and C. A. Serafino, Practical partial discharge measurement on electrical equipment New York, NY: Wiley-IEEE Press, 2023.
• ^[5] S. Seitz, T. Gotz, C. Lindenberg, R. Tetzlaff, and S. Schlegel, “Towards Generalizable Classification of Partial Discharges in Gas-Insulated HVDC Systems using Neural Networks: Protrusions and Particles,” IEEE Transactions on Power Delivery, pp. 1-9, 2024, DOI: 10.1109/TPWRD.2024.3369872.
  » https://doi.org/10.1109/TPWRD.2024.3369872.
• ^[6] O. Eichwald, O. Ducasse, D. Dubois, A. Abahazem, N. Merbahi, M. Benhenni, and M. Yousfi, “Experimental analysis and modelling of positive streamer in air: towards an estimation of O and N radical production,” Journal of Physics D: Applied Physics, vol. 41, no. 23, pp. 1-11, 2008, DOI: 10.1088/0022-3727/41/23/234002.
  » https://doi.org/10.1088/0022-3727/41/23/234002.
• ^[7] N. Merbahi, A. Abahazem, D. Dubois, O. Eichwald, and M. Yousfi, “Optical and electrical analyses of DC positive corona discharge in N₂/O₂/CO₂ gas mixtures,” The European Physical Journal Applied Physics, vol. 42, no. 1, pp. 55-61, 2008, DOI: 10.1051/epjap:2008035.
  » https://doi.org/10.1051/epjap:2008035.
• ^[8] N. Hozumi, T. Okamoto, and T. Imajo, “Discrimination of partial discharge patterns using a neural network,” IEEE Transactions on Electrical Insulation, vol. 27, no. 3, pp. 550-556, 1992, DOI: 10.1109/14.142718.
  » https://doi.org/10.1109/14.142718.
• ^[9] T. Hoshino, S. Maruyama, and T. Sakakibara, “Simulation of propagating electromagnetic wave due to partial discharge in GIS using FDTD,” IEEE transactions on power delivery, vol. 24, no. 1, pp. 153-159, 2008, DOI: 10.1109/CMD.2008.4580205.
  » https://doi.org/10.1109/CMD.2008.4580205.
• ^[10] R. M. S. Oliveira, J. F. M. Modesto, V. Dmitriev, F. S. Brasil, and P. R. M. Vilhena, “Spectral Method for Localization of Multiple Partial Discharges in Dielectric Insulation of Hydro-Generator Coils: Simulation and Experimental Results,” Journal of Microwaves, Optoelectronics and Electromagnetic Applications, vol. 15, pp. 170 - 190, 2016, DOI: 10.1590/2179-10742016v15i3592.
  » https://doi.org/10.1590/2179-10742016v15i3592.
• ^[11] R. Morrow and N. Sato, “The discharge current induced by the motion of charged particles in time-dependent electric fields; Sato’s equation extended,” Journal of Physics D: Applied Physics, vol. 32, no. 5, p. L20, mar 1999, DOI: 10.1088/0022-3727/32/5/005.
  » https://doi.org/10.1088/0022-3727/32/5/005.
• ^[12] N. Sato, “Discharge current induced by the motion of charged particles,” Journal of Physics D: Applied Physics, vol. 13, no. 1, p. L3, sep 1980, DOI: 10.1088/0022-3727/13/1/002.
  » https://doi.org/10.1088/0022-3727/13/1/002.
• ^[13] L. V. M. Fabris and J. C. C. da Silva, “Simulation of current pulses and sound waves resulting from partial discharges in a needle-plane geometry in air,” Journal of Microwaves, Optoelectronics and Electromagnetic Applications, vol. 21, no. 4, p. 27, dec 2022, DOI: 10.1590/2179-10742022v21i4263644.
  » https://doi.org/10.1590/2179-10742022v21i4263644.
• ^[14] M. Talaat, A. El-Zein, and A. Samir, “Numerical and simulation model of the streamer inception at atmospheric pressure under the effect of a non-uniform electric field,” Vacuum, vol. 160, pp. 197-204, 2019, DOI: 10.1016/j.vacuum.2018.11.037.
  » https://doi.org/10.1016/j.vacuum.2018.11.037.
• ^[15] D. Raouti, S. Flazi, and D. Benyoucef, “Modeling and identification of electrical parameters of positive dc point-to-plane corona discharge in dry air using RLS method,” IEEE Transactions on Plasma Science, vol. 44, no. 7, pp. 1144-1149, 2016, DOI: 10.1109/TPS.2016.2577634.
  » https://doi.org/10.1109/TPS.2016.2577634.
• ^[16] F. Trauble, S. T. Millmore, and N. Nikiforakis, “An improved equation of state for air plasma simulations,” Physics of Fluids, vol. 33, no. 3, p. 036112, 03 2021, DOI: 10.1063/5.0044008.
  » https://doi.org/10.1063/5.0044008.
• ^[17] A. Loubani, N. Harid, H. Griffiths, and B. Barkat, “Simulation of Partial Discharge Induced EM Waves Using FDTD Method - A Parametric Study,” Energies, vol. 12, no. 17, 2019, DOI: 10.3390/en12173364.
  » https://doi.org/10.3390/en12173364.
• ^[18] J. D. Kraus, Electromagnetics, 3rd ed. McGraw-Hill, 1984.
• ^[19] A. Taflove and S. C. Hagness, Computational electrodynamics: the finite-difference time-domain method Artech house, 2005.
• ^[20] R. Sigmond, “The residual streamer channel: Return strokes and secondary streamers,” Journal of applied physics, vol. 56, no. 5, pp. 1355-1370, 1984, DOI: 10.1063/1.334126.
  » https://doi.org/10.1063/1.334126.
• ^[21] E. Seran, M. Godefroy, E. Pili, N. Michielsen, and S. Bondiguel, “What we can learn from measurements of air electric conductivity in ²²²Rn-rich atmosphere,” Earth and Space Science, vol. 4, no. 2, pp. 91-106, 2017, DOI: 10.1002/2016EA000241.
  » https://doi.org/10.1002/2016EA000241.
• ^[22] R. M. S. Oliveira, J. S. Nascimento, D. M. Fujiyoshi, T. S. Lima, and A. J. C. Sena, “A finite-difference timedomain formulation for modeling air ionization breakdown streamers,” Journal of Microwaves, Optoelectronics and Electromagnetic Applications, vol. 21, no. 3, pp. 427-444, 2022, DOI: 10.1590/2179-10742022v21i3259333.
  » https://doi.org/10.1590/2179-10742022v21i3259333.
• ^[23] C. R. Paul, Introduction to Electromagnetic Compatibility Germany: Wiley, 2006.
• ^[24] R. M. S. Oliveira and D. M. Fujiyoshi, “Finite-difference time-domain modeling of multi-stage soil ionization with residual resistivities - Part I: Theoretical background and the proposed FDTD formulation,” Electric Power Systems Research, vol. 184, pp. 1-10, 2020, DOI: 10.1016/j.epsr.2020.106300.
  » https://doi.org/10.1016/j.epsr.2020.106300.
• ^[25] A. Liew and M. Darveniza, “Dynamic model of impulse characteristics of concentrated earths,” in Proceedings of the Institution of electrical Engineers, vol. 121, no. 2, pp. 123-135, 1974, DOI: 10.1049/piee.1974.0022.
  » https://doi.org/10.1049/piee.1974.0022.
• ^[26] R. Courant, K. Friedrichs, and H. Lewy, “On the partial difference equations of mathematical physics,” IBM journal of Research and Development, vol. 11, no. 2, pp. 215-234, 1967, DOI: 10.1147/rd.112.0215.
  » https://doi.org/10.1147/rd.112.0215.
• ^[27] F. W. Grover, Inductance calculations: working formulas and tables, Special ed. Instrument Society of America, 1973.
• ^[28] J. A. Nelder and R. Mead, “A simplex method for function minimization,” The Computer Journal, vol. 7, no. 4, pp. 308-313, 1965, DOI:10.1093/comjnl/7.4.308.
  » https://doi.org/10.1093/comjnl/7.4.308.

Publication Dates

• Publication in this collection
  03 Feb 2025
• Date of issue
  2025

History

• Received
  22 June 2024
• Reviewed
  24 Sept 2024
• Accepted
  11 Dec 2024