Singlet oxygen reactivity in water-rich solvent mixtures

Abstract

The 3-methylindole (3MI) oxygenation sensitized by psoralen (PSO) has been investigated in 100%, 20% and 5% O2-saturated water/dioxane (H2O/Dx) mixtures. The lowering of the ¹O2* chemical rate when water (k chem∆3MI = 1.4 × 109 M-1 s-1) is replaced by deuterated water (k chem∆3MI = 1.9 × 108 M-1 s-1) suggests that hydrogen abstraction is involved in the rate determining step. A high dependence of the chemical rate constant on water concentration in H2O/Dx mixtures was found showing that water molecules are absolutely essential for the success of the 3MI substrate oxidation by ¹O2* in water-rich solvent mixtures.

singlet oxygen; psoralen; solvent effects

ARTIGO

Singlet oxygen reactivity in water-rich solvent mixtures

Cristina Sousa^I; Ana Maria Botelho do Rego^II; Teresa Sá e Melo^{II, *}

^IDepartamento de Química, Universidade de Évora, Largo dos Colegiais 2, 7000 Évora, Portugal

^IICentro de Química-Física Molecular, Instituto Superior Técnico, Universidade Técnica de Lisboa, 1049-001 Lisboa, Portugal

ABSTRACT

The 3-methylindole (3MI) oxygenation sensitized by psoralen (PSO) has been investigated in 100%, 20% and 5% O₂-saturated water/dioxane (H₂O/Dx) mixtures. The lowering of the ¹O₂^* chemical rate when water (k_chem∆^3MI = 1.4 × 109 M^-1 s^-1) is replaced by deuterated water (k_chem∆^3MI = 1.9 × 108 M^-1 s^-1) suggests that hydrogen abstraction is involved in the rate determining step. A high dependence of the chemical rate constant on water concentration in H₂O/Dx mixtures was found showing that water molecules are absolutely essential for the success of the 3MI substrate oxidation by ¹O₂^* in water-rich solvent mixtures.

Keywords: singlet oxygen; psoralen; solvent effects.

INTRODUCTION

Photosensitized reactions induced in biological substrates such as proteins or enzymes, and the characterization of the peroxide photoproducts,¹ after absorption of light by drugs (antibiotics, dyes and psoralens) are important to assess drugs phototoxicity.² To clarify the mechanism of substrate photodegradation induced by a photosensitizer like psoralen (PSO), it is important to characterize the transient species formed after PSO excitation through its photophysical parameters.

Due to the very short singlet excited state, lifetimes of psoralen (PSO, the parent compound), in water/dioxane mixtures < 1 ns, the photoinduced chemical reaction will occur from PSO triplet state. Moreover, triplet state produces singlet oxygen (¹O₂^*) by energy transfer, which can in turn react with substrates by type II photodynamic mechanism.³

In a previous work we have determined the PSO triplet lifetimes (τ_T) and quantum yields (Φ_T), in water/dioxane mixtures (H₂O/Dx) and in a set of 16 organic solvents.⁴ We have reported that triplet formation quantum yield, Φ_T, of PSO is a linear function of water concentration in H₂O/Dx solvent mixtures, increasing from 0.033 in Dx to 0.495 in water.⁴ These major changes in triplet yield with media are an important factor for the efficiency of light-induced cell killing, as expected for a mechanism based on intermediate generation of singlet molecular oxygen.

On the other hand, it is well-known that the lifetimes (τ_∆) of the near-IR emission of ¹O₂^*, detected at 1270 nm, show an enormous solvent dependence,⁵ varying from ~3.5 µs in water to 68 µs in deuterated water.⁶ In addition, the ¹O₂^* luminescence quantum yield, Φ_P, in water is very low (6.5 × 10^-7) whereas in deuterated water it is 19 times greater.⁷ One way or other, the observed ¹O₂^* quenching by substrate whether via energy transfer, charge transfer or chemical reaction is always additive to the quenching by the solvent. Particularly, this is the case in hydroxylic solvents with abstractable hydrogen atoms.⁸ The bimolecular character of τ_∆ quenching by the solvent, firstly reported by M. Rodgers,⁹ is clearly observed in (H,D)₂O/Dx solvent mixtures.¹⁰ We found (see Appendix) that those reported data in (H,D)₂O/Dx (10) can be fitted (R²= 0.9976) to the Equations:

where k_Dx, = 3665 M^-1 s^-1, k_H2O = 3887 M^-1 s^-1 and k_D2O = 275 M^-1 s^-1 are the bimolecular rate constants, k₀ = 2.3 × 10^-4 s^-1 is the spontaneous emission of isolated ¹O₂^* molecules and [Dx], [H₂O] or [D₂O] are the molar concentration of the solvents.

Thus, the direct determination of ¹O₂^* emission quenching (k_Q^∆ = k_phys^∆ + k_chem^∆) by substrates, in water solution (where intrinsic Φ_P= 6.5 × 10^-7 and 1/τ_∆ = 1/3.5 µs^-1, as stated above), is very difficult and poorly documented in literature. For that very reason, some authors recommend to use D₂O to perform studies in water⁸ although, as it is shown here, results cannot be extrapolated to H₂O case.

For the above reasons, the overall ¹O₂^* quenching by biological targets reported in literature are always determined in solvents for which ¹O₂^* intrinsic lifetime (and emission intensity) are high enough to be accurately measured. For instance, in deuterated water τ_∆ = 68 µs, in Dx τ_∆ = 27 µs, in MeCN τ_∆ = 58 µs, in EtOH τ_∆ = 13 µs, and in a mixture of both, 1:1 v/v D₂O/EtOH, τ_∆ = 21 µs.^5,11 In those solvents, the ¹O₂^* overall quenching with a good oxidable substrate such as 3-methylindole (3MI) has been reported with rate constants, k_Q^∆, of 1.6 × 10⁸ M^-1 s^-1 in 1:1 v/v D₂O/EtOH¹¹, 3.2 × 10⁸ M^-1 s^-1 in D₂O¹³, 6.8 × 10⁷ M^-1 s^-1 in MeCN¹² and 5.6 × 10⁷ M^-1 s^-1 in Dx.¹² The chemical part, k_chem∆^3MI ,of the ¹O₂^* quenching by 3MI has values of 1.20 × 10⁸ M^-1 s^-1 in 1:1 v/v D₂O/EtOH,¹¹ 1.34 × 10⁸ M^-1 s^-1 in D₂O,¹² 2.3 × 10⁶ M^-1 s^-1 in MeCN,^11,13 and < 1.0 × 10⁶ M^-1 s^-1 in Dx. (this work). It can be observed that k_{chem 8710;}^3MI / k_phys∆^3MI ratio increases with increasing hydroxylic character of the solvent and its number of abstractable H atoms.

As described above, the overall ¹O₂^* quenching by substrate (k_Q∆^3MI = k_phys∆^3MI + k_chem∆^3MI) is very difficult to be determined in water solution. On the other hand, the chemical part of this rate (k_chem∆^3MI) can only be measured by steady state irradiation experiments, regardless the solvent used. These values are very time-consuming and some authors claimed they are difficult to obtain.¹⁴ Unfortunately, the most recent reviews on the subject are only concerned with the physical part of the ¹O₂^* deactivation processes.⁷

Due to the lack of experimental data, the role of water molecules on the ¹O₂^* chemical reaction with substrates is not clear. Because of the low activation energy for singlet oxidation reactions processes (0.5 - 8 kcal), there is no temperature effect on the rate of such photoreaction.¹⁵ It is claimed that solvents play no role in the chemical reaction with substrates and it will only affect the lifetime of singlet oxygen by the solvent polarity/polarizability effects.¹⁶ Moreover, these studies have additional difficulties to obtain simultaneously k_chem∆^3MI and k_Q∆^3MI values in nonpolar and highly polar solvents, due to the insolubility of the most common biological substrates in water. Nevertheless, a contrasting result has been reported for naphthalenic substrates with a 142 times increase on k_chem∆^3MI (45 times increases on k_Q∆^3MI) when going from methanol to water solutions, without any reasonable quantitative explanation.¹⁶ The crucial role of water to the [4+2] cycloaddition between ¹O₂^* and electron-rich para-alkyl phenols was also recently reported.¹⁷

Some analyses were performed in linear multi-parameter fits using solvatochromic properties providing some physical insight for the charge transfer induced ¹O₂^* quenching,^16,17 but the physical meaning of such enhancement, particularly the role of water in the chemical reactivity remains unclear.

Steady state irradiation procedure using variable concentrations of water in solvent mixtures is the only way to evidence the role of the H-atoms in the ¹O₂^* chemical quenching mechanism in aqueous solution.

The kinetics and quantum yields of PSO triplet state, as a function of water concentration in H₂O/Dx, were taken from our previous work.⁴ Since the intrinsic τ_∆ lifetimes have already been reported for the same (H,D)₂O/Dx solvent mixtures,¹⁰ it would be possible to test PSO ability to induce substrate oxidation by singlet oxygen (¹O₂^*), as a function of water concentration.

We have chosen an easily oxidizable substrate such as 3-methylindole (3MI) instead of 3-alanilindole (tryptophan, Trp) to perform a steady state irradiation of PSO. In fact, the alanine substitution increases the aqueous and non-aqueous solubility of this derivative relatively to Trp. In addition, the solvent dependent emission of the indole ring is easily detected. Moreover, methyl substitution at 3 position of the indole ring was shown to highly increase its photoreactivity.^11,14

Making use of psoralen as photosensitizer, we have accomplished a kinetic study on the decrease of 3MI substrate concentration as a function of PSO irradiation time, by changing: the water concentration in (H,D)₂O/Dx solvent mixtures and thus the PSO triplet formation quantum yields; the molecular oxygen concentration, using 5, 20 and 100% O₂-saturated solutions; the substrate (3MI) and the photosensitizer (PSO) ground state concentrations; the singlet oxygen lifetime, using dioxane solvent mixtures with water or deuterated water.

From the resulting data we extracted information about both type I and type II kinetic mechanisms, involving (3PSO* + 3MI) and (3MI + ¹O₂^*) direct pathways, respectively.

In this work we show that 3MI photodegradation induced by psoralen is highly dependent on the concentration of water molecules in the aqueous solvent mixtures.

EXPERIMENTAL

Psoralen and 3-methylindole were reagents commercially available from Sigma. Deuterium oxide was purchased from Aldrich. The solvents 1,4-dioxane (spectroscopic grade) and absolute ethanol (HPLC grade) were provided by Merck. The solvent, dioxane (and 3MI compound), came from freshly open bottles or kept frozen during storage to avoid oxidation and peroxide formation.

Pure water was obtained from deionised tap water that was first distilled and then evaporated in a quartz still. Binary solvent mixtures were prepared with water (or with sodium (di) hydrogenophosphate buffer) making the mixture volumetrically complete with dioxane. The solvents dioxane and water are miscible in all proportions. Moreover, the sensitizer PSO (10 µM) and the substrate 3MI (200 to 480 µM) are completely soluble in the solvent mixtures used.

Steady state irradiations were performed in a home-made setup using a high-pressure 200 W mercury arc lamp. The 365 nm Hg line was isolated with optical and chemical filters. Sample was bubbled with the appropriate gas (O₂, N₂ or a mixture of 5 or 20% O₂ in N₂) and submitted to magnetic stirring to avoid photoproducts damage during irradiation. Temperature was kept constant by the use of a cell-holder thermostat. The decrease in 3MI substrate concentration with irradiation time was monitored by fluorescence measurements in a SPEX Fluorolog 2. The maximum fluorescence intensity of indole derivative was monitored at 368 nm for an excitation wavelength at 310 nm. The fluorescence excitation was chosen at 310 nm because, at this wavelength, the 3MI absorption extinction coefficient is low and thus, we can make solutions with high substrate concentrations without inner filter effects (ε_G = 233 M^-1 s^-1).

The UVA irradiation at 365 nm, with a fluence rate of 11.7 mJ s^-1 determined by ferrioxalate actinometry,¹⁸ is only absorbed by PSO photosensitizer. The psoralen concentration is kept constant (10 µM), in the irradiated volume (5 mL). The PSO absorption extinction coefficient at 365 nm vary from 1100 to 1450 M^-1 cm^-1 in dioxane to water solutions, respectively.

The substrate photodegradation was monitored by the decrease in the 3MI fluorescence intensity at the maximum of its emission band, where PSO emission is absent (see Figure 1). No changes on 3MI emission band shape were observed in samples with irradiation time. In this study no attempts were made to analyze the photoproducts.

The infrared emission of ¹O₂^* was measured with a liquid nitrogen-cooled germanium photodiode detector (403HS, Edinburgh Instruments). A 355 nm Nd-YAG laser, 7 mJ intensity and 7 ns pulse width was used to excite the sensitizer (Minilite II, Continuum). The 1270 nm signal was recorded in a 12 bit transient recorder (TR1202, FastComTec) and transferred to a PC. Both IR interference filter at 1270 nm (1270BP50) and a 1000 nm cut-off filter (LL-1000-F) were used. The Ge-detector with a preamplifier, (surface area of 0.25 cm² in a sapphire window) operates at a bias of -300 V, supplied by a HV power supply (PS3, Edinburgh Instruments). Aqueous ludox scatter solutions were used to monitoring the fast decay signal due to the apparatus function. Both unwanted signals, i.e, the fundamental at 1064 nm from the laser excitation and the fluorescence from NIR filters, were eliminated by putting a filter (% T = 0.08 at 1064 nm), on the laser excitation beam. However this operation decreases by 28% the 355 nm laser excitation energy. For this reason we used ZnTPP instead of PSO because a factor of 4 was found on relative Φ_∆ values obtained from optically matched solutions. The quenching of ¹O₂^* decay by increased 3MI concentrations were determined in air-saturated toluene solutions, using the synthetic 5,10,15,20 tetraphenyl-21H,23H-porphin, zinc (ZnTPP). The ¹O₂^* quenching rate by 3MI in D₂O solutions was already reported in literature, where TPP or methylene blue were employed as sensitizers.¹²

The time profiles of the PSO triplet-triplet absorption were determined by the third harmonic excitation light (355 nm) of a Nd:YAG laser from a Spectra Physics time-resolved flash photolysis equipment. Solutions were prepared by bubbling N₂ followed by vacuum degassing. Samples were monitored at the maximum of T-T absorbance at 450 nm. The overall rate constants, k_Q^3MI = k_phys^3MI + k_chem^3MI, (see Scheme 1) of PSO triplet state quenching by 3MI substrate molecules in degassed solutions, were used in aerobic conditions for the kinetic analysis.

The 3MI photodegradation rates (–d[3MI]/dt) were measured by fluorescence as a function of UVA irradiation time, in different oxygen saturated (H,D)₂O/Dx mixtures.

The chemical rate constants of PSO triplet reaction with 3MI (k_chem^3MI) were measured by steady-state irradiation procedure, in the absence of molecular oxygen.

Singlet oxygen lifetime values (τ_∆) in water (and deuterated water) (H,D)₂O/Dx mixtures were taken from the literature.¹⁰ The overall quenching rate constants of ¹O₂* by 3MI in D₂O (3.2 10⁸ M^-1 s^-1) and in Dx (5.6 10⁷ M^-1 s^-1) were taken from literature¹² and used for kinetic calculations. The molecular oxygen concentration in the different solvent mixtures was determined assuming a linear additivity of the molecular oxygen solubilities, in dioxane (7.55 mM) and in water (1.325 mM), for oxygen saturated solutions.^18,19 Water molar concentration ranged from 28 M (50% v/v) to 50 M (90% v/v) in the solvent mixtures were used in this work.

RESULTS

Figures 1 and 2 show ground state absorption and fluorescence spectra of 3MI substrate and PSO photosensitizer, in H₂O/Dx mixture (with 90% v/v water). It can be observed that the 365 nm UVA irradiation light can only be absorbed by the photosensitizer, PSO.

Since the half width of the fluorescence band of the indole derivative is unchanged with irradiation time, we assumed that photoproducts were not fluorescent at the monitored 3MI emission wavelength. Moreover, the fluorescence intensity monitored at 368 nm belongs only to 3MI emission since at this wavelength the PSO fluorescence signal is negligible, being 10³ lower than that of the indole derivative (Figure 1).

Triplet quenching of PSO molecules by 3MI substrate was studied by flash photolysis in degassed solutions. It was verified that the PSO triplet formation quantum yield, Φ_T, was unchanged by the isotopic substitution when water is replaced by deuterated water, in the solvent mixtures.

The lifetime of PSO triplet excited state is concentration dependent. Its triplet decay rate constant decreases linearly with increasing ground state concentration, denoting a rapid self-quenching reaction (k_sq^T = 1.5×10⁹ M^-1 s^-1), in H₂O/Dx mixtures.⁴ For all psoralen derivatives, the observed triplet self-quenching rates have nearly diffusion limited values, but the exact nature of this excited-state association is unknown.

The reciprocal of the observed PSO triplet lifetime plotted as a function of the 3MI substrate concentrations were determined by laser flash photolysis. The observed rate constant is given by Equation 3:

where (k₀^T + k_sq^T[PSO]) and k_Q^T are the reciprocal of the observed PSO triplet lifetimes in the absence and in the presence of 3MI substrate, respectively.

The values for the sum (k₀^T + k_sq^T [PSO]) of (3.6 ± 0.6) × 10⁵ s^-1 and (3.1 ± 0.1) × 10⁵ s^-1 were obtained in 90% v/v H₂O and D₂O in dioxane, respectively. These results compare with those obtained for PSO triplet self quenching in water²⁰ and in ethano.^l2

The overall triplet quenching by 3MI, is the sum of both physical and chemical pathways (k_Q^3MI = k_phys^3MI + k_chem^3MI), as shown in Scheme 1 (c + d processes). The flash photolysis determination of PSO triplet quenching, k_Q^3MI =(3.60 ± 0.4) × 10⁹ M^-1 s^-1 and (3.37 ± 0.08) × 10⁹ M^-1 s^-1, were obtained in 90% v/v H₂O and D₂O in dioxane, respectively. These values are of the same order of magnitude of those already reported in water, for PSO triplet quenching by tryptophan.²⁰

The kinetics of 3MI photoreaction was studied by steady state irradiation procedure.

The transient species formed after PSO excitation and the deactivation pathways are shown in the Scheme 1.

After the absorption of a photon by ground state PSO, the obtained singlet excited state (¹PSO*) readily decays to ground state or to triplet state (³PSO*). The differential equation that describes the 3MI concentration decrease with irradiation time, assuming that the concentration of products is equal to the concentration of 3MI disappearing, is given by:

And

where d[3MI]/dt is the experimental rate of 3MI degradation and rate constants are defined in Scheme I.

The solution of Equations 4 and 5 together does not yield an analytical function of [3MI] vs time. The classical approach to overcome this problem is to assume steady state conditions for the transient species, i.e., d[³PSO*]/dt=0. Doing so, the reaction rate, v_N2 is given by the differential Equation 6, where N₂ stands for nitrogen-saturated solution.

where I_abs is the PSO absorption intensity, V is the volume of irradiated solution, Φ_T is the triplet formation quantum yield and t the irradiation time. Since the observed decrease of 3MI concentration with the irradiation time is always exponential, it means that [3MI] should appear just in the numerator of Eq. 6. This is only true if k_Q^3MI≈ k_Q^prod, Equation 6 becoming:

Since the k₀^T, + k_sq^T and k_Q^3MI were previously determined in 90 % v/v H₂O and D₂O in dioxane (see above), the only parameter needed to fit Equation 7 to experimental data is k_chem^3MI. From the fitting, values of (2.39 ± 0.2) × 10⁸ M^-1 s^-1 and (9.07 ± 0.5) × 10⁸ M^-1 s^-1 were determined for the chemical rate constant k_chem^3MI, in normal and deuterated water (90%v/v), respectively, in nitrogen-saturated solutions. Moreover, in deuterated water, the use of different PSO concentrations leads to the same k_chem^3MI values. Therefore, in D₂O, an invariant value for the chemical rate constant, k_chem^3MI was assumed.

In the absence of molecular oxygen the indole derivative, 3MI, can easily react by electron transfer to triplet PSO to yield ion radicals (Type I pathway). The formation of neutral tryptophan TrpH and PSO^.- anion have already been described.²¹ In deuterated water, the hydrated electrons, which react rapidly with PSO (k ~ 10¹⁰ M^-1 s^-1), is expected to be more stabilized than in normal water.²² This may be the reason for having k_Q^3MI(D₂O)> k_Q^3MI (H₂O).

As described above, the values of the overall triplet quenching rate constants k_Q^3MI (= k_phys^3MI + k_chem^3MI), were determined by laser flash photolysis. Thus, the difference k_phys^3MI = k_Q^3MI–k_chem^3MI can be obtained as shown in Table 1.

It can be observed that, in the absence of molecular oxygen, the triplet quenching by 3MI is mainly due to a physical process rather than to a chemical one. The major physical deactivation is a diffusion controlled process with values of the same order of magnitude of those reported for PSO triplet quenching by indole derivatives.²⁰

The kinetics of 3MI photooxygenation was studied by steady state irradiation in the presence of three concentrations of oxygen (5, 20, 100%) for each solution. The pathway (Type II), concerning the energy transfer from PSO triplet state to ³O₂ ground state, is operative in the presence of oxygen yielding singlet oxygen ¹O₂*. The classical kinetic mechanism³ is shown below, in Scheme 2.

Summing all the pathways, the 3MI photodegradation rate is given by:

Once again, since the experimental data, I_f(t) ∝ [3MI] (t), is a monoexponential function, the steady-state assumption for transient species can be used and Equation 9 is obtained:

where k_O2^T is the bimolecular energy transfer rate constant from PSO triplet to ground state ³O₂ oxygen and k_∆ is the reciprocal of singlet oxygen lifetime. Constants are defined in Scheme 2. Also, since the decay is monoexponential, it means that k_Q^3MI≈ k_Q^prod and k_Q∆^3MI≈ k_Q∆^prod k_Q being the sum of the physical and chemical rate constants. Equation 9 can, therefore, be rewritten as:

There are now just three parameters needed to fit Equation 10 to data: , 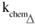^3MI and, ^prod since all the other ones were already known from experiments in the absence of oxygen and the singlet oxygen intrinsic lifetimes in (H,D)₂O/Dx mixtures were taken from literature.⁶ Data treatment has shown that the goodness of the fitting is not very sensitive to the value of k_O2^T and we assumed a value of 3×10⁹ M^-1 s^-1, the same order of magnitude as the rate of energy transfer of derivatives (8-methoxypsoralen, 3-carbethoxypsoralen, etc) triplet state to molecular oxygen, in water solutions.

In order to increase the ratio between the number of experimental points and the number of fitted parameters, values for each solvent composition (and different oxygen concentrations) were fitted together. Correlation coefficients obtained range from 0.9 to 0.999. The experimental data and the fitted curves are shown in Figures 3 and 4, for three different O₂ concentrations in solvent mixtures with different water (or deuterated water) contents.

The assumed rate constant value ( = 3 × 10⁹ M^-1 s^-1) is the value needed in order to obtain ^3MI of the order of magnitude of the reported one in D₂O (^3MI = 3.2 × 10⁸ M^-1 s^-1).⁹ Moreover, the fitted value is independent of the solvent polarity, as expected for triplet energy transfer processes from carbonyl molecules to triplet molecular oxygen.^10,13

In this way, the unknown rate constants (

^3MI and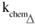 ^3MI) were obtained by fitting as shown in Figures 3 and 4. No fitting was possible using fixed values of k_chem^∆. A large variation of both k_Q^∆ and k_chem^∆ with water content was obtained. All the rate constants present in the kinetic Scheme 2 are listed in Table 2.

The overall quenching (physical + chemical) of the ¹O₂ ^* by 3MI molecules was monitored by direct ¹O₂ ^* luminescence decay at 1270 nm. Figure 5 shows the time-resolved luminescence decays from optically matched ZnTPP and PSO in air-saturated toluene solutions. The laser beam was filtered to avoid the fundamental of the Nd-YAG at 1064 nm and the fluorescence of NIR filters which results in lowering ~28% of the 355 nm laser excitation. With the temporal resolution of our equipment it was impossible to observe the ¹O₂ ^* quenching by 3MI in water solution since τ_∆ << 3.5 µs when 3MI is added. The ¹O₂^* quenching by 3MI was determined in air-saturated toluene ([O₂] = 1.74 mM), using ZnTPP as sensitizer. As shown in Figure 5 insert, a quenching rate constant with a value of k_∆^total = 1 x 10⁷ M^-1 s^-1 was obtained in agreement with literature value.¹³

DISCUSSION

The changing of rate constants with solvent properties (polarizability/polarity, acidity and basicity index and Hildebrand cavity of solvents) are usually analysed through the well-known Kamlet/Taft's and Hildebrandt solvatochromic parameters. The correlation obtained between the logarithm of a given rate constant with those solvent empirical parameters is indicative of the mechanism nature of the process characterized by that constant rate. Since in a water/dioxane mixture, several parameters change, one way of trying to rationalize the experimental

^3MI and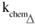 ^3MI values is to fit them to the empirical π*, α, β and δH parameters of the solvent mixture. The following Equation 11 was used for that:

π*, α, β and δH being the solvent polarizability/polarity, the acidity and basicity index and the Hildebrand cavity, respectively and s, a, b and h its relative weight.

The π*, α, β parameters of water/dioxane mixtures used in the fitting were computed from an empirical polarity scale derived from the triplet quantum yields (Φ_T) of psoralen (PSO)⁴ and derivatives, 8-methoxypsoralen (8MOP) and 5-methoxypsoralen (5MOP)²³ in a wide range of 16 pure organic solvents and a set of aqueous solvent mixtures. By taking the indicator dye 7-amino, 4-methylcoumarin (coumarin 120), whose molecular structure is closer to our furocoumarins than the commonly used E_T(30) of betaine dye, an empirical scale for psoralen E_T(PSO) was derived in order to get the correlations between the reported scale E_T(120) = 26.71–2.02 π* - 1.58 α -1.32 β (10³ cm^-1)²⁴ and the Φ_T of PSO and derivatives 8MOP and 5MOP in water/dioxane mixtures. The π*, α and β parameters, shown in Table 3, were computed in this work for the entire range (0 to 100%) of H₂O:Dx solvent mixtures through the following relationships:

-ln Φ_T (PSO) = 1.83 - 0.57π* - 0.78α - 0.11β R² = 0.999 -ln Φ_T (5MOP) = 2.74 - 2.13π* - 0.15α - 1.45β R² = 0.992 -ln Φ_T (8MOP) = 2.23 - 0.65π* - 2.19α - 0.84β R² = 0.993

The π* parameters of the mixtures are in agreement with the literature values.²⁵ The same empirical parameters were assumed for D₂O:Dx mixtures. The fitting of the total and the chemical rates to the solvent parameters of Table 3 yield h and b virtually zero:

ln

^3MI = 5.55π* + 11.44α and ln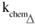 ^3MI = 5.04π* + 11.72α for D₂O:Dx mixtures

ln

^3MI = 5.84π* + 12.80α and ln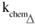 ^3MI = 5.63π* + 12.96α for H₂O:Dx mixtures

These results may be interpreted as a mechanism for the chemical reaction involving a hydrogen ion abstraction from water since the relative weight of parameter a is larger in H₂O than in D₂O. But this conclusion could be reached even without this parametric fitting since the experimental results show that 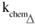^3MI (D₂O)<< 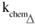^3MI (H₂O).

Another approach to rationalize the results comes from the fact that in both mixtures of Dx:H₂O and Dx:D₂O, we can write 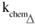^3MI∝ [(D,H)₂O]ⁿ where n >> 1 for both Dx:H₂O and Dx:D₂O.

This approach is supported by Equations 1 and 2 where variations of k_/Δ with the composition in Dx:(D,H)₂O was completely explainable by a collisional mechanism. Here, the larger variation with water concentration, expressed by n=5.2 for D₂O mixtures and n=6.1 for H₂O mixtures, suggests that the reaction between 3MI and ¹O₂^* should need a cage of a few water molecules, n being its average number.

It was already reported in the literature the role of such complexes in the substrate oxidation by singlet oxygen. Formation of such a complex is entropically unfavoured. However, a photoreaction involving 3 water molecules has been suggested to occur in cells in the presence of ¹O₂^*26 and later confirmed by other authors.²⁷ Another reaction involving 4 water molecules in photoinduced deprotonation of 7-hydroxyquinoline in acidic media has been reported in literature.²⁸ The reaction of water molecules with ¹O₂* was first described in antibody-mediated reactions in cells²⁶ and later confirmed by other authors.^29,30

To render evident the importance of the water molecules on the ¹O₂^* chemical reaction pathway, it was necessary the convergence of two factors which are present in the solvent mixtures used: singlet oxygen is highly electrophilic and thus the 3MI substrate being a good electron donor will greatly increase the substrate oxygenation,¹⁵ the optimal pH for ¹O₂^* production is approximately 9.2, which is the alkaline environment of the H₂O:Dx solvent mixtures.^15,31

CONCLUSIONS

3-Methylindole photodegradation induced by psoralen in the presence of oxygen is highly dependent on the concentration of water molecules in the aqueous solvent mixtures with dioxane.

The kinetic scheme proposed assumes that photoproducts have a quenching effect, both on ³PSO^* and on ¹O₂^*, identical to the quenching effect of 3MI. This assumption is required to explain the pseudo-first order experimentally verified. Indeed, the 3MI concentration decrease, as a function of irradiation time, always follows an exponential law, i.e., a pseudo-first order kinetics.

The physical deactivation of singlet oxygen by 3MI is negligible when compared to the reactive one. Hydrogen abstraction is involved in the rate determining step since the reaction constant

^3MI is one order of magnitude larger in H₂O/Dx than in D₂O/Dx mixtures.

Due to the magnitude of τ_∆ in water (3.5 µs) and to its lowering due to the high chemical quenching rate (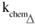^3MI > 1.4 × 10⁹ M^-1 s^-1), it was experimentally impossible to get directly the quenching rate of ¹O₂^* luminescence at 1270 nm in the presence of 3MI in water, or in water-rich solutions of the solvent mixtures.

The solvatochromic parameters analysis shows that the weight of parameter a is larger than the weight of parameter π*, the former being larger in H₂O than in D₂O. This last result confirms that an abstraction of a proton is involved in the mechanism.

Moreover, a power law is obtained when

^3MI are plotted against the water concentration: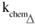 ^3MI∝[(H,D)₂O]ⁿ, n =5 to 6. This suggests that 3MI oxidation requires, besides the singlet oxygen, the simultaneous participation of a cage with an average number of n = 5 to 6 water molecules.

This important reaction pathway could explain the puzzling result of 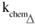and varying enormously with water concentration, which is not explainable by a direct ¹O₂* + 3MI kinetic pathway described by the classic type II molecular mechanism.

The dependence on water concentration and the water isotopic effect, can be explained by the existence of a collisional intermediate of the form [¹O₂*n(H,D)₂O 3MI] where at least an O-(H,D) bond is weakened. However, the inclusion of these paths in Scheme 2 demands such a large number of kinetically parameters that the fitting procedure becomes practically impossible.

ACKNOWLEDGEMENTS

This work has been supported by a Portuguese financial program PRAXIS/C/SAU/35/96 and a PhD grant 12300/BD. We are grateful to Prof. S. B. Costa for the flash photolysis facilities.

Recebido em 18/7/07; aceito em 17/12/07; publicado na web em 31/7/08

APPENDIX

Bilski and co-workers¹⁰ had already verified that the ¹O₂* lifetime in water/dioxane solvent mixtures (in the absence of an oxidable substrate) is not fittable with the usual sum of the empirical solvent descriptors, such as π, α, β, δH, etc. In fact, there is no need for such solvent descriptors to explain the ¹O₂* lifetime behavior as a function of solvent composition. As already found by Rodgers,⁹ the deactivation of ¹O₂* in solvents or in binary solvent mixtures is due to a bimolecular collision mechanism. For solvent mixtures used in this work, the ¹O₂* deactivation rate is then given by Equation 12.

where X=H or D and m, n are the order of the deactivation relative to each one of the pure solvent and [Y] is the Y solvent molarity.

The parameters obtained fitting Equation 12 to Bilski data by least square method are: m = n = 1 ; k_o = 0.0403 s^-1 ; k_Dx = 3213 M^-1 s^-1 ; = 3980 and = 275 M^-1 s^-1.

These results confirm Rodgers' observation for acetone/benzene and acetone-H₆/acetone-D₆ mixtures concerning the bimolecular character of the singlet oxygen deactivation.^7,9

The same kind of relation can also be found for other aqueous solvent mixtures. For instance, in water or deuterated water/acetonitrile mixtures, the experimental data from Bilski, fitted to Equation A.1, gives: m = n = 1 ; k_o = 7.49 s^-1 ; k_MeCN = 748 M^-1 s^-1; = 3739 and = 280 M^-1 s^-1. The fitted curves are shown in Figures. 6 and 7. The only bad fit is explainable by an isotopic exchange between deuterated water and hydrogenated acetonitrile already reported in the literature.³²

These results demonstrate that a collision mechanism with at least one hydrogen (or deuterium) abstraction is enough to explain the physical ¹O₂* deactivation in binary solutions, in the absence of an oxidable substrate. The rate constants for collision with water (deuterated or not) are independent of the organic pure solvent used in the mixture. The fact that k_H2O >> k_D2O is compatible with a molecular mechanism involving an X (H or D) abstraction or, at least, an O-X bond weakening.²⁷ In literature, an electronic to vibrational energy transfer is claimed to have the same isotopic effect.⁷

• 1. Davies, M. J.; Photochem. Photobiol. Sci. 2004, 3, 17.
• 2. Sá e Melo, T.; Averbeck, D.; Bensasson, R. V.; Land, E. J.; Salet, C.; Photochem. Photobiol 1979, 30, 645.
• 3. Foote, C. S. In Photosensitisation, Molecular, Cellular and Medical Aspects; Moreno, G.; Pottier, R. H.; Truscott, T. G., eds.; Springer-Verlag: Berlin, 1988, vol. H15, p. 125.
• 4. Sá e Melo, T.; Bazin, M.; Ronfard-Haret, J.-C.; Santus, R.; Photochem. Photobiol. 1993, 58, 19.
• 5. Wilkinson, F.; Helman, W. P.; Ross, A. B.; J. Phys. Chem. Ref. Data 1995, 24, 663.
• 6. Zebger, I.; Snyder, J. W.; Andersen, L. K.; Poulsen, L.; Gao, Z.; Lambert, J. D. C.; Kristiansen, U.; Ogilby, P. R.; Photochem. Photobiol. 2004, 79, 319.
• 7. Schweitzer, C.; Schmidt, R.; Chem. Rev. 2003, 103, 1685.
• 8. Cosa, G.; Scaiano, J. C.; Photochem. Photobiol. 2004, 80, 159.
• 9. Rodgers, M. A.; J. Am. Chem. Soc. 1983, 105, 6201.
• 10. Bilski, P.; Holt, R. N.; Chignell, C. F.; J. Photochem. Photobiol., A 1997, 109, 243.
• 11. Michaeli, A.; Feitelson, J.; Photochem. Photobiol. 1994, 59, 284.
• 12. Lemp, E.; Pizarro, N.; Encinas, M. V.; Zanocco, A.; Phys. Chem. Chem. Phys. 2001, 3, 5222.
• 13. Palumbo, M. C.; Garcia, N. A.; Arguello, G. A.; J. Photochem. Photobiol., B 1990, 7, 33.
• 14. Lemp, E.; Zanocco, A. L.; Lissi, E. A.; Curr. Org. Chem. 2003, 7, 799.
• 15. Frimer, A. A.; Spectrum-J. State Gov. 2000, 13, 9.
• 16. Aubry, J. M.; Cazin, B. M.; Rougee, M.; Bensasson, R. V.; J. Am. Chem. Soc. 1995, 117, 9159.
• 17. Carreno, M. C.; Gonzalez-Lopez, M.; Urbano, A.; Angew. Chem., Int. Ed. 2006, 45, 2737.
• 18. Murov, S. L.; Carmichael, I.; Hug, G. L.; Handbook of Photochemistry, Marcel Dekker, Inc.: New York; 2^nd ed., 1993, p. 300.
• 19. Steinhoff, B. A.; Stahl, S. S.; J. Am. Chem. Soc. 2006, 128, 4348.
• 20. Bensasson, R. V.; Land, E. J.; Salet, C.; Photochem. Photobiol. 1978, 27, 273.
• 21. Bensasson, R. V.; Chalvet, O.; Land, E. J.; Ronfard-Haret, J. C.; Photochem. Photobiol. 1984, 39, 287.
• 22. Schwartz, B. J.; Rossky, P. J.; J. Chem. Phys. 1996, 105, 6997.
• 23. Sá e Melo, T.; Maçanita, A.; Prieto, M.; Bazin, M.; Ronfard-Haret, J.-C.; Santus, R.; Photochem. Photobiol. 1988, 48, 429.
• 24. Kamlet, M. J.; Abboud, J. L. M.; Abraham, M. H.; Taft, R. W.; J. Org. Chem. 1983, 48, 2877.
• 25. Casassas, E.; Fonrodona, G.; de Juan, A.; Anales de Quimica 1991, 87, 611.
• 26. Wentworth, P. Jr.; Jones, L. H.; Wentworth, A. D.;. Zhu, X; Larsen, N. A.; Wilson, I. A.; Xu, X.; Goddard III, W. A.; Janda, K. D.; Eschenmoser, A.; Lerner, R. A.; Science 2001, 293, 1806.
• 27. Pilling, M. J.; Seakins, P. W.; Reaction Kinetics, Oxford University Press: New York, 1995, p. 80.
• 28. Bardez, E.; Fedorov, A.; Berberan-Santos, M. N.; Martinho, J. M. G.; J. Phys. Chem. A 1999, 103, 4131.
• 29. Engdahl, A.; Nelander, B.; Science 2002, 295, 482.
• 30. Xu, X.; Muller, R. P.; Goddard III, W. A.; Proc. Nat. Acad. Sci. U. S. A. 2002, 99, 3376.
• 31. Lemp, E.; Zanocco, A. L.; Günther, G.; J. Photochem. Photobiol., B 2001, 65, 165.
• 32. Heck, G.; Mileham, C.; Martin, G. J.; Analusis 1997, 25, 202.

Publication Dates

• Publication in this collection
  10 Oct 2008
• Date of issue
  2008

History

• Accepted
  17 Dec 2007
• Received
  18 July 2007