The "running in the rain" problem revisited: an analytical and numerical approach

O problema "correndo na chuva" revisitado: uma abordagem analítica e numérica

ARTIGOS GERAIS

The "running in the rain" problem revisited: an analytical and numerical approach

O problema "correndo na chuva" revisitado: uma abordagem analítica e numérica

T. Kroetz¹

Departamento de Física, Instituto Tecnológico de Aeronáutica, Centro Técnico Aeroespacial, São José dos Campos, SP, Brazil

ABSTRACT

The dependence between the speed of an object that travels a given distance through the rain and the volume of water dumped on it by the raindrops is examined in this work. Considering a model based on the average distance between the raindrops, it is possible to obtain an analytical equation that expresses this dependence in terms of physical rain parameters. In order to verify our results a more realistic and sophisticated model considering the random nature of the raindrops distribution in the space was built.

Keywords: running in the rain, raindrops distribution.

RESUMO

A dependência entre a velocidade com a qual um objeto percorre uma determinada distância na chuva e o volume de água despejado nele pelas gotas é examinada neste trabalho. Considerando um modelo baseado na distância média entre as gotas é possível obter uma equação analítica que expressa esta dependência em termos dos parâmetros físicos da chuva. A fim de verificar nossos resultados construímos um modelo mais realista e sofisticado que considera a natureza randômica da distribuição de gotas de chuva no espaço.

Palavras-chave: correndo na chuva, distribuição de gotas de chuva.

1. Introduction

The theoretical physics methodology is based on the construction of models that represent the real system which is intended to be studied. The models preserve the essential features and discard the less important details to the systems description through the suitable choices of assumptions and simplifications. Analyzing a model is possible to obtain comparable results with experimental measures of the real system and so the model can be considered plausible or refuted. In the present work this methodology is didactically exemplified through a curious question: What is the best speed to cross a certain distance under rain (without an umbrella) in order to arrive as dry as possible?

This problem was investigated in previous works. In [1] was obtained an analytical expression, derived from a flux argument, which gives the number of raindrops hitting one inclined plane crossing the rain in terms of its horizontal velocity. Another equivalent expression is developed in [2] for a rectangular parallelepiped run ning in the rain considering the apparent inclined direction of the raindrops trajectory due to the speed of the object. The last work mentioned applied the idea of average distances of the raindrops. This concept is also used in our approach but in a different way. Both works do not consider the lateral velocity of drops. In [3] the author investigates the problem with a model considering a "volume of rain per unit volume of air" including the lateral incidence of drops. The conclusions of these works are the same: if the object travels faster it will arrive drier, excepting when the horizontal velocity of the rain is in the same direction as the motion of the object. They also agreed that there is a limit of raindrops collected by the object when its velocity goes to infinity, indicating that there are no great advantages on running at very fast speeds instead of at a standard speed. However, they are unclear on how the parameters of the models are related to the real rain ones (like precipitation rate and volume of the drops), so that the comparison of the results with any experiment becomes very difficult to be done (or maybe impossible).

A new model was built in this work, describing the rain as a three-dimensional lattice, moving towards each direction at velocity components of the raindrops. An analytical expression in terms of physical rain parameters is obtained through the model. The expression gives water volume dumped on one object as function of velocity at which it travels a certain distance under the rain. This expression is completely comparable with experimental results because all the terms presented in the final theoretical relation are measurable. In addition to it, a more complex model that makes use of a computational algorithm was created in order to confront the results extracted from the analytical expression. As the work only requires basic principles of physics and math and includes a detailed mathematic development of the final relation, the paper becomes interesting to the physics education. It provides an elucidative example of the theoretical physics methodology to the undergraduate students in the first years of physics graduation course.

2. The Lattice Rain Model (LRM)

In order to obtain an expression that gives the water volume dumped on one object at the end of its travel under the rain, we constructed a model problem called "Lattice Rain Model" (LRM). In this model, the rain consists of a three-dimensional lattice with tetragonal unit cell where each lattice element corresponds to one raindrop. There are two characteristic cell edges: one horizontal a and one vertical b. Each lattice element moves in (, , ) coordinates at the velocity components of the rain respectively. This construction was based in the assumption that, for a homogenous rain, the distance between one raindrop and its neighbor along one coordinate axis is very similar to the average distance between each drop and its respective neighbors in this same axis. Considering an isotropic rain along and directions, the cell edges must be equal in these directions. The velocities are constant. The vertical direction velocity vrz can be considered constant because drops fall only a few meters before reaching the terminal veloc ity [4].

In order to represent a person running in the rain, a box with horizontal, frontal and lateral areas: A_xy , A_yz and A_xz respectively is taken into consideration. The object moves along the x-direction with velocity v_p for a distance D. A representation of the model problem is shown in Fig. 1. Only a piece of the lattice is represented in the scheme, but is considered that it would fill all the space.

Defining t^'= b/|v_rz| as the time between two consecutive horizontal planes of the lattice reach the ground, we express b as

where t^' has an unknown value for while. In order to relate a and b with the real rain parameters, a measure of rain intensity commonly called "precipitation rate" P is introduced. This parameter is defined in terms of the volume of water V dumped on an arbitrary horizontal area A_h during the time t as

and, in general, it is given in units of mm/h. In our calculations, the MKS system is used, i.e., P will be given in units of m/s. If we use A_xy as the horizontal area and t^' as the time in Eq. (2), it is possible to obtain the water volume contained in just one horizontal plane (see the definition of t^' above) of the lattice with the same area of the top of the body.

On the other hand, the number of drops in one horizontal plane of rain lattice with sides L_x and L_y is given, as we can see in Fig. 2 (a), by

Therefore, if V_d is the volume of each drop, the volume V_xy can also be represented by

The Eqs. (3) and (5) were obtained independently. While the definition of P was used to get the first, the lattice parameter a associated with the rain parameter V_d were used to get the second one. Equaling the right sides of these equations, the length a can be expressed by

The number of drops in one frontal plane of rain lattice with sides L_y and h is given, as we can see in Fig. 2 (b), by

Similarly, the number of drops in one lateral plane of the rain lattice with sides L_x and h is given by

Using Eqs. (1) and (6) in Eqs. (7) and (8) is possible to obtain the expressions

and

Multiplying N_yz and N_xz respectively by the number of frontal and lateral rain planes crossed by the body in its movement, it is possible to obtain the number of raindrops hitting it on each side at the end of the travel. The water volume dumped on the body on A_yz (A_xz) is called V_F (V_L) and it is given by the drop volume V_d multiplied by N_yz (N_xz) and the number of frontal (lateral) planes crossed by the body during the travel

where the number of planes crossed in one direction is written as the travel time t multiplied by relative velocity between the body and the rain along the considered direction and divided by the distance between to consecutive planes. The absolute value of relative velocities were used because the number of raindrops hitting the body can not be negative.

Replacing a, N_yz and N_xz in the Eqs. (11) and (12) by the expressions (6), (9) and (10) respectively, the frontal and lateral volume will be given by

It is interesting to observe that the arbitrary parameter t' was vanished when the number of drops in one plane was multiplied by the number of planes crossed by the body, although we define the lattice characteristic cell edge b in terms of it. The parameter t' was important on the mathematical development, but the final result does not depend on any specific choice of t' value. The volume of water dumped on the top of the body V_T will be given by the expression (2) replacing A_h by A_xy

The total water volume on the body when it finishes its travel will be the sum of expressions (13), (14) and (15).

where t is the travel time. The travel time will be given by the expression D/v_p when the distance D is predetermined. So the Eq. (16) assumes the form

The limits of Eq. (17) are

The above limits indicate that V_total decreases from the infinity (for v_p = 0) to a non-zero value when v_p

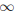. For a negative value of v_rx (the x-velocity of the rain against the motion of the body), the numerator of the middle term in the brackets of Eq. (17) is always greater than unity (since v_p is positive by definition) and tends to one as v_p

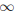. It indicates that there is no minimum in the function V_total(v_p) and it decreases asymptotically to the limit value of Eq. (19). Therefore, the best speed to run for a distance D through the rain which presents horizontal velocity against the runner's motion would be the fastest one that might be possible to reach, in order to Vtotal becomes as close as possible to PD

However, if v_rx is positive (the x-velocity of the rain in the same direction as the motion of the object), then there is an optimal velocity v_p = v_rx that cancels the middle term in the brackets of Eq. (17). It means that if the velocity of the body and the x-velocity of the rain present the same values, then the water volume dumped on frontal (or back) area will be zero. For this value of v_p the total water volume dumped on the body at the end of the travel is given by

It is possible to wonder if it would be better to run as rapidly as possible or at the speed v_p = v_rx in order to arrive drier, in case of a positive value for v_rx. In other words: is it better to cancel the middle term or the first and third terms in Eq. (17)? The first option will be better when the right side of Eq. (20) has a lower value than the right side of Eq. (19). This will occur when

where 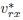is the value of x-velocity of the rain which obeys the relation V_total(v_p = 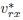) = limv_p

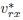V_total. If v_rx < and v_p = v_rx, then the water volume on the area A_yz remains zero, but the body spends too much time crossing the distance D and the water volume dumped on its top and lateral areas makes the option of running at a velocity v_p = v_rx not the best one.

3. The Random Rain Model (RRM)

Could the results obtained with the LRM remain valid for a real rain? A conclusive answer to this question can only be given through a comparison between experimental results and the theoretical ones, extracted from the Eq. (17), but this is not the scope of this work. However, a more sophisticated and totally independent model could be elaborated in order to confront results. It considers the main differences between the lattice model and the real rain: the random position of drops formation and the individual movement of each drop. This model is called "Random Rain Model"(RRM). The only way to extract results from it is making use of a computational algorithm².

The algorithm considers a rain confined in a rectangular parallelepiped of sides D (distance to be crossed by the body), L_y (width of the object) and h (height of the object). Each drop is formed on the top of the parallelepiped, after the time interval dt since the previous drop was created. The initial horizontal position of the drops is chosen randomly, i.e., (x₀,y₀,z₀)= (rand x D, rand x L_y,h), where rand is a random number into the interval (0, 1). The i-th drop moves according the cinematic equations: (x⁽ⁱ⁾,y⁽ⁱ⁾,z⁽ⁱ⁾= where t⁽ⁱ⁾ is the time passed since when the i-th drop was formed. The velocities (v_rx,v_ry,v_rz) are the same for all drops.

The boundary conditions of the space is cyclic on laterals. This means that when a drop crosses one side of the parallelepiped, leaving the space, it reappears on the opposite side preserving the other two coordinates. Every time a drop reaches the floor it is eliminated by the algorithm and another drop is created on the top of space at a new random initial position (x₀,y₀). So, the number of drops into the parallelepiped is always the same. The parallelepiped space represents a piece of a rain as a whole. The justification of the RRM cyclic lateral boundary condition is due to the assumption that the piece of rain considered repeats almost identically along x-direction and y-direction for a homogeneous real rain. In other words, the RRM only permits only new drop information entering into the space from the top area.

While the drops are moving in the space as described above, a rectangular object of dimension L_x, L_y and h moves in x-direction through the distance D at velocity v_p. The algorithm counts every drop hitting the lateral, frontal and back area of the body during its travel. Because the space has the same height of the object, a drop hitting the top area of the body is counted when the initial horizontal position of the drop is contained on the top area of the object at the time of drop creation. At the end of the travel along D, the water volume dumped on the body is obtained multiplying the total number of hitting drops counted by the volume of the drop V_d chosen. A representation of the RRM is shown in Fig. 3.

The drop formation time interval dt and the volume of the drop V_d are directly related to the precipitation rate P. For the RRM, it is known that if the time of rain exposure is dt, then the water volume dumped is the volume of just one drop V_d. So, for the RRM, the precipitation rate will be given by

where DL_y is the area of the floor which receives the rain incidence. In order to relate the numerical parameter dt with the real rain parameters P and V_d, dt was placed on the left side of Eq. (22)

4. Results

The water volume dumped on the object for several values of v_p were obtained from LRM and RRM and the two functions were plotted in the same graph. The same value of parameters in both models were used in order to compare the results. The precipitation rate will be taken as P = 4 mm/h = 1.11 x 10^-6 m/s (a moderate rain). The body dimensions assume values close to human body dimensions: L_x = 0.2m, L_y = 0.4 m and h = 1.8 m. Consequently, the areas in Eq. (17) will be A_xy = L_x x L_y = 0.08 m² , A_yz = Ly x h = 0.72 m² and A_xz = L_x x h = 0.36 m² . The travel distance and the lateral rain velocity will be chosen as D = 100 m and v_ry = 3 m/s. The terminal velocity v_rz depends on the size of the drops. For a drop with radius r = 1.375 mm (V_d =1.089 x 10^-8 m³) the terminal velocity is about v_rz = -7.75 m/s [4]. The time interval of drop formation in the RRM must be dt =2.45 x 10^-4 when the above values for V_d, P, D and L_y are inserted in the Eq. (23).

When the v_rx is negative (positive), the drops hits the frontal (back) area of the body. Moreover, positive and negative values of v_rx must be analyzed separately in order to explore this two different situations.

4.1. The x-velocity of the rain against the motion of the body

If we choose the value v_rx = -3 m/s for x-direction velocity, the dependence between V_total and v_p, for each model, is shown on Fig. 4. The absence of minimum in the graph allows to conclude that the object should travel the distance D as fast as possible in order to arrive drier. However, as the relation between V_total and v_p is not linear, the gain running at very fast speed could not be very significant in comparison to running at moderate speed. For example: travelling at 5 m/s (a normal run) the object arrives 68% less wet than if it travels at 1 m/s (a slow walk). But if it runs at 10 m/s (close to world record speed) it will arrive just 74% less wet than at 1 m/s. The gain difference is only 6% while the run is 100% faster than 5 m/s.

It is possible to observe that the results obtained from LRM and RRM show great similarities. As the RRM is a model based on random variables, consequently its results will be different each time we run the algorithm. However, the difference will just be a statistical fluctuation, and the general behavior will be always the same. The LRM is a model based on the average distances of the raindrops horizontally and vertically. Since LRM ignores the statistical fluctuation on the distances, the red curve in Fig. 4 is smooth and just represents the general behavior of the RRM results.

4.2. The x-velocity of the rain on the same direction of motion of the body

In section 2., it was predicted that there is an optimal velocity that cancels the drops incidence on the frontal (or back) area A_xz for a positive v_rx. But, when the value of v_rx is small, it could not worth to run at this velocity because the body would be exposed to the rain for an extremely long time. The Eq. (21) gives the lower limit of v_rx which makes V_total a minimum for v_p = v_rx. Substituting the values of v_ry, v_rz, A_yz, A_xy and A_xz used in simulations in Eq. (21), we find that this limit must be 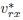= 2.361 m/s.

In order to test the expression (21), we plot two dependencies between V and v_p with positive v_rx. The plot shown on Fig. 5 is for v_rx = 2 m/s (a lower value than 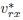). The plot shown in Fig. 6 is for v_rx = 3 m/s (a higher value than 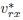). The similarity between LRM and RRM is verified again. In adition to it, we can check that when v_rx > 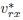, the object arrives drier when running at the speed v_p = v_rx. In case of v_rx < 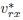, the ideal v_p is the fastest as possible (as seen in the case of negative v_rx).

5. Conclusions

Two models have been proposed that enable the study the "running in the rain"problem. The LRM considers a rain with drops in sites of a three-dimensional lattice. An analytical expression which gives the relation between the speed of a running body under the rain and the water volume on it at the end of its travel was obtained through this model. The second model is the RRM, a numerical model which considers each drop individually (and not on equidistant planes, as considered by LRM) and being formed on random initial positions. Although the RRM reproduces more authentically the main features of the real rain, the results obtained by RRM and LRM are almost identical. The difference resides in small statistical fluctuations on RRM results which will be distinct each time we run the algorithm (since it uses random variables). The details included in the RRM do not contribute significantly to a refined result. It also can not provide an analytic relation as the LRM. So, the main role of RRM was to give credibility to Eq. (17). The main goal of this work is to obtain the oretical results that can be comparable to experimental results, since all parameters present in Eq. (17) can be known experimentally. It is also a simple and didactic example on how the theoretical physics methodology works.

The results from this work indicate that when the rain falls perpendicularly to the top area of the body, or hitting it on its frontal area, the best speed to cross the rain is as fast as possible. Although running being better than walking, the advantages of running faster than a conventional speed run could not worth the ad ditional effort, as it was already observed in [2]. In case of the rain hitting the body on its back area, it could be better to run at the velocity component of the rain parallel to the motion of the body. Considering the Eq. (21) it is possible to decide if running at this spe cific speed is the best option or not. This calculation is a bit unpractical on the daily life as a requisite to take a decision. There are alternative solutions which are more convenient to be applied. For exemple: the person who needs to run in the rain could just observe the inclination of drops trajectory in relation of his back area and intuitively assess if the lower limit of Eq. (21) is respected or not. Even when v_rz < 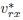, the water volume decreases drastically for v_p = v_rz and passes to decrease slowly for v_p > v_rz , as we can see in Fig. 5. Consequently, there is no great advantages on running at a speed much faster than v_p = v_rz.

The theoretical results obtained from the models are no longer applicable in everyday life when the distance D is extremely extensive. There is a limit on how wet a person could get, because after that the body is considered soaked and even if more drops hit it, the body can not get wetter. When the distance D is very long, this limit can be achieved. So, a person who needs to cross a long distance in the rain would walk quietly for not getting tired (unless he/she feels cold).

6. Acknowledgments

The author would like to thank Alexandre M. Zabot for the encouragement, revision and helpful discussions.

Recebido em 31/3/2009

Revisado em 23/6/2009

Aceito em 7/7/2009

Publicado em 18/2/2010

• [1] S.A. Stern, American Journal of Physics 51, 815 (1983).
• [2] A. De Angelis, European Journal of Physics 8, 201 (1987).
• [3] H. Bailey, The College Mathematics Journal 33, 88 (2002).
• [4] P.K. Wang and H.R. Pruppacher, Journal of Applied Meteorology 16, 275 (1977).

2

The algorithm is written in Fortran language and the author could provide it by e-mail.

Publication Dates

• Publication in this collection
  26 Apr 2010
• Date of issue
  Dec 2009

History

• Accepted
  18 Feb 2010
• Reviewed
  23 June 2009
• Received
  31 Mar 2009