Flexural behavior analysis of a composite of high-strength wire mesh and polyurethane cement (HSWM-PUC)

ABSTRACT

In this paper, a total of 12 groups of thin plate-shaped specimens were designed and produced to investigate the flexural behavior of HSSWM-PUC composite materials through four-point bending tests, considering the effects of parameters such as rubber-powder ratio, reinforcement ratio and specimen width on the flexural behavior of the materials. Based on the test study, flexural load capacity calculations and finite element parametric analysis of HSSWM-PUC composite materials were carried out. As the reinforcement ratio of HSSWM increased, the ultimate load of the specimen increased accordingly. The ultimate load of the specimen with the highest reinforcement ratio was 8.99 kN, which was 63% higher than that of the specimen with the lowest reinforcement ratio. Increased width of thin plate-shaped specimens can improve the flexural load carrying capacity of HSSWM-PUC composite materials while increasing the flexural stiffness of the composite materials. When the width of the specimen increased from 70 mm to 130 mm, the ultimate load increased by 115%, and the maximum deflection decreased by 55%. Based on the simplified intrinsic relationship model of the materials, the flexural load capacity calculation formula of thin plate-shaped specimens of HSSWM-PUC composite materials was proposed. Through finite element analysis, the change rule of the bending performance of the thin plate was investigated, and the test results were effectively verified. Meanwhile, this paper proposed the optimisation direction of PUC mixing ratios to support the design and project implementation of HSSWM-PUC composite materials in the future.

Keywords:
HSSWM-PUC composite materials; Four-point bending test; Ontological relationship; Finite element simulation

1. INTRODUCTION

With the rapid growth of China’s traffic and transportation volume, vehicle transport load is increasing, coupled with the erosion of rain, snow, weathering and other natural conditions, a large number of bridges constructed earlier appear one after another diseases [¹,²,³]. If the damaged bridge is demolished and rebuilt, it will result both in disruption to the normal flow of the road and in huge economic losses [⁴, ⁵]. Therefore, repair and reinforcement of bridges have greater economic significance and social benefits, in line with China’s long-term green and sustainable development strategy.

Strand wire mesh itself has good tensile strength and durability, and can increase the stiffness and bearing capacity of the reinforced beams, often used in bridge reinforcement [⁶,⁷,⁸]. Strand wire mesh is often used as a bonding and anchoring material for concrete with a cementitious base such as polymer mortar or engineered cementitious composite (ECC) [⁹,¹⁰,¹¹,¹²,¹³,¹⁴]. It can adapt well to uneven concrete surfaces. LIAO et al. [¹⁵] conducted an experimental study on reinforced concrete T-beams strengthened by strand wire mesh-polymer mortar composite materials through one control beam and four reinforcement beams. The test results show that the reinforcement of reinforced concrete T-beams with strand mesh-polymer mortar composites can effectively improve the stiffness of the reinforced beams, and the stiffness of all the reinforced beams is larger than that of the control beams. However, the tensile strength and bonding properties of polymer mortar materials have certain limitations [¹⁶, ¹⁷], which can easily lead to cracking of the strand wire mesh-polymer mortar reinforcement layer and peeling of the reinforcement layer from the concrete surface. ZOU et al. [¹⁸] conducted a study on the flexural performance of reinforced concrete beams strengthened with strand wire mesh-ECC. The test results show that reinforced concrete beams reinforced with strand wire mesh-ECC can improve the beam’s bending strength, ductility, stiffness and toughness, and can delay the development of cracks. However, the ECC materials has poor bonding with the reinforced beams and it is easy to peel off the strand mesh-ECC reinforcement layer from the reinforced beams [¹⁹,²⁰,²¹].

PUC composite materials are gradually applied in the field of bridge reinforcement [²²,²³,²⁴]. PUC composite materials are a new type of composite materials with polyurethane as the matrix and cement as the reinforcement, which has the advantages of corrosion resistance, light weight, high strength and so on. ZHANG et al. [²⁵] conducted a study on the flexural behavior of the steel-reinforced concrete T-beam reinforced with high-strength strand mesh-polyurethane cement composite materials. The test results show that HSSWM-PUC composite materials can significantly improve the flexural load capacity of reinforced beams. Compared with the composite mortar-reinforced beams, the HSSWM-PUC composite materials reinforced beams did not suffer from peeling damage and could inhibit the generation and development of cracks.

In order to further apply HSSWM-PUC composite materials to practical engineering, it is necessary to conduct an in-depth study on the composite materials. In this paper, the damage modes and damage characteristics of thin plate-shaped specimens under loading were investigated by 12 groups of four-point bending tests on thin plate-shaped specimens of HSSWM-PUC composite materials. Determine the maximum deflection of thin plate-shaped specimens by analyzing the load-displacement curves of the specimens. Propose the optimization direction of the PUC ratio to provide a basis for the reinforcement of old bridges with HSSWM-PUC composite materials.

2. TEST OVERVIEW

2.1 Test raw materials

The PUC is made by the polymerizing polyol, polyisocyanate mud, ordinary silicate cement and molecular sieve activated powder. By analyzing the effect of different additives on the basic mechanical properties and fluidity of PUC. Three test mixing ratios with low cost, excellent workability and strength meeting the requirements were obtained through orthogonal tests as shown in Table 1.

Table 1
PUC mixing ratio.

TYPE OF MIXING RATIO	RUBBER-POWDER RATIO	MATERIALS COMPOSITION/%
		ISOCYANATE	POLYESTER POLYOL	MOLECULAR SIEVE ACTIVATION POWDER	FLUIDS	CEMENT
Mixing ratio 1	1.33	28.5	28.2	8.6	0.3	34.4
Mixing ratio 2	1.0	25.0	24.8	10.0	0.2	40.0
Mixing ratio 3	0.75	21.4	21.2	11.4	0.2	45.8

HSSWM consists of single strand wire connected by snaps with diameters of 2.0 mm, 2.4 mm, 3.2 mm and 4.5 mm. As shown in Figure 1, stainless steel strand is made of multiple steel wire strands with a galvanized surface and its tensile strength is 1650 MPa.

Figure 1
High strength strand wire.

2.2 Specimen design

The thin plate-shaped specimens had a length of 400 mm and a thickness of 25 mm. 3 longitudinal strands and 4 transverse strands were arranged at equal intervals inside the specimens to form a strand network. Cross buckles were used to secure the intersection of the transverse and longitudinal strands and anchored on both sides of the formwork. Transverse strand spacing was 100 mm and longitudinal strand spacing ld changed with the width of the specimen. The specific dimensions of the thin plate-shaped specimens are shown in Figure 2.

Figure 2
Dimensions of test specimens (unit: mm).

This section should describe all the materials, procedures and methods used at the experimental or theoretical part of the work.

Three groups of 12 thin plate-shaped specimens were designed and fabricated (3 specimens were fabricated for each specimen). The thickness parameters of the specimens were 130 mm, 110 mm, 90 mm and 70 mm, and the parameters of the PUC rubber-powder ratio were 0.75, 1.00 and 1.33. Detailed design parameters are shown in Table 2. Group A and Group C considered the effect of different PUC mixing ratio parameters on flexural behavior. Group B considered the effect of different strand diameter parameters on flexural behavior. Group C considered the effect of different specimen width parameters on flexural behavior.

Table 2
Parameters of thin plate-shaped specimens.

GROUP NUMBER	NUMBER	SPECIMEN WIDTH B/mm	LONGITUDINAL STRAND SPACING LD/mm	STRAND WIRE DIAMETER d/mm	PUC MIXING RATIO
A	A1	130	50	4.5	Mixing ratio 2
	A2	110	40	4.5	Mixing ratio 2
	A3	90	30	4.5	Mixing ratio 2
	A4	70	20	4.5	Mixing ratio 2
B	B1	130	50	4.5	Mixing ratio 3
	B2	130	50	3.2	Mixing ratio 3
	B3	130	50	2.4	Mixing ratio 3
	B4	130	50	2.0	Mixing ratio 3
C	C1	130	50	4.5	Mixing ratio 1
	C2	110	40	4.5	Mixing ratio 1
	C3	90	30	4.5	Mixing ratio 1
	C4	70	20	4.5	Mixing ratio 1

2.3 Specimens production

Test specimen production processes are shown in Figure 3.

Figure 3
Specimen production: (a) fabrication and assembly of wooden formwork, (b) stranding of steel wire, (c) fixing of strands to form strand wire mesh, (d) brushing of release agent, (e) pouring of PUC, (f) demoulding for health.

• (1)

  Made wooden formwork with small holes pre-drilled in the boards for passing through the stranded wire. It is shown in Figure 3(a).

• (2)

  The formwork was formed by passing vertical and horizontal strands through small holes reserved in the formwork, forming a strand network and anchoring the strand ends to the side of the formwork using locking clips, as shown in Figure 3(b).

• (3)

  Secure the strand wire mesh using cross buckles and apply anti-seepage adhesive to the openings where the strand wire passes through the formwork to prevent cement from flowing out. Trim the excess strand wire with strand pliers as shown in Figure 3(c).

• (4)

  Prepare mold release agent with silica gel and talcum powder. Brush the release agent on the inner wall of the formwork to facilitate later mold removal, as shown in Figure 3(d).

• (5)

  Take appropriate amount of polyisocyanate and polyol and pour them into a beaker and put them into a 150° oven to dry for 30 minutes. Prepare the PUC according to the proportion and mix thoroughly, pour the PUC. As shown in Figure 3(e).

• (6)

  After the specimens were poured, the exposed cement surface was covered with cling film, the formwork was removed after 24 h, and the specimens were placed in a standard curing room for curing. After the end of the curing, the specimens were taken out from the standard curing room at a temperature of 20 ± 2°C to prepare for the test, as shown in Figure 3(f).

2.4 Test procedure and damage phenomena

Test equipment is shown in Figure 4. Support and loading head were installed on the testing machine, three displacement gauges were arranged longitudinally at the span center of the thin plate-shaped specimens and under the loading head to determine the vertical deformation of the specimens. Thin plate-shaped specimens were placed on a support and the upper and lower surfaces of the specimens were cleaned with alcohol. Strain gauges were applied to the upper and lower surfaces to determine the compressive strain. The loading of the test was displacement controlled with a constant loading rate of 0.5 mm/min.

Figure 4
Test equipment schematic diagram.

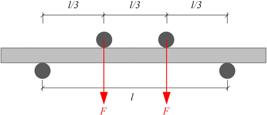
Flexural tests are categorized into three-point bending and four-point bending according to the number of loading points. Four-point bending test destructive load is smaller than the three-point bending test destructive load, the rigidity of the test machine is less demanding, and the reliability is relatively high. This test used four points of 1/3 bending. Two supports were 300 mm apart, the distance between the loading point and the support was 100 mm, and the distance between the two loading points was 100 mm. The loading position is shown in Figure 5.

Figure 5
Load position.

After the test started, universal testing machine pulled the loading head to move downward. When the loading head came into contact with the thin plate-shaped specimens, the load value and displacement value increased uniformly. With the continuously increased load, the thin plate-shaped specimens gradually deformed, accompanied by a crisp fracture sound, a long crack appeared in the middle of the specimens, and the PUC was damaged. As shown in Figure 6. In the event of damage, the fracture of the strand occurred almost simultaneously with the fragmentation of the urethane cement. At this time the thin plate-shaped specimens also reached the ultimate load and maximum deflection.

Figure 6
Damage phenomena.

3. TEST RESULTS

3.1 Group A test results

Groups A and C considered the effect of different PUC mixing ratio parameters on flexural behavior. The ultimate loads and mid-span displacements of Group A specimens were reduced compared to those of Group C. Load-mid-span displacement curves of Group A are shown in Figure 7. Each specimen in group A had smaller ultimate loads, among them, specimen A1 with the largest width possessed the largest growth rate, with an average ultimate load of 10.93 kN, improving by 44% compared with the mean ultimate loading of specimen A4. This indicated that the width increased the load carrying capacity of the specimens more significantly.

Figure 7
Load-mid-span displacement curve of group A.

3.2 Group B test results

Group B considered the effect of different strand diameter parameters on flexural behavior. load-mid-span displacement curves for Group B are shown in Figure 8. With the increased reinforcement ratio, the ultimate load of the specimen increased accordingly, which indicated that the reinforcement ratio was the main factor affecting the flexural behavior of the specimen. Mid-span displacement was also positively correlated with the reinforcement ratio, indicating that the reinforcement ratio not only improved the load carrying capacity of the specimen, but also improved the deformation capacity of the specimen.

Figure 8
Load-mid-span displacement curves for group B.

3.3 Group C test results

Group C considered the effect of different specimen width parameters on flexural behavior. load-mid-span displacement curves for Group C are shown in Figure 9. Specimen C1 had the largest width and possessed the largest average ultimate load. Specimen C4 had the smallest width and possessed the smallest average ultimate load. With the increase in load, the growth rate of mid-span displacement of specimen C1 was significantly smaller than that of specimens C2, C3 and C4. This indicated that higher specimen widths could significantly inhibit the expansion of mid-span displacements, but had essentially no effect on the growth of displacements.

Figure 9
Load-mid-span displacement curve for group C.

4. ANALYSIS OF INFLUENCING FACTORS

4.1 Influence of rubber-powder ratio on flexural behavior

Test results showed that the rubber-powder ratio significantly affects the ultimate load of thin plate-shaped specimens of HSSWM-PUC composite materials. Influence of rubber-powder ratio on flexural behavior is shown in Figure 10. The PUC rubber-powder ratios of specimens A1, B1 and C1 were different. It is shown in Figure 10(a). The rubber-powder ratio had a small effect on the maximum deflection of the specimens, which did not change significantly with the change of the PUC rubber-powder ratio. It is shown in Figure 10(b). Rubber-powder ratio significantly affects the flexural load, where specimen C1 with the largest rubber-powder ratio was subjected to an ultimate load of 13.24 kN, and specimen B1 with the smallest rubber-powder ratio was subjected to an ultimate load of 8.99 kN, which increased the ultimate load by 47%.

Figure 10
Influence of rubber-powder ratio on flexural behavior.

4.2 Influence of reinforcement ratio on flexural behavior

Test results showed that the reinforcement ratio significantly affected the maximum deflection and ultimate load of thin plate-shaped specimens of HSSWM-PUC composite materials. The influence of the reinforcement ratio on the bending test is shown in Figure 11. Group B considered the influence of different reinforcement ratios on the flexural behavior of thin plate-shaped specimens of HSSWM-PUC composite materials. As shown in Figure 11(a). The maximum deflection of the specimen decreased gradually with the increase of reinforcement ratio, which indicated that the reinforcement ratio could improve the flexural stiffness of the specimen and thus reduce the deformation of the specimen under load. As shown in Figure 11(b). The reinforcement ratio was positively correlated with the ultimate load, in which the ultimate load of specimen B1 with the largest reinforcement ratio was 8.99 kN, which was about 63% higher than that of specimen B4 with the smallest reinforcement ratio, indicating that the increase of reinforcement ratio could greatly improve the load carrying capacity of specimens.

Figure 11
Influence of reinforcement ratio on flexural behavior.

4.3 Influence of specimen width on flexural behavior

Group C considered the influence of different specimen widths on the flexural behavior of thin plate-shaped specimens of HSSWM-PUC composite materials. Specimen width influence on flexural behavior is shown in Figure 12. As shown in Figure 12(a). The maximum deflection of the specimen decreased with the increase in width, and the average maximum deflection of specimen C1 was 10.07 mm, which was 1/20 of the average maximum deflection span. As shown in Figure 12(b). Specimen C1 with the largest width had an ultimate load of 13.24 kN, which was about 115% higher than that of specimen C4 with the smallest width, indicating that the increase in time width can significantly improve the flexural load capacity of the specimen.

Figure 12
Influence of specimen width on flexural behavior.

5. THEORETICAL ANALYSIS

5.1 Four-point bending test ontological relationship modeling

5.1.1. Calculation formula for flexural capacity

According to the Chinese national standard “Standard Test Methods for Mechanical Properties of Ordinary Concrete” (GB/T50081-2002) [²⁶], the formula for calculating the flexural strength of ordinary concrete:

Specimen bending, the maximum positive pressure on the surface of the PUC on the tensile side:

(1) $${\sigma }_b=\frac{M_b}{W}$$

Where: σ_b is the concrete flexural strength; Mb is the maximum bending moment;

Flexural section coefficient for thin plate-shaped specimens:

(2) $$W=\frac{b{h}^2}{6}$$

The formula for calculating the flexural strength of thin plate-shaped specimens:

(3) $$f_{\max }=\frac{Fl}{b{h}^2}$$

(4) $$TI=\frac{{\int }_0^{{\delta }_{\max }}F(\delta )d\delta }{bhs}$$

Where: W is the bending section coefficient; b is the width of thin plate-shaped specimens; h is the height of thin plate-shaped specimens; f_max is the ultimate bending strength of thin plate-shaped specimens; δ_max is the ultimate spanwise deflection of thin plate-shaped specimens; F is the specimen destructive load; l is the span between supports; TI is the energy absorption capacity.

5.1.2. Basic assumptions for calculation of flexural capacity

• (1)

  Assumption of plane section: After the polyurethane concrete composite is stressed, the average stresses of the PUC and the longitudinal high-strength strand are linearly distributed along the range of the height of the positive section.

• (2)

  Deformation coordination between high-strength steel strand and PUC composite materials: During the entire bending process, the relative slip between the steel strand and the PUC is not considered.

5.1.3. Flexural load capacity calculation models

• (1)

  Tension modeling of high-strength strand

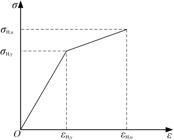
Figure 13 shows the simplified stress-strain relationship model of high strength strand. Its expression is shown in equation (5):

Figure 13
Simplified stress-strain relationship for high-strength strand wire in tension.

(5) $${\sigma }_H=\{\begin{array}{cc}{E}_1{\epsilon }_H& (0\le {\epsilon }_H\le {\epsilon }_{H,y})\\ {\sigma }_{H,y}+E_2({\epsilon }_H-{\epsilon }_{H,y})& ({\epsilon }_{H,y}\le {\epsilon }_H\le {\epsilon }_{H,u})\end{array}$$

Where: E₁ and E₂ are the modulus of elasticity of the strand in the first and second stages, respectively. σ_H,u is the ultimate tensile stress of the strand. σ_H,y is the tensile stress at the end of the first stage of the strand tensioning process, which is about 80% of the ultimate tensile stress σ_H,u of the strand. ε_H,u is the ultimate tensile strain of the strand. ε_H,y is the tensile strain at the end of the first stage of the strand tensioning process, which is about 45% of the ultimate tensile strain. ε_H,u of the strand. Depending on the diameter of the strand, the modulus of elasticity takes different values, as shown in Table 3.

Table 3
Modulus of elasticity values.

DIAMETER (mm)	E1 (MPa)	E2 (MPa)
2.0	135000	32000
2.4	130000	31500
3.2	108000	22500
4.5	97000	21300

• (2)

  PUC compression modeling

Compressive ontological relationship of PUC is shown in Figure 14. From Figure 14(a), it can be seen that the model is divided into rising and smooth segments, which are similar to the compressive stress-strain relationship of ECC. As can be seen from Figure 14(b), the quadratic relationship of the rising section of the model is simplified to a linear relationship for ease of calculation. The simplified expression is shown in equation (6).

Figure 14
PUC stress-strain relationship model under compression.

(6) $${\sigma }_{P,c}=\{\begin{array}{cc}\frac{{\epsilon }_{P,c}}{{\epsilon }_{P,c1}}{\sigma }_{P,c1}& (0\le {\epsilon }_{P,c}\le {\epsilon }_{P,c1})\\ {\sigma }_{P,cu}& ({\epsilon }_{P,c1}\le {\epsilon }_{P,cu})\end{array}$$

Where: σ_P,c represents the PUC pressure strength, ε_P,c1 presents the ultimate pressure strength of the surface of the plate at the time of bending damage of the thin plate specimen. ε_P,cu at the top of the plate is taken as 0.02.

• (3)

  Tension Modeling of PUC

As shown in Figure 15, in this paper, the intrinsic relationship of PUC is simplified from a quadratic relationship to a linear relationship. σ_P,tu and ε_P,tu in the figure are the ultimate tensile stress and ultimate tensile strain of PUC, respectively. The expressions are shown in equation (7).

Figure 15
Pressure ontological relationship of PUC.

(7) $${\sigma }_{P,t}=E_{P,t}{\epsilon }_{P,t}$$

Where: σ_p,t and ε_p,t are the tensile stress and tensile strain of the PUC, respectively; E_p,t is the simplified tensile modulus of elasticity of the PUC, which is taken as 4500 MPa.

• (4)

  Calculation formula for flexural capacity

In the calculation of flexural load capacity, the specimen is considered to have the stress-strain profile as shown in Figure 16 for the case of PUC and HSSWM working together in the tensile zone.

Figure 16
Stress-strain distribution in cross-section.

Where: a_s is the thickness of the strand protection layer; h₀ is the effective height of the section; h is the height of the specimen; b is the width of the specimen; x₀ is the height of the pressurized zone of the PUC; σ_p,t and ε_p,t are the PUC tensile and ultimate tensile stresses, respectively; σ_H,t and ε_H,t are the stresses and strains in the high-strength strand wire; ε_p,c and ε_p,cu are PUC compressive strain and ultimate compressive strain, respectively; ε_p,cu is the compressive ultimate stress of PUC;Ψ is the tensile stress parameter of PUC.

Based on the stress-strain distribution of the cross-section during bending of the composite materials, equation (8) is derived through the equilibrium equations of force and bending moment:

(8) $$\{\begin{array}{c}\alpha \beta {\sigma }_{P,cu}b{x}_0={\sigma }_H{A}_H+\psi {\sigma }_{P,tu}b(h-x_0)\\ M={\sigma }_H{A}_H\left(h-a_s-\frac{1}{2}\beta x_0\right)+\frac{1}{2}\psi {\sigma }_{p,tu}b(h-x_0)[h+(1-\beta )x_0]\end{array}$$

Strain and stress in HSSWM in the ultimate damage state of thin plate-shaped specimens:

(9) $${\epsilon }_H=\frac{h-x_0-a_H}{x_0}{\epsilon }_{P,cu}$$

(10) $${\sigma }_H=E_1\frac{h-x_0-a_H}{x_0}{\epsilon }_{P,cu}$$

Through the theoretical analysis of the results of the bending properties of cementitious materials, it was determined that the value of the tensile stress parameter Ψ of PUC is 1.25. This can be obtained by substituting equation (10) and the value of Ψ into equation (8).

(11) $$\{\begin{array}{c}\alpha \beta {\sigma }_{P,cu}b{x}_0={\sigma }_H{A}_H+1.25{\sigma }_{P,tu}b(h-x_0)\\ M={\sigma }_H{A}_H\left(h-a_s-\frac{1}{2}\beta x_0\right)+\frac{1}{8}{\sigma }_{p,tu}b(h-x_0)[h+(1-\beta )x_0]\end{array}$$

Where: b means sectional width; h means sectional height, for this test, h is taken as 25 mm for thin plate specimens; σ_H is the high-strength strand stress; a_H is the height of the strand, for thin plate-shaped specimens with strands vertically centered, a_H is taken as 12.5 mm. A_H is the cross sectional area of the longitudinal strand, which is valued according to the strand diameter.

5.2 Approximate calculation of energy absorption capacity

Load-deflection curves do not always seek to increase the ultimate load, if the load is high but the deflection is low, this results in a load-deflection curve that does not necessarily have the largest area of the envelope, the energy absorption capacity is low. The area enveloped by the HSSWM-PUC thin plate-shaped specimens approximates a right triangle, as shown in Figure 17. Specimen C3 with a width of 90 mm has only 76% of the ultimate load of specimen C1 with a width of 130 mm, but it possesses a maximum displacement of 15.59 mm, which is 55% larger compared to specimen C1 with a width of 10.07 mm. The area of the specimen C3 envelope is 117% of that of specimen C1.

Figure 17
Approximate calculation of energy absorption capacity.

5.3 Finite element simulation

In this paper, the most typical group A was selected as the simulation object, and four finite element simulation specimens with different width parameters were established to compare with the test data. The finite element model was established through Abaqus, as shown in Figure 18. In the finite element modeling of thin plate-shaped specimens of HSSWM-PUC composite materials, high-tensile strands and PUC were deformed together by default. By embedding the HSSWM into the PUC, the slip between the materials was not considered. At the same time, the loading points and the support pads were bound and connected to the thin plate-shaped specimens. A generalized algorithm was selected for calculation in the analysis step, with symmetrical loading at the two loading points using incremental automatic control.

Figure 18
Finite element model.

5.3.1. Results of simulation analyses

Tensile damage cloud diagrams of the specimen as a whole and the HSSWM are shown in Figure 19. As shown in Figure 19(a), during the bending process of the specimen, the tensile stress gradually increases from the span center to both ends. As shown in Figure 19(b), inside the thin plate-shaped specimens, the longitudinal strand in the center was the first to reach the maximum tensile stress, with the increase of load, another two longitudinal strands also reached the maximum tensile stress, followed by the damage of the specimens.

Figure 19
Stress maps.

Group A load-displacement curves are shown in Figure 20. As shown, the dashed line was the simulation result and the solid line was the test result, which could be seen by comparing the ultimate loads: Percentage difference between measured and simulated values are 11%, 8%, 5% and 15% respectively. This could be seen by comparing the maximum mid-span displacements: Percentage differences between measured and simulated values were 11%, 10%, 7% and 8%. The test curves were in general agreement with the simulated curves.

Figure 20
Comparison between modeled and real results.

5.3.2. Finite element parametric analysis

On the basis of verifying that the finite element model of thin plate-shaped specimens was reasonable, parametric analyses were carried out on other factors affecting the flexural load carrying capacity of composite materials. The influence of transverse strand spacing on the bending reinforcement effect was simulated for constant specimen width and longitudinal strand spacing. The specific parameters are shown in Table 4.

Table 4
Finite element simulation parameters.

GROUP NUMBER	SPECIMEN WIDTH B/mm	TRANSVERSE STRAND SPACING LB/mm	NUMBER OF TRANSVERSE STRANDS	LONGITUDINAL STRAND SPACING LD/mm	NUMBER OF LONGITUDINAL STRANDS
A1	130	100	4	50	3
D1	130	120	3	50	3
D2	130	80	5	50	3
D3	130	60	6	50	3

Results of the finite element simulation parametric analyses performed with transverse strand spacing and number as variables are shown in Figure 21. As the transverse strand spacing decreases, the ultimate load exists slightly increased, but the growth was not large. This indicated that the transverse strand had a small effect on the ultimate load and the flexural capacity of the thin plate-shaped specimens was mainly determined by the longitudinal strand reinforcement ratio.

Figure 21
Parameter analysis results.

6. CONCLUSIONS

To address the problem of insufficient load-bearing capacity of bridges, this paper proposed the HSSWM-PUC composite materials reinforcement method. In order to verify the feasibility of HSSWM-PUC composite materials for bridge reinforcement, four-point bending tests of thin plate-shaped specimens of HSSWM-PUC composite materials were carried out. Based on the test results, finite element simulations and theoretical analyses were carried out, and the following conclusions were drawn:

• (1)

  This rubber-powder ratio significantly affected the ultimate load of thin plate-shaped specimens of HSSWM-PUC composite materials, but had less effect on the maximum deflection. A rubber-powder ratio of 1.33 increased the ultimate load by 21% and 47% over the rubber-powder ratios of 1 and 0.75, respectively.

• (2)

  The reinforcement rate can significantly increase the extreme capacity and strength of the specimens. Maximum ultimate capacity of the specimens with the highest reinforcement rate was 57% more than the minimum reinforcement rate specimen.

• (3)

  Increasing the width of thin plate-shaped specimens could improve the flexural load capacity of HSSWM-PUC composite materials. Maximum load carrying capacity was obtained for thin plate-shaped specimens with a width of 130 mm, and the ultimate load was increased by 115% compared to that of specimens with a width of 70 mm. The maximum deflection was reduced by 55%. At the same time, the increased width of the specimens could significantly inhibit the growth of the mid-span displacement.

• (4)

  Through Abaqus finite element simulation, the stress distribution and damage mode of thin plate-shaped specimens in the bending process were further understood. By comparing the load-displacement curves during the test and the simulation, it was found that the two were more consistent.

• (5)

  Compared with strand wire mesh-polymer mortar composite materials, HSSWM-PUC composite materials had better adhesion. The HSSWM-PUC composite material reinforced beams underwent bending failure instead of peeling failure, allowing the strength of the high-strength strands to be fully utilized. The theoretical calculation formula proposed in the article could be used to predict the flexural bearing capacity of HSSWM-PUC composite materials, providing theoretical guidance for the application of HSSWM-PUC materials in bridge reinforcement engineering.

7. ACKNOWLEDGMENTS

The authors are grateful for the financial support of the Basic scientific research project of colleges and universities of Liaoning Province Education Department (Project No. LJ212410153032) and the Doctoral Start-up Foundation of Liaoning Province (Project No.2021-BS-168).

8. BIBLIOGRAPHY

• ^[1] ZHANG, G. J., LIU, Y. J., LIU, J., et al, “Causes and statistical characteristics of bridge failures: a review”, Journal of Traffic and Transportation Engineering, v. 9, n. 3, pp. 388–406, 2022. doi: http://doi.org/10.1016/j.jtte.2021.12.003.
  » https://doi.org/10.1016/j.jtte.2021.12.003
• ^[2] ZHANG, K. X., QI, T. Y., LI, D. C., et al, “Research on innovative reinforcement of prestressed T-beam bridge”, International Journal of Structural Integrity, v. 12, n. 6, pp. 922–937, Nov. 2021. doi: http://doi.org/10.1108/IJSI-11-2020-0117.
  » https://doi.org/10.1108/IJSI-11-2020-0117
• ^[3] LI, W. W., XUE, Y. G., DU, Y. L., et al, “Common Diseases of road and bridge engineering and application of construction treatment technology”, Frontiers in Management Research, v. 3, n. 2, pp. 78–83, Apr. 2019. doi: http://doi.org/10.22606/fmr.2019.32004.
  » https://doi.org/10.22606/fmr.2019.32004
• ^[4] TIAN, S. Z., JIA, H. X., LIN, Y. Z., “Hybrid simulation of a carbon fibre-reinforced polymer-strengthened continuous reinforced concrete girder bridge”, Advances in Structural Engineering, v. 20, n. 11, pp. 1658–1670, Feb. 2017. doi: http://doi.org/10.1177/1369433217691772.
  » https://doi.org/10.1177/1369433217691772
• ^[5] LI, J., MA, L. J., “Research on quality inspection and reinforcement technology of road bridge”, Academic Journal of Science and Technology, v. 10, n. 2, pp. 51–54, Apr. 2024. doi: http://doi.org/10.54097/np120e98.
  » https://doi.org/10.54097/np120e98
• ^[6] ZHANG, K. X., QI, T. Y., LI, D. C., et al, “Health monitoring-based assessment of reinforcement with prestressed steel strand for cable-stayed bridge”, Structural Durability & Health Monitoring, v. 16, n. 1, pp. 53–80, Mar. 2022. doi: http://doi.org/10.32604/sdhm.2021.016130.
  » https://doi.org/10.32604/sdhm.2021.016130
• ^[7] LI, B. C., LIU, H. B., JIAN, J. S., et al, “Static load test analysis of t-beam bridge shear strengthening by prestressed steel wire rope embedded in Polyurethane Cement (PSWR-PUC)”, Sustainability (Basel), v. 15, n. 13, pp. 10514, Jul. 2023. doi: http://doi.org/10.3390/su151310514.
  » https://doi.org/10.3390/su151310514
• ^[8] PARK, H., JEONG, S. M., LEE, S. C., et al, “Flexural behavior of post-tensioned prestressed concrete girders with high-strength strands”, Engineering Structures, v. 112, n. 1, pp. 90–99, Apr. 2016. doi: http://doi.org/10.1016/j.engstruct.2016.01.004.
  » https://doi.org/10.1016/j.engstruct.2016.01.004
• ^[9] ZHAO, D. P., LI, K., FAN, J. J., et al, “Shear behavior of RC beams strengthened with high-strength steel strand mesh reinforced ECC: Shear capacity, cracking and deformation”, Engineering Structures, v. 298, n. 1, pp. 117081, Jan. 2024. doi: http://doi.org/10.1016/j.engstruct.2023.117081.
  » https://doi.org/10.1016/j.engstruct.2023.117081
• ^[10] WANG, X. L., LI, Y. P., ZHAO, Y. K., et al, “Compressive performance of RC columns strengthened with high-strength stainless steel wire mesh-ECC under small eccentric compression load”, Buildings, v. 12, n. 10, pp. 1628, Oct. 2022. doi: http://doi.org/10.3390/buildings12101628.
  » https://doi.org/10.3390/buildings12101628
• ^[11] LIU, Z. Q., GUO, Z. X., YE, Y., “Flexural behaviour of RC beams strengthened with prestressed steel wire ropes polymer mortar composite”, Journal of Asian Architecture and Building Engineering, v. 21, n. 1, pp. 48–65, May. 2021. doi: http://doi.org/10.1080/13467581.2021.1928508.
  » https://doi.org/10.1080/13467581.2021.1928508
• ^[12] THANGARAJ, R. P., SHANMUGAM, B., “Performance of RC beams developed with ECC layer and AR glass fiber mesh under flexural loading”, Matéria (Rio de Janeiro), v. 29, n. 3, pp. e20240125, Jan. 2024. doi: http://doi.org/10.1590/1517-7076-rmat-2024-0125.
  » https://doi.org/10.1590/1517-7076-rmat-2024-0125
• ^[13] WEI, Y. X., LI, K., FAN, J. J., et al, “Seismic response of RC short columns strengthened by high-strength stainless steel wire rope meshes reinforced ECC jacket”, Construction & Building Materials, v. 439, n. 1, pp. 137419, Aug. 2024. doi: http://doi.org/10.1016/j.conbuildmat.2024.137419.
  » https://doi.org/10.1016/j.conbuildmat.2024.137419
• ^[14] XING, G. H., WU, T., LIU, B. S., et al, “Experimental investigation of reinforced concrete T-beams strengthened with steel wire mesh embedded in polymer mortar overlay”, Advances in Structural Engineering, v. 13, n. 1, pp. 69–79, Nov. 2016. doi: http://doi.org/10.1260/1369-4332.13.1.69.
  » https://doi.org/10.1260/1369-4332.13.1.69
• ^[15] LIAO, W. Z., WANG, H. W., LI, M., et al, “Large scale experimental study on bond behavior between polymer modified cement mortar layer and concrete”, Construction & Building Materials, v. 228, n. 20, pp. 116751, Dec. 2019. doi: http://doi.org/10.1016/j.conbuildmat.2019.116751.
  » https://doi.org/10.1016/j.conbuildmat.2019.116751
• ^[16] ALJAZAERI, Z. R., MYERS, J., “Rehabilitation and strengthening of reinforced concrete members using a fiber reinforced cementitious matrix composite”, Journal of Materials in Civil Engineering, v. 30, n. 7, pp. 04018120, Apr. 2018. doi: http://doi.org/10.1061/(ASCE)MT.1943-5533.0002299.
  » https://doi.org/10.1061/(ASCE)MT.1943-5533.0002299
• ^[17] LI, K., WEI, Y. X., LI, Y. P., et al, “Flexural behavior of reinforced concrete beams strengthened with high-strength stainless steel wire rope meshes reinforced ECC”, Construction & Building Materials, v. 362, n. 2, pp. 129627, Jan. 2023. doi: http://doi.org/10.1016/j.conbuildmat.2022.129627.
  » https://doi.org/10.1016/j.conbuildmat.2022.129627
• ^[18] ZOU, X. Y., LIU, Y. W., ZHU, J. T., et al, “Analytical and numerical modeling of the pullout behavior between high-strength stainless steel wire mesh and ECC”, Materials (Basel), v. 15, n. 16, pp. 5649, Aug. 2022. doi: http://doi.org/10.3390/ma15165649. PMid:36013784.
  » https://doi.org/10.3390/ma15165649
• ^[19] ZHU, J. T., ZHANG, K., WWANG, X. L., et al, “Bond-slip performance between high-strength steel wire rope meshes and engineered cementitious composites”, Journal of Materials in Civil Engineering, v. 34, n. 5, pp. 04022048, Feb. 2022. doi: http://doi.org/10.1061/(ASCE)MT.1943-5533.0004184.
  » https://doi.org/10.1061/(ASCE)MT.1943-5533.0004184
• ^[20] TIAN, J., WU, X. W., TAN, X., et al, “Experimental study and analysis model of flexural synergistic effect of reinforced concrete beams strengthened with ECC”, Construction & Building Materials, v. 352, n. 17, pp. 128987, Oct. 2022. doi: http://doi.org/10.1016/j.conbuildmat.2022.128987.
  » https://doi.org/10.1016/j.conbuildmat.2022.128987
• ^[21] ZHANG, K. X., SUN, Q. S., “Strengthening of a reinforced concrete bridge with polyurethane-cement composite (PUC)”, The Open Civil Engineering Journal, v. 10, n. 1, pp. 768–781, Nov. 2016. doi: http://doi.org/10.2174/1874149501610010768.
  » https://doi.org/10.2174/1874149501610010768
• ^[22] GAO, H. S., DONG, Y. Q., ZHANG, K. X., et al, “Study on mechanical properties of lightweight and high strength polyurethane cement composite (PUC)”, Journal of Physics: Conference Series, v. 1965, n. 1, pp. 012075, Jun. 2021. doi: http://doi.org/10.1088/1742-6596/1965/1/012075.
  » https://doi.org/10.1088/1742-6596/1965/1/012075
• ^[23] HUSSAIN, H. K., ZHANG, L. Z., LIU, G. W., “An experimental study on strengthening reinforced concrete T-beams using new material poly-urethane-cement (PUC)”, Construction & Building Materials, v. 40, pp. 104–117, Mar. 2013. doi: http://doi.org/10.1016/j.conbuildmat.2012.09.088.
  » https://doi.org/10.1016/j.conbuildmat.2012.09.088
• ^[24] HUSSAIN, H. K., LIU, G. W., YONG, Y. W., “Experimental study to investigate mechanical properties of new material polyurethane-cement composite (PUC)”, Construction & Building Materials, v. 50, n. 15, pp. 200–208, Jan. 2014. doi: http://doi.org/10.1016/j.conbuildmat.2013.09.035.
  » https://doi.org/10.1016/j.conbuildmat.2013.09.035
• ^[25] ZHANG, K. X., XUAN, J. Q., SHEN, X. Y., et al, “Investigating the flexural properties of reinforced concrete t-beams strengthened with high-strength steel wire mesh and polyurethane cement”, Journal of Bridge Engineering, v. 29, n. 5, pp. 04024023, Mar. 2024. doi: http://doi.org/10.1061/JBENF2.BEENG-6524.
  » https://doi.org/10.1061/JBENF2.BEENG-6524
• ^[26] MINISTRY OF CONSTRUCTION OF PRC, GB/T50081-2002: Standard Test Methods for Mechanical Properties of Ordinary Concrete, Beijing, G B/ T, 2002.

Publication Dates

• Publication in this collection
  10 Jan 2025
• Date of issue
  2024

History

• Received
  20 July 2024
• Accepted
  09 Sept 2024