Ultimate load of Steel Fiber Reinforced Concrete (SFRC) encased light gauge steel column exposed to elevated temperature using computational model approach

ABSTRACT

This research emphasizes the critical role of fire resistance in building structures, with a particular focus on concrete columns, which are vital for maintaining structural integrity during fires. Concrete Encased Steel (CES) columns, featuring steel sections encased in concrete, provide improved ductility, shear strength, and compressive capacity. While the fire-resistant properties of Concrete Filled Steel Tubular (CFST) columns have been widely studied, CES columns are increasingly recognized for their unique advantages. A key research gap exists in predicting the ultimate load of Steel Fiber Reinforced CES columns under elevated temperatures. This study addresses the gap by developing a computational model using Machine Learning (ML) techniques. Forty CES columns, subjected to various conditions such as different concrete types, temperatures, and encasement were experimentally tested. The data was used to train ML algorithms, including Linear Regression (LR), Extreme Gradient Boosting (XGB), Gradient Boost Regressor (GBR), and Voting Regressor (VR), to predict the ultimate load under high temperatures. The model's performance was assessed using R2, RMSE, MSE, and MAE metrics, with XGB outperforming other models by achieving an R2 value of 0.94, indicating excellent predictive accuracy.

Keywords:
Machine Learning (ML); Artificial Intelligence (AI); Concrete Encased Steel (CES); Steel Fiber Reinforced concrete (SFRC); Ultimate load

1. INTRODUCTION

Buildings face significant challenges from exposure to high temperatures, such as those resulting from fire accidents. It is crucial for structures to have adequate fire resistance to either withstand these conditions or, at a minimum, allow occupants enough time to evacuate before experiencing structural failure. Concrete columns are fundamental components in reinforced concrete buildings, as they support the structure and transfer loads to the foundation. Any damage or failure in these columns could lead to partial or complete collapse of the structure due to a chain reaction. In reality, columns subjected to axial loads rarely experience purely axial stress. This is because factors such as initial imperfections, the application of loads by beams and slabs, and moments from continuous construction introduce bending. Construction professionals are therefore particularly concerned with how buildings perform under fire conditions to minimize risks to people and property while maintaining industry standards.

CES columns are a prominent type of composite structural member, comprising concrete, stirrups, longitudinal reinforcements, and an encased steel section. These columns are increasingly utilized in high-rise and super high-rise buildings due to their superior mechanical properties both at room temperature and under elevated temperatures, including fire conditions [¹, ²]. A key benefit of CES columns is that the surrounding concrete effectively mitigates or prevents local and overall buckling of the steel section [², ³]. Additionally, the steel flanges provide confinement to the inner concrete, thereby enhancing its ductility, shear resistance, and compressive strength. The concrete encasement also offers notable fire resistance, thanks to its low thermal conductivity, which slows down the heating of the steel during a fire.

CES columns are drawing increasing attention from researchers as a primary type of vertical load-bearing member. Although much research has been conducted on the fire resistance of steel and concrete composite columns, a significant portion has focused on Concrete Filled Steel Tubular (CFST) columns [⁴, ⁵]. For example, studied the post-fire residual strengths of steel-reinforced concrete-filled square steel tubular columns using both experimental and computational methods. They found that factors such as fire duration, steel section ratio, and section size greatly influence the residual strength [⁶, ⁷, ⁸]. Similarly, examined 135 steel-reinforced CFST stub columns subjected to high temperatures and found that, with an appropriate steel section ratio, the compression resistance remains relatively stable. These studies underscore the significant enhancement in post-fire compression resistance provided by encased steel sections, which is vital for the performance of CES columns [⁹, ¹⁰, ¹¹].

Notable advancements have been made in understanding the fire resistance of CES columns. Tested fourteen encased steel stanchions under various fire conditions [¹²]. Developed analytical models to predict the behavior of CES columns in fire scenarios, proposing formulas to determine their ultimate strength [⁹]. Experimentally investigated how axial restraint affects the fire resistance of CES columns and discussed the influence of load ratios and cross-sectional dimensions using finite element analysis (FEA) [¹³]. Found that, at low load ratios, the stiffness of surrounding structures significantly impacts columns subjected to fire [¹⁴]. Additionally, used nonlinear FEA models to study the performance of axially restrained CES columns at elevated temperatures [¹⁵, ¹⁶].

Experimental studies are generally the most reliable way to examine the behavior of CFST and CES columns. However, there are generally only a few parameters that may be used in experimental design, which results in a limited number of specimens [¹⁷]. Researchers from all around the world have been paying close attention to models based on Artificial Intelligence (AI), particularly in Civil engineering problems. Many studies have highlighted the potential of ML techniques for predicting the properties and behavior of structural members [¹⁸, ¹⁹, ²⁰]. Extensive AI-based research has explored the behavior of CFST columns under various conditions. For example, utilized ANN to model the relationship between fire resistance and load-deformation in CFST columns with different dimensions and parameters [²¹, ²²]. Additionally, predicted the load-bearing capacity of CFST columns under axial loads using ANN models [²³]. Applied ANN to estimate the fire resistance of axially-loaded CES columns made from high-strength concrete. Their extensive parametric analysis identified seven inputs, three outputs, and two hidden layers for the ANN, resulting in a high determination coefficient (R2) of 0.999. However, research specifically focused on predicting the behavior of CES columns using AI techniques is still limited [²⁴, ²⁵, ²⁶, ²⁷, ²⁸, ²⁹, ³⁰].

Buildings exposed to high temperatures, particularly during fires, face significant risks, making fire resistance a critical design consideration. Concrete Encased Steel (CES) columns, composed of concrete, stirrups, longitudinal reinforcements, and encased steel sections, are increasingly used in high-rise buildings due to their superior mechanical properties under normal and elevated temperatures. CES columns offer enhanced ductility, shear resistance, and compressive strength, and their concrete encasement significantly improves fire resistance by slowing steel heating.

Extensive research has explored fire-resistant composite columns, with much focus on Concrete Filled Steel Tubular (CFST) columns. Studies demonstrate that factors like fire duration and steel section ratios impact post-fire residual strength. CES columns, however, are gaining attention due to their resistance to buckling and the confinement they provide to internal concrete.

Recent research has advanced the understanding of CES columns under fire, utilizing both experimental and computational methods. Artificial Intelligence (AI) techniques, particularly Artificial Neural Networks (ANN), have shown promise in predicting column behavior under fire. While ANN models have been extensively applied to CFST columns, research specifically predicting CES column behavior using AI remains limited, highlighting a gap for further investigation.

A clear research gap exists in the development of computational models specifically designed to predict the ultimate load capacity of Steel Fiber Reinforced Concrete Encased Steel (CES) columns under elevated temperatures. While studies have explored the behavior of reinforced concrete columns in fire conditions, there is a lack of models tailored to CES columns with steel fiber reinforcement. The unique characteristics of steel fiber reinforcement combined with encasement demand focused investigation to accurately predict their load-bearing capacity at high temperatures. Addressing this gap is crucial for improving structural resilience and safety in fire-prone environments, highlighting the need for specialized research in this area. This study aims to fill this gap by introducing a novel model for predicting the ultimate load capacity of CES columns exposed to high temperatures.

2. MATERIALS AND METHODS

This study aims to develop the prediction model for the ultimate load of CES column after exposed to elevated temperature under axial load.

2.1. Experimental investigation

Forty CES columns underwent casting and experimental axial load testing. The columns were designed with a cross-sectional area of 230 mm by 230 mm and incorporated an I-section made from a 2 mm thick light gauge steel plate, measuring 150 mm by 150 mm by 650 mm, as shown in Figure 1. The properties of the light gauge plate were determined through testing steel coupons cut from all four faces of the column tube sections, following ASTM E8/E8M-09 standards for tension. A steel column mold measuring 230 mm × 230 mm was prepared to accommodate the I-section. The mold was filled with freshly prepared concrete after placing the I-section. Notably, few column samples were filled with conventional concrete (CC), while others were filled with SFRC. The concrete was thoroughly compacted, and air gaps were eliminated using a needle vibrator.

Figure 1
Cross-sectional view of I-section.

Table 1 contains a comprehensive overview of the column specimens

Table 1
Details of the column specimens.

S.NO	COLUMN-ID	CONCRETE GRADE (MPA)	SLENDERNESS RATIO	COLUMN DIMENSIONS (WIDTH × DEPTH × LENGTH) IN MILLIMETERS	DESCRIPTION
1	I Section-RT	--	4.33	150 × 150 × 650	I -Section without encased concrete at RT
2	I Section-80	--	4.33	150 × 150 × 650	I -Section without encased concrete subjected to 80°C
3	I Section-120	--	4.33	150 × 150 × 650	I -Section without encased concrete subjected to 120°C
4	I Section-200	--	4.33	150 × 150 × 650	I -Section without encased concrete subjected to 200°C
5	M20-PCC-RT	M20	4.33	230 × 230 × 650	M20 grade PCC unencased column subjected to RT
6	M30-PCC-RT	M30	4.33	230 × 230 × 650	M30 grade PCC unencased column subjected to RT
7	M40-PCC-RT	M40	4.33	230 × 230 × 650	M40 grade PCC unencased column subjected to RT
8	M20-PCC-80	M20	4.33	230 × 230 × 650	M20 grade PCC unencased column subjected to 80°C
9	M30-PCC-80	M30	4.33	230 × 230 × 650	M30 grade PCC unencased column subjected to 80°C
10	M40-PCC-80	M40	4.33	230 × 230 × 650	M40 grade PCC unencased column subjected to 80°C
11	M20-PCC-120	M20	4.33	230 × 230 × 650	M20 grade PCC unencased column subjected to 120°C
12	M30-PCC-120	M30	4.33	230 × 230 × 650	M30 grade PCC unencased column subjected to 120°C
13	M40-PCC-120	M40	4.33	230 × 230 × 650	M40 grade PCC unencased column subjected to 120°C
14	M20-PCC-200	M20	4.33	230 × 230 × 650	M20 grade PCC unencased column subjected to 200°C
15	M30-PCC-200	M30	4.33	230 x 230 x 650	M30 grade PCC unencased column subjected to 200°C
16	M40-PCC-200	M40	4.33	230 × 230 × 650	M40 grade PCC unencased column subjected to 200°C
17	M20-CC-RT	M20	4.33	230 × 230 × 650	M20 grade CC encased column subjected to RT
18	M30-CC-RT	M30	4.33	230 × 230 × 650	M30 grade CC encased column subjected to RT
19	M40-CC-RT	M40	4.33	230 × 230 × 650	M40 grade CC encased column subjected to RT
20	M20-CC-80	M20	4.33	230 × 230 × 650	M20 grade CC encased column subjected to 80°C
21	M30-CC-80	M30	4.33	230 × 230 × 650	M30 grade CC encased column subjected to 80°C
22	M40-CC-80	M40	4.33	230 × 230 × 650	M40 grade CC encased column subjected to 80°C
23	M20-CC-120	M20	4.33	230 × 230 × 650	M20 grade CC encased column subjected to 120°C
24	M30-CC-120	M30	4.33	230 × 230 × 650	M30 grade CC encased column subjected to 120°C
25	M40-CC-120	M40	4.33	230 × 230 × 650	M40 grade CC encased column subjected to 120°C
26	M20-CC-200	M20	4.33	230 × 230 × 650	M20 grade CC encased column subjected to 200°C
27	M30-CC-200	M30	4.33	230 × 230 × 650	M30 grade CC encased column subjected to 200°C
28	M40-CC-200	M40	4.33	230 × 230 × 650	M40 grade CC encased column subjected to 200°C
29	M20-SFRC-RT	M20	4.33	230 × 230 × 650	M20 grade SFRC encased column subjected to RT
30	M30-SFRC-RT	M30	4.33	230 × 230 × 650	M30 grade SFRC encased column subjected to RT
31	M40-SFRC-RT	M40	4.33	230 × 230 × 650	M40 grade SFRC encased column subjected to RT
32	M20-SFRC-80	M20	4.33	230 × 230 × 650	M20 grade SFRC encased column subjected to 80°C
33	M30-SFRC-80	M30	4.33	230 × 230 × 650	M30 grade SFRC encased column subjected to 80°C
34	M40-SFRC-80	M40	4.33	230 × 230 × 650	M40 grade SFRC encased column subjected to 80°C
35	M20-SFRC-120	M20	4.33	230 × 230 × 650	M20 grade SFRC encased column subjected to 120°C
36	M30-SFRC-120	M30	4.33	230 × 230 × 650	M30 grade SFRC encased column subjected to 120°C
37	M40-SFRC-120	M40	4.33	230 × 230 × 650	M40 grade SFRC encased column subjected to 120°C
38	M20-SFRC-200	M20	4.33	230 × 230 × 650	M20 grade SFRC encased column subjected to 200°C
39	M30-SFRC-200	M30	4.33	230 × 230 × 650	M30 grade SFRC encased column subjected to 200°C
40	M40-SFRC-200	M40	4.33	230 × 230 × 650	M40 grade SFRC encased column subjected to 200°C

• Note: M20,30,40-Grade of Concrete, I section-Light Gauge Cold Form Structural Steel, RT-Room Temperature, °C-Elevated Temperature, PCC-Plain Cement Concrete, SFRC-Steel Fibre Reinforced Concrete

To attain the desired strength, SFRC was carefully formulated using conceptual proportioning according to the IS: 10262–2009 guidelines. The compressive strength of HVFA concrete was experimentally determined following IS: 516–1959 standards. OPC 53 grade Coromandel king cement served as the binder, with a specific gravity of 3.15 and 0.98 loss of ignition. Locally sourced river sand and well-graded angular-shaped granite stone met IS: 383–1970 specifications for fine and coarse aggregates. To improve workability, Conplast 430 superplasticizer, accommodating with IS 2645:2003, was incorporated. The mix incorporated hooked-end steel fibers, adhering to ASTM A820-01 standards, at a volume fraction of 1.5%. Detailed specifications of these steel fibers are listed in Table 2.

Table 2
Details of the column specimens.

PROPERTIES	HOOKED-END
Density	7850 kg/m3
Tensile strength	1700 (MPa)
Elastic modulus	2.1 ×105 N/mm2
Specific gravity	7.9
Length	35 mm
Diameter	0.55 mm
Aspect ratio	65

Initially, fine and coarse aggregates were added to the concrete mixer and mixed for 2 minutes. Cement was then introduced and mixed for an additional 2 minutes while dry. Next, the required amount of steel fibers and water were added to the mixture. This blend was then combined with the aggregates and cement in the mixer and mixed for another 4 minutes. The fresh concrete was poured into 150 mm × 150 mm × 150 mm cube molds for compressive strength testing. After 24 hours of moist curing, the cubes were removed from the molds and submerged in a water tank for further curing. Compressive strength tests were conducted at 7, 14, and 28 days of curing, following the guidelines of IS: 516–1959.

After curing for 28 days, some of the column samples were placed in a furnace equipped with a loading system, air and fuel supply, and data logging capabilities. The furnace, featuring electrical heating coils embedded in refractory bricks, was used to heat the samples. These columns were exposed to temperatures of 80°C, 120°C, and 200°C for 6 hours, as shown in Figure 2. Temperature measurements were recorded with thermocouples. Once the heating period was complete, the samples were removed from the furnace, allowed to cool to room temperature, and then tested for compressive strength under axial load using a Universal Testing Machine (UTM) with a 2000 kN capacity, as depicted in Figure 3, Figure 4 shows the test setup. To ensure a consistent application of stress, the column specimen was positioned in the center of the loading platform. The determined ultimate load of the various column was presented in Table 3.

Figure 2
Columns specimen.

Figure 3
Furnace.

Figure 4
Test set-up.

Table 3
Ultimate load of the column.

COLUMN-ID	ULTIMATE LOAD (KN)	COLUMN	ULTIMATE LOAD (KN)
I-RT	137.21	30CC-80	827.11
I-80	135.96	40CC-80	1055.55
I-120	127.51	20CC-120	644.59
I-200	119.42	30CC-120	784.81
20PCC-RT	437.69	40CC-120	937.66
30PCC-RT	545.26	20CC-200	591.11
40PCC-RT	602.37	30CC-200	731.93
20PCC-80	422.66	40CC-200	832.61
30PCC-80	533.21	20SFRC-RT	881.11
40PCC-80	595.25	30SFRC-RT	1137.49
20PCC-120	410.25	40SFRC-RT	1277.32
30PCC-120	521.12	20SFRC-80	794.91
40PCC-120	582.98	30SFRC-80	1108.32
20PCC-200	389.48	40SFRC-80	1134.88
30PCC-200	493.35	20SFRC-120	755.41
40PCC-200	566.65	30SFRC-120	969.26
20CC-RT	721.36	40SFRC-120	1055.96
30CC-RT	876.75	20SFRC-200	763.57
40CC-RT	1150.25	30SFRC-200	891.26
20CC-80	688.47	40SFRC-200	986.41

• Note: 20, 30,40 - Grade of Concrete, CC-conventional concrete, SFRC-Steel Fiber Reinforced Concrete, 80,120, 200°C-Elevated Temperature.

2.2. Construction of prediction model

The various steps involved in the model development are as follows;

• Collection of Data: This process involves gathering data from multiple sources, such as open-source repositories and experimental results, and organizing it accordingly.

• Data preprocessing: Accurately organizing the collected data requires addressing any missing values and standardizing the dataset prior to model development.

• Selection of model: Algorithm like Linear Regression (LR), Extreme Gradient Boosting (XGB), Gradient Boost Regressor (GBR) and Vote regressor were utilized for the development of model. The model uses the training dataset.

• Evaluation of model: The models are assessed and compared using performance metrics such as the coefficient of determination (R²), Root Mean Square Error (RMSE), and Mean Absolute Error (MAE). The algorithm that performs best according to these metrics is then selected.

2.2.1. Machine Learning (ML) algorithms

2.2.1.1. Linear Regression (LR)

The LR primarily focuses on conditional probability. In linear regression, the predictor variable and dependent variable are linearly interrelated. The expression for the LR was given as;

(1)$$\text{Y}=\text{mx}+\text{c}+\text{e}$$

In this equation, ‘m’ indicates the slope of the line, ‘c’ is the intercept, and ‘e’ represents the error term.

2.2.1.2. Extreme Gradient Boosting (XGB)

XGB is an advanced machine learning algorithm that utilizes decision trees and gradient boosting techniques to make predictions from complex data. Developed by Tianqi Chen and Carlos Guestrin, XGB builds upon the traditional gradient boosting method by integrating several improvements. It addresses the errors from previous models to enhance overall accuracy. By incorporating regularization into its objective function and using second-order derivatives, XGB effectively reduces over fitting and improves computational efficiency. XGB is recognized for its speed and robustness compared to other machine learning algorithms. The formula used for predictions in XGB is:

(2)$${\widehat{y}}_i=\text{}{\displaystyle {\sum }_{i=1}^k{f}_t(x_i)}$$

f_t Signifies the k^th refers to the base model; ŷ_i i indicates the predicted value for the i^th model.

2.2.1.3. Gradient Boost Regressor (GBR)

Gradient boosting constructs models incrementally, similar to other boosting techniques [²⁵]. The GBR is a streamlined version of gradient boosting that includes three main components: the loss function, the weak learner, and an additive model [²⁶]. The core idea is to ensure that new base learners have the highest possible correlation with the negative gradient of the loss function for the entire ensemble. Although the loss function can be chosen flexibly, using the square-error loss function is common because it helps to address prediction errors progressively. The mathematical formulation for GBR is as follows:

(3)$$F(x)=\text{}{\displaystyle {\sum }_{m=1}^M{\gamma }_m{h}_m}\text{}(x)$$

h_m(x) represents the root functions.

2.2.1.4. Voting Regressor (VR)

Voting ensemble methods in machine learning involve using multiple models to improve overall system performance, rather than relying on a single model. This approach can be applied to both classification and regression problems by aggregating the predictions from several models. For regression tasks, the final output is determined by averaging the predictions of all models, resulting in what is known as a VR [³¹]. Two common techniques for combining predictions are Average Voting (AV) and Weighted Voting (WV). In AV, all models are given equal importance, which assumes each model is equally effective an assumption that may not hold true, especially with diverse techniques. WV assigns specific weights to each model, which can be either integer values, indicating the number of votes each model has, or floating-point numbers that total 1, reflecting the relative importance of each model.

2.2.2. Description of dataset

A dataset consisting of 243 concrete mix proportion which includes 40 concrete mix proportion experimentally used and remaining 203 data are collected from the existing literatures [³², ³³, ³⁴, ³⁵, ³⁶, ³⁷, ³⁸, ³⁹, ⁴⁰, ⁴¹, ⁴², ⁴³, ⁴⁴, ⁴⁵]. This dataset encompasses 12 input variables and 1 output variable for each model and their respective ranges can be found in Table 4. The input variables consist of the amounts of cement, fine aggregate, coarse aggregate, water, superplasticizer, fiber volume fraction, eccentricity, concrete compressive strength, ultimate load, duration of heating, and temperature. The output variable indicates the ultimate load that the column can support after being subjected to elevated temperatures.

Table 4
Variables.

VARIABLE	RANGE
Cement (kg/m3)	50–540
Fine aggregate (FA) (kg/m3)	594–992.6
Coarse aggregate (CA) (kg/m3)	932–1232
Superplasticizer (kg/m3)	0–32.2
Water (kg/m3)	146–228
Fibre (%)	0–3%
eccentricity	0.5–10
Ultimate load (kN)	40–1277.32
Compressive strength of concrete (MPa)	12.8–67.6
Duration of heating (hours)	0–6
Temperature (°C)	0–1200°C
Ultimate load (MPa)	22.81–49.05

3. MODEL BUILDING AND TRAINING

3.1. Model building

Preprocessing

Prior to being employed with the regression approach, the collected data needs to be pre-processed. The pre-processing step comprises multiple processes which includes feature selection, scaling and data selection. Some of the unwanted data were removed from the collected dataset during the feature selection process. The ML regression method gives the output by using only the selected features from the dataset. The min-max scaling is used for the normalization of raw data.

Regression Algorithms

The next step is to develop the regression model. The data, after preprocessing, is divided into training and testing sets, with 80% used for training and 20% for testing. The training set is employed to create the model, while the testing set assesses the model’s accuracy in predicting the column's ultimate load. The algorithms, including Linear Regression, XGB, GBR, and VR, are applied to the training data.

Model Training

The evaluation of the model's performance was carried out through implementation. The prediction of the column's ultimate load was framed as a regression problem using machine learning techniques. The model was trained using Python on a laptop equipped with an Intel® Core™ i7 processor and 16GB of RAM. Data analysis and model development were conducted on Google Colab using the Scikit-learn library, a popular open-source tool for machine learning.

3.2. Evaluation of model

To assess and compare the performance of the different models, metrics such as R2, RMSE, MSE, and MAE were utilized. These metrics helped identify the most accurate regression model for predicting the ultimate load of the encased column under elevated temperatures.

3.3. Statistical characteristics of the dataset

The connection between the input and output variables is depicted in Figure 5. A complex, non-linear relationship was observed between the ultimate load of the column and the input variables. Also, a negative association has been noted, meaning that a rise in one variable is associated with a fall in another. The study revealed a positive correlation between the ultimate load of the column and the following factors such as cement, coarse aggregate, compressive strength, temperature and fiber percentage. This implies that higher values of these factors will increase the column's ultimate load. Conversely, the ultimate load is inversely related to the quantities of fine aggregate, water, eccentricity, superplasticizer, and heating duration; thus, increasing any of these factors will decrease the ultimate load. It was found that the compressive strength of the concrete has the greatest influence on the ultimate load, with cement, coarse aggregate, and temperature following. Table 5 provides the statistical details of the dataset.

Figure 5
Illustrates the relationship between two variables.

Table 5
Statistical characteristics of the dataset.

VARIABLE	CEMENT	FINE AGGRE GATE	COARSE AGGRE GATE	WATER	ECCENTRI CITY	COMPRE SSIVE STRENGTH	SUPER PLASTI CIZER	DURATION OF HEATING	TEMPE RATURE	FIBER	ULTIMATE LOAD
UNIT	Kg/m3	Kg/m3	Kg/m3	Kg/m3	-	Kg/m3	Kg/m3	hrs.	°C	%	(kN)
Count	243	243	243	243	243	243	243	243	243	243	243
Mean	282.22	730	678.47	186.20	1.163	31.6	8.15	2.49	188.39	68.28	261.26
Std.	138.66	142.83	481.46	35.58	2.276	10.84	7.89	1.12	225.28	93.21	282.66
Min.	50	2.49	0	0	0	4.6	0	1	-40	0	0
25%	190	659.90	21.2	168	0.4	23.5	0	1.5	21	3	45.71
50%	360	755.80	932	192	0.5	32.1	7.5	2	120	28	105.42
75%	391	833	978.4	198	1	41.5	11.6	3	200	90	436.34
Max.	540	992.6	1232	228	12	67.6	32.2	4	1200	365	1277.32

Figure 6 displayed a visual representation of histogram obtained for the data. The visualization aids in identifying the most suitable method for achieving the best fit in machine learning techniques. The distribution of the variables is normal. Consequently, it is feasible to observe the efficiency of the learning algorithm can be facilitated.

Figure 6
Histogram plot for the variables.

4. IMPLEMENTATION AND RESULT

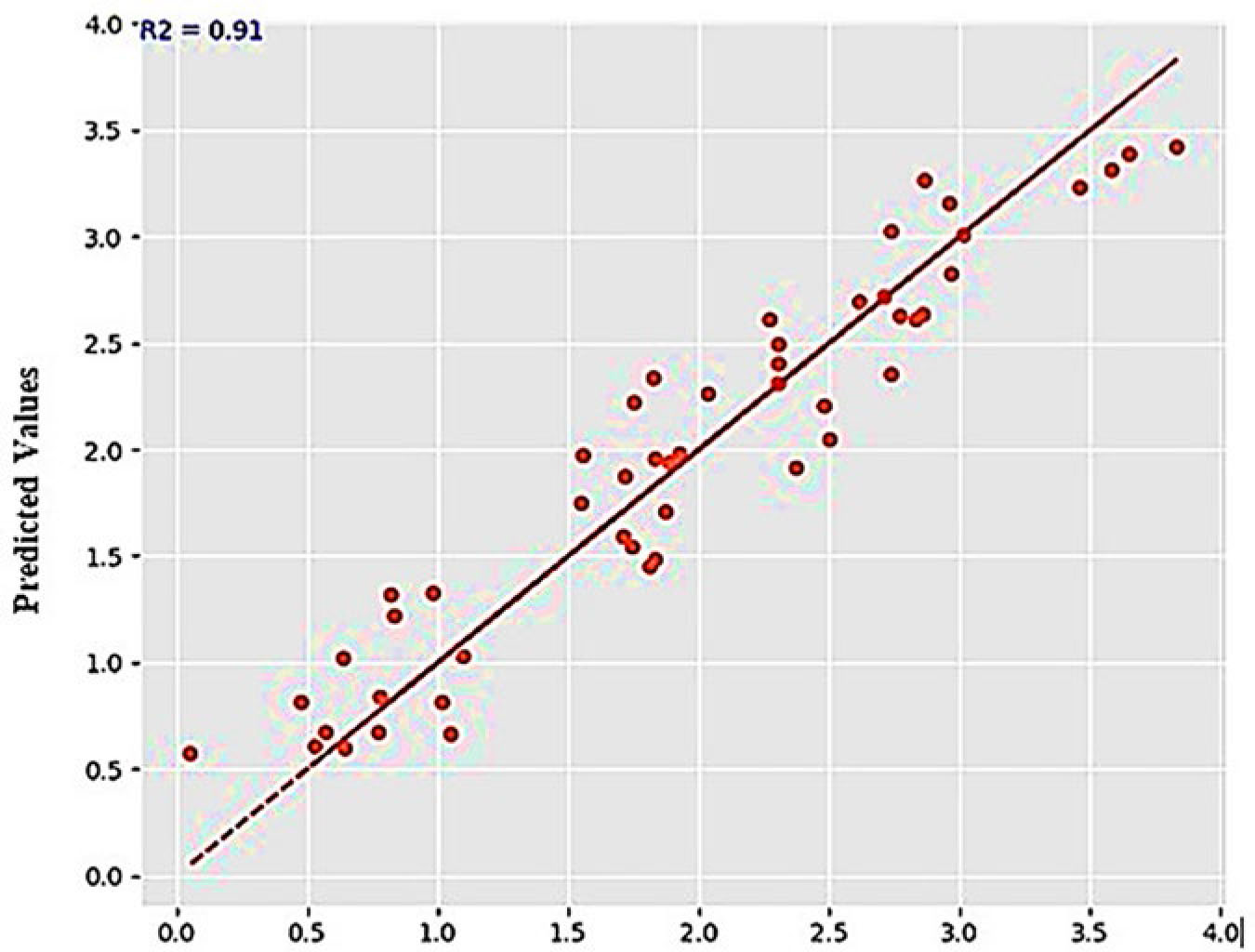
In predicting the ultimate load of the CES column, the Linear Regression (LR) model achieved a learning rate of 0.091, with RMSE, MSE, and MAE values of 0.28 kN, 0.08 kN, and 0.24 kN, respectively. Figure 7 compares the experimental ultimate load with the LR-predicted ultimate load.

Figure 7
Actual and predicated compressive strength using LR.

Table 6 provided the parameters for the GBR. In the prediction of the ultimate load, the GBR model achieving a 0.9 performance at a learning rate of 0.1, with RMSE, MSE and MAE of 0.26 kN, 0.09 kN and 0.26 kN respectively. Figure 8 compares and illustrates the experimental ultimate load and the GBR predicted ultimate load.

Table 6
Parameters for GBR.

PARAMETERS	VALUE
Learning rate	0.1–1
n-estimates	1000
Max.depth	6

Figure 8
Actual and predicated compressive strength using GBR.

Table 7 provided the parameters for the XGB. In the prediction of the ultimate load of CES column after exposed to elevated temperature, the XGB model performed best, achieving a 0.94 at a learning rate of 0.5 and RMSE, MSE, and MAE of 0.15 kN, 2.3 kN, and 11.68 kN, respectively. Figure 9 compares and displays the experimental ultimate load and the XGB predicted ultimate load.

Table 7
Parameters for GBR.

PARAMETERS	VALUE
Learning rate	0.1–1
n-estimates	500
Max.depth	5

Figure 9
Actual and predicated compressive strength using XGB.

Table 8 provided parameters for the VR. The VR model achieved the best performance of 0.93 at the learning rate of 0.05 in the prediction of ultimate load with an RMSE, MSE and MAE of 0.15 kN, 2.3 kN and 11.68 kN respectively. Figure 10 compares and displays the experimental ultimate load and the VR anticipated ultimate load

Table 8
Parameters for VR.

PARAMETERS	VALUE
Learning rate	0.01–1
depth	7
Random seed	42

Figure 10
Actual and predicated compressive strength using VR algorithm.

The Figures 11, 12, 13, 14 compare the R², RMSE, MSE and MAE values of the various models. XGB (Extreme Gradient Boosting) achieved a high R² of 0.94, indicating a strong fit to the data. However, its higher MSE of 2.3 might suggest it was more prone to outliers or larger errors in certain predictions. The higher MAE value of 11.68 also indicates high error in prediction. VR outperformed the other models with an impressive R² of 0.98, the highest among all algorithms. Additionally, it demonstrated the lowest RMSE of 0.09, indicating superior accuracy compared to the other algorithms. The MSE of 0.85 and MAE of 6.66 were also notably lower than those of the other algorithm, suggesting VR is the better overall performance in predicting ultimate load under elevated temperatures for the encased steel fiber-reinforced columns. The other algorithm namely LR, GBR, and VR also perform well, but they are not as accurate as the VR algorithm. The LR model has the lowest R² value (0.91), but it has a relatively low MAE (0.24) and MSE (0.08) values. The GBR model has a slightly higher R² value (0.9) than the LR model, but it has higher MAE (0.26) and MSE (0.09) values. Therefore, based on these results, the VR algorithm stands out as the better-performing model for this particular prediction task, offering higher accuracy and a better fit to the data compared to LR, GBR and XGB. Overall, the VR algorithm is the best performing model for predicting the ultimate load of encased steel fiber reinforced columns subjected to elevated temperature. It is able to fit the data better and make more accurate predictions than the other models. Table 9 presents the performance metrics of various ML models in the prediction of compressive strength. It was observed that the VR algorithm can learn the complex relationships between the different variables that affect the ultimate load of the columns, such as the temperature, the concrete grade, etc. The similar effect was already recorded [⁴⁶, ⁴⁷].

Figure 11
R² value of various models.

Figure 12
RMSE value of various models.

Figure 13
MSE value of various models.

Figure 14
MAE value of various models.

Table 9
Performance values of various models on testing data.

ALGORITHM	R2	RMSE	MSE	MAE
LR	0.91	0.28	0.08	0.24
GBR	0.9	0.26	0.09	0.26
XGB	0.94	0.15	2.3	11.68
VR	0.98	0.09	0.85	6.66

5. CONCLUSIONS

This study aimed to estimate the ultimate load of Steel Fiber Reinforced Encased Steel columns under elevated temperatures, crucial for ensuring structural resilience during fire incidents. Traditional methods for determining concrete properties are time-intensive, leading to the adoption of Machine Learning (ML) for quicker and more efficient predictions. Models such as Linear Regression (LR), Extreme Gradient Boosting (XGB), Gradient Boost Regressor (GBR), and Voting Regressor (VR) were developed to predict the ultimate load of these columns under fire conditions. The study's key findings highlight the effectiveness of these ML models in enhancing predictive accuracy and efficiency, particularly under elevated temperatures.

• The correlation analysis revealed intricate nonlinear relationships between input and output variables, underscoring the complexity of the studied system.

• Model performance evaluation, utilizing R-squared (R²), Root Mean Square Error (RMSE), and Mean Absolute Error (MAE) showcased varied strengths among the models.

• The XGB model demonstrated robust predictive capabilities with an R² of 0.94 but displayed higher MSE and MAE, suggesting vulnerability to outliers.

• The Voting Regressor (VR) emerged as the top-performing model, with an impressive R² of 0.98 and recording the lowest RMSE, MSE, and MAE. This underscores its superior accuracy compared to LR and GBR.

• The Voting Regressor algorithm demonstrated the highest accuracy in predicting the ultimate load of encased columns under elevated temperatures, with high R² and minimal error metrics, marking a significant advancement in applying Machine Learning techniques to enhance structural integrity and safety in fire-prone environments.

6. ACKNOWLEDGMENTS

Thanks for SRM Institute of Science and Technology, Kattankulathur, for providing lab facilities to this research

7. BIBLIOGRAPHY

• ^[1] ZENG, L., XIAO, Y., CHEN, Y., et al, “Seismic damage evaluation of concrete-encased steel frame-reinforced concrete core tube buildings based on dynamic characteristics”, Applied Sciences, v. 7, n. 4, pp. 314, 2017. doi: http://doi.org/10.3390/app7040314.
  » https://doi.org/10.3390/app7040314
• ^[2] ZENG, L., CUI, Z., XIAO, Y., et al, “Cyclical behavior of concrete-encased composite frame joints with high strength concrete”, Advances in Materials Science and Engineering, v. 2015, pp. 1–13, 2015. doi: http://doi.org/10.1155/2015/873162.
  » https://doi.org/10.1155/2015/873162
• ^[3] ZENG, L., XIAO, Y., CHEN, J., et al, “Quasi-static cyclic test on a concrete-encased frame-reinforced concrete tube building mode”, Shock and Vibration, v. 2018, n.1, pp. 5643872, 2018. doi: http://doi.org/10.1155/2018/5643872.
  » https://doi.org/10.1155/2018/5643872
• ^[4] HUO, J., ZENG, X., XIAO, Y., “Cyclic behaviours of concrete-filled steel tubular columns with pre-load after exposure to fire”, Journal of Constructional Steel Research, v. 67, n. 4, pp. 727–739, 2011. doi: http://doi.org/10.1016/j.jcsr.2010.11.005.
  » https://doi.org/10.1016/j.jcsr.2010.11.005
• ^[5] CHEN, Y., WANG, K., HE, K., et al, “Compressive behavior of CFRP-confined post heated square CFST stub columns”, Thin-walled Structures, v. 127, pp. 434–445, 2018. doi: http://doi.org/10.1016/j.tws.2018.02.012.
  » https://doi.org/10.1016/j.tws.2018.02.012
• ^[6] WANG, J., QIU, W.J., KONG, S.C., et al, “Investigation of the axial compressive behaviour of CFRP-confined circular CFST stub columns with inner latticed steel angles”, Composite Structures, v. 280, pp. 114895, 2022. doi: http://doi.org/10.1016/j.compstruct.2021.114895.
  » https://doi.org/10.1016/j.compstruct.2021.114895
• ^[7] XIONG, C.N., SHAO, Y.B., TONG, L.W., et al, “Static strength of CFRP-strengthened preloaded circular concrete-filled steel tube stub column columns. Part II: theoretical and numerical analysis”, Thin-walled Structures, v. 184, pp. 110547, 2023. doi: http://doi.org/10.1016/j.tws.2023.110547.
  » https://doi.org/10.1016/j.tws.2023.110547
• ^[8] MENG, F., ZHU, M.C., MOU, B., et al, “Residual strength of steel-reinforced concrete-filled square steel tubular (SRCFST) stub columns after exposure to ISO-834 standard fire”, International Journal of Steel Structures, v. 19, n. 3, pp. 850–866, 2019. doi: http://doi.org/10.1007/s13296-018-0174-z.
  » https://doi.org/10.1007/s13296-018-0174-z
• ^[9] YANG, X., TANG, C., CHEN, Y., et al, “Compressive behavior of steel-reinforced concrete-filled square steel tubular stub columns after exposure to elevated temperature”,Engineering Structures, v. 204, pp. 110048, 2020. doi: http://doi.org/10.1016/j.engstruct.2019.110048.
  » https://doi.org/10.1016/j.engstruct.2019.110048
• ^[10] YAN, J.B., WANG, T., DONG, X., “Compressive behaviours of circular concrete-filled steel tubes exposed to low-temperature environment”,Construction & Building Materials, v. 245, pp. 118460, 2020. doi: http://doi.org/10.1016/j.conbuildmat.2020.118460.
  » https://doi.org/10.1016/j.conbuildmat.2020.118460
• ^[11] YANG, X., LI, Z., CHEN, Y., et al, “Performance of concrete encased steel stub columns after exposure to high temperatures”,Journal of Constructional Steel Research, v. 187, pp. 106934, 2021. doi: http://doi.org/10.1016/j.jcsr.2021.106934.
  » https://doi.org/10.1016/j.jcsr.2021.106934
• ^[12] MALHOTRA, H.L., STEVENS, R.F., “Fire resistance of encased steel stanchions”,Proceedings of the Institution of Civil Engineers, v. 27, n. 1, pp. 77–98, 1964. doi: http://doi.org/10.1680/iicep.1964.10371.
  » https://doi.org/10.1680/iicep.1964.10371
• ^[13] YU, J.T., LU, Z.D., XIE, Q., “Nonlinear analysis of SRC columns subjected to fire”,Fire Safety Journal, v. 42, n. 1, pp. 1–10, 2007. doi: http://doi.org/10.1016/j.firesaf.2006.06.006.
  » https://doi.org/10.1016/j.firesaf.2006.06.006
• ^[14] HUANG, Z.F., TAN, K.H., TOH, W.S., et al, “Fire resistance of composite columns with embedded I-section steel: effects of section size and load level”,Journal of Constructional Steel Research, v. 64, n. 3, pp. 312–325, 2008. doi: http://doi.org/10.1016/j.jcsr.2007.07.002.
  » https://doi.org/10.1016/j.jcsr.2007.07.002
• ^[15] CORREIA, A.J.M., RODRIGUES, J.P.C., “Fire resistance of partially encased steel columns with restrained thermal elongation”,Journal of Constructional Steel Research, v. 67, n. 4, pp. 593–601, 2011. doi: http://doi.org/10.1016/j.jcsr.2010.12.002.
  » https://doi.org/10.1016/j.jcsr.2010.12.002
• ^[16] ALEX, A.G., JOSE, P.A., ANTONY, M.R., et al, “The effect of partial replacement of cement with Diatomaceous Earth (DE) and Polypropylene Fibers (PPF) on fresh, hardened, and durability properties of concrete”,International Journal of Concrete Structures and Materials, v. 18, n. 1, pp. 24, 2024. doi: http://doi.org/10.1186/s40069-024-00666-z.
  » https://doi.org/10.1186/s40069-024-00666-z
• ^[17] YOUNG, B., ELLOBODY, E., “Performance of axially restrained concrete encased steel composite columns at elevated temperatures”,Engineering Structures, v. 33, n. 1, pp. 245–254, 2011. doi: http://doi.org/10.1016/j.engstruct.2010.10.019.
  » https://doi.org/10.1016/j.engstruct.2010.10.019
• ^[18] QU, X., CHEN, Z., SUN, G., “Experimental study of rectangular CFST columns subjected to eccentric loading”,Thin-walled Structures, v. 64, pp. 83–93, 2013. doi: http://doi.org/10.1016/j.tws.2012.12.006.
  » https://doi.org/10.1016/j.tws.2012.12.006
• ^[19] AMANI, J., MOEINI, R., “Prediction of shear strength of reinforced concrete beams using adaptive neuro-fuzzy inference system and artificial neural network”,Scientia Iranica, v. 19, n. 2, pp. 242–248, 2012. doi: http://doi.org/10.1016/j.scient.2012.02.009.
  » https://doi.org/10.1016/j.scient.2012.02.009
• ^[20] NGUYEN, H.Q., LY, H.B., TRAN, V.Q., et al, “Optimization of artificial intelligence system by evolutionary algorithm for prediction of axial capacity of rectangular concrete filled steel tubes under compression”,Materials, v. 13, n. 5, pp. 1205, 2020. doi: http://doi.org/10.3390/ma13051205. PubMed PMID: 32156033.
  » https://doi.org/10.3390/ma13051205
• ^[21] DAO, D.V., NGUYEN, N.L., LY, H., et al, “Cost-effective approaches based on machine learning to predict dynamic modulus of warm mix asphalt with high reclaimed asphalt pavement”,Materials, v. 13, n. 15, pp. 3272, 2020. doi: http://doi.org/10.3390/ma13153272. PubMed PMID: 32717910.
  » https://doi.org/10.3390/ma13153272
• ^[22] AL-KHALEEFI, A.M., TERRO, M.J., ALEX, A.P., et al, “Prediction of fire resistance of concrete filled tubular steel columns using neural networks”,Fire Safety Journal, v. 37, n. 4, pp. 339–352, 2002. doi: http://doi.org/10.1016/S0379-7112(01)00065-0.
  » https://doi.org/10.1016/S0379-7112(01)00065-0
• ^[23] WANG, Y., LIU, Z.Q., ZHANG, M., “Prediction of mechanical behavior of concrete filled steel tube structure using artificial neural network”,Applied Mechanics and Materials, v. 368, pp. 1095–1098, 2013. doi: http://doi.org/10.4028/www.scientific.net/AMM.368-370.1095.
  » https://doi.org/10.4028/www.scientific.net/AMM.368-370.1095
• ^[24] DU, Y., CHEN, Z., ZHANG, C., et al, “Research on axial bearing capacity of rectangular concrete-filled steel tubular columns based on artificial neural networks”,Frontiers of Computer Science, v. 11, n. 5, pp. 863–873, 2017. doi: http://doi.org/10.1007/s11704-016-5113-6.
  » https://doi.org/10.1007/s11704-016-5113-6
• ^[25] LI, S., LIEW, J.Y.R., XIONG, M.-X., “Prediction of fire resistance of concrete encased steel composite columns using artificial neural network”,Engineering Structures, v. 245, pp. 112877, 2021. doi: http://doi.org/10.1016/j.engstruct.2021.112877.
  » https://doi.org/10.1016/j.engstruct.2021.112877
• ^[26] AMERICAN SOCIETY FOR TESTING AND MATERIALS, ASTM E8/E8M-09 Standard Test Methods for Tension Testing of Metallic Materials, West Conshohocken, ASTM, 2009. doi: http://doi.org/10.1520/E0008_E0008M-09.
  » https://doi.org/10.1520/E0008_E0008M-09
• ^[27] BUREAU OF INDIAN STANDARDS, IS 10262-2019 Concrete Mix Design as Per IS Code, New Delhi, BIS, 2019.
• ^[28] BUREAU OF INDIAN STANDARDS, IS 516:1959 (Reaffirmed 2004) Methods of Test for Strength of Concrete, Amendment No 2, New Delhi, BIS, 1993.
• ^[29] BUREAU OF INDIAN STANDARDS, IS 12269:2015 Specification for 53 Grade Cement Ordinary Portland Cement, New Delhi, BIS, 2015.
• ^[30] BUREAU OF INDIAN STANDARDS, IS 383:1970, Specification for Coarse and Fine Aggregates from Natural Sources for Concrete, New Delhi, BIS, 1970.
• ^[31] BUREAU OF INDIAN STANDARDS, IS 2645:2003 Integral Waterproofing Compounds for Cement Mortar and Concrete – Specification, New Delhi, BIS, 2003.
• ^[32] AMERICAN SOCIETY FOR TESTING AND MATERIALS, ASTM A820-01 Standard Specification for Steel Fibers for Fiber-Reinforced Concrete, West Conshohocken, ASTM, 2001. doi: http://doi.org/10.1520/A0820-01.
  » https://doi.org/10.1520/A0820-01
• ^[33] KILIMCI, Z.H., “Ensemble regression-based gold price (XAU/USD) prediction”,Journal of Emerging Computer Technologies., v. 2, n. 1, pp. 7–12, 2022.
• ^[34] AL-NAQEEB, F., AL-THAIRY, H., “The behavior of reinforced concrete columns exposure to eccentric loads at high temperature”,Journal of Physics: Conference Series, v. 1895, n. 1, pp. 012055, 2021. doi: http://doi.org/10.1088/1742-6596/1895/1/012055.
  » https://doi.org/10.1088/1742-6596/1895/1/012055
• ^[35] BERRY, M., JOHNSON, J., MCDEVITT, K., “Effect of cold temperatures on the behavior and ultimate capacity of GFRP-reinforced concrete beams”,Cold Regions Science and Technology, v. 136, pp. 9–16, 2017. doi: http://doi.org/10.1016/j.coldregions.2017.01.003.
  » https://doi.org/10.1016/j.coldregions.2017.01.003
• ^[36] CHEN, J., YOUNG, B., “Design of high strength steel columns at elevated temperatures”,Journal of Constructional Steel Research, v. 64, n. 6, pp. 689–703, 2008. doi: http://doi.org/10.1016/j.jcsr.2007.09.004.
  » https://doi.org/10.1016/j.jcsr.2007.09.004
• ^[37] ELLOBODY, E., YOUNG, B., “Investigation of concrete encased steel composite columns at elevated temperatures”,Thin-walled Structures, v. 48, n. 8, pp. 597–608, 2010. doi: http://doi.org/10.1016/j.tws.2010.03.004.
  » https://doi.org/10.1016/j.tws.2010.03.004
• ^[38] NEMATZADEH, M., SHAHMANSOURI, A.A., FAKOOR, M., “Post-fire compressive strength of recycled PET aggregate concrete reinforced with steel fibers: optimization and prediction via RSM and GEP”,Construction & Building Materials, v. 252, pp. 119057, 2020. doi: http://doi.org/10.1016/j.conbuildmat.2020.119057.
  » https://doi.org/10.1016/j.conbuildmat.2020.119057
• ^[39] QIAN, Z.H., TAN, K.H., BURGESS, I.W., “Behavior of steel beam-to-column joints at elevated temperature: experimental investigation”,Journal of Structural Engineering, v. 134, n. 5, pp. 713–726, 2008. doi: http://doi.org/10.1061/(ASCE)0733-9445(2008)134:5(713).
  » https://doi.org/10.1061/(ASCE)0733-9445(2008)134:5(713)
• ^[40] SAID, M., ABD EL-AZIM, A.A., ALI, M.M., et al, “Effect of elevated temperature on axially and eccentrically loaded columns containing Polyvinyl Alcohol (PVA) fibers”,Engineering Structures, v. 204, pp. 110065, 2020. doi: http://doi.org/10.1016/j.engstruct.2019.110065.
  » https://doi.org/10.1016/j.engstruct.2019.110065
• ^[41] KEDIR, A., GAMACHU, M., ALEX, A.G., “Cement-based graphene oxide composites: a review on their mechanical and microstructure properties”,Journal of Nanomaterials, v. 2023, n. 1, pp. 6741000, 2023. doi: http://doi.org/10.1155/2023/6741000.
  » https://doi.org/10.1155/2023/6741000
• ^[42] KEPRATE, A., RATNAYAKE, R.C., “Using gradient boosting regressor to predict stress intensity factor of a crack propagating in small bore piping”,In: Proceedings of the 2017 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), pp. 1331–1336, 2017. doi: http://doi.org/10.1109/IEEM.2017.8290109.
  » https://doi.org/10.1109/IEEM.2017.8290109
• ^[43] LU, H., MAZUMDER, R., “Randomized gradient boosting machine”,SIAM Journal on Optimization, v. 30, n. 4, pp. 2780–2808, 2020. doi: http://doi.org/10.1137/18M1223277.
  » https://doi.org/10.1137/18M1223277
• ^[44] NGUYEN-SY, T., WAKIM, J., TO, Q., et al, “Predicting the compressive strength of concrete from its compositions and age using the extreme gradient boosting method”,Construction & Building Materials, v. 260, pp. 119757, 2020. doi: http://doi.org/10.1016/j.conbuildmat.2020.119757.
  » https://doi.org/10.1016/j.conbuildmat.2020.119757
• ^[45] SAKAI, K., SHEIKH, S.A., “What do we know about confinement in reinforced concrete columns: a critical review of previous work and code provisions”,ACI Structural Journal, v. 86, n. 2, pp. 192–207, 1989.
• ^[46] ULAGAMBIKA, P., MURUGAN, M., “Performance of fire damaged cement and geopolymer concrete slabs retrofitted with BFRP laminates under static loading”,Matéria, v. 29, n. 2, e20240015, 2024. doi: http://doi.org/10.1590/1517-7076-rmat-2024-0015.
  » https://doi.org/10.1590/1517-7076-rmat-2024-0015
• ^[47] SILVA, E., SOUZA, L., MEIRELLES, P., et al, “Minimum squares method in the use of rotation moment curves in the analysis of semi-rigid plane frames”,Matéria, v. 28, e20220285, 2023. doi: http://doi.org/10.1590/1517-7076-rmat-2022-0285.
  » https://doi.org/10.1590/1517-7076-rmat-2022-0285

Publication Dates

• Publication in this collection
  31 Jan 2025
• Date of issue
  2024

History

• Received
  06 Sept 2024
• Accepted
  17 Oct 2024