Models for estimating yacon leaf area

Modelos de determinação indireta da área foliar em yacon

ABSTRACT

The recent exploration of yacon demands scientific information for improving the crop production technology. This study aimed to set a leaf area estimate model for yacon plants, using non-destructive measurements of leaf length (L) and/or width (W). Sixty-four representative yacon plants were randomly selected in an experimental field during the full vegetative growth. One thousand leaves of various sizes were taken from those plants for setting and validating a model. The logarithmic model best fitted this purpose, the result of multiplying length by width being used as independent variable. Yacon leaf area can be determined with high precision and accuracy by LA_LW = (-27.7418 + (3.9812LW / ln LW ) , disregarding the leaf size.

Keywords: Smallanthus sonchifolius; leaf size; mathematical modeling.

RESUMO

A exploração recente de yacon gera demanda de informações científicas que impulsionem o desenvolvimento de tecnologias específicas de manejo e condução da lavoura. Neste escopo, visando contribuir nos campos fitotécnico e fisiológico, o presente trabalho objetivou ajustar um modelo de estimação de área foliar em batata yacon, usando medidas não destrutivas do comprimento (C) e/ou largura (L) de suas folhas. Para tal, 64 plantas representativas da cultura foram coletadas ao acaso, em um campo experimental em pleno crescimento vegetativo. Dessas plantas, 1000 folhas de diversos tamanhos foram tomadas para a construção e posterior validação do modelo construído. O modelo logarítmico foi o que apresentou melhor ajuste considerando como variável independente o produto do comprimento pela largura da folha. Desta forma, encontrou-se que a área foliar em batata yacon, independente do tamanho da folha, pode ser determinada com altas precisões e acurácia, através do estimador AF_CL = (-27,7418 + (3,9812CL / ln CL ) .

Palavras-chave: Smallanthus sonchifolius; dimensão foliar; modelagem matemática.

Since the world's population is searching for healthy eating habits, the consumption of natural, hypo caloric and gluten-free foods has been increasing. In this context, yacon or "diet potato" has attracted commercial interest in the world due to its promising effects on health and has been showing up in the market. Among these effects, we can highlight diabetes control, intestinal regulation and increasing satiety (Manrique & Párraga, 2005; Santana & Cardoso, 2008).

Yacon potato (Smallanthus sonchifolius), species of Asteraceae family, is from the Andes, and found from Colombia and Venezuela to the northwestern Argentina (Seminário et al., 2003). The plant consumption has been noticed, significantly, since the mid-2000s.

In Brazil, the species was introduced by Japanese immigrants, from 1989-1990 in Capão Bonito, São Paulo State, and more recently in mountain areas in the state of Espírito Santo and Rio de Janeiro (Seminario et al., 2003; Moscatto et al., 2004; Santana & Cardoso, 2008).

Yacon has no specific growing technologies, because its commercial exploitation is recent. This is the main obstacle for its development. Information related to these technologies is rare in the phytotechnical area, only some notes taken by Vilhena et al. (2000) and Santana & Cardoso (2008) can be found. This fact justifies that more studies are necessary on the growing and development of this species. Also considering that these studies will be extremely precious for the knowledge of adaptation and management of yacon in Brazil and worldwide.

One of the essential morphologic variables which influence plant growth is the leaf area. From this variable, useful leaf area index (LAI) can be determined in agronomic studies (Blanco & Folegatti, 2005). This evaluation is indispensable for the evaluation of cultivation practices, such as plant density, fertilization, irrigation, pruning and pesticides application (Favarin et al., 2002).

The leaf area evaluation has been carried out directly through digital integrators and indirectly, through associative mathematical models (Silva et al., 2011). Despite high precision, such integrators are costly and most of the times restrict to the laboratory destructive evaluation of plant material under study.

On the other hand, the use of mathematical models which associate leaf area with measures of the leaf blade can be as accurate as the use of integrators and also can allow measurements, at low cost, during different phenological stages of the crop in the field (Lima et al., 2008, Fialho et al., 2011; Pompelli et al., 2012).

However, the right choice of the models mentioned must go through a detailed statistical study in order to guarantee that the selected equation to estimate the leaf area is practical, simple and accurate (Fialho et al., 2011).

This study aimed to determine a regression equation which expresses, accurately, the functional relationship between the leaf area and the measurements of the yacon leaf blade. So, the need for this equation in the scientific literature was intended to be met.

MATERIAL AND METHODS

The experiment was carried out at Instituto Federal do Espírito Santo (Federal Institute of Espírito Santo State, IFES), located in Alegre, Espírito Santo State. The local climate is AW- rainy tropical region, dry winter, according to Köppen classification. The annual average temperature is 23.1°C, with average annual rainfall 1166 mm (INMET, 2014).

The soil was submitted to chemical analysis, presenting the following characteristics in the 0-20 cm layer: pH= 5.95 in water; P_Mehlich1, K, Ca, Mg, Al, H + Al, sum of basis, effective CEC and CEC total, respectively, were: 0.176; 1.30; 0.49; 0.0; 1.80; 1.97; 1.97 and 3.77 cmol_c/dm³; 52.25% basis saturation; 0.0% aluminum saturation; 1.4 dag/kg organic matter; S, B, Fe, Cu, Mn and Zn, respectively, were: 0.0297; 0.0007; 0.0637; 0.0012; 0.0565 and 0.0081 cmol_c/dm³.

Planting was carried out at May 14, 2014; using seedlings of yacon, grown in tubes, in the nursery of the Centro de Ciências Agrárias da Universidade Federal do Espírito Santo (Agricultural Sciences Center of Espirito Santo State University, CCA/UFES). The seedlings were transplanted 32 days after emergence.

The experiment evaluation was carried out 125 days after seedling transplanting, 64 yacon plants being collected, at random in a representative way, which showed average of 15.63 leaves/plant, totalizing 1000 leaves of several sizes, all in the vegetative growth stage. The authors excluded from this accounting and, therefore from this study, unopened leaves and the ones which were damaged, mechanically or by pests.

After plant collection in the experimental field, the leaves were separated, scrambled, packed in plastic bags, and taken to the laboratory of Fitotecnia (Laboratory of Plant Sciences), CCA/UFES, where the measurements of leaf length and width were carried out, with the aid of a millimetric ruler.

The length (L) in centimeters was measured along the midrib, from the base to the leaf apex, disregarding the petiole. The width (W) in centimeters was measured perpendicular to the midrib, obtained from one end to the other, where the highest value was considered, both measurements used centimeters (cm) as unity (Figure 1).

Figure 1
Yacon leaf presenting length and width measures (folha de yacon, com as dimensões no limbo foliar, onde foi realizada a medida de comprimento e largura). Alegre-ES, UFES, 2014.

Then, the observed leaf area (LA_obs ) was determined for each leaf using the Licor Area Meter 3100 C (LI-3100 C Area Meter), calibrated according to the manufacturer recommendations.

The regression models were generated from 606 observations taken, at random, of the blades mentioned {LA as linear function of L, W, L+W, LW, (L+W)/2 and (LW)/2}, the others 394 being reserved for the validation study of the chosen model.

The statistical criteria to evaluate the best regression model were based on: a) the variance analysis of the regression: significant F-test for the regression (α=0.01); b) significant Student's t-test for the model parameters under the assumption: H0 : β i = 0 vs. H0 : β i ≠ 0 (α=0.01); c) adjusted coefficient of determination for degrees of freedom (R_a ²⁾; d) standard error for the estimates (SE) and e) residuals dispersion pattern (Antunes et al., 2008).

The SE estimate was obtained through the following estimator:

During validation, the authors used 394 observations of the leaf blades previously reserved; n= 394.

In order to verify the adequacy study of the model chosen in the previous step, the authors, initially, adjusted to a new simple linear regression model without intercept (LRMWI), relating to the leaf area values measured by the leaf area integrator in the 394 observations (LA_obs ) with the predictives by the regression model adopted (LA_est ). Thus:

Y_i = β X_i + ε_i

Where: Y_i represents the i^th leaf obtained by the regression model chosen - LA_est ; β, angular coefficient or slope; X_i corresponding to the i^th leaf observed - LA_obs , and ε_i , corresponding to the random error associated to each observation. Parameter β was estimated by the ordinary least-square method. For LRMWI, the following assumption was tested: H₀: β_i = 1 vs. H₀: β_i ≠ 1 (α=0.01), which corresponds to the equivalence between the leaf area measurement, predicted by the equation adopted and the observed, measured in the laboratory.

The existence of a linear dependence between observed and estimated values related to its magnitude and direction was investigated through Pearson correlation (ρ), providing an idea of the model accuracy.

The error related to the model chosen was evaluated as "average relative error" (ARE%), average value of differences (in module) between the values of estimated and observed leaf area, expressed in percentage of the observed values.

The index of agreement between estimates of the model chosen and the values of leaf area observed was carried out using index (d) (Willmott et al., 1985). The values found ranged from "zero" (without agreement) to "one" (perfect agreement). From this perspective, the closer to the unit, the more accurate will be the model to estimate the leaf area. The (d) value is calculated using the following equation:

where d = Willmott's index of agreement; LA_est = leaf area estimated by the regression model chosen; LA_obs = leaf area observed and = general average of leaf areas observed (Fialho et al., 2011).

The statistical analyses were carried out using the software "SigmaPlot" (Jandel Scientific, 1986), "Table Curve 2D v 5.0 trial" (Jandel Scientific, 1991) and "Genes" - computer application in genetics and statistics v. 2015.5.0 (Cruz, 2013).

RESULTS AND DISCUSSION

For the nondestructive determination of yacon leaf area, several linear and nonlinear models were fitted between length (L), width (W) and leaf area observed (LA_obs ) (data not shown).

However, six linear models are presented, considering that these models best satisfied the pre-established statistics. Thus, the authors decided to compare these models, choosing among them the best one, statistically. Two of them involving separately (L and W), two involving sum {L+W; (L+W)/2} and two involving the product {LW; (LW)/2}; (Table 1).

1length (comprimento) (L); width (largura) (W); **Coefficients (coeficientes) - significant through t-test (significativo pelo teste-t) (α= 0.01); **F calc - significant through F test (significativo pelo teste F) (α= 0.01).

• 1length (comprimento) (L); width (largura) (W); **Coefficients (coeficientes) - significant through t-test (significativo pelo teste-t) (α= 0.01); **F calc - significant through F test (significativo pelo teste F) (α= 0.01).

The coefficient of determination adjusted for the degrees of freedom of the models tested were: 95.72%, 95.71%, 95.38%, 95.38%, 93.23% and 90.99% for the models, LA_LW, LA_LW/2 , LA_L+W , LA_L+W/2 , LA_L and LA_W respectively (Table 1). Thus, the models which use the product LW to predict the yacon leaf area are more accurate (higher R_a ² and lower SE).

Similar notes were taken by Strik & Proctor (1985) which also concluded that the joint use of length and width best estimated the strawberry leaflet area, and by Lu et al. (2004), when they worked with taro cultivars. On the other hand, Aquino et al. (2011) observed that length × width, as well as only width would be adequate to estimate the sunflower leaf blade area, a species belonging to the yacon family, with similar morphological leaves. Also for sunflower, Maldaner et al. (2009) observed that the use of only width, with the power-type model, presents considerable accuracy to estimate the leaf area.

The authors highlight that in LA_LW and LA_LW/2, the reduction of error of estimates (lower SE) was manifested through the increasing F_calc and the decreasing residual sum of squares (R-SS) compared with the other models (Table 1), emphasizing that LA_LW and LA_LW/2 were more efficient, based on the selection criteria proposed by Antunes et al. (2008).

In yacon potato, regression analysis showed that most of the variation in leaf area values was explained through length (L) x width (W) variables, even dividing this value by half (LA_LW/2 ). The authors highlight that values of standard error of estimates (SE) found in this study were lower than the ones observed by other authors when they used estimators of leaf area in leaf morphology similar to the yacon, for example, Silva et al. (1998), working with pumpkin; Nascimento et al. (2002), working with melon; and by Fialho et al. (2011), working with zucchini.

In relation to the residuals distribution pattern along the independent variables of the models contrasted (Figure 2A, B, C, D, E and F), the authors also noticed that the best pattern was also obtained for the models with values of leaf area estimated through the product of leaf length and width (LA_LW and LA_LW/2 ) (Figure 2C and D), where the authors noticed a more uniform residual distribution and thus, tendency to normal distribution and to homogeneity of residual variance.

Figure 2
Dispersion pattern of errors analysis for the respective polynomial models. A: Length (C); B: width (L) and; C: (C*L); D: product (C*L)/2; E: (C+L); F: (C+L)/2 (análise de dispersão padrão dos resíduos para os respectivos modelos polinomiais A: comprimento (C); B: largura (L) e; C: produto (C*L); D: produto (C*L)/2; E: soma (C+L); F: soma (C+L)/2. Alegre-ES, UFES, 2014.

Thus, to be simpler and show only the product between the variables (length - L and width - W), lower SE, higher R_a ², significant parameters of regression and a normal distribution pattern of residuals, the model chosen was: LA_LW , logarithm (Table 1), having as estimator: LA_LW = (-27.7418 + (3.9812LW / ln LW ) .

On the other hand, Lima et al. (2008) defined potential and linear equations for estimating the leaf area in cowpea beans. In a similar way, for sunflower crop, power model was chosen for being the most accurate (Maldaner et al., 2009).

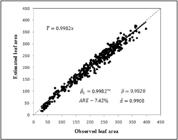
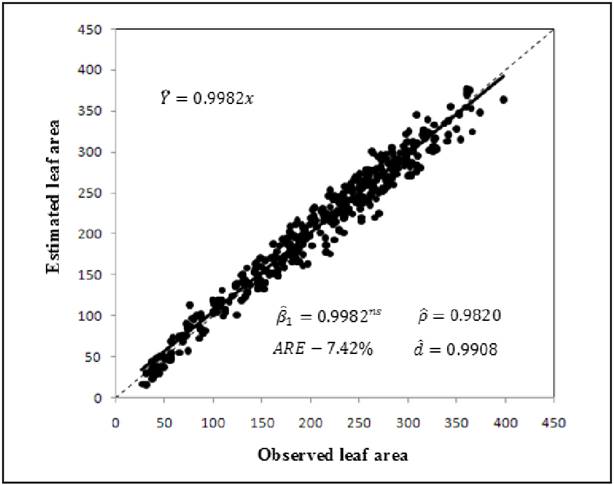
Validation showed that the logarithmic model chosen is very precise and accurate, considering that in LRMWI did not differ from the unit by the Student's t-test (α = 0.01). Where:

The authors also noticed strong linear dependence between the data observed and estimated by the model mentioned, Pearson correlation ̂p = 0.982, which in magnitude was close to the unit and data showed the same variation (Figure 3). Average relative error expressed in percentage of the data observed was 7%, considerably small, reinforcing the accuracy of the model chosen.

Figure 3
Ratio between observed and estimated leaf area using the logarithmic model ((LALW = (-27.7418 + (3.9812LW / ln LW )) based on the product of length (L) and width (W) of yacon leaves (see Table 1) (relação entre área foliar observada e estimada usando o modelo logarítmico (AFCL = (-27,7418 + (3,9812CL / ln CL), baseado no produto do comprimento (C) pela largura (L) da folha de batata yacon) (vide Tabela 1); *Some items were inserted into the Figure: results of the statistics used for validating the model t-test for β under the assumption H0: β =1 vs. H0: β ≠1 (α=0.01); Pearson's correlation coefficient ( ̂p = 0,9820) average relative error in percentage of observed values (ARE%) and Willmott's concordance index (d). **The dotted line is the equivalence line 1:1 ns - non-significant by Student's t-test (α=0.01) (encontram-se inseridas na figura os resultados das estatísticas utilizadas na validação do modelo: teste-t para o β sob a hipótese H0: β =1 vs. H0: β ≠1 (α=0,01); coeficiente de correlação de Pearson (̂p = 0,9820 ); erro relativo médio em porcentagem dos valores observados (ERM%) e índice de concordância de Willmott (d). **A linha pontilhada é a reta de equivalência 1:1 ns - não significativo pelo teste-t de Student (α=0,01).

The Willmott's index (d) showed clear concordance between data observed and estimated ̂d = 0.9908, reaffirming the results of the statistics previously carried out for the model tested (Figure 3).

The estimator LA_LW = (-27.7418 + (3.9812LW / ln LW) chosen proved to be the right choice, due to the results obtained during validation. The small average relative error (ARE%) of 7% observed can be explained by the large variability in size and shape of the leaves used. All the criteria evaluated during the validation indicate that the model chosen show good adjustment and high reliability.

Thus, this work proves that the nondestructive leaf area estimation in yacon potato can be carried out based on leaf length (L) and width (W), independent on size, through the estimator LA_LW = (-27.7418 + (3.9812LW / ln LW).

ACKNOWLEDGEMENT

To CNPq and FAPES for financial support and to FAPES for the 2nd author research grant.

REFERENCES

• ANTUNES, WC; POMPELLI, MF; CARRETERO, DM; MATTA, FM. 2008. Allometric models for non-destructive leaf area estimation in coffee (Coffea arabica and C. canephora). Annals of Applied Biology 153: 33-40.
• AQUINO, LA; SANTOS JUNIOR, VC; GUERRA, JVS; COSTA, MM. 2011. Estimativa da área foliar do girassol por método não destrutivo. Bragantia 70: 832-836.
• BLANCO, FF; FOLEGATTI, MV. 2005. Estimation of leaf area for greenhouse cucumber by linear measurements under salinity and grafting. Scientia Agrícola 62: 305-309.
• Cruz, CD. 2013. GENES: a software package for analysis in experimental statistics and quantitative genetics. Acta Scientiarum 35: 271-276.
• FAVARIN, JL; DOURADO NETO, D; GARCÍA, Y; GARCÍA, A; VILLA NOVA, NA; FAVARIN, MGGV. 2002. Equações para a estimativa do índice de área foliar do cafeeiro. Pesquisa Agropecuária Brasileira 37: 769-773.
• FIALHO, GS; DALVI, LP; DALVI, NBC; KUHLCAMP, TK; EFFGEN, EM. 2011. Predição da área foliar em abobrinha-italiana: um método não destrutivo, exato, simples, rápido e prático. Revista Brasileira de Agropecuária Sustentável 1: 59-63.
• INMET - INMET - INSTITUTO NACIONAL DE METEOROLOGIA. 2014. Disponível em Disponível em http://www.inmet.gov.br Acessado em 07 de agosto de 2014.
  » http://www.inmet.gov.br
• LIMA, CJGS; OLIVEIRA, FA; MEDEIROS, JF; OLIVEIRA, MKT; OLIVEIRA FILHO, AF. 2008. Modelos matemáticos para estimativa de área foliar em feijão caupi. Revista Caatinga 21: 120-127.
• LU, HY; LU, CT; WEI, ML; CHAN, LF. 2004. Comparison of different models for nondestructive leaf area estimation in taro. Agronomy Journal 96: 448-453.
• MANRIQUE, I; PÁRRAGA, A. 2005. Conservación y uso de la biodiversidad de raíces y tubérculos Andinos: Uma década de investigación para el desarrollo (1993-2003)Jarabe de yacón: principios y procesamiento. Lima: Centro Internacional de La Papa. 40p.
• MOSCATTO, JA; PRUDÊNCIO, SH; HAULY, MCO. 2004. Farinha de yacon e inulina como ingredientes na formulação de bolo de chocolate. Ciência e Tecnologia de Alimentos 24: 634-40.
• MALDANER, IC; HELDWEIN, BA; LOOSE, LH; LUCAS, DDP; GUSEL, FI; BORTOLUZZI, MP. 2009. Modelos de determinação não-destrutiva da área foliar em girassolCiência Rural 39: 1356-1361.
• NASCIMENTO, IB; FARIAS, CHA; SILVA, MCC; MEDEIROS, JF; ESPÍNOLA SOBRINHO, J; NEGREIROS, MZ. 2002. Estimativa da área foliar do meloeiro. Horticultura Brasileira 20: 555-558.
• POMPELLI, MF; ANTUNES, WC; FERREIRA, DTRG; CAVALCANTE, PGS; WANDERLEY-FILHO, HCL; ENDRES, L. 2012. Allometric models for non-destructive leaf area estimation of Jatropha curcas Biomass & Bioenergy 36: 77-85.
• SANTANA, I; CARDOSO, MH. 2008. Raiz tuberosa de yacon (Smallanthus sonchifolius): potencialidade de cultivo, aspectos tecnológicos e nutricionais. Ciência Rural 38: 898-905.
• SEMINARIO, J; VALDERRAMA, M; MANRIQUE, I. 2003. El yacon: fundamentos 'para el aprovechamiento de un recurso promisorio. Lima: Centro Internacional de La Papa (CIP), Universidad Nacional de Cajamarca, Agencia Suiza para el Desarrollo y la Cooperación (COSUDE). 60p. Online. Disponível em: Disponível em: http://www.cipotato.org/market/PDFdocs/Yacon_Fundamentos_password.pdf Acessado em 18 de junho de 2012.
  » http://www.cipotato.org/market/PDFdocs/Yacon_Fundamentos_password.pdf
• SILVA, WZ; BRINATE, SVB; TOMAZ, MA; AMARAL, JFT; RODRIGUES, WN; MARTINS, LD. 2011. Métodos de estimativa de área foliar em cafeeiro. Enciclopédia Biosfera 7: 746-759.
• SILVA, NF; FERREIRA, FA; FONTES, PCR; CARDOSO, AA. 1998. Modelos para estimar a área foliar de abóbora por meio de medidas lineares. Revista Ceres 45: 287-291.
• STRIK, BC; PROCTOR, JTA. 1985. Estimating the area of trifoliate and unequally imparipinnate leaves of strawberry. HortScience 20: 1072-1074.
• VILHENA, SMC; CÂMARA, FL; KADIHARA, ST. 2000. O cultivo do yacon no Brasil. Horticultura Brasileira 18: 5-8.
• WILLMOTT, CJ. et al. 1985. Statistics for the evaluation and comparisons of models. Journal of Geophysical Research 90: 8995-9005.

Publication Dates

• Publication in this collection
  Jul-Sep 2016

History

• Received
  27 Apr 2015
• Accepted
  05 Mar 2016